Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s0.4

Concluding Comments

The conservation laws as applied to collisions of monatomic molecules can be ob-

tained from the results above as follows: Eqs. 0.3-1, 0.3-2, and 0.3-4 are directly applica-

ble; Eq. 0.3-6 is applicable if the internal energy contributions are omitted; and

Eq.

0.3-8

may be used if the internal angular momentum terms are discarded.

Much of this book will be concerned with setting up the conservation laws at the mi-

croscopic and macroscopic levels and applying them to problems of interest in engineer-

ing

and science. The above discussion should provide a good background for this

adventure. For a glimpse of the conservation laws for species mass, momentum, and en-

ergy at the microscopic and macroscopic levels, see Tables 19.2-1 and 23.5-1.

50.4

CONCLUDING COMMENTS

To use the macroscopic balances intelligently, it is necessary to use information about in-

terphase transport that comes from the equations of change. To use the equations of

change, we need the transport properties, which are described by various molecular the-

ories. Therefore, from a teaching point of view, it seems best to start at the molecular

level and work upward toward the larger systems.

All the discussions of theory are accompanied by examples to illustrate how the the-

ory is applied to problem solving, Then at the end of each chapter there are problems to

provide extra experience in using the ideas given in the chapter. The problems are

grouped into four classes:

Class A: Numerical problems, which are designed to highlight important equa-

tions in the text and to give a feeling for the orders of magnitude.

Class

Analytical problems that require doing elementary derivations using

ideas mainly from the chapter.

Class

More advanced analytical problems that may bring ideas from other chap-

ters or from other books.

Class

Problems in which intermediate mathematical skills are required.

Many of the problems and illustrative examples are rather elementary in that they in-

volve oversimplified systems or very idealized models. It is, however, necessary to start

with these elementary problems in order to understand how the theory works and to de-

velop confidence in using it. In addition, some of these elementary examples can be very

useful in making order-of-magnitude estimates in complex problems.

Here are a few suggestions for studying the subject of transport phenomena:

Always read the text with pencil and paper in hand; work through the details of

the mathematical developments and supply any missing steps.

Whenever necessary, go back to the mathematics textbooks to brush up on calculus,

differential equations, vectors, etc. This is an excellent time to review the mathemat-

ics that was learned earlier (but possibly not as carefully as it should have been).

Make it a point to give

physical interpretation of key results; that is, get in the

habit of relating the physical ideas to the equations.

Always ask whether the results seem reasonable. If the results do not agree with

intuition, it is important to find out which is incorrect.

Make it a habit to check the dimensions of all results. This is one very good way of

locating errors in derivations.

We hope that the reader will share our enthusiasm for the subject of transport phe-

nomena. It will take some effort to learn the material, but the rewards will be worth the

time and energy required.

Chapter

The Subject of Transport Phenomena

QUESTIONS FOR DISCUSSION

What are the definitions of momentum, angular momentum, and kinetic energy for a single

particle? What are the dimensions of these quantities?

What are the dimensions of velocity, angular velocity, pressure, density, force, work, and

torque? What are some common units used for these quantities?

Verify that it is possible to go from

Eq.

0.3-3

Eq.

0.3-4.

Go through all the details needed to get Eq.

0.3-6

from

Eq.

0.3-5.

Suppose that the origin of coordinates

shifted to a new position. What effect would that

have on

Eq.

0.3-7?

the equation changed?

Compare and contrast angular velocity and angular momentum.

What is meant by internal energy? Potential energy?

Is the law of conservation of mass always valid? What are the limitations?

Part

One

Momentum

Transport

This Page Intentionally Left Blank

Chapter

Viscosity and the Mechanisms

of Momentum Transport

51.1

Newton's law of viscosity (molecular momentum transport)

Generalization of Newton's law of viscosity

1.3

Pressure and temperature dependence of viscosity

~1.4'

Molecular theory of the viscosity of gases at low density

51.5'

Molecular theory of the viscosity of liquids

51.6'

Viscosity of suspensions and emulsions

1.7

Convective momentum transport

The first part of this book deals with the flow of viscous fluids. For fluids of low molecu-

lar weight, the physical property that characterizes the resistance to flow is the

viscosity.

Anyone who has bought motor oil is aware of the fact that some oils are more "viscous"

than others and that viscosity is a function of the temperature.

We begin in 31.1 with the simple shear flow between parallel plates and discuss how

momentum is transferred through the fluid by viscous action. This is an elementary ex-

ample of

molecular momentum transport

and it serves to introduce "Newton's law of vis-

cosity" along with the definition of viscosity

Next in 31.2 we show how Newton's law

can be generalized for arbitrary flow patterns. The effects of temperature and pressure

on the viscosities of gases and liquids are summarized in 51.3 by means of a dimension-

less plot. Then 51.4 tells how the viscosities of gases can be calculated from the kinetic

theory of gases, and in 51.5 a similar discussion is given for liquids. In

51.6

we make a

few comments about the viscosity of suspensions and emulsions.

Finally, we show in 31.7 that momentum can also be transferred by the bulk fluid

motion and that such

convective momentum transport

is proportional to the fluid density

51.1

NEWTON'S LAW OF VISCOSITY (MOLECULAR

TRANSPORT OF MOMENTUM)

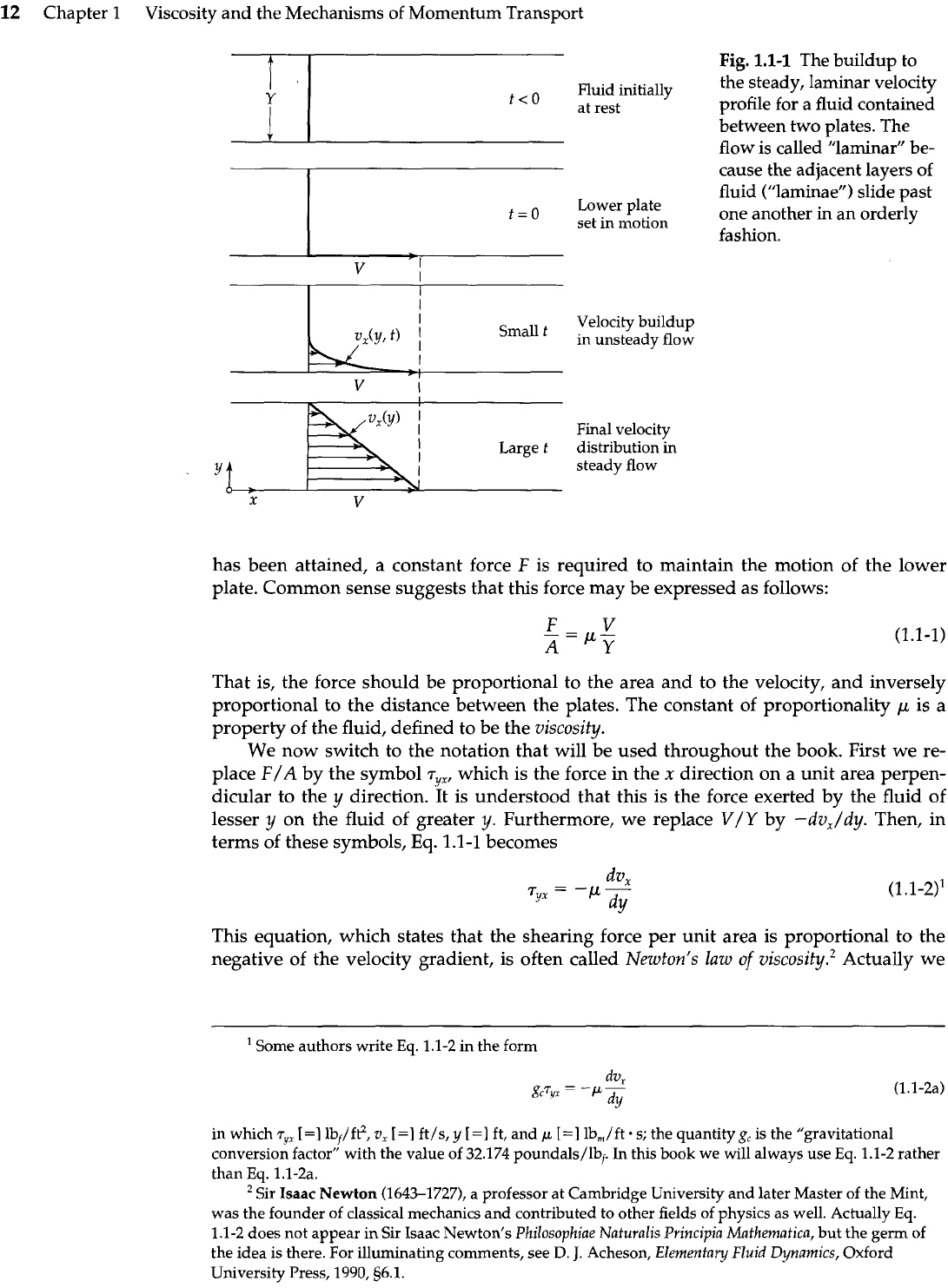
In Fig.

1.1-1

we show a pair of large parallel plates, each one with area

separated by a

distance

In the space between them is a fluid-either a gas or a liquid. This system is

initially at rest, but at time

the lower plate is set in motion in the positive

direc-

tion at a constant velocity

As time proceeds, the fluid gains momentum, and ulti-

mately the linear steady-state velocity profile shown in the figure is established. We

require that the flow be laminar ("laminar" flow is the orderly type of flow that one usu-

ally observes when syrup is poured, in contrast to "turbulent" flow, which is the irregu-

lar, chaotic flow one sees in a high-speed mixer). When the final state of steady motion

Chapter

Viscosity and the Mechanisms of Momentum Transport

Fluid initially

at rest

Lower plate

set in motion

Velocity buildup

in unsteady flow

Fig.

1.1-1

The buildup to

the steady, laminar velocity

profile for a fluid contained

between two plates. The

flow is called "laminar" be-

cause the adjacent layers of

fluid ("laminae") slide past

one another in an orderly

fashion.

Final velocity

Large

distribution in

steady flow

has been attained,

constant force

is required to maintain the motion of the lower

plate. Common sense suggests that this force may be expressed as follows:

That is, the force should be proportional to the area and to the velocity, and inversely

proportional

the distance between the plates. The constant of proportionality

is a

property of the fluid, defined to be the

viscosity.

We now switch to the notation that will be used throughout the book. First we re-

place

F/A

the symbol

T,,,

which is the force in the

direction on a unit area perpen-

dicular to the

direction. It is understood that this is the force exerted by the fluid of

lesser

on the fluid of greater

Furthermore, we replace

V/Y

-dvx/dy.

Then, in

terms of these symbols,

Eq.

1.1-1 becomes

This equation, which states that the shearing force per unit area is proportional to the

negative of the velocity gradient, is often called

Newton's

law

visco~ity.~

Actually we

Some authors write Eq.

1.1-2

in the form

in which

ryx

[=]

lbf/ft2,

[=]

ft/s,

[=I

ft, and

[=]

lb,/ft. s; the quantityg, is the "gravitational

conversion factor" with the value of

32.174

poundals/lbf.

this book we will always use

Eq.

1.1-2

rather

than Eq.

1.1-2a.

Sir

Isaac

Newton

(1643-1727),

a professor at Cambridge University and later Master of the Mint,

was the founder of classical mechanics and contributed to other fields of physics as well. Actually Eq.

1.1-2

does not appear in Sir Isaac Newton's

Philosophiae Naturalis Principia

Mathematics,

but the germ of

the idea is there. For illuminating comments, see

Acheson,

Elementary

Fluid Dynamics,

Oxford

University Press,

1990,§6.1.

51.1

Newton's Law of Viscosity (Molecular Transport of Momentum)

should not refer to Eq. 1.1-2 as a "law," since Newton suggested it as an empiricism3-

the simplest proposal that could be made for relating the stress and the velocity gradi-

ent. However, it has been found that the resistance to flow of all gases and all liquids

with molecular weight of less than about 5000 is described by Eq. 1.1-2, and such fluids

are referred to as Newtonian fluids. Polymeric liquids, suspensions, pastes, slurries, and

other complex fluids are not described by

Eq.

1.1-2 and are referred to as non-Newtonian

fluids.

Polymeric liquids are discussed in Chapter

Equation 1.1-2 may be interpreted in another fashion. In the neighborhood of the

moving solid surface at

the fluid acquires a certain amount of x-momentum. This

fluid, in turn, imparts momentum to the adjacent layer of liquid, causing it to remain in

motion in the

direction. Hence x-momentum is being transmitted through the fluid in

the positive

direction. Therefore

r,,

may also be interpreted as the flux

x-momentum

in the positive

direction, where the term "flux" means "flow per unit area." This interpre-

tation is consistent with the molecular picture of momentum transport and the kinetic

theories of gases and liquids. It also is in harmony with the analogous treatment given

later for heat and mass transport.

The idea in the preceding paragraph may be paraphrased by saying that momentum

goes "downhill" from a region of high velocity to a region of low velocity-just as a sled

goes downhill from a region of high elevation to a region of low elevation, or the way

heat flows from a region of high temperature to a region of low temperature. The veloc-

ity gradient can therefore be thought of as

"driving force" for momentum transport.

In what follows we shall sometimes refer to Newton's law in Eq. 1.1-2 in terms of

forces (which emphasizes the mechanical nature of the subject) and sometimes in terms

of momentum transport (which emphasizes the analogies with heat and mass transport).

This dual viewpoint should prove helpful in physical interpretations.

Often fluid dynamicists use the symbol

to represent the viscosity divided by the

density (mass per unit volume) of the fluid, thus:

This quantity is called the kinematic viscosity.

Next we make a few comments about the units of the quantities we have defined. If

we use the symbol

[=I

to mean "has units of," then in the SI system

r,,

[=I

N/m2

Pa,

m/s, and

[=I

m, so that

since the units on both sides of Eq. 1.1-2 must agree. We summarize the above and also

give the units for the c.g.s. system and the British system in Table 1.1-1. The conversion

tables in Appendix

will prove to be very useful for solving numerical problems involv-

ing diverse systems of units.

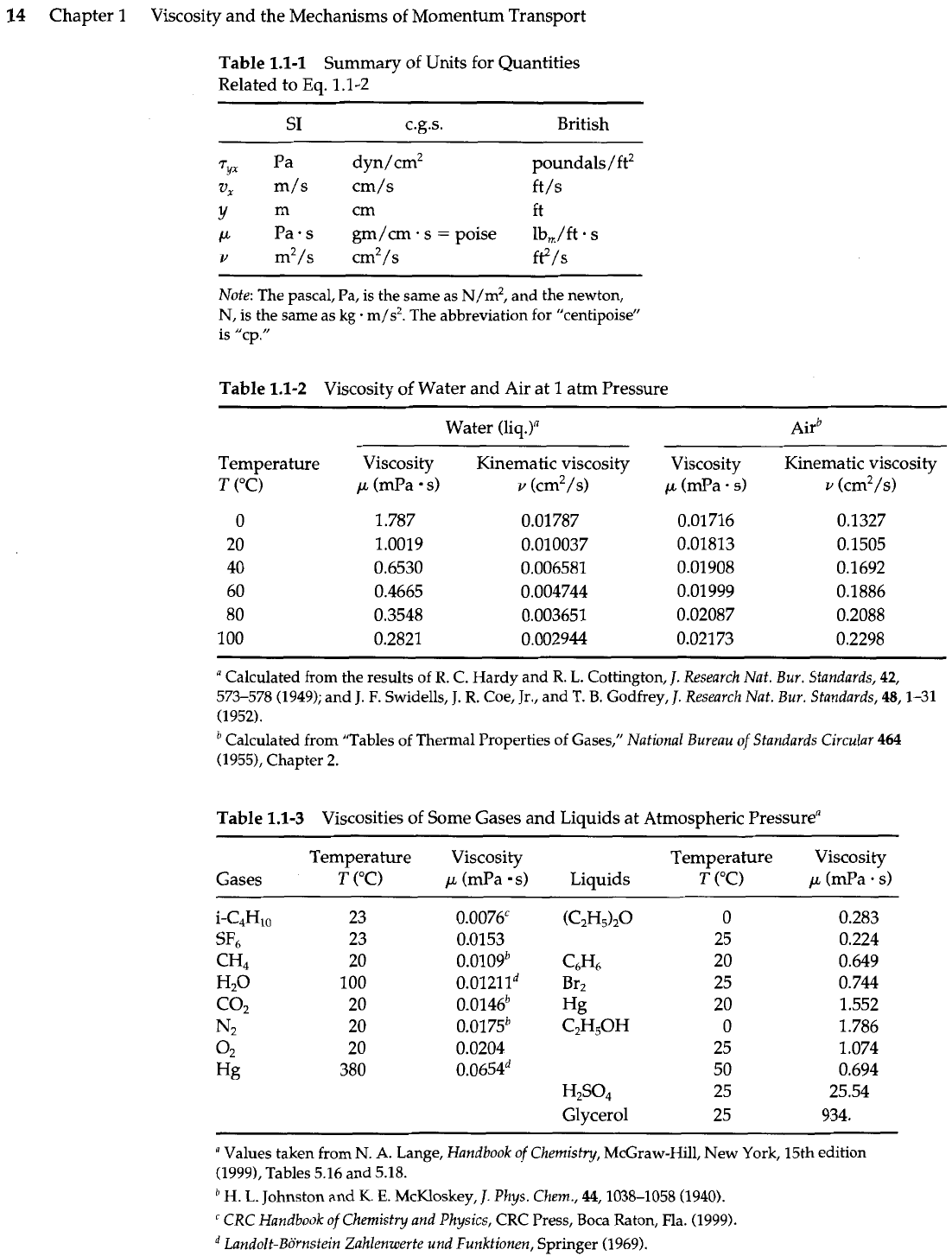
The viscosities of fluids vary over many orders of magnitude, with the viscosity of

air at 20°C being

1.8

s and that of glycerol being about

s, with some sili-

cone oils being even more viscous. In Tables 1.1-2,l. 1-3, and 1.1-4 experimental data4 are

A relation of the form of Eq. 1.1-2 does come out of the simple kinetic theory of gases (Eq. 1.4-7).

However, a rigorous theory for gases sketched in Appendix

makes it clear that Eq. 1.1-2 arises as the

first term in an expansion, and that additional (higher-order) terms are to

expected. Also, even an

elementary kinetic theory of liquids predicts non-Newtonian behavior (Eq. 1.5-6).

comprehensive presentation of experimental techniques for measuring transport properties can be

found in W. A. Wakeham,

Nagashima, and

Sengers,

Measurement of the Transporf Properties offluids,

CRC Press, Boca Raton,

Fla.

(1991). Sources for experimental data are: Landolt-Bornstein,

Zahlenwerte und

Funktionen,

Vol. II,5, Springer (1968-1969);

International Critical Tables,

McGraw-Hill, New York (1926);

S. Touloukian,

E. Liley, and S. C. Saxena,

Tkermopkysical Properties of Matter,

Plenum Press, New York

(1970); and also numerous handbooks of chemistry, physics, fluid dynamics, and heat transfer.

Chapter

Viscosity and the Mechanisms of Momentum Transport

Table

1.1-1

Summary of Units for Quantities

Related to Eq.

1 .l-2

SI c.g.s. British

Note:

The pascal, Pa, is the same as N/m2, and the newton,

is the same as kg

m/s2. The abbreviation for "centipoise"

is "cp."

Table

1.1-2

Viscosity of Water and Air at

atm Pressure

Water (liq.)"

Temperature

("C)

Viscosity

(mPa s)

1.787

1.0019

0.6530

0.4665

0.3548

0.2821

Kinematic viscosity

(cm2/s)

0.01 787

0.010037

0.006581

0.004744

0.003651

0.002944

Viscosity

(mPa. s)

Kinematic viscosity

(cm2/s)

Talculated from the results of

C. Hardy and

Cottington,

Research Nut. Bur. Standards,

42,

573-578 (1949); and

Swidells, J. R. Coe, Jr., and T.

Godfrey,

Research Naf. Bur. Standards,

48,l-31

(1952).

Calculated from "Tables

Thermal Properties of Gases,"

National Bureau of Standards Circular

464

(1955), Chapter

Table

1.1-3

Viscosities of Some Gases and Liquids at Atmospheric Pressurea

Temperature Viscosity Temperature Viscosity

Gases

CC)

(mPa s) Liquids

rC)

(mPa. s)

(C&&,O

C6H6

Br2

C2H50H

H2S0,

Glycerol

Talues taken from N.

Lange,

Handbook of Chemistry,

McGraw-Hill, New York, 15th edition

(1999), Tables 5.16 and 5.18.

Johnston

and

McKloskey,

Phys.

Chern.,

44,1038-1058 (1940).

CRC Handbook of Chemistry and Physics,

CRC Press, Boca Raton,

Fla.

(1999).

Landolt-Bornstein Zahlenwerfe und Funktionen,

Springer (1969).

$1.1 Newton's Law of Viscosity (Molecular Transport of Momentum)

Table

1.1-4

Viscosities of Some Liquid Metals

Temperature Viscosity

Metal

("(3

(mPa s)

Data taken from

The Reactor Handbook,

Vol.

Atomic

Energy Commission

AECD-3646,

U.S.

Government

Printing

Office,

Washington, D.C. (May

1955),

pp.

258

et seq.

given for pure fluids at

atm pressure. Note that for gases at low density, the viscosity

increases

with increasing temperature, whereas for liquids the viscosity usually

decreases

with increasing temperature. In gases the momentum is transported by the molecules in

free flight between collisions, but in liquids the transport takes place predominantly by

virtue of the intermoIecular forces that pairs of molecules experience as they wind their

way around among their neighbors. In

g51.4

and

1.5

we give some elementary kinetic

theory arguments to explain the temperature dependence of viscosity.

Compute the steady-state momentum flux

T,,

in lbf/ft? when the lower plate velocity

in Fig.

1.1-1 is I ft/s in the positive

direction, the plate separation

is 0.001 ft, and the fluid viscos-

Calculation of

ity

is 0.7 cp.

Momentum Flux

SOLUTION

Since

T~,

is desired in British units, we should convert the viscosity into that system of units.

Thus, making use of Appendix

we find

(0.7 cp)(2.0886

1.46

Ibf

s/ft2.

The velocity profile is linear so that

dv,

Av,

-1.0 ft/s

-10oos-~

0.001 ft

Substitution into

Eq.

1.1-2 gives

Chapter 1 Viscosity and the Mechanisms of Momentum Transport

1.2

GENERALIZATION OF NEWTON'S LAW

VISCOSITY

In the previous section the viscosity was defined by

Eq.

1.1-2, in terms of a simple

steady-state shearing flow in which

is a function of

alone, and

and

are zero.

Usually we are interested in more complicated flows in which the three velocity compo-

nents may depend on all three coordinates and possibly on time. Therefore we must

have an expression more general than Eq. 1.1-2, but it must simplify to Eq. 1.1-2 for

steady-state shearing flow.

This generalization is not simple;

fact, it took mathematicians about a century and a

half to do this. It is not appropriate for us to give all the details of this development here,

since they can be found in many fluid dynamics books.' Instead we explain briefly the main

ideas that led to the discovery of the required generalization of Newton's law of viscosity.

To do this we consider a very general flow pattern, in which the fluid velocity may

in various directions at various places and may depend on the time

The velocity

components are then given by

In such

situation, there will be nine stress components

ril

(where

and

may take on

the designations

y, and

z),

instead of the component

that appears in

Eq.

1.1-2.

therefore must begin by defining these stress components.

Fig.

1.2-1 is shown a small cube-shaped volume element within the flow field,

each face having unit area. The center of the volume element is at the position x,

Fig.

1.2-1

Pressure and viscous forces acting on planes in the fluid perpendicular to the three

coordinate systems. The shaded planes have unit area.

Prager,

Introduction to Mechanics of Continua,

Ginn, Boston (1961),

pp.

89-91;

Aris,

Vectors,

Tensors, and the Basic Equations of Fluid Mechanics,

Prentice-Hall, Englewood Cliffs,

N.J.

(19621,

pp.

30-34,

99-112; L. Landau and

Lifshitz,

Fluid Mechanics,

Pergamon, London, 2nd edition (1987),

pp.

44-45.

Lev Davydovich Landau

(1908-1968) received the Nobel prize in 1962 for his work on liquid helium and

superfluid dynamics.