Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

52.5 Flow

Two Adjacent Immiscible Fluids

We may immediately make use of one of the boundary conditions-namely, that the

momentum flux

T,,

is continuous through the fluid-fluid interface:

B.C. 1: at

7',

(2.5-4)

This tells us that

Cil;

hence we drop the superscript and call both integration con-

stants

C,.

When Newton's law of viscosity is substituted into Eqs. 2.5-2 and 2.5-3, we get

These two equations can be integrated to give

The three integration constants can be determined from the following no-slip boundary

conditions:

B.C.

atx

.i'

(2.5-9)

B.C. 3: atx

-b,

(2.5-10)

B.C. 4: atx

+b,

(2.5-11)

When these three boundary conditions are applied, we get three simultaneous equations

for the integration constants:

from B.C.

(2.5-12)

from B.C.

from B.C. 4:

From these three equations we get

The resulting momentum-flux and velocity profiles are

'pa

;pJb

[((X

(

)]

(

(2.5-17)

Chapter 2 Shell Momentum Balances and Velocity Distributions in Laminar Flow

These distributions are shown in Fig. 2.5-1. If both viscosities are the same, then the ve-

locity distribution is parabolic, as one would expect for a pure fluid flowing between

parallel plates (see Eq. 2B.3-2).

The average velocity in each layer can be obtained and the results are

From the velocity and momentum-flux distributions given above, one can also calculate

the maximum velocity, the velocity at the interface, the plane of zero shear stress, and

the drag on the walls of the slit.

52.6

CREEPING

FLOW AROUND A

SPHERE^^^^^^^

In the preceding sections several elementary viscous flow problems have been solved.

These have all dealt with rectilinear flows with only one nonvanishing velocity compo-

nent. Since the flow around a sphere involves two nonvanishing velocity components,

and v,, it cannot be conveniently understood by the techniques explained at the begin-

ning of this chapter. Nonetheless, a brief discussion of flow around a sphere is warranted

here because of the importance of flow around submerged objects. In Chapter 4 we show

how to obtain the velocity and pressure distributions. Here we only cite the results and

show how they can be used to derive some important relations that we need in later dis-

cussions. The problem treated here, and also in Chapter 4, is concerned with "creeping

flowu-that is, very slow flow. This type of flow is also referred to as "Stokes flow."

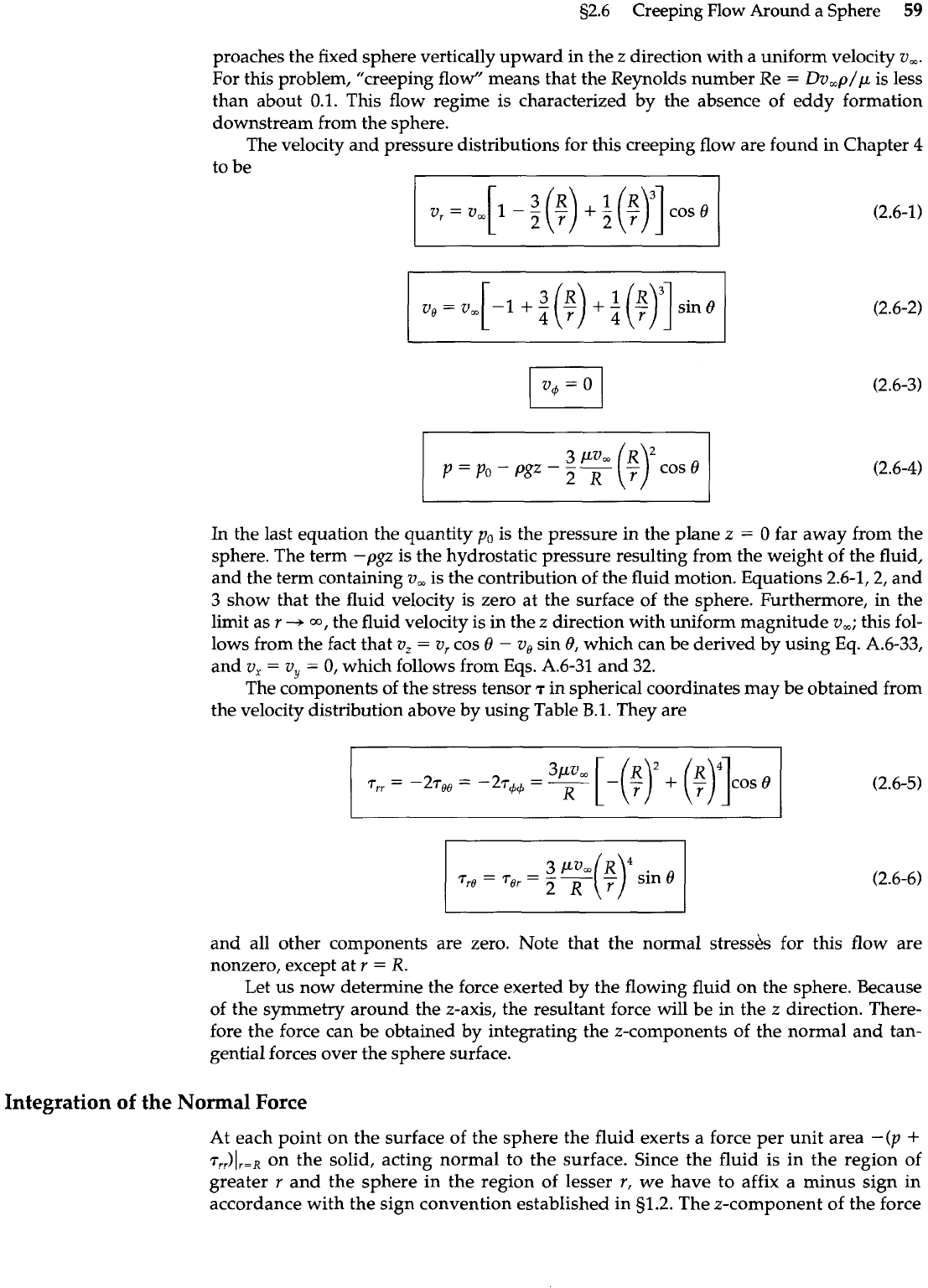
We consider here the flow of an incompressible fluid about a solid sphere of radius

and diameter

as shown in Fig. 2.6-1. The fluid, with density

and viscosity p, ap-

Radius of sphere

At every point there are

pressure and friction

forces acting on the

Fluid approaches

from below with

velocity

Point in space

(x,

z) or

(r,

0,4)

Projection

of point on

xy-plane

Fig.

2.6-1

Sphere of radius

around which a fluid is flow-

ing. The coordinates r,

and

are shown. For more informa-

tion on spherical coordinates,

see Fig. A.8-2.

Stokes,

Trans. Cambridge Phil. Soc.,

9,8-106 (1851). For creeping flow around an object of

arbitrary shape, see

Brenner,

Chem. Engr. Sci.,

19,703-727 (1964).

Landau and

Lifshitz,

Fluid Mechanics,

2nd edition, Pergamon, London (1987), §20.

Batchelor,

An Introduction to Fluid Dynamics,

Cambridge University Press (1967), s4.9.

S. Kim and

Karrila,

Microhydrodynamics: Principles and Selected Applications,

Butterworth-

Heinemann, Boston (1991),

s4.2.3;

this book contains a thorough discussion of "creeping flow" problems.

92.6

Creeping Flow Around a Sphere

proaches the fixed sphere vertically upward in the

direction with a uniform velocity

v,.

For this problem, "creeping flow" means that the Reynolds number Re

Dv,p/p

is less

than about 0.1. This flow regime is characterized by the absence of eddy formation

downstream from the sphere.

The velocity and pressure distributions for this creeping flow are found in Chapter

to be

=..[-I

t(:)

++(:I

sin,

=pa

pgz

2 R

cos

In the last equation the quantity

is the pressure in the plane z

far away from the

sphere. The term

-pgz

is the hydrostatic pressure resulting from the weight of the fluid,

and the term containing

is the contribution of the fluid motion. Equations 2.6-1,2, and

3 show that the fluid velocity is zero at the surface of the sphere. Furthermore, in the

limit as

the fluid velocity is in the

direction with uniform magnitude

v,;

this fol-

lows from the fact that

cos 8

sin 8, which can be derived by using Eq. A.6-33,

and

0, which follows from Eqs. A.6-31 and 32.

The components of the stress tensor

in spherical coordinates may be obtained from

the velocity distribution above by using Table

B.1.

They are

rrB

TBr

pvm(~)I

sin

and all other components are zero. Note that the normal stressks for this flow are

nonzero, except at

Let us now determine the force exerted by the flowing fluid on the sphere. Because

of the symmetry around the z-axis, the resultant force will be in the

direction. There-

fore the force can be obtained by integrating the z-components of the normal and tan-

gential forces over the sphere surface.

Integration of the Normal Force

At each point on the surface of the sphere the fluid exerts a force per unit area

-(p

T,,)[,=~

on the solid, acting normal to the surface. Since the fluid is in the region of

greater

and the sphere in the region of lesser

we have to affix a minus sign in

accordance with the sign convention established in 51.2. The z-component of the force

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

-(p

T,,)(,,~(cos

0). We now multiply this by a differential element of surface

sin 0 d0

to get the force on the surface element (see Fig. A.8-2). Then we inte-

grate over the surface of the sphere to get the resultant normal force in the

direction:

According to Eq. 2.6-5, the normal stress

is zero5 at

R and can be omitted in the in-

tegral in Eq. 2.6-7. The pressure distribution at the surface of the sphere is, according to

Eq. 2.6-4,

PVw

plr=R

pgR cos

cos

2 R

(2.6-8)

When this is substituted into Eq. 2.6-7 and the integration performed, the term contain-

ing p0 gives zero, the term containing the gravitational acceleration g gives the buoyant

force, and the term containing the approach velocity

gives the "form drag" as shown

below:

F'"'

$d3pg

2~,uRv,

(2.6-9)

The buoyant force is the mass

displaced fluid

(~TR~~)

times the gravitational accelera-

tion

(g).

Integration

the Tangential Force

At each point on the solid surface there is also a shear stress acting tangentially. The

force per unit area exerted in the

-0

direction by the fluid (region of greater r) on the

solid (region of lesser r) is +rY8~,=,. The 2-component of this force per unit area is

(T,&~)

sin 0. We now multiply this by the surface element

sin 0 d0d+ and integrate over the

entire spherical surface. This gives the resultant force in the

direction:

The shear stress distribution on the sphere surface, from Eq. 2.6-6, is

Substitution of this expression into the integral in Eq. 2.6-10 gives the "friction drag"

Hence the total force

of the fluid on the sphere is given by the sum of Eqs. 2.6-9 and

2.6-12:

$TR~~~

2~,uRv,

~T~Rv,

buoyant

form friction

force drag

drag

$rR3pg

6r,uRv,

buoyant kinetic

force force

Example

3.1-1

we show that, for incompressible, Newtonian fluids, all three of the normal

stresses are zero at fixed solid surfaces in all flows.

s2.6 Creeping Flow Around a Sphere

The first term is the

buoyant

force, which would be present in a fluid at rest; it is the mass

of the displaced fluid multiplied by the gravitational acceleration. The second term, the

kinetic force, results from the motion of the fluid. The relation

is known as Stokes'

law.'

It is used in describing the motion of colloidal particles under an

electric field, in the theory of sedimentation, and in the study of the motion of aerosol

particles. Stokes' law is useful only up to a Reynolds number Re

Dv,p/p

of about

0.1.

At Re

Stokes' law predicts a force that is about

10%

too low. The flow behavior for

larger Reynolds numbers

discussed in Chapter

This problem, which could not be solved by the shell balance method, emphasizes

the need for a more general method for coping with flow problems in which the stream-

lines are not rectilinear. That is the subject of the following chapter.

Derive a relation that enables one to get the viscosity of a fluid by measuring the terminal ve-

locity

of a small sphere of radius

in the fluid.

Determination of

Viscosity from the SOLUTION

Terminal Velocity

,fa

Falling

Sphere

If a small sphere is allowed to fall from rest in a viscous fluid, it will accelerate until it reaches

a constant velocity-the

terminal velocity.

When this steady-state condition has been reached

the sum of all the forces acting on the sphere must be zero. The force of gravity on the solid

acts

the direction of fall, and the buoyant and kinetic forces act in the opposite direction:

Here

and

are the densities of the solid sphere and the fluid. Solving this equation for the

terminal velocity gives

This result may be used only if the Reynolds number is less than about

0.1.

This experiment provides an apparently simple method for determining viscosity. How-

ever, it is difficult to keep a homogeneous sphere from rotating during its descent, and if it

does rotate, then Eq. 2.6-17 cannot be used. Sometimes weighted spheres are used in order to

preclude rotation; then the left side of Eq. 2.6-16 has to be replaced by

the mass of the

sphere, times the gravitational acceleration.

QUESTIONS FOR DISCUSSION

Summarize the procedure used in the solution of viscous flow

by the shell balance

method. What kinds of problems can and cannot be solved by this method? How is the defin-

ition of the first derivative used in the method?

Which of the flow systems in this chapter can be used as a viscometer? List the difficulties

that might be encountered in each.

How are the Reynolds numbers defined for films, tubes, and spheres? What are the dimen-

sions of Re?

How can one modify the film thickness formula in 52.2 to describe a thin film falling down

the interior wall of a cylinder? What restrictions might have to be placed on this modified for-

mula?

How can the results in

s2.3

used to estimate the time required for a liquid to drain out of

vertical tube that is open at both ends?

Contrast the radial dependence of the shear stress for the laminar flow of a Newtonian liquid

in a tube and

an annulus. In the latter, why does the function change sign?

Chapter 2 Shell Momentum Balances and Velocity Distributions in Laminar Flow

Show that the Hagen-Poiseuille formula is dimensionally consistent.

What differences are there between the flow in a circular tube of radius

and the flow in the

same tube with a thin wire placed along the axis?

Under what conditions would you expect the analysis in

s2.5

to be inapplicable?

Is Stokes' law valid for droplets of oil falling in water? For air bubbles rising in benzene? For

tiny particles falling in air, if the particle diameters are of the order of the mean free path of

the molecules in the air?

Two immiscible liquids,

and

are flowing in laminar flow between two parallel plates. Is

it possible that the velocity profiles would be of the following form? Explain.

12.

PROBLEMS

2A.1

2A.2

Liquid

What is the terminal velocity of a spherical colloidal particle having an electric charge

in an

electric field of strength

How is this used in the Millikan oil-drop experiment?

Thickness of a falling

film.

Water at 20°C

flowing down a vertical wall with Re

10.

Calculate (a) the flow rate, in gallons per hour per foot of wall width, and (b) the film thickness

in inches.

Answers:

(a) 0.727 gal/hr. ft; (b) 0.00361 in.

Determination of capillary radius by flow measurement. One method for determining the

radius of a capillary tube is by measuring the rate of flow of a Newtonian liquid through the

tube. Find the radius of a capillary from the following flow data:

Length of capillary tube 50.02 cm

Kinematic viscosity of liquid 4.03

m2/s

Density of liquid 0.9552

103 kg/m3

Pressure drop in the horizontal tube

4.829

lo5

Mass rate of flow through tube 2.997

kg/s

What difficulties may be encountered in this method? Suggest some other methods for deter-

mining the radii of capillary tubes.

Volume flow rate through an annulus. A horizontal annulus, 27

in length, has an inner ra-

dius of

0.495

in. and an outer radius of

1.1

in.

60% aqueous solution of sucrose (C,2H220,,)

is to be pumped through the annulus at 20°C. At this temperature the solution density is 80.3

lb/ft3 and the viscosity is 136.8 lb,/ft hr. What is the volume flow rate when the impressed

pressure difference is 5.39 psi?

Answer:

0.110 ft3/s

Loss of catalyst particles in stack gas.

(a)

Estimate the maximum diameter of microspherical catalyst particles that could be lost in

the stack gas of a fluid cracking unit under the following conditions:

Gas velocity at axis of stack

1.0 ft/s (vertically upward)

Gas viscosity

0.026 cp

Gas density

0.045 lb/ft3

Density of a catalyst particle

1.2 g/cm3

Express the result in microns (1 micron

10-~rn

lpm).

(b)

Is it permissible to use Stokes' law in (a)?

Answers:

(a) 110 pm; Re

0.93

Problems

2B.1

Different choice of coordinates for the falling film problem. Rederive the velocity profile

and the average velocity in s2.2, by replacing

by a coordinate

measured away from the

wall; that is,

is the wall surface, and

is the liquid-gas interface. Show that the ve-

locity distribution is then given by

and then use this to get the average velocity. Show how one can get Eq. 2B.1-1 from Eq. 2.2-18

by making a change of variable.

Alternate procedure for solving flow problems. In this chapter we have used the following

procedure:

(i)

derive an equation for the momentum flux, (ii) integrate this equation, (iii) insert

Newton's law to get a first-order differential equation for the velocity, (iv) integrate the latter

to get the velocity distribution. Another method is: (i) derive an equation for the momentum

flux, (ii) insert Newton's law to get a second-order differential equation for the velocity profile,

(iii) integrate the latter to get the velocity distribution. Apply this second method to the falling

film problem by substituting Eq.

2.2-14

into Eq. 2.2-10 and continuing as directed until the ve-

locity distribution has been obtained and the integration constants evaluated.

28.3

Laminar flow in

narrow slit (see Fig. 2B.3).

Fluid

Fig.

2B.3

Flow through a slit, with

(a)

Newtonian fluid is in laminar flow in a narrow slit formed by two parallel walls a dis-

tance

apart. It is understood that

W, so that "edge effects" are unimportant. Make a

differential momentum balance, and obtain the following expressions for the momentum-flux

and velocity distributions:

In these expressions

pgh

pgz.

(b)

What is the ratio of the average velocity to the maximum velocity for this flow?

(c)

Obtain the slit analog of the Hagen-Poiseuille equation.

(d)

Draw a meaningful sketch to show why the above analysis is inapplicable if

(e) How can the result in

(b)

be obtained from the results of

§2.5?

Chapter 2 Shell Momentum Balances and Velocity Distributions in Laminar Flow

2B.4

Laminar slit flow with

moving wall ("plane Couette flow").

Extend Problem 2B.3 by al-

lowing the wall at

to move in the positive

direction at a steady speed

v,.

Obtain

(a)

the

shear-stress distribution and

(b)

the velocity distribution. Draw carefully labeled sketches of

these functions.

2B.5

Interrelation of slit and annulus formulas.

When an annulus is very thin, it may, to a good

approximation, be considered as a thin slit. Then the results of Problem 2B.3 can be taken over

with suitable modifications. For example, the mass rate of flow in an annulus with outer wall

of radius

and inner wall of radius (1

s)R,

where

is small, may be obtained from Problem

2B.3 by replacing 2B by

EX,

and

by 2dl

;.SIR.

In this way we get for the mass rate of flow:

Show that this same result may be obtained from

Eq.

2.4-17 by setting

equal to 1

every-

where in the formula

and

then expanding the expression for

in powers of

This requires

using the Taylor series (see 5C.2)

and then performing a long division. The first term in the resulting series

will

be Eq. 2B.5-1.

Cau-

tion:

In the derivation it is necessary to use the first

four

terms of the Taylor series

Eq.

2B.5-2.

2B.6

Flow of a film on

the

outside of a circular tube

(see Fig. 2B.6). In a gas absorption experi-

ment

viscous fluid flows upward through a small circular tube and then downward in lami-

nar flow on the outside. Set up

momentum balance over a shell of thickness

in the film,

Velocity

distribution

outside

film

z-Momentum

out of shell

of thickness

Gravity force

acting on

the volume

2mArL

Fig.

2B.6

Velocity distribution and z-momentum

balance for the flow of a falling film on the outside

of a circular tube.

Problems

as shown in Fig. 2B.6. Note that the "momentum in" and "momentum out" arrows are al-

ways taken in the positive coordinate direction, even though in this problem the momentum

is flowing through the cylindrical surfaces in the negative

direction.

(a) Show that the velocity distribution in the falling film (neglecting end effects) is

(b)

Obtain an expression for the mass rate of flow in the film.

(c)

Show that the result in

(b)

simplifies to

Eq.

2.2-21 if the film thickness is very small.

2B.7

Annular flow with inner cylinder moving axially (see Fig. 2B.7).

cylindrical rod of radius

moves axially with velocity v,

vo along the axis of a cylindrical cavity of radius R as seen

in the figure. The pressure at both ends of the cavity is the same, so that the fluid moves

through the annular region solely because of the rod motion.

Rod of radius

KR-

moving with velocity

Cylinder of inside

Fig.

2B.7

Annular flow with the inner cylinder moving axially.

(a) Find the velocity distribution in the narrow annular region.

(b) Find the mass rate of flow through the annular region.

(c)

Obtain the viscous force acting on the rod over the length

(d) Show that the result in (c) can be written as a "plane slit" formula multiplied by a "curva-

ture correction." Problems of this kind arise in studying the performance of wire-coating dies.'

Fluid

modified

pressure

Fluid

modified

pressure

v, In (r/R)

Answers: (a)

vo In

radius

2dpv,

(d)

As2

where

(see Problem 2B.5)

2B.8

Analysis of a capillary flowmeter (see Fig.

2B.8).

Determine the rate of flow (in lb/hr)

through the capillary flow meter shown in the figure. The fluid flowing in the inclined tube is

Fig.

2B.8

capillary flow meter.

B. Paton,

Squires,

Darnell,

Cash, and

Carley,

Processing of Themoplastic

Materials,

Bernhardt (ed.), Reinhold, New York

(19591,

Chapter

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

water at 20"C, and the manometer fluid is carbon tetrachloride (CCl,) with density 1.594

g/cm3. The capillary diameter is 0.010 in. Note: Measurements of

and

are sufficient to cal-

culate the flow rate;

need not be measured. Why?

2B.9

Low-density phenomena in compressible tube

flodr3

(Fig. 2B.9). As the pressure is de-

creased in the system studied in Example 2.3-2, deviations from Eqs. 2.3-28 and 2.3-29 arise.

The gas behaves as if it slips at the tube wall. It is conventional2 to replace the customary "no-

slip" boundary condition that

0 at the tube wall by

in which

is the slip coefficient. Repeat the derivation in Example 2.3-2 using Eq. 2B.9-1 as the

boundary condition. Also make use of the experimental fact that the slip coefficient varies in-

versely with the pressure

(

Jo/p, in which

is a constant. Show that the mass rate of flow is

in which pa,,

$(po

p,).

When the pressure is decreased further, a flow regime is reached in which the mean free

path of the gas molecules is large with respect to the tube radius (Knudsen

flow).

In that

regime3

in which m is the molecular mass and

is the Boltzmann constant. In the derivation of this re-

sult it is assumed that all collisions of the molecules with the solid surfaces are diffuse and not

specular. The results in Eqs. 2.3-29,2B.9-2, and 2B.9-3 are summarized in Fig.

2B.9.

,Free molecule flow

or Knudsen flow

PO-

-1

Poiseuille flow

Fig.

28.9

A comparison of the flow regimes

Pavg

in gas flow through a tube.

2B.10

Incompressible flow

a slightly tapered tube.

An incompressible fluid flows through a tube

of circular cross section, for which the tube radius changes linearly from

at the tube en-

trance to a slightly smaller value

at the tube exit. Assume that the Hagen-Poiseuille equa-

tion is approximately valid over a differential length,

dz,

the

tube so that the mass flow rate is

This is a differential equation for

as a function of z, but, when the explicit expression for

X(z)

is inserted, it is not easily solved.

Kennard,

Kinetic Theory

Gases,

McGraw-Hill, New York (1938),

pp.

292-295,300-306.

Knudsen,

The Kinetic Theory of Gases,

Methuen, London, 3rd edition (1950). See also

Silbey

and

Alberty,

Physicnl Chemistry,

Wiley, New York, 3rd edition (2001), 517.6.