Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

g3.6

Use of the Equations of Change to Solve Flow Problems

In Chapter 1 we gave the components of the stress tensor in Cartesian coordinates,

and in this chapter we have derived the equations of continuity and motion in Cartesian

coordinates. In Tables

B.1,

and

we summarize these key equations in three

much-used coordinate systems: Cartesian

(x,

z),

cylindrical (r, 0,

z),

and spherical (r, 0,

4).

Beginning students should not concern themselves with the derivation of these equa-

tions, but they should be very familiar with the tables in Appendix

and be able to use

them for setting up fluid dynamics problems. Advanced students will want to go

through the details of Appendix A and learn how to develop the expressions for the var-

ious V-operations, as is done in 55A.6 and

A.7.

In this section we illustrate how to set up and solve some problems involving the

steady, isothermal, laminar flow of Newtonian fluids. The relatively simple analytical

solutions given here are not to be regarded as ends in themselves, but rather as a prepa-

ration for moving on to the analytical or numerical solution of more complex problems,

the use of various approximate methods, or the use of dimensional analysis.

The complete solution of viscous flow problems, including proofs of uniqueness and

criteria for stability, is a formidable task. Indeed, the attention of some of the world's best

applied mathematicians has been devoted to the challenge of solving the equations of con-

tinuity and motion. The beginner may well feel inadequate when faced with these equa-

tions for the first time. All we attempt to do in the illustrative examples in this section is to

solve a few problems for stable flows that are known to exist.

each case we begin by

making some

postulates

about the form for the pressure and velocity distributions: that is,

guess

how

and

should depend on position

the problem being studied. Then we

discard all the terms in the equations of continuity and motion that are unnecessary ac-

cording to the postulates made. For example, if one postulates that

is a function of

alone, terms like

dv,/dx

and

d2v,/dz2

can be discarded. When all the unnecessary terms

have been eliminated, one is frequently left with a small number of relatively simple equa-

tions; and if the problem is sufficiently simple, an analytical solution can be obtained.

It must be emphasized that in listing the postulates, one makes use of

intuition.

The

latter is based on our daily experience with flow phenomena. Our intuition often tells us

that a flow will be symmetrical about an axis, or that some component of the velocity is

zero. Having used our intuition to make such postulates, we must remember that the

final solution is correspondingly restricted. However, by starting with the equations of

change, when we have finished the "discarding process" we do at least have a complete

listing of all the assumptions used in the solution. In some instances it is possible to go

back and remove some of the assumptions and get a better solution.

In several examples to be discussed, we will find one solution to the fluid dynamical

equations. However, because the full equations are nonlinear, there may be other solutions

to the problem. Thus a complete solution to a fluid dynamics problem requires the specifi-

cation of the limits on the stable flow regimes as well as any ranges of unstable behavior.

That is, we have to develop a "map" showing the various flow regimes that are possible.

Usually analytical solutions can be obtained for only the simplest flow regimes; the re-

mainder of the information is generally obtained by experiment or by very detailed nu-

merical solutions. In other words, although we know the differential equations that govern

the fluid motion, much is yet unknown about how to solve them. This is a challenging area

of applied mathematics, well above the level of an introductory textbook.

When difficult problems are encountered, a search should be made through some of

the advanced treatises on fluid dynamics.'

Berker,

Handbuch der Physik,

Volume

VIII-2,

Springer, Berlin (1963),

pp.

1-384;

Batchelor,

An Infroduction to Fluid Mechanics,

Cambridge University Press (1967); L. Landau and

Lifshitz,

Fluid

Mechanics,

Pergamon Press, Oxford, 2nd edition (1987);

Schetz and

Fuhs (eds.),

Handbook

Fluid

Dynamics and Fluid Machinery,

Wiley-Interscience, New York (1996);

W. Johnson (ed.),

The Handbook

Fluid Dynamics,

CRC Press, Boca Raton, Fla. (1998); C. Y. Wang,

Ann. Revs. Fluid Mech.,

23,159-177 (1991).

Chapter 3 The Equations of Change for Isothermal Systems

We now turn to the illustrative examples. The first two are problems that were dis-

cussed in the preceding chapter; we rework these just to illustrate the use of the equa-

tions of change. Then we consider some other problems that would be difficult to set up

by the shell balance method of Chapter

Rework the tube-flow problem of Example 2.3-1 using the equations of continuity and mo-

tion. This illustrates the use of the tabulated equations for constant viscosity and density in

Long

cylindrical coordinates, given in Appendix B.

Circular Tube

SOLUTION

We postulate that

6,v,(r, z). This postulate implies that there is no radial flow (v,

0) and

no tangential flow (v,

O),

and that v, does not depend on 8. Consequently, we can discard

many terms from the tabulated equations of change, leaving

equation of continuity

dv,

(3.6-1)

r-equation of motion

o=--

(3.6-2)

&equation of motion

o=--

(3.6-3)

z-equation of motion

The first equation indicates that v, depends only on r; hence the partial derivatives in the sec-

ond term on the right side of Eq. 3.6-4 can be replaced by ordinary derivatives. By using the

modified pressure

pgh

(where

is the height above some arbitrary datum plane), we

avoid the necessity of calculating the components of

in cylindrical coordinates, and we ob-

tain a solution valid for any orientation of the axis of the tube.

Equations 3.6-2 and 3.6-3 show that

is a function of z alone, and the partial derivative

in the first term of Eq. 3.6-4 may be replaced by an ordinary derivative. The only way that we

can have a function of r plus a function of z equal to zero is for each term individually to be a

constant-say, Co-so that Eq. 3.6-4 reduces to

The

equation can be integrated at once. The v,-equation can be integrated by merely "peel-

ing off" one operation after another on the left side (do not "work out" the compound deriva-

tive there). This gives

C+

(3.6-6)

The four constants of integration can be found from the boundary conditions:

B.C.

B.C. 3

B.C.

atz=O, 9=Y0

at z

9[,

at r

finite

The resulting solutions are:

(yo

gL)(2/L)

53.6

Use of the Equations of Change to Solve Flow Problems

Equation 3.6-13 is the same as Eq. 2.3-18. The pressure profile in Eq. 3.6-12 was not obtained

in Example 2.3-1, but was tacitly postulated; we could have done that here, too, but we chose

to work with a minimal number of postulates.

As pointed out in Example 2.3-1, Eq. 3.6-13 is valid only in the laminar-flow regime, and

at locations not too near the tube entrance and exit. For Reynolds numbers above about 2100,

a turbulent-flow regime exists downstream of the entrance region, and Eq. 3.6-13 is no longer

valid.

Set up the problem in Example 2.2-2 by using the equations of Appendix

This illustrates

the use of the equation of motion in terms of

Falling Film with

Variable Viscosity

SOLUTION

As in Example 2.2-2 we postulate a steady-state flow with constant density, but with viscosity

depending on x. We postulate, as before, that the x- and y-components of the velocity are zero

and that

v,(x).

With these postulates, the equation of continuity is identically satisfied.

According to Table

B.l,

the only nonzero components of

are

T,,

r,,

-,u(dv,/dx).

The

components of the equation of motion in terms of

are, from Table B.5,

where

is the angle shown in Fig. 2.2-2.

Integration of Eq. 3.6-14 gives

pgx sin

(

(3.6-1

in which

f(y,

is an arbitrary function. Equation 3.6-15 shows that

cannot be

function of

We next recognize that the pressure in the gas phase is very nearly constant at the prevailing

atmospheric pressure

pa,,.

Therefore, at the gas-liquid interface x

0, the pressure is also

constant at the value

pa,,.

Consequently,

can be set equal to

pa,

and we obtain finally

Equation 3.5-16 then becomes

T,,

pg cos

which is the same as Eq. 2.2-10. The remainder of the solution is the same as in 52.2.

We mentioned earlier that the measurement of pressure difference vs. mass flow rate through

a cylindrical tube is the basis for the determination of viscosity in commercial capillary vis-

Operation

a Couette

cometers. The viscosity may also be determined by measuring the torque required to turn a

Viscometer

solid object in contact with a fluid. The forerunner of all rotational viscometers is the Couette

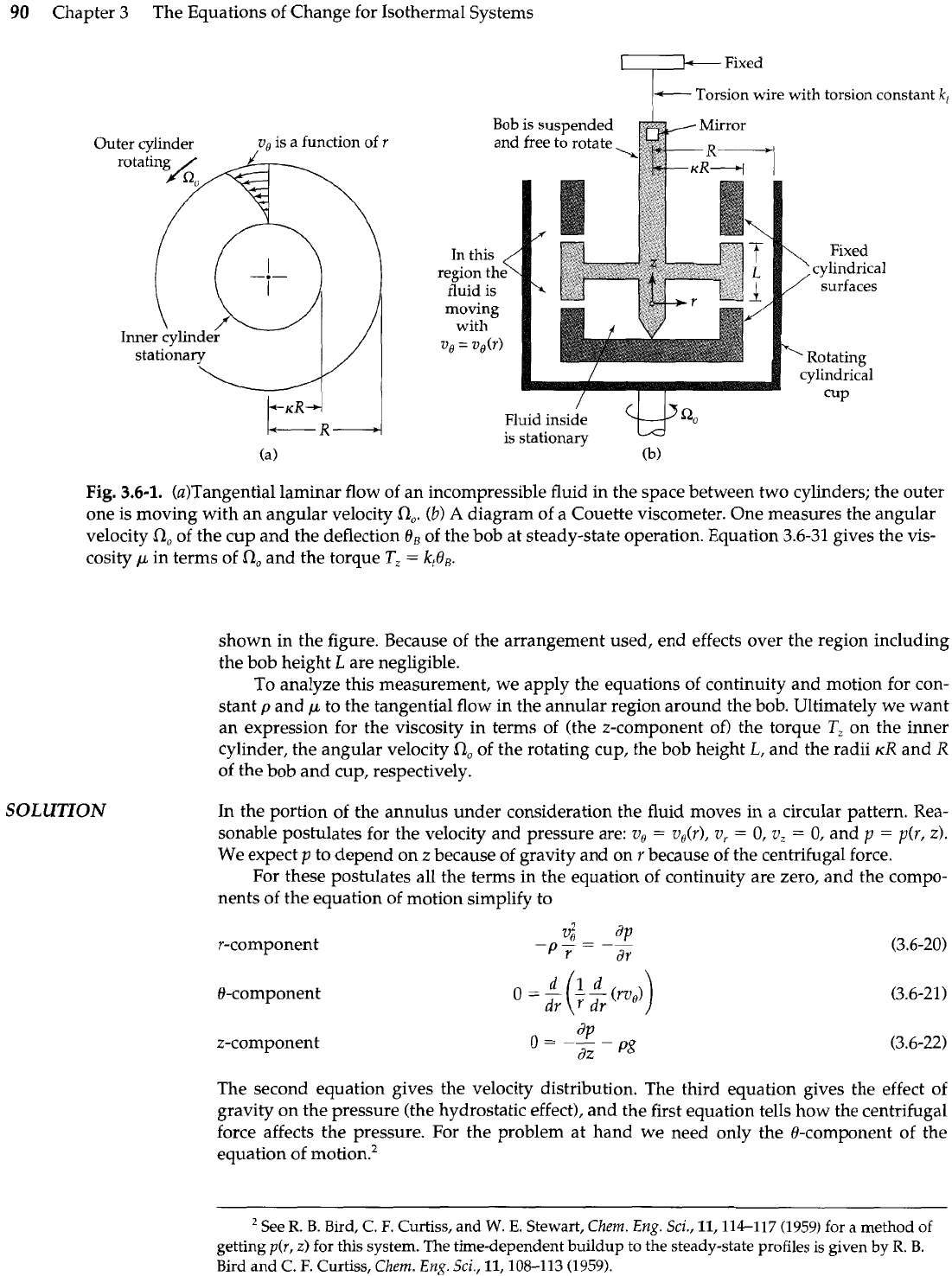
instrument, which is sketched in Fig. 3.6-1.

The fluid is placed in the cup, and the cup is then made to rotate with a constant angular

velocity

Ln,

(the subscript

"0"

stands for outer). The rotating viscous liquid causes the sus-

pended bob to turn until the torque produced by the momentum transfer in the fluid equals

the product of the torsion constant

and the angular displacement

of the bob. The angular

displacement can be measured by observing the deflection of a light beam reflected from a

mirror mounted on the bob. The conditions of measurement are controlled so that there is a

steady, tangential, laminar flow in the annular region between the two coaxial cylinders

Chapter

The Equations of Change for Isothermal Systems

Torsion wire with torsion constant

Fig.

3.6-1.

(a)Tangential laminar flow of an incompressible fluid in the space between two cylinders; the outer

one is moving with an angular velocity

In,.

(b)

diagram of a Couette viscometer. One measures the angular

velocity

Ino

of the cup and the deflection

of the bob at steady-state operation. Equation 3.6-31 gives the vis-

cosity

in terms of

and the torque

kt&.

is a function of

shown in the figure. Because of the arrangement used, end effects over the region including

the bob height

are negligible.

To analyze this measurement, we apply the equations of continuity and motion for con-

stant

and

to the tangential flow in the annular region around the bob. Ultimately we want

an expression for the viscosity in terms of (the z-component of) the torque

on the inner

cylinder, the angular velocity

of the rotating cup, the bob height

and the radii

and

of the bob and cup, respectively.

Ir.">-

SOLUTION

Fluid inside

In the portion of the annulus under consideration the fluid moves in

circular pattern. Rea-

sonable postulates for the velocity and pressure are: v,

v,(r),

and

p(r,

2).

We expect p to depend on z because of gravity and on r because of the centrifugal force.

For these postulates all the terms in the equation of continuity are zero, and the compo-

nents of the equation of motion simplify to

(a)

r-component

z-component

The second equation gives the velocity distribution. The third equation gives the effect of

gravity on the pressure (the hydrostatic effect), and the first equation tells how the centrifugal

force affects the pressure. For the problem at hand we need only the 13-component of the

equation of m~tion.~

See

Bird,

Curtiss, and

Stewart,

Chem.

Eng.

Sci.,

11,114-117 (1959) for a method of

getting

p(r,

for this system. The time-dependent buildup to the steady-state profiles is given by

Bird and

Curtiss,

Chem.

Eng.

Sci.,

11,108-113 (1959).

53.6

Use of the Equations of Change to Solve Flow Problems

novice might have a compelling urge to perform the differentiations in

Eq.

3.6-21 be-

fore solving the differential equation, but this should not be done. All one has to do is "peel

off" one operation at a time-just the way you undress-as follows:

rv,

C,?

(3.6-25)

The boundary conditions are that the fluid does not slip at the two cylindrical surfaces:

B.C.

These boundary conditions can be used to get the constants of integration, which are then in-

serted in

Eq.

3.6-26. This gives

By writing the result

this form,

with

similar terms

the numerator and denominator, it is clear

that both boundary conditions are satisfied and that the equation is dimensionally consistent.

From the velocity distribution we can find the momentum flux by using Table

B.2:

The torque acting on the inner cylinder is then given by the product of the inward momen-

tum flux

(-T,,),

the surface of the cylinder, and the lever arm, as follows:

The torque is also given by

kt&,.

Therefore, measurement of the angular velocity of the

cup and the angular deflection of the bob makes it possible to determine the viscosity. The

same kind of analysis is available for other rotational viscometers."

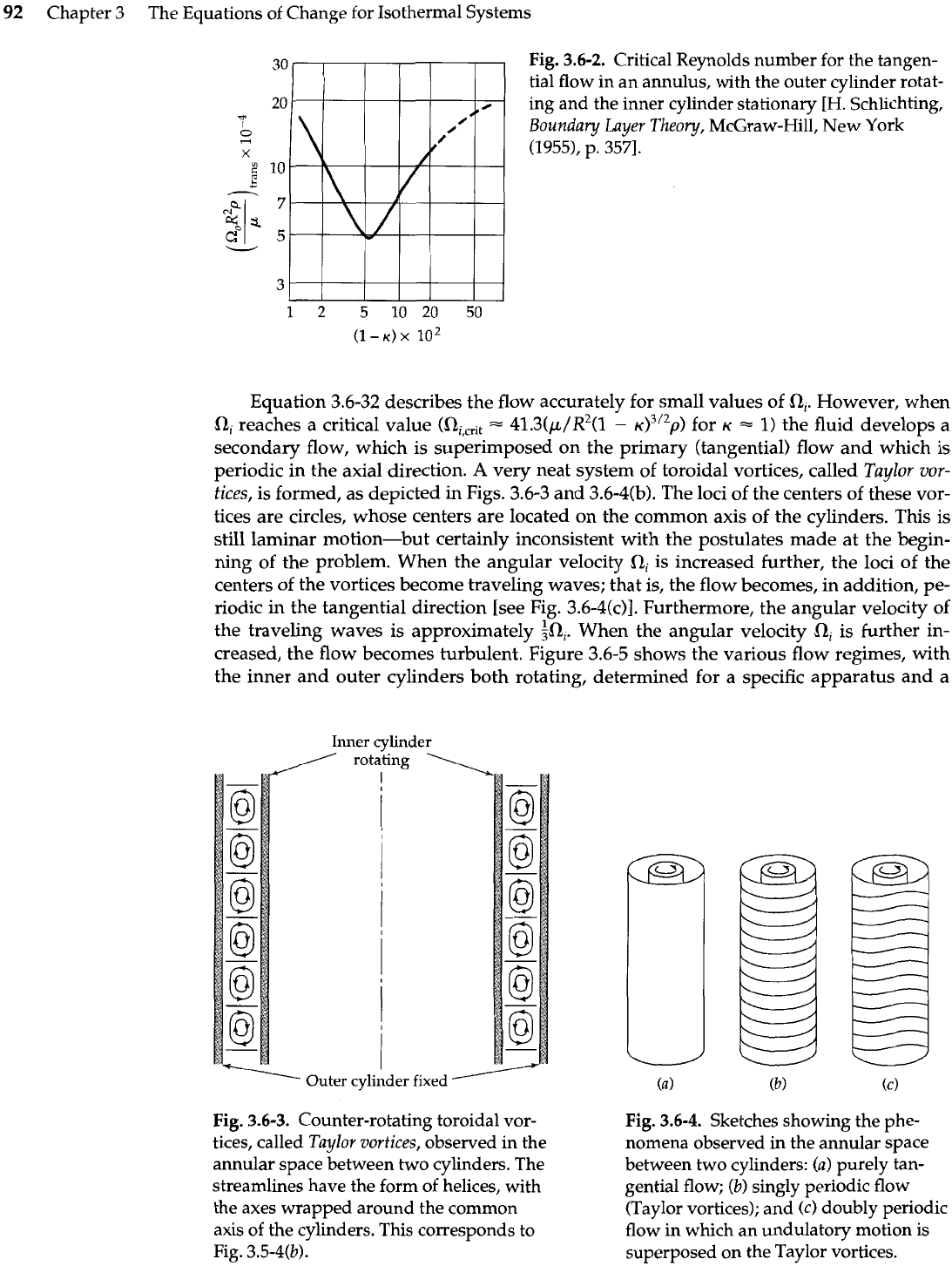
For any viscometer it is essential to know when turbulence will occur. The critical

Reynolds number

(LR$2p/p),,,

above which the system becomes turbulent, is shown in

Fig.

3.6-2 as a function of the radius ratio

One might ask what happens if we hold the outer cylinder fixed and cause the inner

cylinder to rotate with an angular velocity

ili

(the subscript

"i"

stands for inner). Then

the velocity distribution is

This is obtained by making the same postulates (see before

Eq.

3.6-20) and solving the

same differential equation

(Eq.

3.6-21), but with a different set of boundary conditions.

VanWazer,

W. Lyons,

Kim,

and

Colwell,

Viscosity and Flow Measurement,

Wiley,

New York (1963);

Walters,

Rheomety,

Chapman and Hall, London (1975).

92 Chapter

The Equations of Change for Isothermal Systems

Fig.

3.6-2.

Critical Reynolds number for the tangen-

tial flow in an annulus, with the outer cylinder rotat-

ing and the inner cylinder stationary

[H.

Schlichting,

Bounds

Layer Theo

McGraw-Hill, New York

(1955), p. 3571.

2Qlx

I I

20 50

lo2

Equation 3.6-32 describes the flow accurately for small values of

Ri.

However, when

reaches a critical value

(C&,

41.3(~/~'(1

K)~"~)

for

the fluid develops a

secondary flow, which is superimposed on the primary (tangential) flow and which is

periodic in the axial direction.

very neat system of toroidal vortices, called Taylor

vor-

tices,

is formed, as depicted in Figs. 3.6-3 and 3.6-4(b). The loci of the centers of these vor-

tices are circles, whose centers are located on the common axis of the cylinders. This is

still laminar motion-but certainly inconsistent with the postulates made at the begin-

ning of the problem. When the angular velocity

is increased further, the loci of the

centers of the vortices become traveling waves; that is, the flow becomes, in addition, pe-

riodic in the tangential direction [see Fig. 3.6-4(c)I. Furthermore, the angular velocity of

the traveling waves is approximately

;ai.

When the angular velocity

is further in-

creased, the flow becomes turbulent. Figure 3.6-5 shows the various flow regimes, with

the inner and outer cylinders both rotating, determined for a specific apparatus and a

Inner cylinder

rotating

Outer

cylinder

fixed

Fig.

3.6-3.

Counter-rotating toroidal vor-

Fig. 3.6-4.

Sketches showing the phe-

tices, called

Taylor

vortices, observed in the

nomena observed in the annular space

annular space between two cylinders. The

between two cylinders:

(a)

purely tan-

streamlines have the form of helices, with

gential flow;

(b)

singly periodic flow

the axes wrapped around the common

(Taylor vortices); and

(c)

doubly periodic

axis of the cylinders. This corresponds to

flow in which an undulatory motion is

Fig. 3.5-4(b).

superposed on the Taylor vortices.

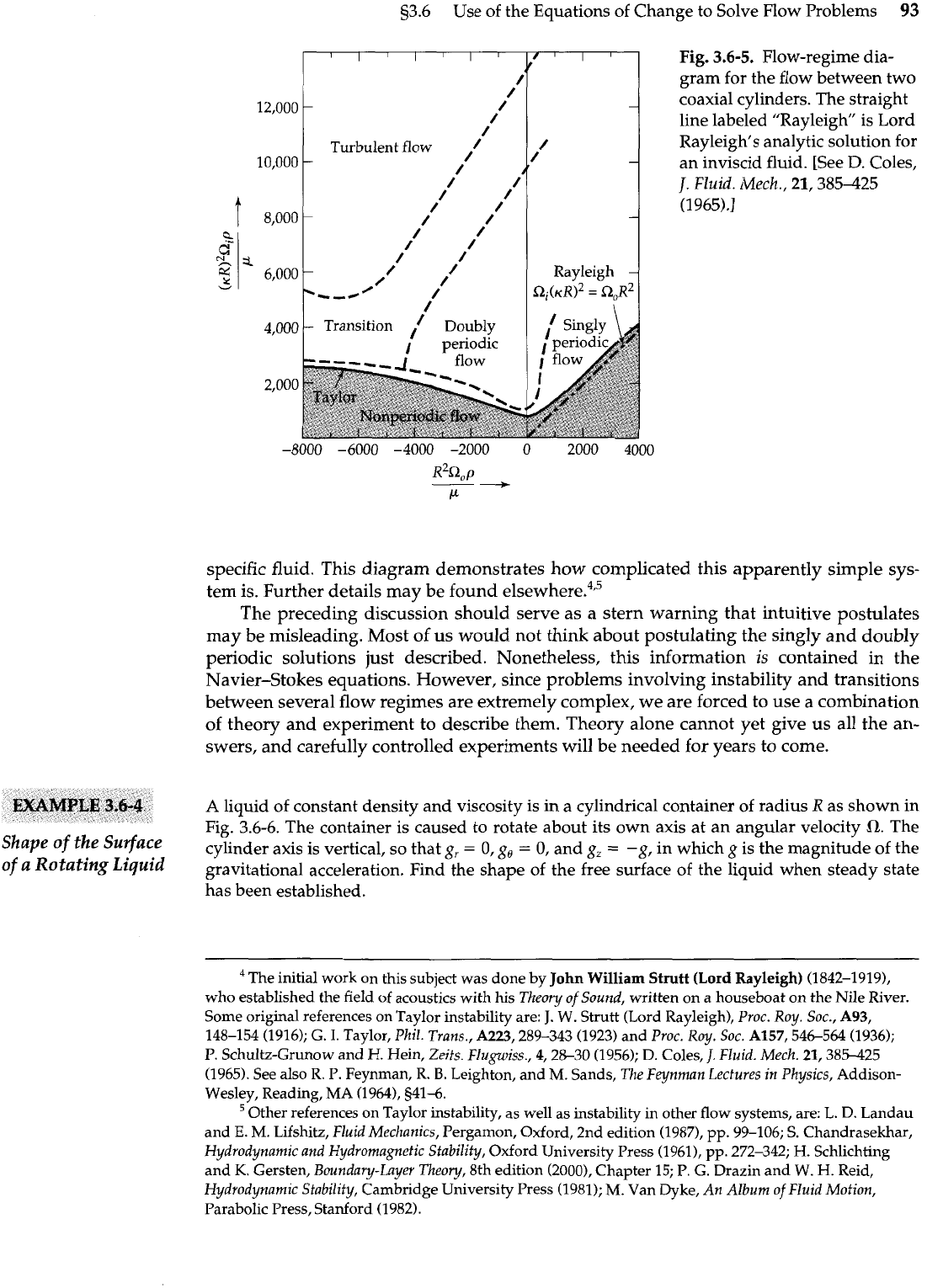
53.6 Use of the Equations of Change to Solve Flow Problems

Turbulent flow

10,000

8,000

Fig.

3.6-5.

Flow-regime dia-

gram for the flow between two

coaxial cylinders. The straight

line labeled "Rayleigh" is Lord

Rayleigh's analytic solution for

an inviscid fluid. [See

Coles,

Fluid.

Mech.,

21,385425

(1965).1

specific fluid. This diagram demonstrates how complicated this apparently simple sys-

tem is. Further details may be found el~ewhere.~~~

The preceding discussion should serve as a stern warning that intuitive postulates

may be misleading. Most of us would not think about postulating the singly and doubly

periodic solutions just described. Nonetheless, this information

contained in the

Navier-Stokes equations. However, since problems involving instability and transitions

between several flow regimes are extremely complex, we are forced to use a combination

of theory and experiment to describe them. Theory alone cannot yet give us all the an-

swers, and carefully controlled experiments will be needed for years to come.

liquid of constant density and viscosity is in a cylindrical container of radius

as shown in

Fig. 3.6-6. The container is caused to rotate about its own axis at an angular velocity

The

the

Su*face

cylinder axis is vertical, so that

and

-g,

in which

is the magnitude

the

a Rotating Liquid

gravitational acceleration. Find the shape of the free surface of the liquid when steady state

has been established.

The initial work on this subject was done by

John

William

Strutt

(Lord

Rayleigh)

(1842-1919),

who established the field of acoustics with his

Theory of Sound,

written on a houseboat on the Nile River.

Some original references on Taylor instability are:

Strutt (Lord Rayleigh),

Proc. Roy. Soc.,

A93,

148-154 (1916);

Taylor,

Phil. Trans.,

A223,289-343 (1923) and

Proc. Roy. Soc.

A157,546-564 (1936);

Schultz-Grunow and

Hein,

Zeits. Flugwiss.,

4,28-30 (1956); D. Coles,

Fluid. Mech.

21,385-425

(1965). See also

P. Feynman, R.

Leighton, and

Sands,

The

Feynman Lectures in Physics,

Addison-

Wesley, Reading,

(1964),§41-6.

Other references on Taylor instability, as well as instability in other flow systems, are:

Landau

and

Lifshitz,

Fluid Mechanics,

Pergamon, Oxford, 2nd edition (1987), pp. 99-106;

Chandrasekhar,

Hydrodynamic and Hydromagnetic Stability,

Oxford University Press (1961), pp. 272-342;

Schlichting

and

Gersten,

Boundary-Layer Theory,

8th edition (2000), Chapter 15;

G. Drazin and

Reid,

Hydrodynamic Stability,

Cambridge University Press (1981);

Van Dyke,

An Album of Fluid Motion,

Parabolic Press, Stanford (1982).

Chapter

The Equations of Change for Isothermal Systems

SOLUTION

Fig.

3.6-6.

Rotating liquid with a free surface, the

shape of which is a paraboloid of revolution.

for this problem, and the equations of change are

given in Tables

B.2

and B.6. At steady state we postulate that

and viare both zero and that

depends only on r. We also postulate that p depends

because of the gravitational force

and on r because of the centrifugal force but not on 6.

These postulates give 0

for the equation of continuity, and the equation of motion gives:

R-I

Cylindrical coordinates are appropriate

Patm

surface

r-component

z-component

p(r,

within fluid

The 6-component of the equation of motion can be integrated to give

in which

and

are constants of integration. Because

cannot be infinite at r

0, the con-

stant

must be zero. At r

the velocity v, is

Rfl.

Hence

2i2 and

This states that each element of the rotating liquid moves as an element of a rigid body (we

could have actually postulated that the liquid would rotate as a rigid body and written down

Eq. 3.6-37 directly). When the result in

Eq.

3.6-37 is substituted into Eq. 3.6-33, we then have

these two equations for the pressure gradients:

pf12r and

-pg

Each of these equations can be integrated, as follows:

;pi2'r2

f,@, z)

and

-pgz

f2(r, 6)

(3.6-40,41)

where

and

are arbitrary functions of integration. Since we have postulated that p does not

depend on

we can choose

-pgz

and

$a2$

where

is a constant, and sat-

isfy Eqs. 3.6-38 and 39. Thus the solution to those equations has the form

The constant

may be determined by requiring that

pa,, at r

and z

z,,

the latter

being the elevation of the liquid surface at r

When

is obtained in this way, we get

s3.6

Use of the Equations of Change to Solve Flow Problems

This equation gives the pressure at all points within the liquid. Right at the liquid-air inter-

face, p

p,,,,

and with this substitution Eq. 3.6-43 gives the shape of the liquid-air interface:

This is the equation for a parabola. The reader can verify that the free surface of a liquid in

rotating annular container obeys

similar relation.

solid sphere of radius

is rotating slowly at a constant angular velocity

in a large body

of quiescent fluid (see Fig. 3.6-7). Develop expressions for the pressure and velocity distribu-

near

Slowly

tions in the fluid and for the torque

required to maintain the motion. It is assumed that the

Rotating Sphere

sphere rotates sufficiently slowly that it is appropriate to use the creeping

flow

version of the

equation of motion in Eq. 3.5-8. This problem illustrates setting up and solving a problem in

spherical coordinates.

SOLUTION

The equations of continuity and motion in spherical coordinates are given in Tables B.4 and

B.6, respectively. We postulate that, for steady creeping flow, the velocity distribution will

have the general form

6,v,(r, O), and that the modified pressure will be of the form

(r, 8). Since the solution is expected to be symmetric about the z-axis, there is no depen-

dence on the angle

With these postulates, the equation of continuity is exactly satisfied, and the components

of the creeping flow equation of motion become

r-component

(3.6-45)

The boundary conditions may be summarized as

B.C. 1:

B.C. 2:

B.C. 3:

at r

0, v,

Rfl

sin

asr+m, vr+O,v,+O,vd+O

asr+m, 9+p0

where

pgz,

and

is the fluid pressure far from the sphere at

Equation 3.6-47 is a partial differential equation for v,(r, 0). To solve this, we try a solu-

tion of the form v,

(r)

sin 0. This is just

guess, but it is consistent with the boundary con-

dition in Eq. 3.6-48. When this trial form for the velocity distribution is inserted into Eq. 3.6-47

we get the following ordinary differential equation for

(r):

Torque

required

to make the sphere

rotate

Fig.

3.6-7.

slowly rotating sphere in an infinite expanse

of fluid. The primary flow is

OR(R/U)~ sin 8.

Chapter 3 The Equations of Change for Isothermal Systems

This is an "equidimensional equation," which may be solved by assuming a trial solution

(see Eq. C.l-14). Substitution of this trial solution into Eq. 3.6-51 gives

-2.

The so-

lution of Eq. 3.6-51 is then

so that

Application of the boundary conditions shows that

and

aR3.

Therefore the final

expression for the velocity distribution is

sin

(R)'

Next we evaluate the torque needed to maintain the rotation of the sphere. This will be the in-

tegral, over the sphere surface, of the tangential force

(T,&=,)R~

sin

0dBd4

exerted on the fluid

by a solid surface element, multiplied by the lever arm

sin

for that element:

J:'

(3161 sin

B)(R

sin

B)R2

sin

BdBd4

In going from the first to the second line, we have used Table B.l, and in going from the sec-

ond to the third line we have done the integration over the range of the

variable. The inte-

gral in the third line is

As the angular velocity increases, deviations from the "primary flow" of Eq. 3.6-54 occur.

Because of the centrifugal force effects, the fluid is pulled in toward the poles of the sphere

and shoved outward from the equator as shown in Fig. 3.6-8. To describe this "secondary

flow," one has to include the

Vvl

term in the equation of motion. This can be done by the

use of a stream-function meth~d.~

Fig.

3.6-8.

Rough sketch showing the secondary flow

IIIIIIII

which appears around a rotating sphere as the Reynolds

Side view

number is increased.

See, for example, the development by

Hassager in

B. Bird,

Armstrong, and

Hassager,

Dynamics of Polymeric Liquids,

Vol. I., Wiley-Interscience, New York, 2nd edition (1987),

pp.

31-33.

See

also

L. Landau and

Lifshitz,

Fluid Mechanics,

Pergamon, Oxford, 2nd edition

(1987),

65;

and L.

Leal,

Laminar Flow and Convective Transport Processes,

Butterworth-Heinemann, Boston (1992), pp. 180-181.