Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

848 Electrical Circuit Theory and Technology

Problem 7. Two coils are connected in series and their effective

inductance is found to be 15 mH. When the connection to one coil

is reversed, the effective inductance is found to be 10 mH. If the

coefﬁcient of coupling is 0.7, determine (a) the self inductance of

each coil, and (b) the mutual inductance.

(a) From equation (43.13), total inductance, L D L

C L

š 2M

and from equation (43.9), M D k

L



hence L D L

C L

š 2k

L



Since in equation (43.11),

D 15 mH, 15 D L

C L

C 2k

L

43.15

and since in equation (43.12),

D 10 mH, 10 D L

C L

 2k

L

43.16

Equation 43.15 C equation (43.16) gives:

25 D 2L

C 2L

and 12.5 D L

C L

43.17

From equation (43.17), L

D 12.5  L

Substituting in equation (43.15), gives:

15 D L

C 12.5 L

 C 20.7

12.5  L

]

i.e., 15 D 12.5 C 1.4



12.5L

 L



15  12.5

1.4



12.5L

 L



and



15  12.5

1.4



D 12.5L

 L

i.e., 3.189 D 12.5L

 L

from which, L

 12.5L

C 3.189 D 0

Using the quadratic formula:

12.5 š



[12.5

 413.189]

21

i.e., L

12.5 š 11.98

D 12.24 mH or 0.26 H

From equation (43.17):

D 12.5  L

D 12.5  12.24 D 0.26 mH

or 12.5  0.26 D 12.24 mH

Magnetically coupled circuits 849

(b) From equation (43.14),

mutual inductance, M D

 L

15  10

D 1.25 mH

Further problems on coils in series may be found in Section 43.8, problems

7 to 11, page 865.

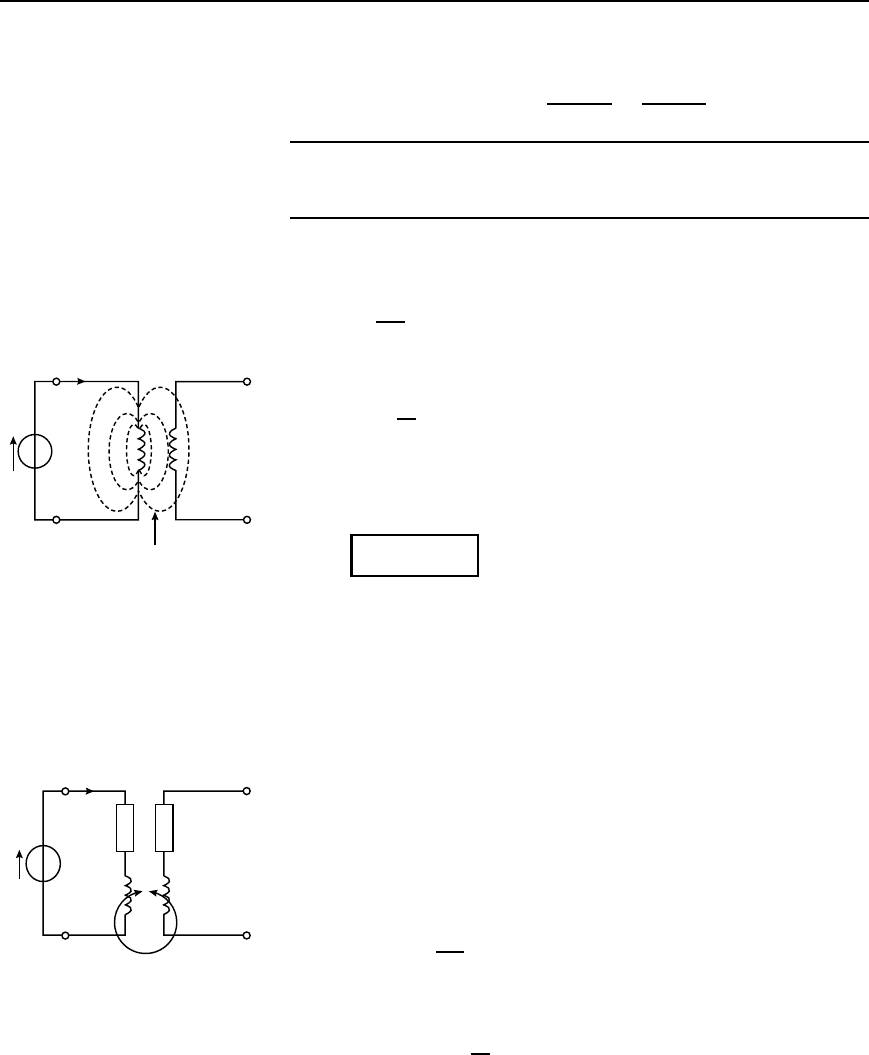
43.6 Coupled circuits

The magnitude of the secondary e.m.f. E

in Figure 43.5 is given by:

D M

, from equation (43.1)

If the current I

is sinusoidal, i.e., I

D I

sinωt

then E

D M

I

sinωt D MωI

cosωt

Since cos ωt D sinωt C 90

 then cosωt D j sinωt in complex form.

Hence E

D MωI

j sin ωt D jωMI

sinωt

i.e.,

= j!MI

43.18

Magnetic flux

Figure 43.5

If L

is the self inductance of the primary winding in Figure 43.5, there

will be an e.m.f. generated equal to jωL

induced into the primary

winding since the ﬂux set up by the primary current also links with the

primary winding.

(a) Secondary open-circuited

Figure 43.6 shows two coils, having self inductances of L

and L

which

are inductively coupled together by a mutual inductance M. The primary

winding has a voltage generator of e.m.f. E

connected across its termi-

nals. The internal resistance of the source added to the primary resistance

is shown as R

and the secondary winding which is open-circuited has a

resistance of R

Applying Kirchhoff’s voltage law to the primary circuit gives:

D I

C L

43.19

Figure 43.6

If E

and I

are both sinusoidal then equation (43.19) becomes:

D I

C L

I

sinωt

D I

C L

ωI

cosωt

D I

C L

ωjI

sinωt

850 Electrical Circuit Theory and Technology

i.e., E

D I

C jωI

D I

R

C jωL



i.e., I

C jωL

43.20

From equation (43.18), E

D jωMI

from which, I

jωM

43.21

Equating equations (43.20) and (43.21) gives:

j!M

C j!L

and

j!ME

Y j!L

43.22

Problem 8. For the circuit shown in Figure 43.7, determine the

p.d. E

which appears across the open-circuited secondary winding,

given that E

D 8sin2500t volts.

Impedance of primary, Z

D R

C jωL

D 15 Cj25005 ð 10

3



D 15 C j12.5 or 19.53

39.81



Primary current I

19.53

39.81

15 Ω 15 Ω

5 mH 5 mH

M = 0.1 mH

Figure 43.7

From equation (43.18),

D jωMI

jωME

R

C jωL



j25000.1 ð 10

3

8



19.53

39.81

19.53

39.81

D 0.102

50.19

Problem 9. Two coils x and y, with negligible resistance, have self

inductances of 20 mH and 80 mH respectively, and the coefﬁcient

of coupling between them is 0.75. If a sinusoidal alternating p.d.

of 5 V is applied to x, determine the magnitude of the open circuit

e.m.f. induced in y.

From equation (43.9), mutual inductance,

M D k



L

 D 0.75



[20 ð 10

3

80 ð 10

3

] D 0.03 H

Magnetically coupled circuits 851

From equation (43.22), the magnitude of the open circuit e.m.f. induced

in coil y,

jωME

C jωL

When R

D 0, jE

jωME

jωL

0.035

20 ð 10

3

D 7.5V

(b) Secondary terminals having load impedance

In the circuit shown in Figure 43.8 a load resistor R

is connected across

the secondary terminals. Let R

C R

D R

When an e.m.f. is induced into the secondary winding a current I

ﬂows and this will induce an e.m.f. into the primary winding.

Applying Kirchhoff’s voltage law to the primary winding gives:

D I

R

C jωL

 š jωMI

43.23

′

Figure 43.8

Applying Kirchhoff’s voltage law to the secondary winding gives:

0 D I

R

C jωL

 š jωMI

43.24

From equation (43.24), I

ÝjωI

R

C jωL



Substituting this in equation (43.23) gives:

D I

R

C jωL

 š jωM



ÝjωMI

R

C jωL





i.e., E

D I



R

C jωL

 C

R

C jωL





since j

D1

D I



R

C jωL

 C

R

 jωL



C ω



D I



C jωL

C ω



jω

C ω



The effective primary impedance Z

1eff

of the circuit is given by:

1.eff/

= R

Y !

Y j



−

Y !



43.25

In equation (43.25), the primary impedance is R

C jωL

. The

remainder,

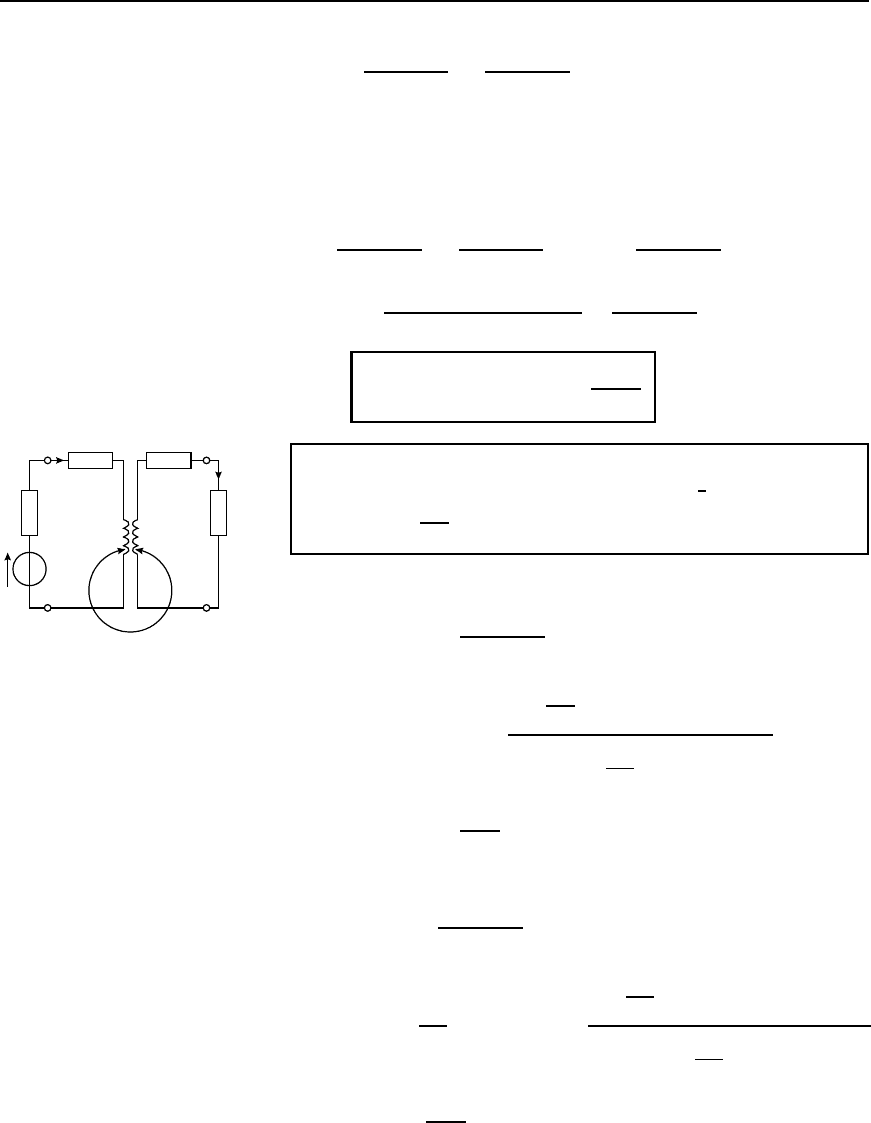
852 Electrical Circuit Theory and Technology

i.e.,



C ω

 j

C ω



is known as the reﬂected impedance since it represents the impedance

reﬂected back into the primary side by the presence of the secondary

current.

Hence reﬂected impedance

C ω

 j

C ω

D ω



 jωL

C ω



D ω

R

 jωL



R

C jωL

R

 jωL



C jωL

i.e.,

reﬂected impedance, Z

43.26

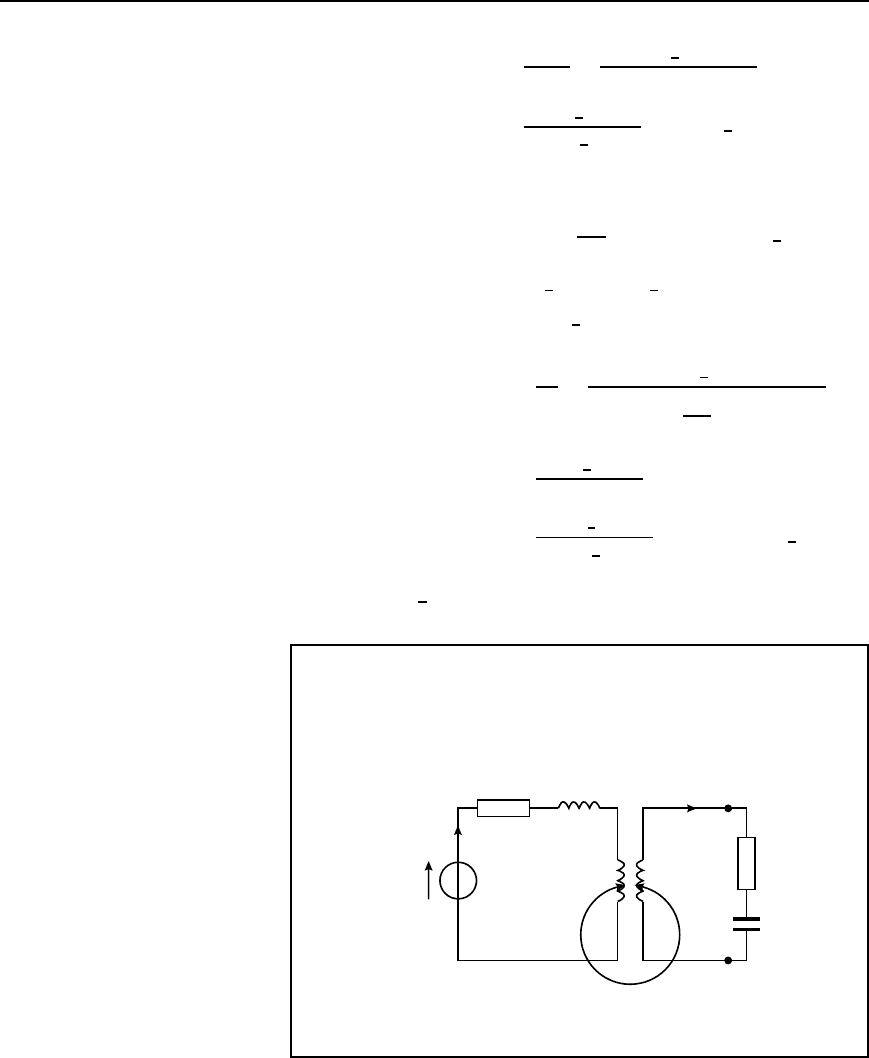
Problem 10. For the circuit shown in Figure 43.9, determine the

value of the secondary current I

if E

D 2

volts and the

frequency is



Hz.

16 Ω 16 Ω

50 Ω

4 Ω

10 mH 10 mH

M = 2 mH

Figure 43.9

From equation (43.25), R

1eff

is the real part of Z

1eff

i.e., R

1eff

D R

C ω

D 4 C 16 C



2





2 ð 10

3



16 C 50



2





10 ð 10

3



D 20 C

1056

4756

D 20.222 

and X

1eff

is the imaginary part of Z

1eff

, i.e.,

1eff

D ωL



C ω



2





10 ð 10

3

 



2





2 ð 10

3



10 ð 10

3





2





10 ð 10

3



D 20 

320

4756

D 19.933 

Magnetically coupled circuits 853

Hence primary current, I

1eff

20.222 C j19.933

28.395

44.59

D 0.0704

44.59

From equation (43.18), E

D jωMI

D j



2





2 ð 10

3

0.0704

44.59



D 4

0.0704

44.59



D 0.282

45.41

Hence secondary current I

0.282

45.41

66 C j



2





10 ð 10

3



0.282

45.41

66 C j20

0.282

45.41

68.964

16.86

D 4.089 ð 10

3

28.55

i.e., I

= 4.09

28.55

Problem 11. For the coupled circuit shown in Figure 43.10,

calculate (a) the self impedance of the primary circuit, (b) the self

impedance of the secondary circuit, (c) the impedance reﬂected into

the primary circuit, (d) the effective primary impedance, (e) the

primary current, and (f) the secondary current.

300 Ω

0.2 H

50∠0° V

w = 500 rad/s

0.5 H 0.3 H

500 Ω

5 µF

M = 0.2 H

Figure 43.10

(a) Self impedance of primary circuit, Z

D 300 C j5000.2 C 0.5

i.e., Z

= .300 Y j350/Z

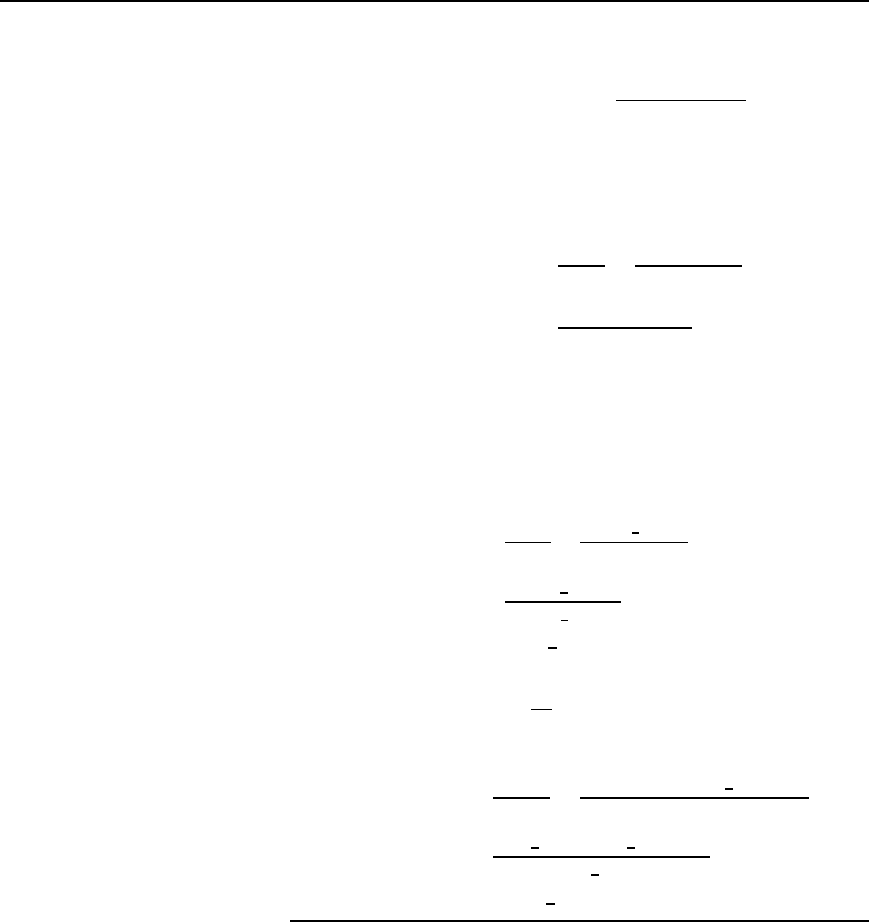
854 Electrical Circuit Theory and Technology

(b) Self impedance of secondary circuit,

D 500 C j



5000.3 

5005 ð 10

6



D 500 C j150  400

i.e., Z

= .500 − j250/Z

reﬂected impedance, Z

500

0.2

500  j250

500 C j250

500

C 250

D .16 Y j8/Z

(d) Effective primary impedance,

1eff

D Z

C Z

(note this is equivalent to equation 43.25)

D 300 C j350 C 16 Cj8

i.e., Z

1.eff/

= .316 Y j358/Z

(e) Primary current I

1eff

316 C j358

477.51

48.57

D 0.105

−48.57

(f) Secondary current, I

, where

D jωMI

from equation (43.18)

Hence I

jωMI

j5000.20.105

48.57



500  j250

100

0.105

48.57



559.02

26.57

D 0.0188

Tuning capacitors may be added to the primary and/or secondary circuits

to cause it to resonate at particular frequencies. These may be connected

either in series or in parallel with the windings. Figure 43.11 shows each

winding tuned by series-connected capacitors C

and C

. The expres-

sion for the effective primary impedance Z

1eff

, i.e., equation (43.25)

applies except that ωL

becomes ωL

 1/ωC

 and ωL

becomes

ωL

 1/ωC



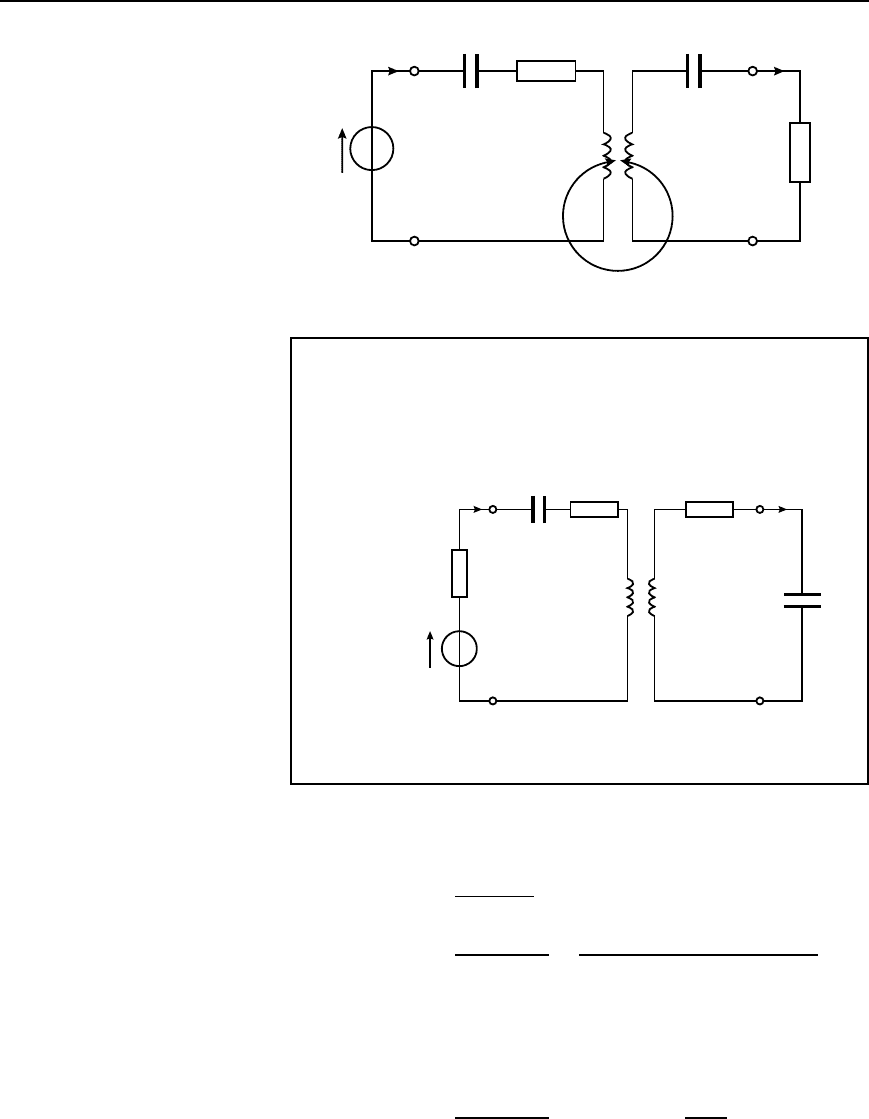
Magnetically coupled circuits 855

Figure 43.11

Problem 12. For the circuit shown in Figure 43.12 each winding

is tuned to resonate at the same frequency. Determine (a) the reso-

nant frequency, (b) the value of capacitor C

, (c) the effective

primary impedance, (d) the primary current, (e) the voltage across

capacitor C

and (f) the coefﬁcient of coupling.

400 pF

30 Ω

1 mH 0.2 mH

50 Ω

15 Ω

M = 10 µH

= 20∠0° V

Figure 43.12

(a) For resonance in a series circuit, the resonant frequency, f

,is

given by:

2

LC

Hence f

2

L



2



1 ð 10

3

400 ð 10

12



D 251.65 kHz

(b) The secondary is also tuned to a resonant frequency of 251.65 kHz.

Hence f

2

L



i.e., 2f



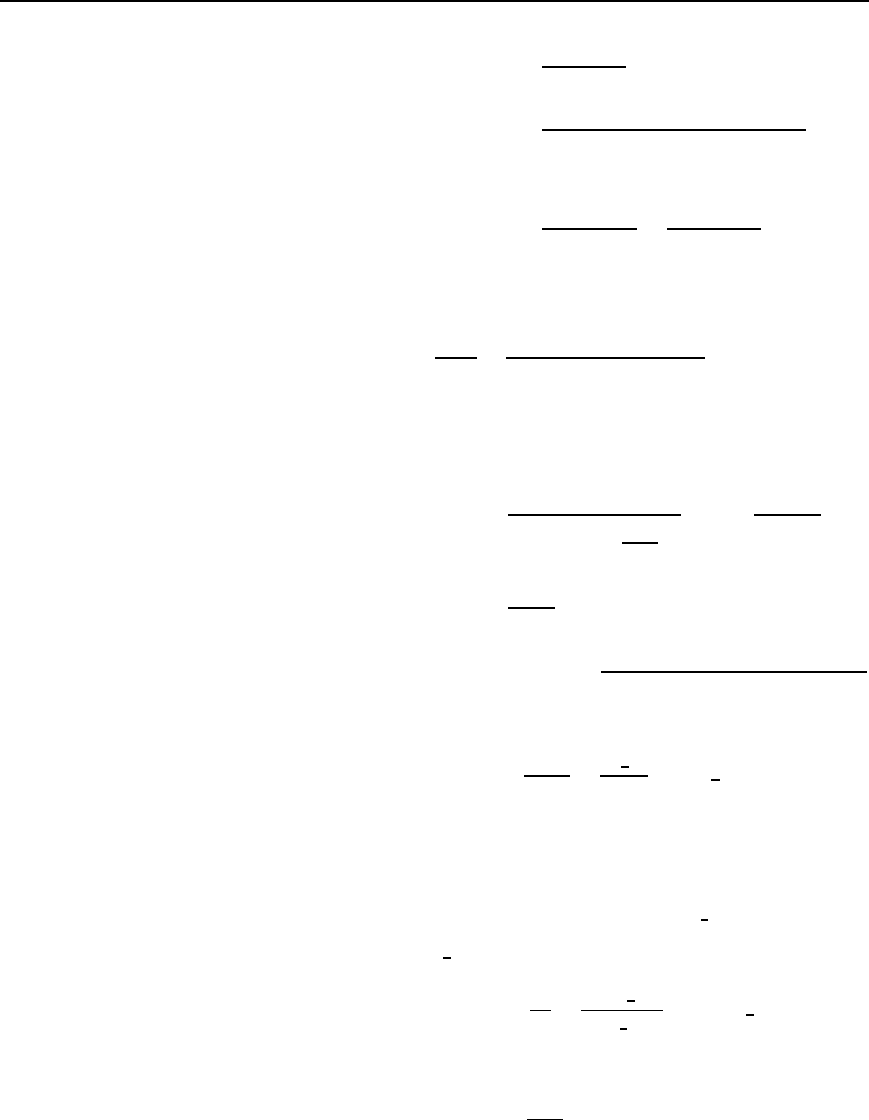
856 Electrical Circuit Theory and Technology

and capacitance, C

2f



0.2 ð 10

3

[2251.65 ð 10

]

D 2.0 ð 10

9

For2.0nF

(Note that since f

2

L



2

L



then L

D L

and C

1 ð 10

3

400 ð 10

12



0.2 ð 10

3

D 2.0 nF)

tive primary impedance Z

1eff

, from equation (43.25) is resistive,

i.e., Z

1.eff/

D R



ωL



ωC



D R

D 15 C 30

[2251.65 ð 10

]

10 ð 10

6



D 45 C 5 D 50 Z

(d) Primary current, I

1eff

D 0.40

(e) From equation (43.18), secondary voltage

D jωMI

D j2251.65 ð 10

10 ð 10

6

0.40



D 6.325

Secondary current, I

6.325

D 0.1265

Hence voltage across capacitor C

D I

X

 D I





ωC



Magnetically coupled circuits 857

D 0.1265





[2251.65 ð 10

]2.0 ð 10

9



90



D 40

(f) From equation (43.10), the

coefﬁcient of coupling, k D

L



10 ð 10

6



1 ð 10

3

0.2 ð 10

3



D 0.0224

Further problem on coupled circuits may be found in Section 43.8,

problems 12 to 16, page 866.

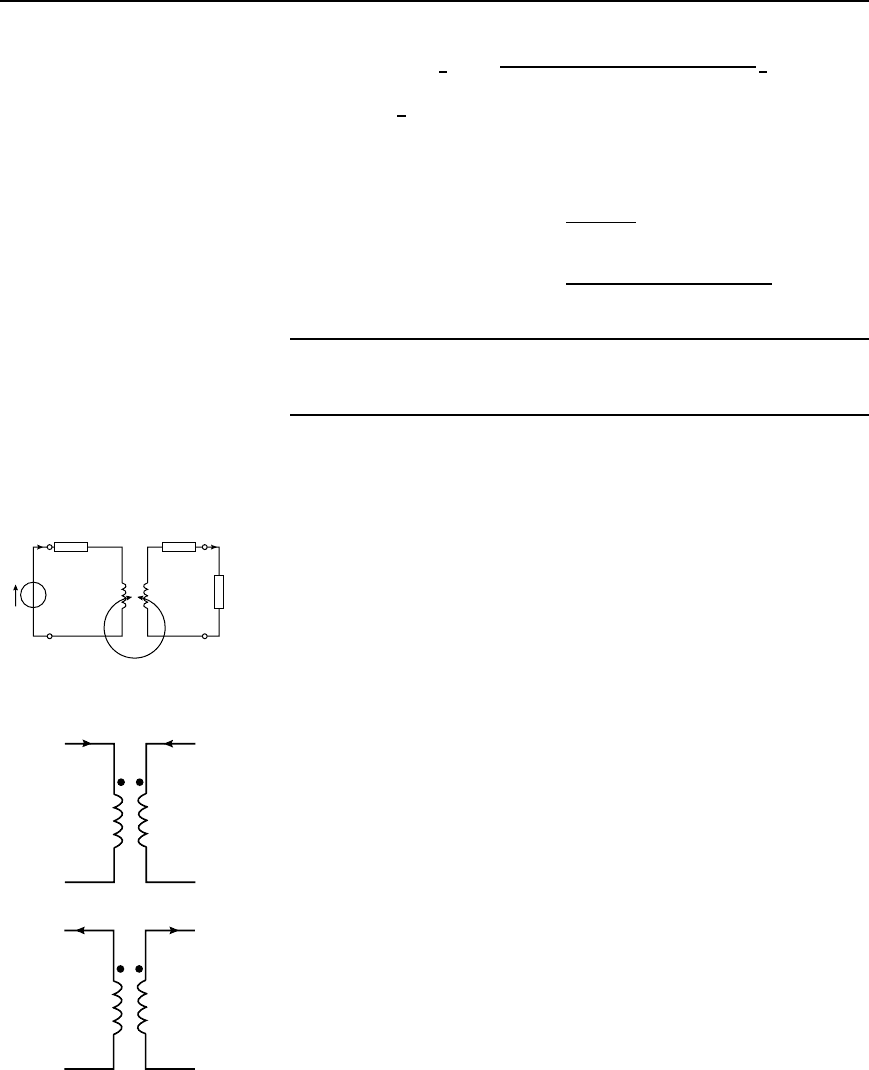
43.7 Dot rule for coupled

circuits

Applying Kirchhoff’s voltage law to each mesh of the circuit shown in

Figure 43.13 gives:

D I

R

C jωL

 š jωMI

and 0 D I

R

C R

C jωL

 š jωMI

In these equations the ‘M’ terms have been written as š because it is

not possible to state whether the magnetomotive forces due to currents

and I

are added or subtracted. To make this clearer a dot nota-

tion is used whereby the polarity of the induced e.m.f. due to mutual

inductance is identiﬁed by placing a dot on the diagram adjacent to that

end of each equivalent winding which bears the same relationship to the

magnetic ﬂux.

Figure 43.13

The dot rule determines the sign of the voltage of mutual inductance

in the Kirchhoff’s law equations shown above, and states:

(i) when both currents enter, or both currents leave, a pair of coupled

coils at the dotted terminals, the signs of the ‘M’ terms will be the

same as the signs of the ‘L’ terms, or

(ii) when one current enters at a dotted terminal and one leaves by a

dotted terminal, the signs of the ‘M’ terms are opposite to the signs

of the ‘L’ terms.

Thus Figure 43.14 shows two cases in which the signs of M and L are

the same, and Figure 43.15 shows two cases where the signs of M and

L are opposite. In Figure 43.13, therefore, if dots had been placed at

the top end of coils L

and L

then the terms jωMI

and jωMI

the Kirchhoff’s equation would be negative (since current directions are

similar to Figure 43.15(a)).

(a)

(b)

Figure 43.14