Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

718 Electrical Circuit Theory and Technology

(d) From equation (39.3), dissipation factor,

D D

D 0.030159 or 0.030, correct to 3 decimal places.

Problem 2. A capacitor has a loss angle of 0.025 rad, and when it

is connected across a 5 kV, 50 Hz supply, the power loss is 20 W.

Determine the component values of the equivalent parallel circuit.

From equation (39.5),

power loss D V

ωC tanυ

i.e., 20 D 5000

250C tan0.025

from which capacitance C D

5000

250 tan0.025

D 0.102 mF

(Note tan0.025 means ‘the tangent of 0.025 rad’)

From equation (39.4), for a parallel equivalent circuit,

tanυ D

ωC

from which, parallel resistance,

ωC

tanυ

2500.102 ð 10

6

 tan0.025

i.e., R

= 1.248 MZ

Problem 3. A 2000 pF capacitor has an alternating voltage of

20 V connected across it at a frequency of 10 kHz. If the power

dissipated in the dielectric is 500

µW, determine (a) the loss angle,

(b) the equivalent series loss resistance, and (c) the equivalent

parallel loss resistance.

(a) From equation (39.5), power loss D V

ωC tanυ, i.e.,

500 ð 10

6

D 20

210 ð 10

2000 ð 10

12

 tanυ

Hence tanυ D

500 ð 10

6

20

210 ð 10

2000 ð 10

12



D 9.947 ð 10

3

from which, loss angle, d = 0.57

or 9.95 × 10

−3

rad.

(b) From equation (39.1), for an equivalent series circuit,

tanυ D R

ωC

, from which equivalent series resistance,

tanυ

ωC

9.947 ð10

3

210 ð 10

2000 ð 10

12



i.e., R

= 79.16 Z

Dielectrics and dielectric loss 719

tanυ D

ωC

from which equivalent parallel resistance,

tan υωC

9.947 ð 10

3

210 ð 10

2000 ð 10

12



i.e., R

= 800 kZ

Further problems on dielectric loss and loss angle may be found in

Section 39.9 following, problems 1 to 5.

39.9 Further problems

on dielectric loss and loss

angle

1 The equivalent series circuit for a capacitor consists of a 3  resistance

in series with a 250 pF capacitor. Determine the loss angle of the

capacitor at a frequency of 5 MHz, giving the answer in degrees and

in radians. Find also for the capacitor, (a) the power factor, (b) the

Q-factor, and (c) the dissipation factor.

[1.35

or 0.024 rad (a) 0.0236 (b) 42.4 (c) 0.0236]

2 A capacitor has a loss angle of 0.008 rad and when it is connected

across a 4 kV, 60 Hz supply the power loss is 15 W. Determine the

component values of (a) the equivalent parallel circuit, and (b) the

equivalent series circuit.

[(a) 0.311

µF, 1.066 M (b) 0.311 µF, 68.24 ]

3 A coaxial cable has a capacitance of 4

µF and a dielectric power loss

of 12 kW when operated at 50 kV and frequency 50 Hz. Calculate

(a) the value of the loss angle, and (b) the equivalent parallel resis-

tance of the cable.

[(a) 0.219

or 3.82 ð 10

3

rad (b) 208.3 k]

4 What are the main reasons for power loss in capacitors with solid

dielectrics? Explain the term ‘loss angle’.

A voltage of 10 V and frequency 20 kHz is connected across a 1 nF

capacitor. If the power dissipated in the dielectric is 0.2 mW, deter-

mine (a) the loss angle, (b) the equivalent series loss resistance, and

[(a) 0.912

or 0.0159 rad (b) 126.7  (c) 0.5 M]

5 The equivalent series circuit for a capacitor consists of a 0.5  resistor

in series with a capacitor of reactance 2 k. Determine for the capac-

itor (a) the loss angle, (b) the power factor, and (c) the equivalent

parallel resistance.

[(a) 0.014

or 2.5 ð 10

4

rad (b) 2.5 ð10

4

40 Field theory

At the end of this chapter you should be able to:

ž understand ﬁeld plotting by curvilinear squares

ž show that the capacitance between concentric cylinders,

C D

2ε

lnb/a

and calculate C given values of radii a and b

ž calculate dielectric stress E D

r lnb/a

ž appreciate dimensions of the most economical cable

ž show that the capacitance of an isolated twin line,

C D

ε

lnD/a

and calculate C given values of a and D

ž calculate energy stored in an electric ﬁeld

ž show that the inductance of a concentric cylinder,

L D



2



C ln



and calculate L given values of a

and b

ž show that the inductance of an isolated twin line,

C D







C ln



and calculate L given values of a

and D

ž calculate energy stored in an electromagnetic ﬁeld

40.1 Field plotting by

curvilinear squares

Electric ﬁelds, magnetic ﬁelds and conduction ﬁelds (i.e., a region in

which an electric current ﬂows) are analogous, i.e., they all exhibit similar

characteristics. Thus they may all be analysed by similar processes. In the

following the electric ﬁeld is analysed

Figure 40.1 shows two parallel plates A and B. Let the potential on

plate A be CV volts and that on plate B be V volts. The force acting on

a point charge of 1 coulomb placed between the plates is the electric ﬁeld

strength E. It is measured in the direction of the ﬁeld and its magnitude

depends on the p.d. between the plates and the distance between the

plates. In Figure 40.1, moving along a line of force from plate B to plate

A means moving from V to CV volts. The p.d. between the plates

is therefore 2 V volts and this potential changes linearly when moving

from one plate to the other. Hence a potential gradient is followed which

changes by equal amounts for each unit of distance moved.

Field theory 721

Figure 40.1 Lines of force intersecting equipotential lines in an electric

ﬁeld

Lines may be drawn connecting together all points within the ﬁeld

having equal potentials. These lines are called equipotential lines and

these have been drawn in Figure 40.1 for potentials of

V, 0,



Vand

V. The zero equipotential line represents earth potential

and the potentials on plates A and B are respectively above and below

earth potential. Equipotential lines form part of an equipotential surface.

Such surfaces are parallel to the plates shown in Figure 40.1 and the

plates themselves are equipotential surfaces. There can be no current ﬂow

between any given points on such a surface since all points on an equipo-

tential surface have the same potential. Thus a line of force (or ﬂux) must

intersect an equipotential surface at right angles. A line of force in an

electrostatic ﬁeld is often termed a streamline.

An electric ﬁeld distribution for a concentric cylinder capacitor is

shown in Figure 40.2. An electric ﬁeld is set up in the insulating medium

between two good conductors. Any volt drop within the conductors can

usually be neglected compared with the p.d.’s across the insulation since

the conductors have a high conductivity. All points on the conductors

are thus at the same potential so that the conductors form the boundary

equipotentials for the electrostatic ﬁeld. Streamlines (or lines of force)

which must cut all equipotentials at right angles leave one boundary

at right angles, pass across the ﬁeld, and enter the other boundary at

right angles.

Figure 40.2 Electric ﬁeld

distribution for a concentric

cylinder capacitor

In a magnetic ﬁeld, a streamline is a line so drawn that its direction is

everywhere parallel to the direction of the magnetic ﬂux. An equipotential

surface in a magnetic ﬁeld is the surface over which a magnetic pole may

be moved without the expenditure of work or energy.

In a conduction ﬁeld, a streamline is a line drawn with a direction

which is everywhere parallel to the direction of the current ﬂow.

A method of solving certain ﬁeld problems by a form of graphical

estimation is available which may only be applied, however, to plane

linear ﬁelds; examples include the ﬁeld existing between parallel plates

or between two long parallel conductors. In general, the plane of a ﬁeld

may be divided into a number of squares formed between the line of

force (i.e. streamline) and the equipotential. Figure 40.3 shows a typical

pattern. In most cases true squares will not exist, since the streamlines and

equipotentials are curved. However, since the streamlines and the equipo-

tentials intersect at right angles, square-like ﬁgures are formed, and these

are usually called ‘curvilinear squares’. The square-like ﬁgure shown

Figure 40.3 Curvilinear

square

722 Electrical Circuit Theory and Technology

in Figure 40.3 is a curvilinear square since, on successive subdivision by

equal numbers of intermediate streamlines and equipotentials, the smaller

ﬁgures are seen to approach a true square form.

When subdividing to give a ﬁeld in detail, and in some cases for the

initial equipotentials, ‘Moores circle’ technique can be useful in that

it tends to eliminate the trial and error process. If, say, two ﬂux lines

and an equipotential are given and it is required to draw a neighbouring

equipotential, a circle tangential to the three given lines is constructed.

The new equipotential is then approximately tangential to the circle, as

shown in Figure 40.3.

Consider the electric ﬁeld established between two parallel metal plates,

as shown in Figure 40.4. The streamlines and the equipotential lines are

shown sketched and are seen to form curvilinear squares. Consider a true

square abcd lying between equipotentials AB and CD. Let this square

be the end of x metres depth of the ﬁeld forming a ﬂux tube between

adjacent equipotential surfaces abfe and cdhg as shown in Figure 40.5.

Let l be the length of side of the squares. Then the capacitance C

of the

ﬂux tube is given by

(area of plate)

plate separation

i.e., C

lx

D "

x 40.1

Thus the capacitance of the ﬂux tube whose end is a true square is inde-

pendent of the size of the square.

Let the distance between the plates of a capacitor be divided into an

exact number of parts, say n (in Figure 40.4, n D 4). Using the same

scale, the breadth of the plate is divided into a number of parts (which is

not always an integer value), say m (in Figure 40.4, m D 10, neglecting

fringing). Thus between equipotentials AB and CD in Figure 40.4 there

are m squares in parallel and so there are m capacitors in parallel. For m

capacitors connected in parallel, the equivalent capacitance C

is given by

D C

C C

CÐÐÐCC

. If the capacitors have the same value,

Figure 40.4 Figure 40.5

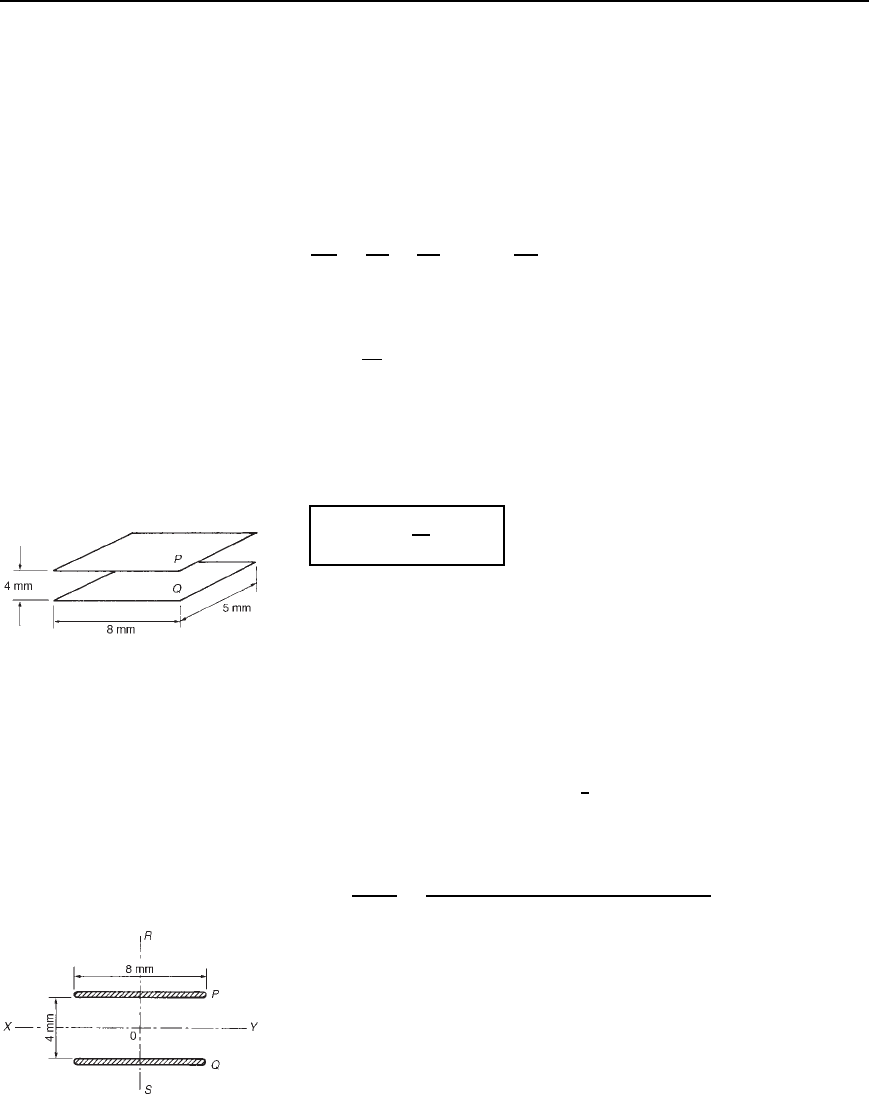
Field theory 723

i.e., C

D C

DÐÐÐDC

D C

, then

D mC

40.2

Similarly, there are n squares in series in Figure 40.4 and thus n capacitors

in series.

For n capacitors connected in series, the equivalent capacitance C

given by

CÐÐÐC

If C

D C

DÐÐÐDC

D C

then 1/C

D n/C

, from which

40.3

Thus if m is the number of parallel squares measured along each

equipotential and n is the number of series squares measured along each

streamline (or line of force), then the total capacitance C of the ﬁeld is

given, from equations (40.1)–(40.3), by

C = "

farads

40.4

For example, let a parallel-plate capacitor have plates 8 mm ð 5mmand

spaced 4 mm apart (See Figure 40.6). Let the dielectric have a relative

permittivity 3.5. If the distance between the plates is divided into, say,

four equipotential lines, then each is 1 mm apart. Hence n D 4.

Figure 40.6

Using the same scale, the number of lines of force from plate P to

plate Q must be 8, i.e. m D 8. This is, of course, neglecting any fringing.

From equation (40.4), capacitance C D ε

xm/n, where x D 5mmor

0.005 m in this case. Hence

C D 8.85 ð 10

12

3.50.005





D 0.31 pF

(Using the normal equation for capacitance of a parallel-plate capacitor,

C D

8.85 ð 10

12

3.50.008 ð 0.005

0.004

D 0.31 pF

The capacitance found by each method gives the same value; this is

expected since the ﬁeld is uniform between the plates, giving a ﬁeld plot

of true squares.)

The effect of fringing may be considered by estimating the capacitance

by ﬁeld plotting. This is described below.

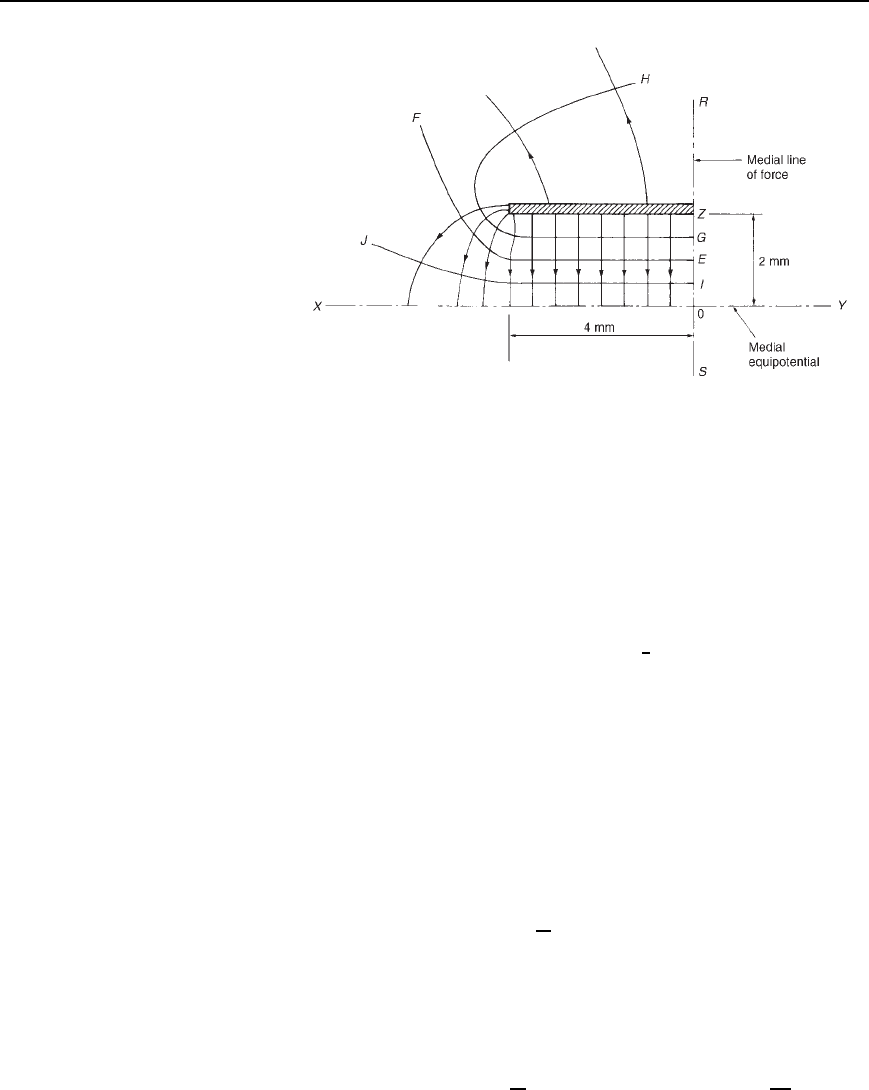
In the side view of the plates shown in Figure 40.7, RS is the medial

line of force or medial streamline, by symmetry. Also XY is the medial

equipotential. The ﬁeld may thus be divided into four separate symmet-

rical parts.

Figure 40.7

724 Electrical Circuit Theory and Technology

Figure 40.8

Considering just the top left part of the ﬁeld, the ﬁeld plot is estimated

as follows, with reference to Figure 40.8:

(i) Estimate the position of the equipotential EF which has the

mean potential between that of the plate and that of the medial

equipotential XO. F is not taken too far since it is difﬁcult to

estimate. Point E will lie slightly closer to point Z than point O.

(ii) Estimate the positions of intermediate equipotentials GH and IJ.

(iii) All the equipotential lines plotted are

, i.e., 0.5 mm apart. Thus a

series of streamlines, cutting the equipotential at right angles, are

drawn, the streamlines being spaced 0.5 mm apart, with the object

of forming, as far as possible, curvilinear squares.

It may be necessary to erase the equipotentials and redraw them to ﬁt the

lines of force. The ﬁeld between the plates is almost uniform, giving a

ﬁeld plot of true squares in this region. At the corner of the plates the

squares are smaller, this indicating a great stress in this region.

On the top of the plate the squares become very large, indicating that

the main ﬁeld exists between the plates.

From equation (40.4),

total capacitance, C D ε

farads

The number of parallel squares measured along each equipotential is about

13 in this case and the number of series squares measured along each line

of force is 4. Thus, for the plates shown in Figure 40.7, m D 2 ð 13 D 26

and n D 2 ð 4 D 8. Since x is 5 mm,

total capacitance D ε

D 8.85 ð 10

12

3.50.005

D 0.50 pF

Field theory 725

Figure 40.9

Problem 1. A ﬁeld plot between two metal plates is shown in

Figure 40.9. The relative permeability of the dielectric is 2.8.

Determine the capacitance per metre length of the system.

From equation (40.4), capacitance C D ε

xm/n. From Figure 40.9,

m D 16, i.e., the number of parallel squares measured along each

equipotential, and n D 6, i.e., the number of series squares measured

along each line of force. Hence capacitance fo

ra1mlength,

C D 8.85 ð 10

12

2.81

D 66.08 pF

Problem 2. A ﬁeld plot for a cross-section of a concentric cable is

shown in Figure 40.10. If the relative permeability of the dielectric

is 3.4, determine the capacitance of a 100 m length of the cable.

Figure 40.10

From equation (40.4), capacitance C D ε

xm/n. In this case, m D 13

and n D 4. Also x D 100 m. Thus

capacitance C D 8.85 ð10

12

3.4100

D 9780 pF or 9.78 nF

Further problems on ﬁeld plotting by curvilinear squares may be found in

Section 40.9, problems 1 to 3, page 753.

40.2 Capacitance

between concentric

cylinders

A concentric cable is one which contains two or more separate

conductors, arranged concentrically (i.e., having a common centre), with

insulation between them. In a coaxial cable, the central conductor,

which may be either solid or hollow, is surrounded by an outer tubular

conductor, the space in between being occupied by a dielectric. If air

is the dielectric then concentric insulating discs are used to prevent the

conductors touching each other. The two kinds of cable serve different

purposes. The main feature they have in common is a complete absence

of external ﬂux and therefore a complete absence of interference with and

from other circuits.

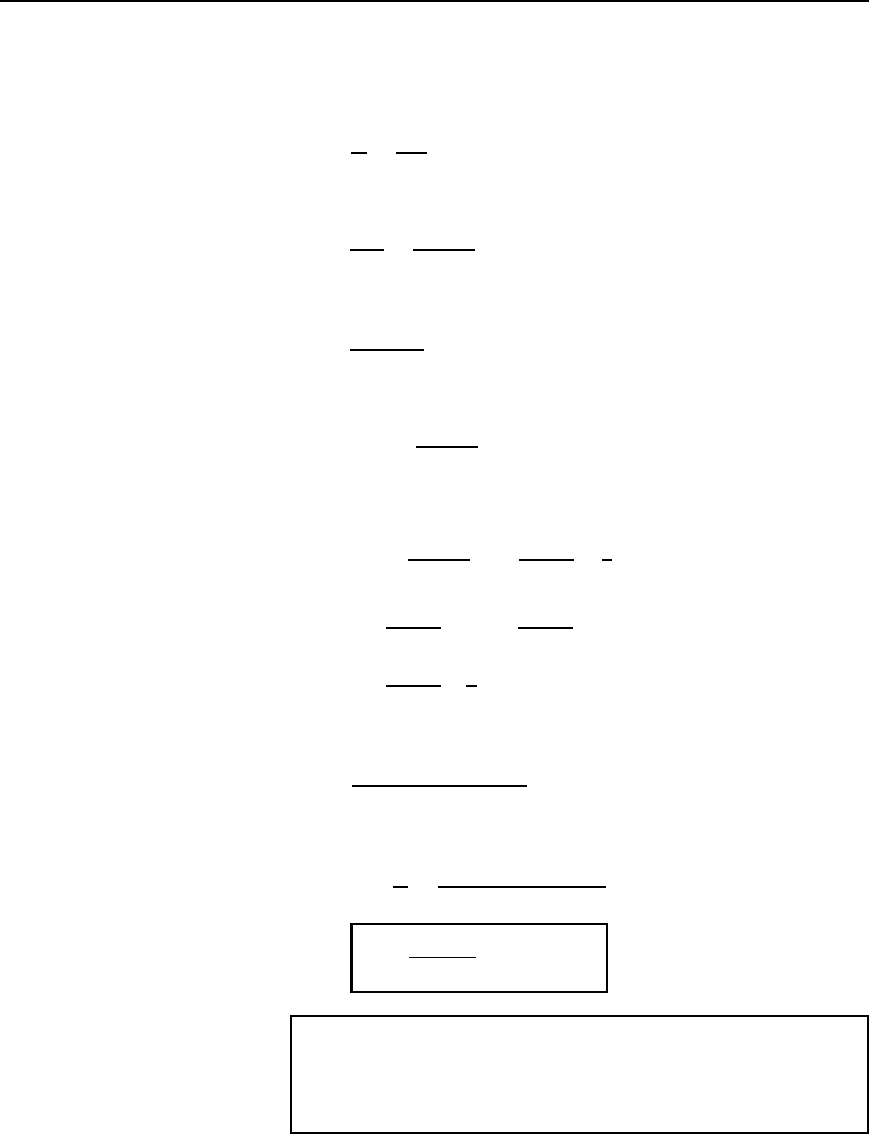
The electric ﬁeld between two concentric cylinders (i.e., a coaxial

cable) is shown in the cross-section of Figure 40.11. The conductors form

the boundary equipotentials for the ﬁeld, the boundary equipotentials in

Figure 40.11 being concentric cylinders of radii a and b. The streamlines,

or lines of force, are radial lines cutting the equipotentials at right angles.

Let Q be the charge per unit length of the inner conductor. Then the

total ﬂux across the dielectric per unit length is Q coulombs/metre. This

total ﬂux will pass through the elemental cylinder of width υr at radius r

(shown in Figure 40.11) and a distance of 1 m into the plane of the

paper.

Inner

conductor

δr

Streamlines

Equipotential

Outer

conductor

Figure 40.11 Electric ﬁeld

between two concentric cylinders

726 Electrical Circuit Theory and Technology

The surface area of a cylinder of lengt

h1mwithin the dielectric with

radius r is 2r ð 1 m

Hence the electric ﬂux density at radius r,

D D

2r

The electric ﬁeld strength or electric stress E, at radius r is given by

E D

2rε

volts/metre 40.5

Let the p.d. across the element be υV volts. Since

E D

voltage

thickness

voltage D E ð thickness. Therefore

υV D Eυr D

2rε

υr

The total p.d. between the boundaries,

V D



2rε

dr D

2ε



2ε

[lnr]

2ε

[lnb  ln a]

i.e., V D

2ε

volts 40.6

The capacitance per unit length,

C D

charge per unit length

p.d.

Hence capacitance,

C D

Q/2ε

 lnb/a

i.e.,

C =

2p"

ln.b=a/

farads=metre

40.7

Problem 3. A coaxial cable has an inner core radius of 0.5 mm

and an outer conductor of internal radius 6.0 mm. Determine the

capacitance per metre length of the cable if the dielectric has a

relative permittivity of 2.7.

Field theory 727

From equation (40.7),

capacitance C D

2ε

lnb/a

28.85 ð 10

12

2.7

ln6.0/0.5

D 60.4pF

Problem 4. A single-core concentric cable has a capacitance of

80 pF per metre length. The relative permittivity of the dielectric

is 3.5 and the core diameter is 8.0 mm. Determine the internal

diameter of the sheath.

From equation (40.7), capacitance

C D

2ε

lnb/a

F/m

from which ln

2ε

28.85 ð 10

12

3.5

80 ð 10

12



D 2.433

Since the core radius, a D 8.0/2 D 4.0 mm, lnb/4.0 D 2.433 and

b/4.0 D e

2.433

Thus the internal radius of the sheath, b D 4.0e

2.433

D 45.57 mm. Hence

the internal diameter of the sheath 2 ð 45.57 D 91.14 mm.

Dielectric stress

Rearranging equation (40.6) gives:

2ε

lnb/a

However, from equation (40.5),

E D

2rε

Thus dielectric stress,

E =

r ln.b=a/

volts=metre

40.8

From equation (40.8), the dielectric stress at any point is seen to be

inversely proportional to r, i.e., E / 1/r.

The dielectric stress E will have a maximum value when r is at its

minimum, i.e., when r D a. Thus

max

a ln.b=a/

40.9