Bichop R.H. (Ed.) Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling
Подождите немного. Документ загружается.


16-8 Mechatronic Systems, Sensors, and Actuators
Electrical capacitors, for instance, may be combined in parallel or in series and the resulting equivalent
capacitor may readily be determined. In a parallel connection, equilibrium is determined by voltage (an
intensive variable) and the electric charges (extensive variables) are added as before. However, a series
connection is the “dual” in the sense that the roles of charge and voltage are exchanged: equality of charges
determines equilibrium and the voltages are added. Mechanical springs may also be combined in two ways.
However, that is not the case for translational masses and rotational inertias; they may only be combined
into a single equivalent rigid body if their velocities are equal and in that case their momenta are added.
The existence of two “dual” ways to combine some, but not all, of the energy storage elements based
on nonscalar quantities is somewhat confusing. It may have contributed to the lengthy debate (if we date
its beginning to Maxwell, lasting for over a century!) on the best analogy between mechanical and electrical
systems. Nevertheless, the important point is that series and parallel connections may not be generalized
in a straightforward way to all domains.
16.5.4 Nodicity
As insight is the foremost goal of modeling, analogies should be chosen to promote insight. Because there
may be fundamental differences between all of the physical domains, care should be exercised in drawing
analogies to ensure that special properties of one domain should not be applied inappropriately to other
domains. This brings us to what may well be the strongest argument against the across-through classification.
History suggests that it originated with the use of equivalent electrical network representations of nonelec-
trical systems. Unfortunately, electrical networks provide an inappropriate basis for developing a general
representation of physical system dynamics. This is because electrical networks enjoy a special property,
nodicity, which is quite unusual among the physical system domains (except as an approximation).
Nodicity refers to the fact that any sub-network (cut-set) of an electrical network behaves as a node
in the sense that a Kirchhoff current balance equation may be written for the entire sub-network. As a
result of nodicity, electrical network elements can be assembled in arbitrary topologies and yet still
describe a physically realizable electrical network. This property of “arbitrary connectability” is not a
general property of lumped-parameter physical system models. Most notably, mass elements cannot be
connected arbitrarily; they must always be referenced to an inertial frame. For that reason, electrical
networks can be quite misleading when used as a basis for a general representation of physical system
dynamics. This is not merely a mathematical nicety; some consequences of non-nodic behavior for control
system analysis have recently been explored (Won and Hogan, 1998).
By extension, because each of the physical domains has its unique characteristics, any attempt to
formulate analogies by taking one of the domains (electrical, mechanical, or otherwise) as a starting point
is likely to have limitations. A more productive approach is to begin with those characteristics of physical
variables common to all domains and that is the reason to turn to thermodynamics. In other words, the
best way to identify analogies between domains may be to “step outside” all of them. By design, general
characteristics of all domains such as the extensive nature of stored energy, the intensive nature of the
variables that define equilibrium, and so forth, are not subject to the limitations of any one (such as
nodicity). That is the main advantage of drawing analogies based on thermodynamic concepts such as
the distinction between extensive and intensive variables.
16.6 Graphical Representations
Analogies are often associated with abstract graphical representations of multi-domain physical system
models. The force-current analogy is usually associated with the linear graph representation of networks
introduced by Trent (1955); the force-voltage analogy is usually associated with the bond graph represen-
tation introduced by Paynter (1960). Bond graphs classify variables into efforts (commonly force, voltage,
pressure, and so forth) and flows (commonly velocity, current, fluid flow rate, and so forth). Bond graphs
extend all the practical benefits of the force-current (across-through) analogy to the force-voltage (effort-
flow) analogy: they provide a unified representation of lumped-parameter dynamic behavior in several
9258_C016.fm Page 8 Tuesday, October 2, 2007 1:22 AM

The Physical Basis of Analogies in Physical System Models 16-9
domains that has been expounded in a number of successful textbooks (e.g., Karnopp et al., 1975,
1999), there are systematic methods for selecting sets of independent variables to describe a system,
ways to take advantage of the ease of identifying velocities and voltages, and matrix methods to facilitate
computer analysis. In fact, several computer-aided modeling support packages using the bond-graph
language are now available. Furthermore, bond graphs have been applied successfully to describe the
dynamics of spatial mechanisms (including gyroscopic effects) while, to the authors’ knowledge, linear
graphs have not.
Although the force–voltage analogy is most commonly used with bond graphs, the force–current
analogy can be used just as readily; the underlying mathematical formalism is indifferent to the choice
of which variables are chosen as analogous. In fact, pursuing this line of thought, the choice is unnecessary
and may be avoided; doing so affords a way to clarify the potential confusion over the role of intensive
variables and the dual types of connection available for some elements in some domains.
In the Generalized Bond Graph (GBG) approach (Breedveld, 1984) all energy storage becomes anal-
ogous and only one type of storage element, a (generalized) capacitor, is identified. Its displacement is
an extensive variable; the gradient of its energy storage function with respect to that displacement is an
intensive variable. In some (but not all) domains a particular kind of coupling known as a gyrator is
found that gives rise to the appearance of a dual type of energy storage, a (generalized) inertia as well as
the possibility of dual ways to connect elements. The GBG representation emphasizes the point that the
presence of dual types of energy storage and dual types of connection is a special property (albeit an
important one) of a limited number of domains. In principle, either a “mass–capacitor” analogy or a
“mass–inductor” analogy can be derived from a GBG representation by choosing to associate the gyrating
coupling with either the “equilibrium” or “steady-state” energy storage elements.
The important point to be taken here is that the basis of analogies between domains does not depend
on the use of a particular abstract graphical representation. The practical value of establishing analogies
between domains and the merits of a domain-independent approach based on intensive versus extensive
variables remains regardless of which graph-theoretic tools (if any) are used for analysis.
16.7 Concluding Remarks
In the foregoing we articulated some important considerations in the choice of analogies between
variables in different physical domains. From a strictly mathematical viewpoint there is little to choose;
both analogies may be used as a basis for rigorous, self-consistent descriptions of physical systems. The
substantive and important factors emerge from a physical viewpoint—considering the structured way
physical behavior is described in the different domains. Summarizing:
•
The “system-of-particles” model that is widely assumed in basic science and engineering naturally
leads to the intuitive analogy between force and voltage, velocity and current, a mass and an
inductor, and so on.
•
The measurement procedures used to motivate the distinction between across and through vari-
ables at best yield an ambiguous classification.
•
Nodicity (the property of “arbitrary connectability”) is not a general property of lumped-
parameter physical system models. Thus, electrical networks, which are nodic, can be quite
misleading when used as a basis for a general representation of physical system dynamics.
•
The intuitive analogy between velocity and current is consistent with a thermodynamic classifi-
cation into extensive and intensive variables. As a result, the analogy can be generalized to dynamic
behavior in domains to which the “system-of-particles” image may be less applicable.
•
The force–voltage or mass-inductor analogy reflects an important distinction between equilibrium
energy-storage phenomena and steady-state energy-storage phenomena: the constitutive equations
of steady-state energy storage phenomena require an inertial reference frame (or must be modified
in a non-inertial reference frame) while the constitutive equations of equilibrium energy storage
phenomena do not.
9258_C016.fm Page 9 Tuesday, October 2, 2007 1:22 AM
16-10 Mechatronic Systems, Sensors, and Actuators
Our reasoning is based on an assumption that models of physical system dynamics should properly
reflect the way descriptions of physical phenomena depend on reference frames and should be compatible
with thermodynamics. The across-through classification of variables does not meet these requirements.
By contrast, the classification of variables based on the system-of-particles point of view that leads to an
analogy between force, pressure, and voltage on the one hand and velocity, fluid flow, and current on
the other not only satisfies these criteria, but is the least artificial from a common-sense point of view.
We believe this facilitates communication and promotes insight, which are the ultimate benefits of using
analogies.
Acknowledgments
Neville Hogan was supported in part by grant number AR40029 from the National Institutes of Health.
References
(1926). Models and analogies for demonstrating electrical principles, parts I-XIX. The Engineer, 142.
Breedveld, P.C. (1984). Physical Systems Theory in Terms of Bond Graphs, University of Twente, Enschede,
Netherlands, ISBN 90-9000599-4 (distr. by author).
Darrieus, M. (1929). Les modeles mecaniques en electrotechnique. Leur application aux problemes de
stabilite. Bull. Soc. Franc. Electric., 36:729–809.
Feynman, R.P., Leighton, R.B., and Sands, M. (1963). The Feynman Lectures on Physics, Volume II: Mainly
Electromagnetism and Matter, Addison-Wesley Publishing Company.
Firestone, F.A. (1933). A new analogy between mechanical and electrical system elements. Journal of the
Acoustic Society of America, 3:249–267.
Hähnle, W. (1932). Die darstellung elektromechanischer gebilde durch rein elektrsiche schaltbilder.
Wissenschaftliche Veroffentl. Siemens Konzern, 11:1–23.
Karnopp, D.C. and Rosenberg, R.C. (1975). System Dynamics: A Unified Approach, John Wiley.
Karnopp, D.C., Margolis, D.L., and Rosenberg, R.C. (1999). System Dynamics: Modeling and Simulation
of Mechatronic Systems, 3rd ed., John Wiley & Sons
Maxwell, J.C. (1873). Treatise on Electricity and Magnetism.
Nickle, C.A. (1925). Oscillographic solutions of electro-mechanical systems. Trans. A.I.E.E., 44:844–856.
Rowell, D. and Wormley, D.N. (1997). System Dynamics: An Introduction, Prentice-Hall, New Jersey.
Shearer, J.L., Murphy, A.T., and Richardson, H.H. (1967). Introduction to System Dynamics, Addison-
Wesley Publishi ng Compa ny.
Trent, H.M. (1955). Isomorphisms between oriented linear graphs and lumped physical systems. Journal
of the Acoustic Society of America, 27:500–527.
Won, J. and Hogan, N. (1998). Coupled stability of non-nodic physical systems. IFAC Symposium on
Nonlinear Control Systems Design.
Yazdi, N., Ayazi, F., and Najafi, K. (1998). Micromachined inertial sensors. Proc. IEEE, 86(8), 1640–1659.
9258_C016.fm Page 10 Tuesday, October 2, 2007 1:22 AM

III
Mechatronic Sensors
and Actuators
17 Introduction to Sensors and Actuators
M. Anjanappa, K. Datta, T. Song, Raghavendra Angara, and S. Li ....................................... 17-1
Introduction
18 Fundamentals of Time and Frequency
Michael A. Lombardi ................................................................................................................. 18-1
Introduction
•
Time and Frequency Measurement
•
Time and Frequency Standards
•
Time and Frequency Transfer • Closing
19 Sensor and Actuator Characteristics
Joey Parker ................................................................................................................................. 19-1
Range
•
Resolution
•
Sensitivity
•
Error
•
Repeatability
•
Linearity and Accuracy
Impedance
•
Nonlinearities
•
Static and Coulomb Friction
•
Eccentricity
•
Backlash
Saturation
•
Deadband
•
System Response
•
First-Order System Response
Underdamped Second-Order System Response
•
Frequency Response
20 Sensors
Kevin M. Lynch, Michael A. Peshkin, Halit Eren, M. A. Elbestawi, Ivan J. Garshelis,
Richard Thorn, Pamela M. Norris, Bouvard Hosticka, Jorge Fernando Figueroa,
H. R. (Bart)Everett, Stanley S. Ipson, Chang Liu, Nicolas Vazquez, and Dinesh Nair
......... 20-1
Linear and Rotational Sensors
•
Acceleration Sensors
•
Force Measurement
•
To rq u e an d
Power Measurement
•
Flow Measurement
•
Temperature Measurements
•
Distance
Measuring and Proximity Sensors
•
Light Detection, Image, and Vision Systems
•
Integrated Microsensors
•
Vision
21 Actuators
George T.-C. Chiu, Charles J. Fraser, Habil Ramutis Bansevicius, Rymantas Tadas Tolocka,
Massimo Sorli, Stefano Pastorelli, and Sergey Edward Lyshevski
......................................... 21-1
Electromechanical Actuators
•
Electrical Machines
•
Piezoelectric Actuators
•
Hydraulic
and Pneumatic Actuation Systems
•
MEMS: Microtransducers Analysis, Design, and
Fabrication
9258_S003.fm Page 1 Saturday, October 13, 2007 4:15 PM
9258_S003.fm Page 2 Saturday, October 13, 2007 4:15 PM

17-1
17
Introduction to
Sensors and Actuators
17.1 Introduction ................................................................. 17-1
Sensors
•
Actuators
17.1 Introduction
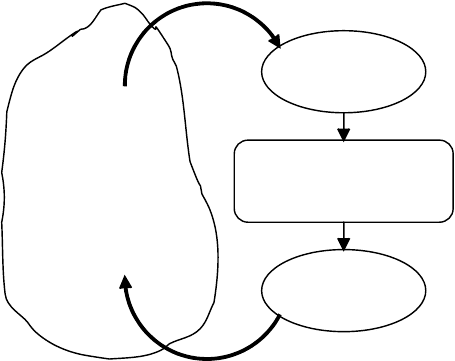
Sensors and actuators are two critical components of every closed loop control system. Such a system is
also called a mechatronics system. A typical mechatronics system as shown in Figure 17.1 consists of a
sensing unit, a controller, and an actuating unit. Sensing unit can be as simple as a single sensor or can
consist of additional components such as filters, amplifiers, modulators, and other signal conditioners.
The controller accepts the information from the sensing unit, makes decisions on the basis of the control
algorithm, and outputs commands to the actuating unit. The actuating unit consists of an actuator and
optionally a power supply and a coupling mechanism.
17.1.1 Sensors
Sensor is a device that when exposed to a physical phenomenon (temperature, displacement, force, etc.)
produces a proportional output signal (electrical, mechanical, magnetic, etc.). The term transducer is
often used synonymously with sensors. However, ideally, a sensor is a device that responds to a change
in the physical phenomenon. On the other hand, a transducer is a device that converts one form of
energy into another form of energy. Sensors are transducers when they sense one form of energy input
and output in a different form of energy. For example, a thermocouple responds to a temperature change
(thermal energy) and outputs a proportional change in electromotive force (electrical energy). Therefore,
a thermocouple can be called as a sensor and or a transducer.
M. Anjanappa
K. Datta
T. Song
Raghavendra Angara
S. Li
University of Maryland Baltimore
County
N9258-17.fm Page 1 Thursday, October 4, 2007 9:44 PM
17-2 Mechatronic Systems, Sensors, and Actuators
17.1.1.1 Classification
Table 17.1 lists various types of sensors that are classified by their measurement objectives. Although this
list is by no means exhaustive, it covers all the basic types including the new generation sensors such as
smart material sensors, microsensors, and nanosensors.
Sensors can also be classified as
passive
or
active
. In passive sensors, the power required to produce the
output is provided by the sensed physical phenomenon itself (such as a thermometer), whereas the active
sensors require external power source (such as a strain gauge).
Furthermore, sensors are classified as analog or digital on the basis of the type of output signal. Analog
sensors produce continuous signals that are proportional to the sensed parameter and typically require
analog to digital conversion before feeding to the digital controller. Digital sensors on the other hand
produce digital outputs that can be directly interfaced with the digital controller. Often, the digital outputs
are produced by adding an analog to digital converter to the sensing unit. If many sensors are required,
it is more economical to choose simple analog sensors and interface them to the digital controller
equipped with a multichannel analog to digital converter.
17.1.1.2 Principle of Operation
Linear and Rotational Sensors: Linear and rotational position sensors are two of the most fundamental
of all measurements used in a typical mechatronics system. The most common type position sensors are
listed in Table 17.1. In general, the position sensors produce an electrical output that is proportional to
the displacement they experience. There are contact type sensors such as strain gauge, LVDT, RVDT,
tachometer, and so forth. The noncontact type includes encoders, Hall effect, capacitance, inductance,
and interferometer type. They can also be classified on the basis of the range of measurement. Usually,
the high-resolution type of sensors such as Hall effect, fiber optic inductance, capacitance, and strain gauge
are suitable for only very small range (typically from 0.1 to 5 mm). The differential transformers, on the
other hand, have a much larger range with good resolution. Interferometer type sensors provide both
very high resolution (in terms of microns) and large range of measurements (typically up to a meter).
However, interferometer type of sensors is bulky, expensive, and requires large setup time.
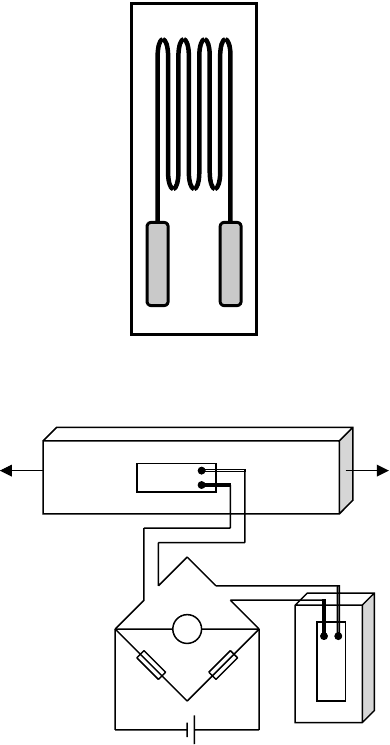
Among many linear displacement sensors, strain gauge provides high resolution at low noise level and is
least expensive. A typical resistance strain gauge consists of resistive foil arranged as shown in Figure 17.2.
A typical setup to measure the normal strain of a member loaded in tension is shown in Figure 17.3.
Strain gauge #1 is bonded to the loading member, whereas strain gauge #2 is bonded to a second member
made of same material, but not loaded. This arrangement compensates for any temperature effect. When
FIGURE 17.1 A typical mechatronics system.
Controlled
system
Sensing
unit
Actuating
unit
Controller
N9258-17.fm Page 2 Thursday, October 4, 2007 9:44 PM

Introduction to Sensors and Actuators 17-3
N9258-17.fm Page 3 Thursday, October 4, 2007 9:44 PM

17-4 Mechatronic Systems, Sensors, and Actuators
the member is loaded, the gauge #1 elongates thereby changing the resistance of the gauge. The change in
resistance is transformed into a change in voltage by the voltage-sensitive Wheatstone bridge circuit. Assum-
ing that the resistance of all four arms are equal initially, the change in output voltage (
⌬
o
) due to change
in resistance (
⌬
R
1
) of gauge #1 is
Acceleration Sensors
: Measurement of acceleration is important for systems subject to shock and vibra-
tion. Although acceleration can be derived from the time history data obtainable from linear or rotary
sensors, the accelerometer whose output is directly proportional to the acceleration is preferred. Two
N9258-17.fm Page 4 Thursday, October 4, 2007 9:44 PM
Introduction to Sensors and Actuators 17-5
common types include the
seismic mass
type and the
piezoelectric
accelerometer. The seismic mass type
accelerometer is based on the relative motion between a mass and the supporting structure. The natural
frequency of the seismic mass limits its use to low to medium frequency applications. The piezoelectric
accelerometer, however, is compact and more suitable for high-frequency applications.
Force, Torque, and Pressure Sensors: Among many type of force/torque sensors, the strain gauge dynamo-
meters and piezoelectric type are most common. Both are available to measure force and/or torque, either
in one axis or multiple axes. The dynamometers make use of mechanical members that experience elastic
deflection when loaded. These types of sensors are limited by their natural frequency. On the other hand,
the piezoelectric sensors are particularly suitable for dynamic loadings in wide range of frequencies. They
provide high stiffness, high resolution over a wide measurement range, and are compact.
Flow Sensors
: Flow sensing is relatively a difficult task. The fluid medium can be liquid, gas, or a mixture
of the two. Furthermore, the flow could be laminar or turbulent and can be a time-varying phenomenon.
The
venturi meter
and
orifice plate
restrict the flow and use the pressure difference to determine the flow
rate. The
pitot tube
pressure probe is another popular method of measuring flow rate. When positioned
against the flow, they measure the total and static pressures. The flow velocity and in turn the flow rate
can then be determined. The
rotameter
and the
turbine meters
when placed in the flow path, rotate at a
FIGURE 17.2 Bonded strain gauge.
FIGURE 17.3 Experimental setup to measure normal strain using strain gauges.
R
R
v
o
v
i
2
1
N9258-17.fm Page 5 Thursday, October 4, 2007 9:44 PM
