Bichop R.H. (Ed.) Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling
Подождите немного. Документ загружается.

15-14 Mechatronic Systems, Sensors, and Actuators
where i is the current in the phase microwinding (supplied by the IC), R
in st
is the inner stator radius, L
is the inductance, P is the number of poles, and g
e
is the equivalent gap, which includes the airgap and
radial thickness of the permanent magnet.
Denoting the number of turns per phase as N
S
, the magnetomotive force is
The simplified expression for the electromagnetic torque for radial topology brushless micromachines is
where B
ag
is the air gap flux density, B
ag
= (
µ
iN
S
/2Pg
e
)cosP
θ
r
, i
s
is the total current, L
r
is the active length
(rotor axial length), and D
r
is the outside rotor diameter.
The axial topology brushless micromachines can be designed and fabricated. The electromagnetic
torque is given as
where k
ax
is the nonlinear coefficient, which is found in terms of active conductors and thin-film permanent
magnet length; and D
a
is the equivalent diameter, which is a function of windings and permanent-magnet
topography.
Example 15.5.1: Mathematical Model of the Translational
Microtransducer
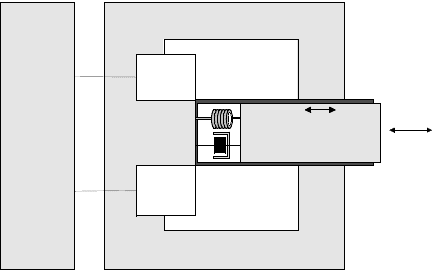
Figure 15.6 illustrates a simple translational microstructure with a stationary member and movable
translational microstructure (plunger), which can be fabricated using continuous batch-fabrication
process [2]. The winding can be ‘‘printed” using the micromachining/CMOS technology.
We apply Newton’s second law of motion to study the dynamics. Newton’s law states that the accel-
eration of an object is proportional to the net force. The vector sum of all forces is found as
FIGURE 15.6 Microtransducer schematics with translational motion microstructure.
mmf
iN
S
P
--------
P
θ
r
cos=
T
1
2
--
PB
ag
i
s
N
S
L
r
D
r
=
Tk
ax
B
ag
i
s
N
S
D
a
2
=
Ft() m
d
2
x
dt
2
--------
B
v
dx
dt
------
+= k
s1
xk
s2
x
2
+()F
e
t()++
Translational motion
microstructure:
plunger
u
a
(t)
Spring, k
s
Damper, B
v
Magnetic force, F
e
(t)
ICs
Winding
Winding
x(t)
9258_C015.fm Page 14 Tuesday, October 2, 2007 3:35 AM
Rotational and Translational Microelectromechanical Systems 15-15
where
x
is the displacement of a translational microstructure (plunger),
m
is the mass of a movable
plunger,
B
v
is the viscous friction coefficient,
k
s
1
and
k
s
2
are the spring constants (the spring can be made
from polysilicon), and
F
e
(
t
) is the magnetic force which is found using the coenergy
W
c
,
F
e
(
i
,
x
)
=
.
The stretch and restoring forces are not directly proportional to the displacement, and these forces
are different on either side of the equilibrium position. The restoring/stretching force exerted by the
polysilicon spring is expressed as (k
s1
x + k
s2
x
2
).
Assuming that the magnetic system is linear, the coenergy is expressed as
Then
The inductance is found as
where ℜ
f
and ℜ
g
are the reluctances of the ferromagnetic material and air gap, A
f
and A
g
are the associated
cross section areas, and l
f
and (x + 2d) are the lengths of the magnetic material and the air gap.
Hence
Using Kirchhoff’s law, the voltage equation for the phase microcircuitry is
where the flux linkage
ψ
is expressed as
ψ
= L(x)i.
One obtains
and thus
Augmenting this equation with differential equation
∂
W
c
i, x()
∂
x
-----------------------
W
c
i, x()
1
2
--
Lx()i
2
=
F
e
i, x()
1
2
--
i
2
dL x()
dx
--------------
=
Lx()
N
2
ℜ
f
ℜ
g
+
------------------
N
2
µ
f
µ
0
A
f
A
g
A
g
l
f
2A
f
µ
f
x 2d+()+
--------------------------------------------------
==
dL
dx
------
2N
2
µ
f
2
µ
0
A
f
2
A
g
A
g
l
f
2A
f
µ
f
x 2d+()+[]
2
---------------------------------------------------------–=
u
a
ri
d
ψ
dt
-------
+=
u
a
ri L x()
di
dt
-----
i
dL x()
dx
--------------
++=
dx
dt
------
di
dt
-----
r
Lx()
-----------
i–
2N
2
µ
f
2
µ
0
A
f
2
A
g
Lx()A
g
l
f
2A
f
µ
f
+ x 2d+()[]
2
--------------------------------------------------------------------
iv
1
Lx()
-----------
u
a
++=
Ft() m
d
2
x
dt
2
--------
B
v
dx
dt
------
k
s1
xk
s2
x
2
+()F
e
t()++ +=
9258_C015.fm Page 15 Tuesday, October 2, 2007 3:35 AM

15-16 Mechatronic Systems, Sensors, and Actuators
three nonlinear differential equations for the studied translation microdevise are found as
Example 15.5.2: Mathematical Model of an Elementary Synchronous
Reluctance Micromotor
Consider a single-phase reluctance micromotor, which can be straightforwardly fabricated using con-
ventional CMOS, LIGA, and LIGA-like technologies. Ferromagnetic materials are used to fabricate
microscale stator and rotor, and windings can be deposited on the stator, see Figure 15.7.
The quadrature and direct magnetic axes are fixed with the microrotor, which rotates with angular
velocity
ω
r
. These magnetic axes rotate with the angular velocity
ω
. Assume that the initial conditions
are zero. Hence, the angular displacements of the rotor
θ
r
and the angular displacement of the quadrature
magnetic axis
θ
are equal, and
The magnetizing reluctance ℜ
m
is a function of the rotor angular displacement
θ
r
. Using the number
of turns N
S
, the magnetizing inductance is
.
This magnetizing inductance varies twice per one revolution of the rotor and has minimum and maxi-
mum values, and
FIGURE 15.7 Microscale single-phase reluctance motor with rotational motion microstructure (microrotor).
di
dt
-----
rA
g
l
f
2A
f
µ
f
+ x 2d+()[]
N
2
µ
f
µ
0
A
f
A
g
--------------------------------------------------------
i–
2
µ
f
A
f
A
g
l
f
2A
f
µ
f
+ x 2d+()
-------------------------------------------------
iv
A
g
l
f
2A
f
µ
f
+ x 2d+()
N
2
µ
f
µ
0
A
f
A
g
-------------------------------------------------
u
a
++=
dx
dt
------
v=
dv
dt
-----
N
2
µ
f
2
µ
0
A
f
2
A
g
mA
g
l
f
2A
f
µ
f
+ x 2d+()[]
2
--------------------------------------------------------------
i
2
1
m
----
k
s1
xk
s2
x
2
+()
B
v
m
-----
v––=
θ
r
θω
r
τ
()
τ
d
t
0
t
ωτ
()
τ
d
t
0
t
== = .
L
m
θ
r
()
N
S
2
ℜ
m
θ
r
()
-----------------
=
L
m min
N
S
2
ℜ
m max
θ
r
()
-------------------------
=
θ
r
=0,
π
,2
π
,…
, L
m max
N
S
2
ℜ
m min
θ
r
()
-------------------------
=
θ
r
=
1
2
--
π
,
3
2
--
π
,
5
2
--
π
,…
r
T
e
,
Quadrature magnetic axis
Stator
Rotor
ω
ψ
0
)(
r0
t
t
r
r
d
u
as
(t)
r
s
, L
s
s
N
Direct magnetic axis
i
as
as
r
ICs
ω
ω
θθ
θθ
∫
9258_C015.fm Page 16 Tuesday, October 2, 2007 3:35 AM

Rotational and Translational Microelectromechanical Systems 15-17
Assume that this variation is a sinusoidal function of the rotor angular displacement. Then,
where is the average value of the magnetizing inductance and L
∆m
is half of the amplitude of the
sinusoidal variation of the magnetizing inductance.
The plot for L
m
(
θ
r
) is documented in Figure 15.8.
The electromagnetic torque, developed by single-phase reluctance motors is found using the expression
for the coenergy W
c
(i
as
,
θ
r
). From W
c
(i
as
,
θ
r
) = one finds
The electromagnetic torque is not developed by synchronous reluctance motors if IC feeds the dc
current or voltage to the motor winding because Hence, conventional control algo-
rithms cannot be applied, and new methods, which are based upon electromagnetic features must be
researched. The average value of T
e
is not equal to zero if the current is a function of
θ
r
. As an illustration,
let us assume that the following current is fed to the motor winding:
Then, the electromagnetic torque is
and
The mathematical model of the microscale single-phase reluctance motor is found by using Kirchhoff’s
and Newton’s second laws
FIGURE 15.8 Magnetizing inductance L
m
(
θ
r
).
2
r
L
m min
L
m max
L
m
L
m
m
L
0
m
L
θππ
2
1
π
2
3
π
∆
∆
L
m
θ
r
() L
m
L
∆m
–= 2
θ
r
cos
L
m
1
2
--
(L
ls
L
m
L
∆m
2
θ
r
cos–+ )i
as
2
,
T
e
∂
W
c
i
as
,
θ
r
()
∂θ
r
---------------------------
∂
1
2
--
i
as
2
L
ls
L
m
L
∆m
–+ cos2
θ
r
()[]
∂θ
r
----------------------------------------------------------------------
L
∆m
i
as
2
2
θ
r
sin== =
T
e
L
∆m
i
as
2
= sin2
θ
r
.
i
as
i
M
Re= 2
θ
r
sin()
T
e
L
∆m
i
as
2
2
θ
r
sin L
∆m
i
M
2
= Re 2
θ
r
sin()
2
= sin2
θ
r
0≠
T
eav
1
π
---
L
∆m
i
as
2
0
π
= sin2
θ
r
d
θ
r
1
4
--
L
∆m
i
M
2
=
u
as
r
s
i
as
d
ψ
as
dt
----------
(circuitry equation)+=
T
e
B
m
ω
r
– T
L
– J
d
2
θ
r
dt
2
----------
= torsional-mechanical equation()
9258_C015.fm Page 17 Tuesday, October 2, 2007 3:35 AM

15-18 Mechatronic Systems, Sensors, and Actuators
From one obtains a set of three first-order nonlinear differential
equations. In particular, we have
Example 15.5.3: Mathematical Model of Two-Phase Permanent-Magnet
Stepper Micromotors
For two-phase permanent-magnet stepper micromotors, we have
where the flux linkages are
ψ
as
= L
asas
i
as
+ L
asbs
i
bs
+
ψ
asm
and
ψ
bs
= L
bsas
i
as
+ L
bsbs
i
bs
+
ψ
bsm
.
Here, u
as
and u
bs
are the phase voltages in the stator microwindings as and bs; i
as
and i
bs
are the phase
currents in the stator microwindings;
ψ
as
and
ψ
bs
are the stator flux linkages; r
s
are the resistances of the
stator microwindings; L
asas
, L
asbs
, L
bsas
, and L
bsbs
are the mutual inductances.
The electrical angular velocity and displacement are found using the number of rotor tooth RT,
where
ω
r
and
ω
rm
are the electrical and rotor angular velocities, and
θ
r
and
θ
rm
are the electrical and rotor
angular displacements.
The flux linkages are functions of the number of the rotor tooth RT, and the magnitude of the flux
linkages produced by the permanent magnets
ψ
m
. In particular,
The self-inductance of the stator windings is
The stator microwindings are displaced by 90 electrical degrees. Hence, the mutual inductances between
the stator microwindings are zero, L
asbs
= L
bsas
= 0.
Then, we have
ψ
as
(L
ls
L
m
L
∆m
cos2
θ
r
–+ )i
as
= ,
di
as
dt
--------
r
s
L
ls
L
m
L
∆m
–+ cos2
θ
r
-------------------------------------------------
i
as
2L
∆m
L
ls
L
m
L
∆m
–+ cos2
θ
r
-------------------------------------------------
i
as
ω
r
sin2
θ
r
1
L
ls
L
m
L
∆m
–+ cos2
θ
r
-------------------------------------------------
u
as
+–=
d
ω
r
dt
---------
1
J
--
L
∆m
i
as
2
2
θ
r
sin B
m
ω
r
– T
L
–()=
d
θ
r
dt
--------
ω
r
=
u
as
r
s
i
as
d
ψ
as
dt
----------
+=
u
bs
r
s
i
bs
d
ψ
bs
dt
----------
+=
ω
r
RT
ω
rm
=
θ
r
RT
θ
rm
=
ψ
asm
ψ
m
cos RT
θ
rm
()and=
ψ
bsm
ψ
m
sin RT
θ
rm
()=
L
ss
L
asas
L
bsbs
L
ls
L
m
+===
ψ
as
L
ss
i
as
ψ
m
cos RT
θ
rm
()and+=
ψ
bs
L
ss
i
bs
ψ
m
sin RT
θ
rm
()+=
9258_C015.fm Page 18 Tuesday, October 2, 2007 3:35 AM
Rotational and Translational Microelectromechanical Systems 15-19
Taking note of the circuitry equations, one has
Therefore, we obtain
Using Newton’s second law, we have
The expression for the electromagnetic torque developed by permanent-magnet stepper micromotors
must be found. Taking note of the relationship for the coenergy
one finds the electromagnetic torque:
Hence, the transient evolution of the phase currents i
as
and i
bs
, rotor angular velocity
ω
rm
, and dis-
placement
θ
rm
, is modeled by the following differential equations:
u
as
r
s
i
as
dL
ss
i
as
ψ
m
cos RT
θ
rm
()+[]
dt
--------------------------------------------------------------
+ r
s
i
as
L
ss
di
as
dt
--------
RT
ψ
m
ω
rm
– sin RT
θ
rm
()+==
u
bs
r
s
i
bs
dL
ss
i
bs
ψ
m
sin RT
θ
rm
()+[]
dt
-------------------------------------------------------------
+ r
s
i
bs
L
ss
di
bs
dt
--------
RT
ψ
m
ω
rm
+ cos RT
θ
rm
()+==
di
as
dt
--------
r
s
L
ss
-----– i
as
RT
ψ
m
L
ss
---------------
ω
rm
sin RT
θ
rm
()
1
L
ss
-----
+ u
as
+=
di
bs
dt
--------
r
s
L
ss
-----– i
bs
RT
ψ
m
L
ss
---------------
–
ω
rm
cos RT
θ
rm
()
1
L
ss
-----
+ u
bs
=
d
ω
rm
dt
------------
1
J
--
T
e
B
m
ω
rm
T
L
––()=
d
θ
rm
dt
-----------
ω
rm
=
W
c
1
2
--
L
ss
i
as
2
L
ss
i
bs
2
+()
ψ
m
i
as
RT
θ
rm
()cos
ψ
m
i
bs
RT
θ
rm
()W
PM
+sin++=
T
e
∂
W
c
∂θ
rm
-----------
RT
ψ
m
i
as
RT
θ
rm
()i
bs
RT
θ
rm
()cos–sin[]–==
di
as
dt
--------
r
s
L
ss
-----
i
as
RT
ψ
m
L
ss
---------------
ω
rm
RT
θ
rm
()
1
L
ss
-----
u
as
+sin+–=
di
bs
dt
--------
r
s
L
ss
-----
i
bs
–
RT
ψ
m
L
ss
---------------
ω
rm
RT
θ
rm
()
1
L
ss
-----
u
bs
+cos–=
d
ω
rm
dt
------------
RT
ψ
m
J
---------------
i
as
RT
θ
rm
()sin i
bs
RT
θ
rm
()cos–[]
B
m
J
------
ω
rm
–
1
J
--
T
L
––=
d
θ
rm
dt
-----------
ω
rm
=
9258_C015.fm Page 19 Tuesday, October 2, 2007 3:35 AM
15-20 Mechatronic Systems, Sensors, and Actuators
These four nonlinear differential equations are rewritten in the state-space form as
The analysis of the torque equation
guides one to the conclusion that the expressions for a balanced two-phase current sinusoidal set is
If these phase currents are fed, the electromagnetic torque is a function of the current magnitude i
M
, and
The phase currents needed to be fed are the functions of the rotor angular displacement. Assuming
that the inductances are negligibly small, we have the following phase voltages needed to be supplied:
Example 15.5.4: Mathematical Model of Two-Phase Permanent-Magnet
Synchronous Micromotors
Consider two-phase permanent-magnet synchronous micromotors. Using Kirchhoff’s voltage law, we have
where the flux linkages are expressed as
ψ
as
= L
asas
i
as
+ L
asbs
i
bs
+
ψ
asm
and
ψ
bs
= L
bsas
i
as
+ L
bsbs
i
bs
+
ψ
bsm
.
The flux linkages are periodic functions of the angular displacement (rotor position), and let
di
as
dt
--------
di
bs
dt
--------
d
ω
rm
dt
--------------
d
θ
rm
dt
-------------
r
s
L
ss
-----
– 000
0
r
s
L
ss
-----
– 00
00
B
m
J
------
– 0
0010
i
as
i
bs
ω
rm
θ
rm
=
RT
ψ
m
L
ss
---------------
ω
rm
RT
θ
rm
()sin
RT
ψ
m
L
ss
---------------
ω
rm
RT
θ
rm
()cos–
RT
ψ
m
J
---------------
i
as
RT
θ
rm
()sin i
bs
RT
θ
rm
()cos–[]–
0
+
1
L
ss
-----
0
0
1
L
ss
-----
00
00
u
as
u
bs
0
0
1
J
--
0
– T
L
+
T
e
RT
ψ
m
i
as
RT
θ
rm
()sin i
bs
RT
θ
rm
()cos–[]–=
i
as
2i
M
RT
θ
rm
()and i
bs
2i
M
RT
θ
rm
()cos=sin–=
T
e
2RT
ψ
m
i
M
=
u
as
2u
M
RT
θ
rm
()and u
bs
2u
M
RT
θ
rm
()cos=sin–=
u
as
r
s
i
as
d
ψ
as
dt
----------
+=
u
bs
r
s
i
bs
d
ψ
bs
dt
----------
+=
ψ
asm
ψ
m
θ
rm
and
ψ
bsm
sin
ψ
m
θ
rm
cos–==
9258_C015.fm Page 20 Tuesday, October 2, 2007 3:35 AM

Rotational and Translational Microelectromechanical Systems 15-21
The self-inductances of the stator windings are found to be
The stator windings are displaced by 90 electrical degrees, and hence, the mutual inductances between
the stator windings are L
asbs
= L
bsas
=
0. Thus, we have
Therefore, one finds
Using Newton’s second law
we have
The expression for the electromagnetic torque developed by permanent-magnet motors can be obtained
by using the coenergy
Then, one has
Augmenting the circuitry transients with the torsional-mechanical dynamics, one finds the mathemat-
ical model of two-phase permanent-magnet micromotors in the following form:
L
ss
L
asas
L
bsbs
L
ls
L
m
+===
ψ
as
L
ss
i
as
ψ
m
θ
rm
andsin+
ψ
bs
L
ss
i
bs
ψ
m
θ
rm
cos–==
u
as
r
s
i
as
dL
ss
i
as
ψ
m
θ
rm
sin+()
dt
-------------------------------------------------
+ r
s
i
as
L
ss
di
as
dt
--------
ψ
m
ω
rm
θ
rm
cos++==
u
bs
r
s
i
bs
dL
ss
i
bs
ψ
m
θ
rm
cos–()
dt
-------------------------------------------------
+ r
s
i
bs
L
ss
di
bs
dt
--------
ψ
m
ω
rm
θ
rm
sin–+==
T
e
B
m
ω
rm
– T
L
– J
d
2
θ
rm
dt
2
-------------
=
d
ω
rm
dt
------------
1
J
--
T
e
B
m
ω
rm
– T
L
–()=
d
θ
rm
dt
-----------
ω
rm
=
W
c
1
2
--
L
ss
i
as
2
L
ss
i
bs
2
+()
ψ
m
i
as
θ
rm
sin
ψ
m
i
bs
θ
rm
cos– W
PM
++=
T
e
∂
W
c
∂θ
rm
-----------
P
ψ
m
2
----------
i
as
θ
rm
cos i+
bs
θ
rm
sin()==
di
as
dt
--------
r
s
L
ss
-----
i
as
–
ψ
m
L
ss
-------
ω
rm
θ
rm
1
L
ss
-----
u
as
+cos–=
di
bs
dt
--------
r
s
L
ss
-----
i
bs
ψ
m
L
ss
-------
ω
rm
θ
rm
1
L
ss
-----
u
bs
+sin+–=
d
ω
rm
dt
------------
P
ψ
m
2J
----------
i
as
θ
rm
i
bs
θ
rm
sin+cos()
B
m
J
------
ω
rm
–
1
J
--
T
L
–=
d
θ
rm
dt
-----------
ω
rm
=
9258_C015.fm Page 21 Tuesday, October 2, 2007 3:35 AM

15-22 Mechatronic Systems, Sensors, and Actuators
For two-phase motors (assuming the sinusoidal winding distributions and the sinusoidal mmf wave-
forms), the electromagnetic torque is expressed as
Hence, to guarantee the balanced operation, one feeds
to maximize the electromagnetic torque. In fact, one obtains
The air-gap mmf and the phase current waveforms are plotted in Figure 15.9.
15.6 Control of MEMS
Mathematical models of MEMS can be developed with different degrees of complexity. It must be
emphasized that in addition to the models of microscale motion devices, the fast dynamics of ICs should
be examined. Due to the complexity of complete mathematical models of ICs, impracticality of the
developed equations, and very fast dynamics, the IC dynamics can be modeled using reduced-order
differential equation or as unmodeled dynamics. For MEMS, modeled using linear and nonlinear dif-
ferential equations
different control algorithms can be designed.
Here, the state, control, output, and reference (command) vectors are denoted as x, u, y, and r;
parameter uncertainties (e.g., time-varying coefficients, unmodeled dynamics, unpredicted changes, etc.)
are modeled using z and p vectors.
FIGURE 15.9 Air-gap mmf and the phase current waveforms.
0 1 2 3 4 5 6 7 8 9 10
–1
–
0.8
–
0.6
–
0.4
–
0.2
0
0.2
0.4
0.6
0.8
1
T
e
P
ψ
m
2
----------
i
as
cos
θ
rm
i
bs
sin
θ
rm
+()=
i
as
2i
M
θ
rm
and i
bs
2i
M
θ
rm
sin=cos=
T
e
P
ψ
m
2
----------
i
as
θ
rm
cos i
bs
θ
rm
sin+()
P
ψ
m
2
----------
2i
M
cos
2
θ
rm
sin
2
θ
rm
+()
P
ψ
m
2
----------
i
M
== =
x
·
t() Ax Bu,+= u
min
uu
max
,≤≤ yHx=
x
·
t() F
z
t, x, r, z()B
p
t, x, p()u,+= u
min
uu
max
,≤≤ yHx()=
9258_C015.fm Page 22 Tuesday, October 2, 2007 3:35 AM

Rotational and Translational Microelectromechanical Systems 15-23
The matrices of coefficients are A, B, and H. The smooth mapping fields of the nonlinear model are
denoted as F
z
(⋅), B
p
(⋅), and H(⋅).
It should be emphasized that the control is bounded. For example, using the IC duty ratio d
D
as the
control signal, we have 0 ≤ d
D
≤ 1 or −1 ≤ d
D
≤ +1. Four-quadrant ICs are used due to superior
performance, and −1 ≤ d
D
≤ +1. Hence, we have −1 ≤ u ≤ +1. However, in general, u
min
≤ u ≤ u
max
.
15.6.1 Proportional-Integral-Derivative Control
Many MEMS can be controlled by the proportional-integral-derivative (PID) controllers, which, taking
note of control bounds, are given as [9]
where k
pj
, k
ij
,
and k
dj
are the matrices of the proportional, integral, and derivative feedback gains;
ς
,
β
,
σ
,
µ
,
α
, and
γ
are the nonnegative integers.
In the nonlinear PID controllers, the tracking error is used. In particular,
Linear bounded controllers can be straightforwardly designed. For example, letting
ς
=
β
=
σ
=
µ
= 0,
we have the following linear PI control law:
The PID controllers with the state feedback extension can be synthesized as
where V(e, x) is the function that satisfies the general requirements imposed on the Lyapunov pair [9],
e.g., the sufficient conditions for stability are used.
It is evident that nonlinear feedback mappings result, and the nonquadratic function V(e, x) can be
synthesized and used to obtain the control algorithm and feedback gains.
15.6.2 Tracking Control
Tracking control is designed for the augmented systems, which are modeled using the state variables and
the reference dynamics. In particular, from
ut() sat
u
min
u
max
e, etd ,
de
dt
-----
=
sat
u
min
u
max
k
pj
e
2j+1
2
β
+1
---- ---- -----
j=0
ς
k
ij
e
2j+1
2
µ
+1
----- ---- ----
j=0
σ
integral
dt
k
dj
e
·
2j+1
2
γ
+1
------ --- ---
j=0
α
derivative
++
proportional
, u
min
uu
max
≤≤=
et()
rt()
reference/command
yt()
output
–=
ut() sat
u
min
u
max
k
p0
et() k
i0
et td+=
ut() sat
u
min
u
max
e, x()=
sat
u
min
u
max
k
pj
e
2j+1
2
β
+1
---- ---- -----
j=0
ς
k
ij
e
2j+1
2
µ
+1
------- --- ---
j=0
σ
dt
k
dj
e
·
2j+1
2
γ
+1
----- --- ----
j=0
α
derivative
+
integral
Gt()B
∂
Ve, x()
∂
e
x
---------------------
++
proportional
, u
min
uu
max
≤≤=
x
·
t() Ax Bu,+= x
·
ref
t() rt() yt()–= rt() Hx t()–=
9258_C015.fm Page 23 Tuesday, October 2, 2007 3:35 AM
