Bichop R.H. (Ed.) Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling

Подождите немного. Документ загружается.

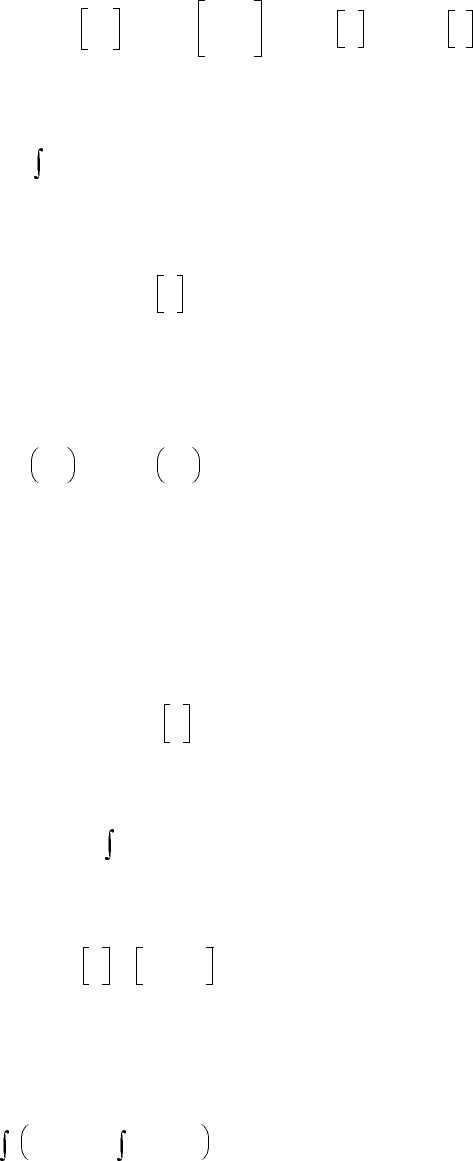
15-24 Mechatronic Systems, Sensors, and Actuators

one finds

Minimizing the quadratic performance functional

one finds the control law using the first-order necessary condition for optimality. In particular, we have

Here, Q is the positive semi-definite constant-coefficient matrix, and G is the positive weighting constant-

coefficient matrix.

The solution of the Hamilton–Jacobi equation

is satisfied by the quadratic return function V = Here, K is the symmetric matrix, which must

be found by solving the nonlinear differential equation

The controller is given as

From one has

Therefore, we obtain the integral control law

In this control algorithm, the error vector is used in addition to the state feedback.

As was illustrated, the bounds are imposed on the control, and u

min

≤ u ≤ u

max

. Therefore, the bounded

controllers must be designed. Using the nonquadratic performance functional [9]

t() A

r,++= yHx,= x

ref

,= A

A 0

H– 0

,= B

,= N

Gu+()td

1–

–

∂

--------

1–

–==

∂

--------

∂

-------–

∂

--------

∂

--------

1–

∂

--------

–+=

– QA

1–

K,–++= Kt

() K

1–

– G

1–

–

ref

t() et()=

ref

t() et()td=

ut() G

1–

– K

xt()

eet()dt

G tan

1–

u+ ud td

9258_C015.fm Page 24 Tuesday, October 2, 2007 3:35 AM

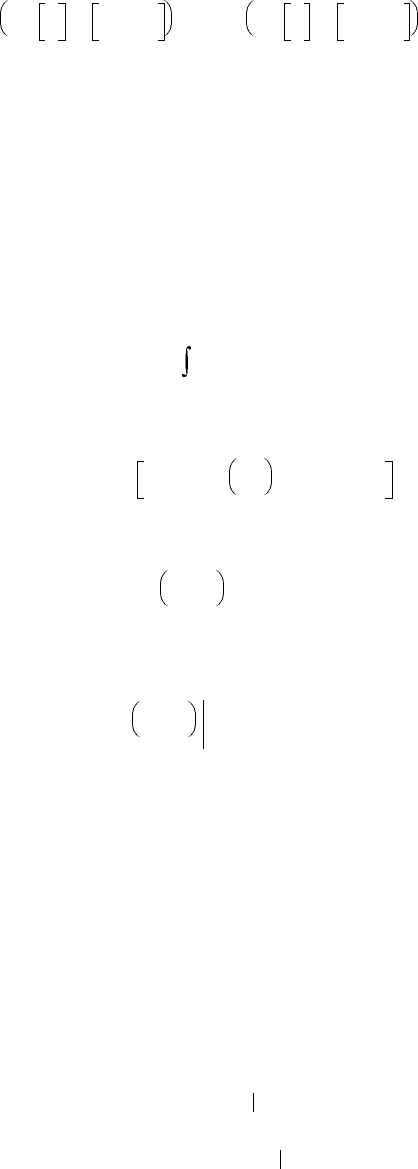
Rotational and Translational Microelectromechanical Systems 15-25

with positive semi-definite constant-coefficient matrix Q and positive-definite matrix G, one finds

This controller is obtained assuming that the solution of the functional partial differential equation

can be approximated by the quadratic return function

where K is the symmetric matrix.

15.6.3 Time-Optimal Control

A time-optimal controller can be designed using the functional

Taking note of the Hamilton–Jacobi equation

the relay-type controller is found to be

This “optimal” control algorithm cannot be implemented in practice due to the chattering phenom-

enon. Therefore, relay-type control laws with dead zone

are commonly used.

15.6.4 Sliding Mode Control

Soft-switching sliding mode control laws are synthesized in [9]. Sliding mode soft-switching algorithms

provide superior performance, and the chattering effect is eliminated.

To design controllers, we model the states and errors dynamics as

The smooth sliding manifold is

ut() G

1–

xt()

eet()td

tanh– sat

1–

xt()

eet()td

,–≈= 1– u 1≤≤

()td

∂

-------

= –

min

1≤u≤1–

∂

--------

u+()+

u sgn–= B

∂

--------

,1u 1≤≤–

∂

--------

sgn–=

dead zone

,1u 1≤≤–

t() Ax Bu,+ 1 u 1≤≤–=

t() Nr

t() HAx HBu––=

Mt, x, e()R

Š0

∈ XE

t, x, e()×× 0={}=

t, x, e()R

Š0

∈ XE

t, x, e()×× 0={}

j=1

∩

9258_C015.fm Page 25 Tuesday, October 2, 2007 3:35 AM

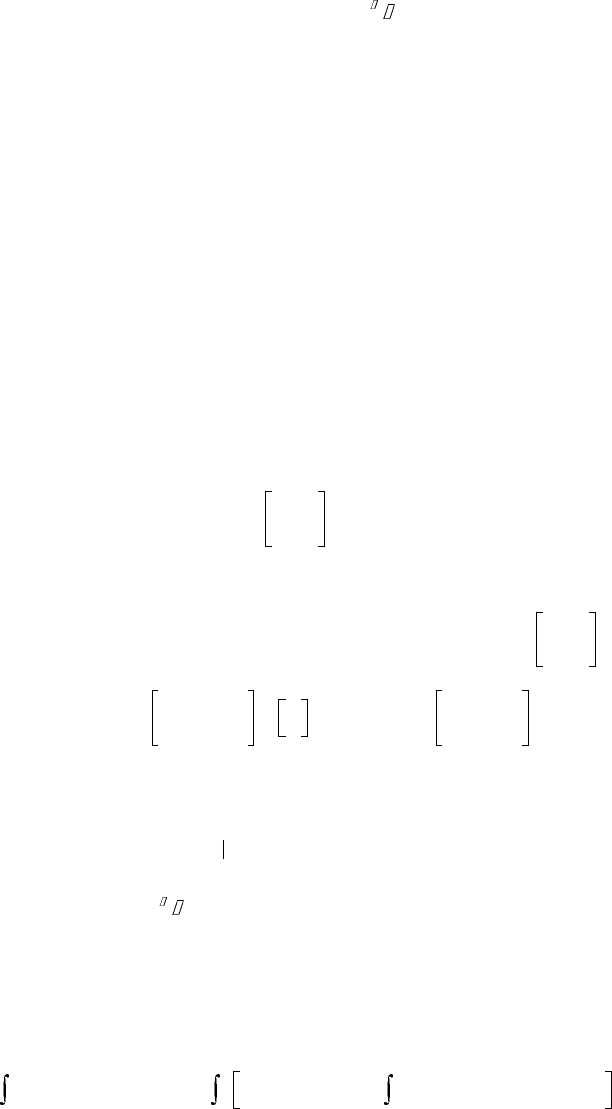
15-26 Mechatronic Systems, Sensors, and Actuators

The time-varying nonlinear switching surface is

(t, x, e) = K

(t, x, e) = 0. The soft-switching control

law is given as

where

(⋅) is the continuous real-analytic function of class C ( ≥ 1), for example, tanh and erf.

15.6.5 Constrained Control of Nonlinear MEMS: Hamilton–Jacobi Method

Constrained optimization of MEMS is a topic of great practical interest. Using the Hamilton–Jacobi theory,

the bounded controllers can be synthesized for continuous-time systems modeled as

Here, x

MEMS

∈ X

is the state vector; u ∈ U is the vector of control inputs: y ∈ Y is the measured output;

(⋅), B

(⋅) and H(⋅) are the smooth mappings; F

(0) = 0, B

(0) = 0, and H(0) = 0; and w is the nonnegative

integer.

To design the tracking controller, we augment the MEMS dynamics

with the exogenous dynamics

Using the augmented state vector

one obtains

The set of admissible control U consists of the Lebesgue measurable function u(⋅), and a bounded

controller should be designed within the constrained control set

We map the control bounds imposed by a bounded, integrable, one-to-one, globally Lipschitz, vector-

valued continuous function Φ ∈C

( ≥ 1). Our goal is to analytically design the bounded admissible state-

feedback controller in the closed form as u = Φ(x). The most common Φ are the algebraic and transcen-

dental (exponential, hyperbolic, logarithmic, trigonometric) continuously differentiable, integrable, one-

to-one functions. For example, the odd one-to-one integrable function tanh with domain (−∞, +∞) maps

the control bounds. This function has the corresponding inverse function tanh

−1

with range (−∞, +∞).

The performance cost to be minimized is given as

where G

−1

∈⺢

m ×m

is the positive-definite diagonal matrix.

ut, x, e()G

φυ

(),–= 1 u 1≤≤– , G 0>

MEMS

t() F

MEMS

()B

MEMS

()u

2w+1

,+= yHx

MEMS

min

max

≤≤ , x

MEMS

() x

MEMS

t() F

MEMS

()B

MEMS

()u

2w+1

+= yHx

MEMS

()=

min

max

≤≤ , x

MEMS

() x

MEMS

ref

t() Nr y– Nr H x

MEMS

().–==

MEMS

ref

= X∈

t() Fx, r()Bx()u

2w+1

,+ u

min

max

,≤≤ xt

() x

,= x

MEMS

ref

Fx, r()

MEMS

()

H– x

MEMS

()

+ r, Bx()

MEMS

()

UuR

imin

imax

,≤≤∈{= i 1,…,m }= .

x() W

u()+[]td

∞

x() 2w 1+()Φ

1–

u()()

1–

diag u

()ud+ td

∞

9258_C015.fm Page 26 Tuesday, October 2, 2007 3:35 AM

Rotational and Translational Microelectromechanical Systems 15-27

Performance integrands W

(⋅) and W

(⋅) are real-valued, positive-definite, and continuously differen-

tiable integrand functions. Using the properties of Φ one concludes that inverse function Φ

−1

is integrable.

Hence, integral

exists.

Example

Consider a nonlinear dynamic system

Taking note of

one has the positive-definite integrand

In general, if the hyperbolic tangent is used to map the saturation effect, for the single-input case, one has

Necessary conditions that the control function u(·) guarantees a minimum to the Hamiltonian

are: first-order necessary condition n1,

and second-order necessary condition n2,

The positive-definite return function V(·), V ∈ C

≥ 1, is

The Hamilton–Jacobi–Bellman equation is given as

1–

u()()

1–

diag u

()ud

------

ax bu

,+= u

min

max

≤≤

u() 2w 1+()Φ

1–

u()()

1–

diag u

()ud=

u() 3tanh

1–

tanh

1–

1 u

–()ln++ , G

1–

== =

u() 2w 1+()u

tanh

1–

---

2w+1

tanh

1–

---

2w+1

–

---------------

–==

x() 2w 1+()+Φ

1–

u()()

1–

diag u

()ud

∂

Vx()

∂

-----------------

Fx, r()Bx()u

2w+1

+[]+=

∂

-------

∂

---------------------

() inf

u∈U

, u()inf Jx

, Φ ·()()0≥==

∂

∂t

-------–

min

u∈U

x() 2w 1+()+Φ

1–

u()()

1–

diag u

()ud

∂

Vx()

∂

-----------------

Fx, r()Bx()u

2w+1

+[]+=

9258_C015.fm Page 27 Tuesday, October 2, 2007 3:35 AM

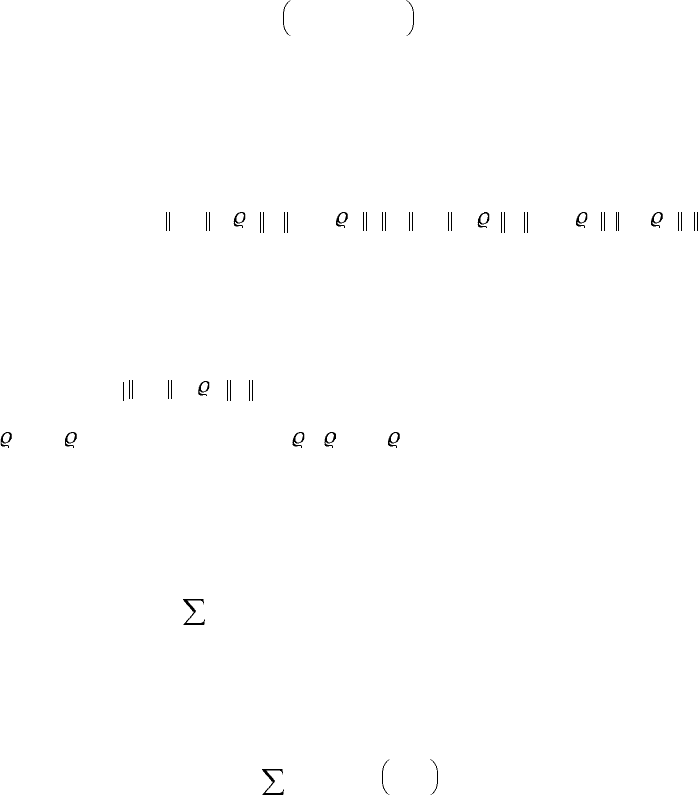
15-28 Mechatronic Systems, Sensors, and Actuators

The controller should be derived by finding the control value that attains the minimum to nonqua-

dratic functional. The first-order necessary condition (n1) leads us to an admissible bounded control

law. In particular,

The second-order necessary condition for optimality (n2) is met because the matrix G

−1

is positive-

definite. Hence, a unique, bounded, real-analytic, and continuous control candidate is designed.

If there exists a proper function V(x) which satisfies the Hamilton–Jacobi equation, the resulting

closed-loop system is robustly stable in the specified state X and control U sets, and robust tracking is

ensured in the convex and compact set XY(X

,U,R,E

). That is, there exists an invariant domain of stability

and control u(·), u ∈U steers the tracking error to the set

Here

and

are the KL-functions; and

, and

are the K-functions.

The solution of the functional equation should be found using nonquadratic return functions. To

obtain V(·), the performance cost must be evaluated at the allowed values of the states and control. Linear

and nonlinear functionals admit the final values, and the minimum value of the nonquadratic cost is

given by power-series forms [9]. That is,

The solution of the partial differential equation is satisfied by a continuously differentiable positive-

definite return function

where matrices K

are found by solving the Hamilton–Jacobi equation.

The quadratic return function in V(x) = x

x is found by letting

= 0. This quadratic candidate

may be employed only if the designer enables to neglect the high-order terms in Taylor’s series expansion.

Using

= 1 and

= 0, one obtains

while for

= 4 and

= 1, we have the following function:

u Φ GB x()

∂

Vx()

∂

---------------

– , u ∈U=

Sx ∈R

, e ∈R

: xt()

, t()≤

u(), et()

, t()

r()

y(),++≤+{=

x ∀∈XX

,U(), t ∀∈[t

, ∞), e ∀∈EE

, R, Y()}R

× ,⊂

() e ∈ R

: e

∈ E

, x ∈ XX

,U(), r ∈ R, y ∈ Y, t ∈ t

, ∞[){=

et()

,t()

0, e ∈ EE

,R,Y(), t∀ ∈ t

,∞)[∀≥+≤}R

⊂

min

()

2 i+

+1()

------ ---- ------ -------

i=0

0, 1, 2, …,

0, 1, 2,…===

Vx()

2 i

1++()

---------------------------

i=0

------- --- -----

----- --- -------

Vx()

()

Vx()

2/3

()

2/3

4/3

()

4/3

-----

5/3

()

5/3

()

++ + +=

9258_C015.fm Page 28 Tuesday, October 2, 2007 3:35 AM

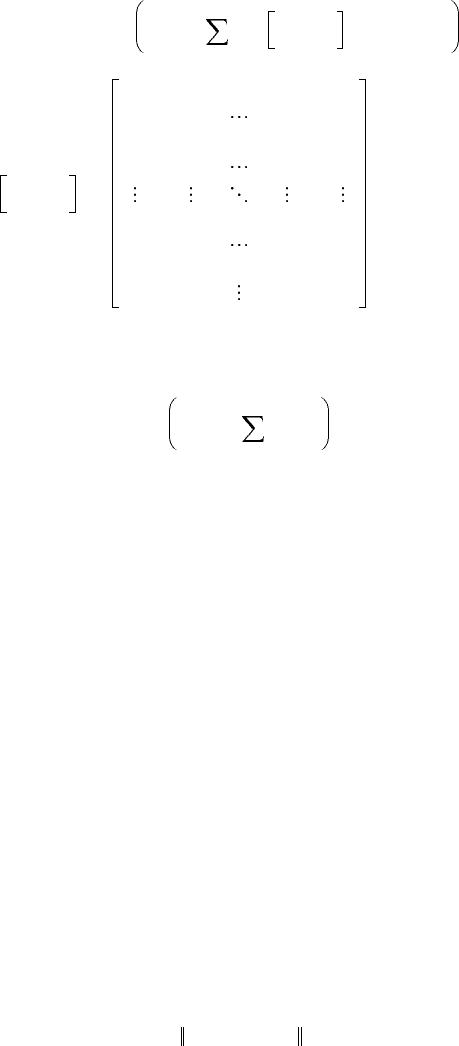
Rotational and Translational Microelectromechanical Systems 15-29

The nonlinear bounded controller is given as

If matrices K

are diagonal, we have the following control algorithm:

15.6.6 Constrained Control of Nonlinear Uncertain MEMS: Lyapunov

Method

Over the horizon [t

, ∞) we consider the dynamics of MEMS modeled as

where t ∈⺢

≥0

is the time; x ∈X is the state-space vector; u ∈U is the vector of bounded control inputs;

r ∈R and y ∈Y are the measured reference and output vectors; z ∈Z and p ∈P are the parameter

uncertainties, functions z(·) and p(·) are Lebesgue measurable and known within bounds; Z and P are

the known nonempty compact sets; and F

(·), B

(·), and H(·) are the smooth mapping fields.

Let us formulate and solve the motion control problem by synthesizing robust controllers that guar-

antee stability and robust tracking. Our goal is to design control laws that robustly stabilize nonlinear

systems with uncertain parameters and drive the tracking error e(t) = r(t) − y(t), e ∈E robustly to the

compact set. For MEMS modeled by nonlinear differential equations with parameter variations, the

robust tracking of the measured output vector y ∈Y must be accomplished with respect to the measured

uniformly bounded reference input vector r ∈R.

The nominal and uncertain dynamics are mapped by F(·), B(·), and Ξ(·). Hence, the system evolution

is described as

There exists a norm of Ξ(t, x, u, z, p), and ≤

(t, x), where

(·) is the continuous

Lebesgue measurable function. Our goal is to solve the motion control problem, and tracking controllers

must be synthesized using the tracking error vector and the state variables. Furthermore, to guarantee

robustness and to expand stability margins, to improve dynamic performance, and to meet other require-

ments, nonqudratic Lyapunov functions V(t, e, x) will be used in stability analysis and design of robust

tracking control laws.

u Φ GB x()

diag xt()

i−

----- --- ----

t()xt()

------ ---- -----

i=0

– ,=

diag xt()

i−

----- --- ----

i−

----- --- ----

0 00

0 x

i−

---- ---- ----

00 x

c−1

i−

----- ---- ---

0 x

i−

----- --- ----

u Φ GB x()

2i+1

---- --- -----

i=0

–=

x· t() F

t, x, r, z()B

t, x, p()u, y+ Hx(), u

min

max

, xt

()≤≤ x

===

x· t() Ft, x, r()Bt, x()u Ξ t, x, u, z, p(), y++ Hx(),==u

min

max

≤≤ , xt

() x

Ξ t, x, u,z, p()

9258_C015.fm Page 29 Tuesday, October 2, 2007 3:35 AM

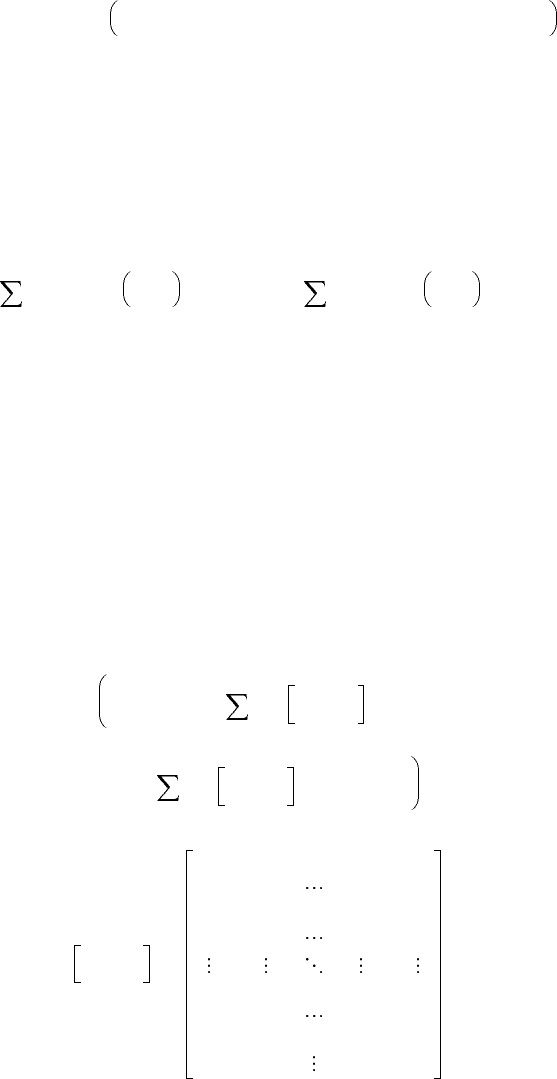
15-30 Mechatronic Systems, Sensors, and Actuators

Suppose that a set of admissible control U consists of the Lebesgue measurable function u(·). It was

demonstrated that the Hamilton–Jacobi theory can be used to find control laws, and the minimization

of nonquadratic performance functionals leads one to the bounded controllers.

Letting u = Φ(t, e, x), one obtains a set of admissible controllers. Applying the error and state feedback

we define a family of tracking controllers as

where Ω(·) is the nonlinear function; G

(·) and G

(·) are the diagonal matrix-functions defined on [t

,∞);

(·) is the matrix-function; and V(·) is the continuous, differentiable, and real-analytic function.

Let us design the Lyapunov function. This problem is a critical one and involves well-known difficulties.

The quadratic Lyapunov candidates can be used. However, for uncertain nonlinear systems, nonquadratic

functions V(t, e, x) allow one to realize the full potential of the Lyapunov-based theory and lead us to

the nonlinear feedback maps which are needed to achieve conflicting design objectives. We introduce

the following family of Lyapunov candidates:

where K

(·) and K

(·) are the symmetric matrices;

, and

are the nonnegative integers;

= 0, 1,

2,…;

= 0, 1, 2,…;

= 0, 1, 2,…; and

= 0, 1, 2,…

The well-known quadratic form of V(t, e, x) is found by letting

= 0, and we have

By using

= 1,

= 0,

= 1, and

= 0, one obtains a nonquadratic candidate:

One obtains the following tracking control law:

u Ω x()Φt, e, x()Ωx()ΦG

t()B

t, x()

∂

Vt, e, x()

∂

-------------------------

t()Bt, x()

∂

Vt, e, x()

∂

-------------------------

– , s

-----

== =

Vt, e, x()

2 i

1++()

----------------------------

---- --- ------- --

t()e

------ --- -------

i=0

2 i

1++()

---------------------------

------ ---- -----

t()x

----- --- -------

i=0

Vt, e, x()

t()e

t()x+=

Vt, e, x()

t()e

t()x

+++=

u Ω x()ΦG

t()B

t, x()

diag et()

i−

----- ---- -----

t()

et()

----- ---- -------

i=0

–=

t()Bt, x()

diag

i=0

xt()

i−

------- --- --

t()xt()

---- --- --------

diag et()

i−

----- --- -----

i−

------ --- ----

0 00

0 e

i−

------- --- ---

00 e

b−1

i−

------ --- ----

0 e

i−

------- --- ---

9258_C015.fm Page 30 Tuesday, October 2, 2007 3:35 AM

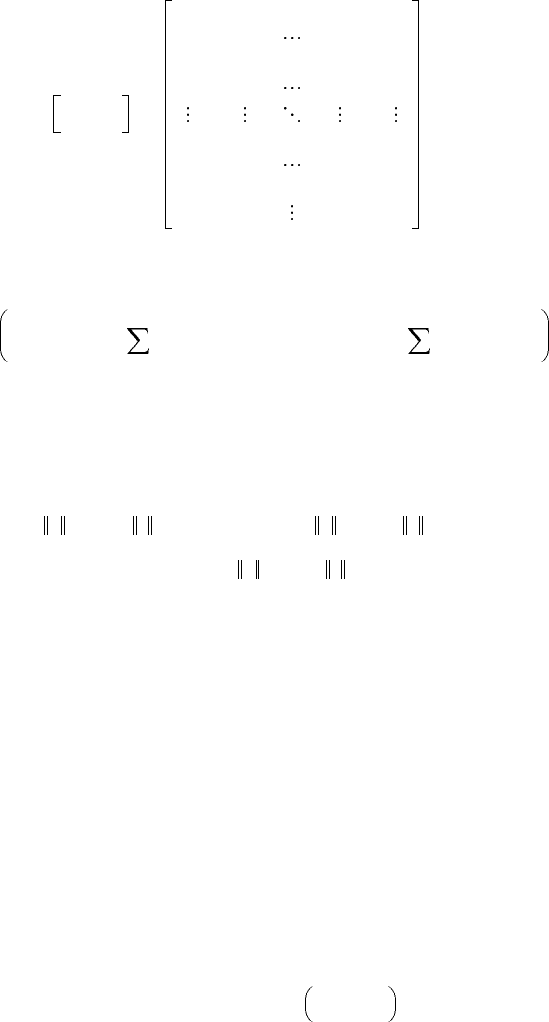
Rotational and Translational Microelectromechanical Systems 15-31

and

If matrices K

and K

are diagonal, we have

A closed-loop uncertain system is robustly stable in X(X

, U, Z, P) and robust tracking is guaranteed

in the convex and compact set E(E

, Y, R) if for reference inputs r ∈R and uncertainties in Z and P there

exists a C

(

≥ 1) function V(·), as well as K

∞

-functions

(·),

(·) and K-functions

(·),

(·), such that the following sufficient conditions:

are guaranteed in an invariant domain of stability S, and XE(X

, E

, U, R, Z, P) S.

The sufficient conditions under which the robust control problem is solvable were given. Computing

the derivative of the V(t, e, x), the unknown coefficients of V(t , e, x) can be found. That is, matrices

(·) and K

(·) are obtained. This problem is solved using the nonlinear inequality concept [9].

Example 15.6.1: Control of Two-Phase Permanent-Magnet

Stepper Micromotors

High-performance MEMS with permanent-magnet stepper micromotors have been designed and man-

ufactured. Controllers are needed to be designed to control permanent-magnet stepper micromotors,

and the angular velocity and position are regulated by changing the magnitude of the voltages applied

or currents fed to the stator windings (see Example 15.5.3). The rotor displacement is measured or

observed in order to properly apply the voltages to the phase windings. To solve the motion control

problem, the controller must be designed. It is illustrated that novel control algorithms are needed to be

deployed to maximize the torque developed. In fact, conventional controllers

cannot be used.

Using the coenergy concept, one finds the expression for the electromagnetic torque as given by

and thus, one must fed the phase currents as sinusoidal and cosinusoidal functions of the rotor displacement.

diag xt()

i−

------- --- --

i−

------ ---- --

0 00

0 x

i−

------ --- ---

00 x

n−1

i−

------ ---- --

0 x

i−

------ --- ---

u Ω x()ΦG

t()B

t, x()

t()

et()

2i+1

----- ---- ----

i=0

t()Bt, x()

t()xt()

2i+1

---- --- -----

i=0

+–=

x()

e()+ Vt, e, x()

x()

e()+≤≤

dV t, e, x()

-------------------------

– x()

e()–≤

⊆

1–

∂

-------

–= and u Φ G

1–

∂

--------

–=

– i

()sin i

()cos–[]=

9258_C015.fm Page 31 Tuesday, October 2, 2007 3:35 AM

15-32 Mechatronic Systems, Sensors, and Actuators

The mathematical model of permanent-magnet stepper micromotor was found in Example 15.5.3 as

The rotor resistance is a function of temperature because the resistivity is

[(1 +

(T° − 20°)].

Hence, r

(·) ∈[r

s min

s max

]. The susceptibility of the permanent magnets (thin films) decreases with

increasing temperature. Other servo-system parameters also vary; in particular, L

(·) ∈[L

ss min

ss max

] and

(·) ∈[B

m min

m max

The following equation of motion in vector form results:

Here, x ∈X and u ∈U are the state and control vectors, r ∈R and y ∈Y are the measured reference and

output, d ∈D is the disturbance, d = T

, and z ∈Z and p ∈P are the unknown and bounded parameter

uncertainties.

Our goal is to design the bounded control u(·) within the constrained set

= {u ∈ ⺢

: u

min

≤ u ≤ u

max

, u

min

< 0, u

max

> 0} ⺢

2Ž

An admissible control law, which guarantees a balanced two-phase voltage applied to the ab windings

and ensures the maximal electromagnetic torque production, is synthesized as

where e ∈E is the measured tracking error, e(t) = r(t) − y(t); Φ(·) is the bounded function (erf, sat, tanh),

and Φ ∈U, |Φ(·)| ≤ V

max

, V

max

is the rated voltage; G

(·), G

(·), and G

(·) are bounded and symmetric,

> 0, G

> 0; and V(·) is the C

(

≥ 1) continuously differentiable, real-analytic function.

For , u ∈U, r ∈R, d ∈D, z ∈Z, and p ∈P, we obtain the state evolution set X. The state-output

set is

-------

------

--------------

()sin

-- ---

++–=

-------

------

--------------

()cos–

-----

+–=

-----------

--------------

()sin i

()cos–[]

------

–

––=

----------

x· t() F

t, x, r, d, z()B

p()u,+= u

min

max

≤≤

() x

, x

, u

, y

== = =

⊂

()sin– 0

0 RT

()cos

Φ G

t()B

∂

Vt, x, e()

∂

-------------------------

t()B

∂

Vt, x, e()

∂

-------------------------

t()B

∂

Vt, x, e()

∂

-------------------------

X⊆

XY X

,U, R, D, Z, P()x, y()XY: x

, uU,∈∈×∈{ rR, dD, zZ, pP, t [t

, ∞)∈∈∈∈∈}=

9258_C015.fm Page 32 Tuesday, October 2, 2007 3:35 AM

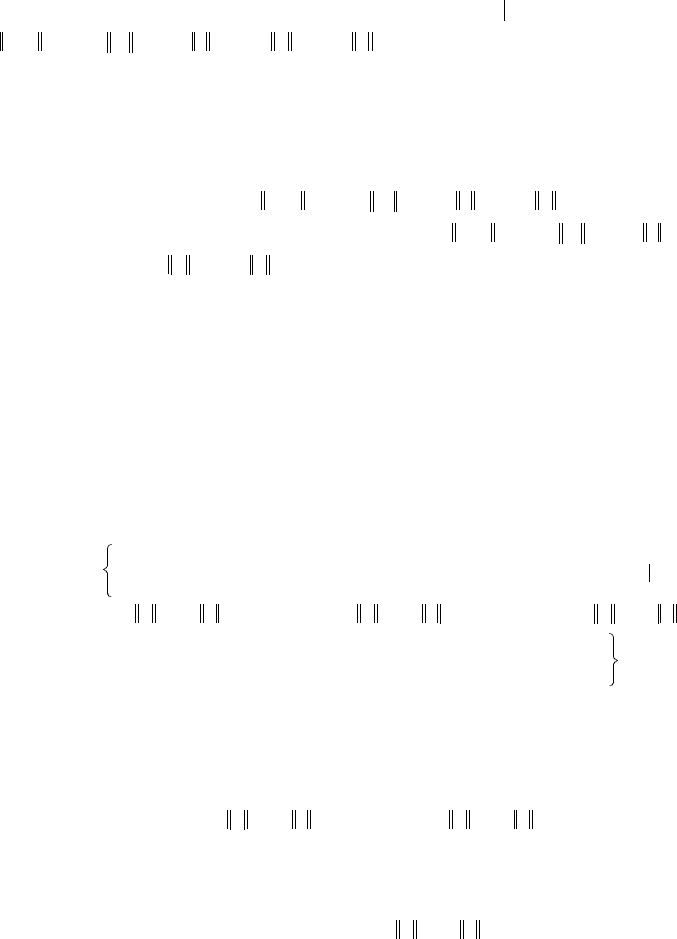
Rotational and Translational Microelectromechanical Systems 15-33

and a reference-output map can be found. Our goal is to find the bounded controller such that the tracking

error e(⋅):[t

,∞)→E with evolves in the specified closed set

Here,

(⋅) is the KL-function;

(⋅),

(⋅) and

(⋅) are the K-functions.

A positive-invariant domain of stability is found for the closed-loop system with x

∈X

, e

∈

, u ∈U,

r ∈R, d ∈D, z ∈Z and p ∈P. In particular,

where

(⋅) is the KL-function.

To study the robustness, tracking, and disturbance rejection, we consider a state-error set

The robust tracking, stability, and disturbance rejection are guaranteed if . The admissible set

is found by using the Lyapunov stability theory [9], and

where

(⋅),

(⋅) and

(⋅) are the K

∞

-functions; and

(⋅) and

(⋅) are the K-functions.

If in XE there exists a C

Lyapunov function V(t, x, e) such that for all

and on sufficient condition for stability (s1)

and inequality

which is the sufficient condition for stability s2, hold, then

1. Solution x(⋅):[t

,∞)→X for closed-loop system is robustly bounded and stable.

2. Convergence of the error vector e(⋅):[t

, ∞)→E to S

is ensured in XE.

3. XE is convex and compact, and

That is, if criteria (s1) and (s2) are guaranteed, we have

⊆

() e R

: e

, xXX

,U, R, D, Z, P(), t [t

, ∞)∈∈∈∈{=

et() ≤

t, e

()

r()

d()

y()

++ ++,

0, eEE

, R, D, Y(), t [t

, ∞)∈∀∈∀≥}

x{ R

, e R

: xt()

t, x

()

r()

d()++≤∈∈

, +=

x∀ XX

,U, R, D, Z, P(), t∀ [t

, ∞),∈∈ et()

t, e

()≤

r()+

d()

y()

, e∀ EE

, R, D, Y(), t∀ [t

, ∞) }∈∈++ ,

XE X

, E

,U, R, D, Z, P()x, e()XE: x

, e

, uU,∈∈∈×∈{=

rR, dD, zZ, pP, t [t

, ∞)∈∈∈∈∈ }

XE S

⊆

x R

,e R

: x

, e

, uU, rR, dD, zZ, pP∈∈∈∈∈∈∈∈∈

+ eVt, x, e()

e ,

dV t, x, e()

------------------------

x–

e ,–≤+≤≤

x∀ XX

,U, R, P, Z, P(), e∀ EE

, R, D, Y(), t [t

, ∞)∈∀∈∈

, e

, uU,∈∈∈

rR, dD, zZ,∈∈∈ pP∈ [t

, ∞)

eVt, x, e()

e+≤≤+

dV t, x, e()

------------------------

– x

e–≤

.⊆

XE S

.⊆

9258_C015.fm Page 33 Tuesday, October 2, 2007 3:35 AM