Bhushan B. Nanotribology and Nanomechanics: An Introduction
Подождите немного. Документ загружается.

636 Adrian B. Mann
it harder to initiate cracks and, hence, less useful as a way to evaluatefracture tough-
ness. To overcomethese problems the cube corner geometry, which generates larger
shear stresses than the Berkovichpyramid, has been used with nanoindentationtest-
ing to study fracture [92]. These studies have had mixed success, because the cube
corner geometry blunts very quickly when used on hard materials. In many cases,
brittle materials are very hard.
Depth sensing indentationis better suited to studying delamination of thin films.
Recent work extends the research conducted by Marshall et al. [93, 94], who ex-
amined the deformation of residually stressed films by indentation. A schematic of
their analysis is given by Fig. 12.24. Their indentations were several microns deep,
but the basic analysis is valid for nanoindentations. The analysis has been extended
to multilayers [95], which is important since it enables a quantitative assessment of
adhesion energy when an additional stressed film has been deposited on top of the
film and substrate of interest. The additional film limits the plastic deformation of
the film of interest and also applies extra stress that aids in the delamination. Af-
ter indentation, the area of the delaminated film is measured optically or with an
AFM to assess the extent of the delamination. This measurement, coupled with the
load-displacement data, enables quantitative assessment of the adhesion energy to
be made for metals [96] and polymers [97].
Δ
R
σ
R
σ
R
Δ
I
+ Δ
R
σ
I
+ σ
R
a)
b)
c)
d)
e)
σ
R
σ
R
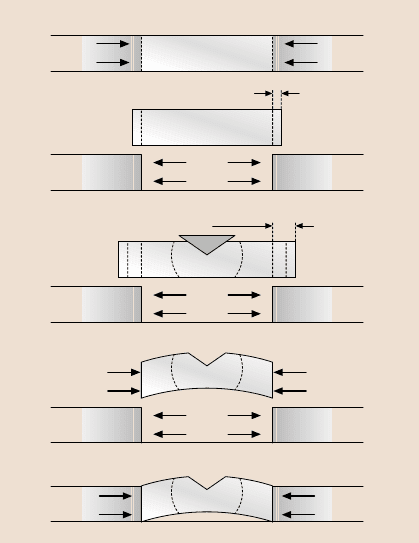
Fig. 12.24. To model de-
lamination Kriese et al. [95]
adapted the model developed
by Marshall and Evans [93].
The model considers a seg-
ment of removed stressed
film that is allowed to expand
and then indented, thereby
expanding it further. Replac-
ing the segment in its original
position requires an addi-
tional stress, and the segment
bulges upwards
12 Nanomechanical Properties of Solid Surfaces and Thin Films 637
12.4.5 Phase Transformations
The pressure applied to the surface of a material during indentation testing can be
very high. Equation (12.10) indicates that the pressure during plastic yielding is
about three times the yield stress. For many materials, high hydrostatic pressures
can cause phase transformations, and provided the transformation pressure is less
than the pressure required to cause plastic yielding, it is possible during indentation
testing to induce a phase transformation. This was first reported for silicon [98],
but it has also been speculated [99] that many other materials may show the same
effects. Most studies still focus on silicon because of its enormous technological
importance,although thereis some evidencethat germanium also undergoesa phase
transformation during the nanoindentationtesting [100].
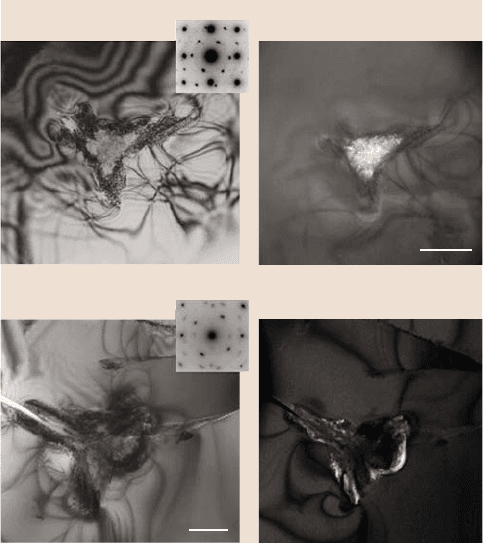
Recentresults [21,22,41,101,102]indicatethat there are actually multiple phase
transformations during the nanoindentation of silicon. TEM of nanoindentations in
diamond cubic silicon have shown the presence of amorphous-Si and the body-
centered cubic BC-8 phase (see Fig. 12.25). Micro-Raman spectroscopy has indi-
cated the presence of a further phase, the rhombhedral R-8 (see Fig. 12.26). For
a)
b)
600 nm
1 μm
Fig. 12.25. Bright-field and dark-field TEM of (a)smalland(b) large nanoindentations in Si.
In small nanoindents the metastable phase BC-8 is seen in thecenter, but for large nanoindents
BC-8 is confined to the edge of the indent, while the center is amorphous

638 Adrian B. Mann
140,000
120,000
100,000
80,000
60,000
40,000
20,000
0
Relative intensity
Wavenumber (cm
–1
)
Raman spectra for 10 u 1,600 nm nanoindents
~ 301 -
α-Si
~ 383 -
BC8-Si
~ 395 -
R8-Si
~ 432 -
BC8-Si
~ 520 -
DC-Si
~ 350 -
R8-Si
Fig. 12.26. Micro-Raman generally shows the BC-8 and R-8 Si phases that are at the edge
of the nanoindents, but the amorphous phase in the center is not easy to detect, as it is often
subsurface and the Raman peak is broad
many nanoindentations on silicon there is a characteristic discontinuity in the un-
loading curve (see Fig. 12.27), which seems to correlate with a phase transforma-
tion. The exact sequence in which the phases form is still highly controversial with
2
4
6
8
Contact resistance (log Ω)
40
30
20
10
0
Displacement (nm)
4003002001000
Load (mN)
Resistance
Discontinuity
resistance falls
by 97%
Load
Discontinuity
no acoustic
emission
Fig. 12.27. Nanoindentation curves for deep indents on Si show a discontinuity during un-
loading and simultaneously a large drop in contact resistance
12 Nanomechanical Properties of Solid Surfaces and Thin Films 639
some [42], suggesting that the sequence during loading and unloading is:
Increasing load →
Diamond cubic Si →β-Sn Si
← Decreasing load
BC-8 Si and R-8 Si ←β-Sn Si
Other groups [21, 22] suggest that the above sequence is only valid for shallow
nanoindentations that do not exhibit an unloading discontinuity. For large nanoin-
dentations that show an unloading discontinuity, they suggest the sequence will be:
Increasing load →
Diamond cubic Si →β-Sn Si
← Decreasing load
α-Si ← BC-8 Si and R-8 Si ← β-Sn Si
The disagreement is over the origin of the unloading discontinuity. Mann et al.
[21] suggestit is due to the formation of amorphoussilicon, while Gogotsi et al. [42]
believe it is the β-Sn Si to BC-8 or R-8 transformation. Mann et al. argue that the
high contact resistance before the discontinuity and the low contact resistance af-
terwards rule out the discontinuity being the metallic β-Sn Si transforming to the
more resistive BC-8 or R-8. The counterargumentis that amorphous Si is only seen
with micro-Raman spectroscopy when the unloading is very rapid or there is a large
nanoindentationwith no unloading discontinuity. The importance of unloading rate
and cracking in determining the phases present are further complications. The con-
troversywill remainuntil insitu characterizationof the phasespresent isundertaken.
12.5 Thin Films and Multilayers
In almost all real applications, surfaces are coated with thin films. These may be in-
tentionally added such as hard carbide coatings on a tool bit, or they may simply be
nativefilmssuch as anoxide layer. Itis also likelythat therewill beadsorbed filmsof
water and organic contaminants that can range from a single molecule in thickness
up to several nanometers. All of these films, whether native or intentionally placed
on the surface, will affect the surface’s mechanical behavior on the nanoscale. Ad-
sorbates can have a significant impact on the surface forces [3] and, hence, the geo-
metry and stability of asperity contacts. Oxide films can have dramatically different
mechanical properties to the bulk and will also modify the surface forces. Some of
the effects of native films have been detailed in the earlier sections on dislocation
nucleation and adhesive contacts.
The importanceof thin films in enhancingthe mechanicalbehaviorof surfaces is
illustrated by the abundance of publications on thin film mechanical properties (see
for instance Nix [88] or Cammarata [31] or Was and Foe cke [103]). In the following
sections, the mechanical properties of films intentionally deposited on the surface
will be discussed.
640 Adrian B. Mann
12.5.1 Thin Films
Measuring the mechanical properties of a single thin surface film has always been
difficult. Any measurement performed on the whole sample will inevitably be dom-
inated by the bulk substrate. Nanoindentation,since it looksat the mechanical prop-
erties of a very small region close to the surface, offers a possible solution to the
problem of measuring thin film mechanical properties. However, there are certain
inherent problemsin using nanoindentationtesting to examine the properties of thin
films. The problems stem in part from the presence of an interface between the film
and substrate. The quality of the interface can be affected by many variables, result-
ing in a range of effects on the apparent elastic and plastic properties of the film.
In particular, when the deformation region around the indent approaches the inter-
face, the indentation curve may exhibit features due to the thin film, the bulk, the
interface, or a combination of all three. As a direct consequence of these complica-
tions, models for thin-film behavior must attempt to take into account not only the
properties of the film and substrate, but also the interface between them.
If, initially, the effect of the interface is neglected, it is possible to divide thin-
coated systems into a number of categories that depend on the values of E (elastic
modulus) and Y (the yield stress) of the film and substrate. These categories are
typically [104,105]:
1. coatings with high E and high Y, substrates with high E and high Y;
2. coatings with high E and high Y, substrates with high or low E and low Y;
3. coatings with high or low E and low Y, substrates with high E and high Y;
4. coatings with high or low E and low Y, substrates with high orlow E and low Y.
The reasons for splitting thin film systems into these different categories have
been amply demonstrated experimentally by Whitehead and Page [104, 105] and
theoretically by Fabes et al. [106]. Essentially, hard, elastic materials(high E and Y)
will possess smaller plastic zones than soft, inelastic (low E and Y) materials. Thus,
when different combinations of materials are used as film and substrate, the overall
plastic zone will differ significantly. In some cases, the plasticity is confined to the
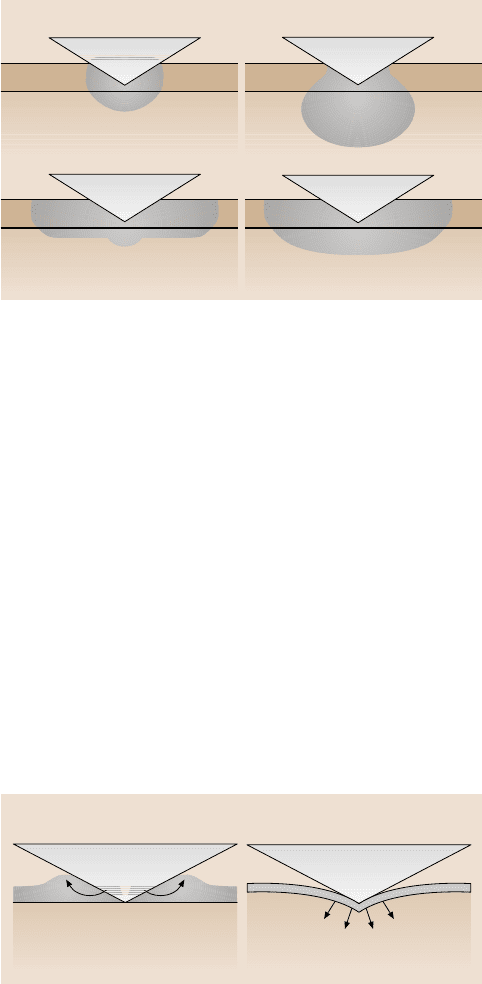
film, and in other cases, it is in both the film and substrate, as shown by Fig. 12.28.
If the standard nanoindentation analysis routines are to be used, it is essential that
t
he plastic zone and the elastic strain field are both confined to the film and do
not reach the substrate. Clearly, this is difficult to achieve unless extremely shallow
nanoindentations are used. There is an often quoted 10% rule, that says nanoin-
dents in a film must have a depth of less than 10% of the film’s thickness if only
the film properties are to be measured. This has no real validity [107]. There are
film/substrate combinations for which 10% is very conservative, while for other
combinations even 5% may be too deep. The effect of the substrate for different
combinations of film and substrate properties has been studied using FEM [108],
which has shown that the maximum nanoindentation depth to measure film only
properties decreases in moving from soft on hard to hard on soft combinations. For
a very soft film on a hard substrate, nanoindentations of 50% of the film thickness
are alright, but this drops to < 10% for a hard film on a soft substrate. For a very
12 Nanomechanical Properties of Solid Surfaces and Thin Films 641
a)
b)
c)
d)
Fig. 12.28. Variations in the plastic zone for indents on films and substrates of different prop-
erties. (a) Film and substrate have high E and Y,(b) film has a high E and Y, substrate has
ahighorlowE and low Y,(c) film has a high or low E and a low Y, and substrate has a high E
and Y,(d) film has a high or low E and a low Y, and substrate has a high or low E and a low Y
strong film on a soft substrate, the surface film behaves like an elastic membrane or
a bending plate.
Theoreticalanalysisof thin-filmmechanicalbehavioris difficult.One theoretical
approach that has been adopted uses the volumes of plastically deformed material
in the film and substrate to predict the overall hardness of the system. However, it
should be noted that this method is only really appropriate for soft coatings and in-
dentationdepths below the thicknessof the coating (see cases c and d of Fig. 12.28),
otherwise the behavior will be closer to that detailed later and shown by Fig. 12.29.
The technique of combining the mechanical properties of the film and substrate
to evaluate the overall hardness of the system is generally referred to as the rule of
mixtures. It stems from work by Burnett et al. [109–111] and Sargent [112], who
derived a weighted averageto relatethe “composite” hardness (H)tothevolumesof
plastically deformed material in the film (V
f
) and substrate (V
s
) and their respective
a)
b)
Fig. 12.29. Two different modes of deformation during nanoindentation of films. In (a)
materials move upwards and outwards, while in (b) the film acts like a membrane and the
substrate deforms

642 Adrian B. Mann
values of hardness, H
f
and H
s
. Thus,
H =
H
f
V
f
+ H
s
V
s
V
total
, (12.26)
where V
total
is V
f
+ V
s
.
Equation (12.26) was further developed by Burnett and Page [109] to take into
account the indentation size effect. They replaced H
s
with Kδ
n−2
c
,whereK and n
are experimentallydetermined constants dependent on the indenter and sample, and
δ
c
is the contact depth. This expression is derived directly from Meyer’s law for
spherical indentations, which gives the relationship P = Kd
n
between load, P,and
the indentation dimension, d. Burnett and Page also employed a further refinement
to enable the theory to fit experimentalresults from a specific sample, ion-implanted
silicon. This particular modification essentially took into account the different sizes
of the plastic zones in the two materials by multiplying H
s
by a dimensionlessfactor
(V
s
/V
total
). While this seems to be a sensible approach, it is mostly empirical, and
the physical justification for using this particular factor is not entirely clear. Later,
Burnett and Rickerby [110,111] took this idea further and tried to generalize the
equations to take into account all of the possible scenarios. Thus, the following
equations were suggested:
H =
H
f
Ω
3
V
f
+ H
s
V
s
V
total
, (12.27)
H =
H
f
V
f
+ H
s
Ω
3
V
s
V
total
. (12.28)
The first of these, (12.27), deals with the case of a soft film on a hard substrate,
and the second, (12.28), with a hard film on a soft substrate. The Ω term expresses
the variation of the total plastic zone from the ideal hemispherical shape. This was
taken still further by Bull and Rickerby [113], who derived an approximation for Ω
based on the film and substrate zone radii being related to their respective hardness
and elastic modulii [114,115]. Hence:
Ω =
(
E
f
H
s
/E
s
H
f
)
l
, (12.29)
where l is determined empirically. E
f
and H
f
and E
s
and H
s
are the elastic modulus
and hardness of the film and substrate, respectively.
Experimental data [116] indicate that the effect of the substrate on the elastic
modulus of the film can be quite different than the effect on hardness, due to the
zones of the elastic and plastic strain fields being different sizes.
Chechechin et al. [117] have recently studied the behavior of Al
2
O
3
films of
various thicknesses on different substrates. Their results indicate that many of the
models correctly predict the transition between the properties of the film and those
of the substrate, but do not always fit the observed hardness against depth curves.
This group have also studied the pop-in behavior of Al
2
O
3
films [118] and have
12 Nanomechanical Properties of Solid Surfaces and Thin Films 643
attempted to model the rangeof loads and depths at which they occur via a Weibull-
type distribution, as utilized in fracture analysis.
A point raised by Burnett and Rickerby should be emphasized. They state that
there are two very distinct modes of deformation during nanoindentation testing.
The first, referred to as Tabor’s [48] model for low Y/E materials, involves the
buildup of material at the side of the indenter through movement of material at
slip lines. The second, for materials with large Y/E does not result in surface pile-
up. The displaced material is then accommodated by radial displacements [115].
The point is that a thin, strong, and well-bonded surface film can cause a substrate
that would normally deform by Tabor’s method to behave more like a material with
high Y/E (see Fig. 12.29). It should be noted that this only applies as long as the
film does not fail.
In recent theoretical and experimental studies the importance of material pile-
up and sink-in has been investigated extensively. As discussed in an earlier section,
pile-up can be increased by residual compressive stresses, but even in the absence
of residual stresses pile-up can introduce a significant error in the calculated contact
area. This is most pronounced in materials that do not work-harden [62]. For these
materials using the Oliver and Pharr method fails to account for the pile-up and re-
sults in a large error in the values for E and H. For thin films Tsui et al. have used
a focused ion beam to section through Knoop indentations in both soft films on hard
substrates [69] and hard films on soft substrates [70]. The soft films, as expected,
exhibit pile-up, while the hard film acts more like a membrane and the indentation
exhibits sink-in with most of the plasticity in the substrate. Thus, there are three
clearly identifiable factors affecting the pile-up and sink-in around nanoindents dur-
ing testing of thin films:
1. Residual stresses
2. Degree of work-hardening
3. Ratio of film and substrate mechanical properties.
The bonding or adhesion between the film and substrate could also be added to
this list. And it should not be forgotten that the depth of the nanoindentation rela-
tive to the film thickness also affects pile-up. For a very deep nanoindentation into
a thin, soft film on a hard substrate pile-up is reduced, due to the combined con-
straints on the film of the tip and substrate [119]. Due to all of these complications,
using nanoindentation to study thin film mechanical properties is fraught with dan-
ger. Many unprepared researchers have misguidedly taken the values of E and H
obtained during nanoindentation testing to be absolute values only to find out later
that the values contain significant errors.
Many of the problems associated with nanoindentation testing are related to in-
correctly calculating the contact area, A.TheJoslin and Oliver method [71] is one
way that A can be removed from the calculations. This approach has been used with
some success to look at strained epitaxial II/VI semiconductor films [120], but there
is evidence that the lattice mismatch in these films can cause dramatic changes in
the mechanical properties of the films [121]. This may be due to image forces and
the film/substrate interface acting as a barrier to dislocation motion. Recently, it has

644 Adrian B. Mann
been shown that using films and substrates with known matching elastic moduli, it
is possible to use the assumption of constant elastic modulus with depth to evalu-
ate H [122]. In effect, this is using (12.1) to evaluate A from the contact stiffness
data, and then substituting the value for A into (12.12). The value of E is measured
independently, for instance, using acoustic techniques.
12.5.2 Multilayers
Multilayered materials with individual layers that are a micron or less in thickness,
sometimesreferred toas superlattices,can exhibitsubstantialenhancementsin hard-
ness or strength. This should be distinguished from the super modulus effect dis-
cussed earlier, which has been shown to be largely an artifact. The enhancements
in hardness can be as much as 100% when compared to the value expected from
the rule of mixtures, which is essentially a weighted average of the hardness for
the constituents of the two layers [123]. Table 12.1 shows how the properties of
isostructural multilayers can show a substantial increase in hardness over that for
fully interdiffused layers. The table also shows how there can be a substantial en-
hancement in hardness for non-isostructural multilayers compared to the values for
the same materials when they are homogeneous.
There are many factors that contribute to enhanced hardness in multilayers.
These can be summarized as [103]:
1. Hall-Petch behavior
2. Orowan strengthening
3. Image effects
4. Coherency and thermal stresses
5. Composition modulation
Hall-Petch behavior is related to dislocations piling-up at grain boundaries.
(Note that pile-up is used to describe two distinct effects: One is material build-
ing up at the side of an indentation, the other is an accumulation of dislocations on
Table 12.1. Results for some experimental studies of multilayer hardness
Study Multilayer Maximum hard- Reference Range of hard-
ness and multilayer hardness value ness values for
repeat length multilayers
Isostructural Cu/Ni 524 284 295–524
Knoop hardness [124] at 11.6 nm (interdiffused)
Non-isostructural Mo/NbN 33 GPa NbN – 17 GPa 12–33 GPa
Nanoindentation at 2 nm Mo – 2.7GPa
[125] Wo – 7 GPa
W/NbN 29 GPa (individual layer 23–29 GPa
at 3 nm materials)
12 Nanomechanical Properties of Solid Surfaces and Thin Films 645
a slip-plane.) The dislocation pile-upat grain boundariesimpedes the motion of dis-
locations. For materials with a fine grain structure there are many grain boundaries,
and, hence, dislocations find it hard to move. In polycrystalline multilayers, it is of-
ten the case that the size of the grains within a layer scales with the layer thickness
so that reducing the layer thickness reduces the grain size. Thus, the Hall-Petch re-
lationship (below) should be applicable to polycrystalline multilayer films with the
grain size, d
g
, replaced by the layer thickness.
Y = Y
0
+ k
HP
d
−0.5
g
, (12.30)
where Y is the enhanced yield stress, Y
0
is the yield stress for a single crystal, and
k
HP
is a constant.
There is an ongoing argument about whether Hall-Petch behavior really takes
place in nanostructured multilayers. The basic model assumes many dislocations
are present in the pile-up, but such large dislocation pile-ups are not seen in small
grains [126] and are unlikely to be present in multilayers. As a direct consequence,
studies have found a range of values, between 0 and −1, for the exponent in (12.30),
rather than the −0.5 predicted for Hall-Petch behavior.
Orowan strengthening is due to dislocations in layered materials being effec-
tively pinned at the interfaces. As a result, the dislocations are forced to bow out
along the layers. In narrow films, dislocations are pinned at both the top and bottom
interfaces of a layer and bow out parallel to the plane of the interface [127,128].
Forcing a dislocation to bow out in a layered material requires an increase in the
applied shear stress beyond that required to bow out a dislocation in a homoge-
neous sample. This additional shear stress would be expected to increase as the film
thickness is reduced.
Image effects were suggested by Koehler [129]as a possible source of enhanced
yield stress in multilayered materials. If two metals, A and B, are used to make
a laminate and one of them, A, has a high dislocation line energy, but the other, B,
has a low dislocation line energy, then there will be an increased resistance to dis-
location motion due to image forces. However, if the individual layers are thick
enough that there may be a dislocation source present within the layer, then dislo-
cations could pile-up at the interface. This will create a local stress concentration
point and the enhancement to the strength will be very limited. If the layers are thin
enough that there will be no dislocation source present, the enhanced mechanical
strength may be substantial. In Koehler’s model only nearest neighbor layers were
taken to contribute to the image forces. However, this was extended to include more
layers [130] without substantial changes in the results. The consequence on image
effects of reducing the thickness of the individual layers in a multilayer is that it
prevents dislocation sources from being active within the layer.
For many multilayer systems there is an increase in strength as the bilayer re-
peat length is reduced, but there is often a critical repeat length (e.g., 3nm for the
W/NbN multilayer of Table 12.1) below which the strength falls. One explanation
for the fall in strength involves the effects of coherency and thermal stresses on dis-
location energy. Unlike image effects where the energy of dislocations are a maxi-
mum or minimum in the center of layers, the energy maxima and minima are at the
