Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

626 Adrian B. Mann

a priori, (12.1) can be used to calculate the contact area, A, and, hence, you have

avalueforA

at a depth δ

. Repeating this procedure for a range of depths will give

a numerical version of the function A

(δ

). Then, it is simply a case of ﬁtting (12.15)

to the numerical data. If the hardness, H, is known and not a function of depth, and

the calibration specimen was fully plastic during testing, then essentially the same

approach could be used but based on (12.12). Situations where a constant H is used

to calibrate the tip are extremely rare.

In addition to the tip shape function, the machine compliance must be calibrated.

Basic Newtonian mechanics tells us that for the tip to be pushed into a surface the

tip must be pushing oﬀ of another body. During nanoindentation testing the other

body is the machine frame. As a result, during a nanoindentation test it is not just

the sample, but the machine frame that is being loaded. Consequently, a very small

elastic deformation of the machine frame contributes to the total stiﬀness obtained

from the unloading curve. The machine frame is usually very stiﬀ, > 10

N/m, so

the eﬀect is only important at relatively large loads.

To calibrate the machine frame stiﬀness or compliance, large nanoindentations

are made in a soft material such as aluminum with a known, isotropic elastic modu-

lus. For very deep nanoindentations made with a Berkovich pyramid, the contact

area, A

(δ

), can be reasonably approximated to 24.5δ

, thus (12.1) can be used to

ﬁnd the expected contact stiﬀness for the material. Any diﬀerence between the ex-

pected value of S and the value measured from the unloading curve will be due to

the compliance of the machine frame. Performing a number of deep nanoindenta-

tions enables an accurate value for the machine frame compliance to be obtained.

Currently, because of its ready availability and predictable mechanical proper-

ties, the most popular calibration material is fused silica (E = 72GPa, ν = 0.17),

though aluminum is still used occasionally.

12.3.6 Modiﬁcations to the Analysis

Since the development of the analysis routines in the early 1990s, it has become

apparent that the standard analysis of nanoindentation data is not applicable in all

situations, usually because errors occur in the calculated contact depth or contact

area. Pharr et al. [61–64] have used ﬁnite element modeling (FEM) to help under-

stand and overcome the limitations of the standard analysis. Two important sources

of errors have been identiﬁed in this way. The ﬁrst is residual stress at the sample

surface. The second is the change in the shape of nanoindents after elastic recovery.

The eﬀect of residual stresses at a surface on the indentationpropertieshas been

the subjectof debatefor manyyears [65–67]. The perceivedeﬀect wasthat compres-

sive stresses increased hardness, while tensile stresses decreased hardness. Using

FEM it is possible to model a pointed nanoindenter being pushed into a model ma-

terial that is in residual tension or compression. An FEM model of nanoindentation

into aluminumalloy 8009 [61] has conﬁrmed earlier experimentalobservations [68]

indicating that the contact area calculated from the unloading curve is incorrect if

there are residual stresses. In the FEM model of an aluminum alloy the mechanical

behavior of the material is modeled using a stress-strain curve, whichresembles that

12 Nanomechanical Properties of Solid Surfaces and Thin Films 627

Contact area A

Real contact area

O & P calculated contact area

Compression

Applied stress

Tension0

Fig. 12.16. When a surface is in a state of stress there is a signiﬁcant diﬀerence between the

contact area calculated using the Oliver and Pharr method and the actual contact area [61].

For an aluminum alloy this can lead to signiﬁcant errors in the calculated hardness and elastic

modulus

of an elastic-perfectly-plastic metal with a ﬂow stress of 425.6MPa. Yielding starts

at 353.1MPa and includes a small amount of work hardening. The FEM model was

used toﬁnd the contact areadirectly andusing the simulated unloadingcurvein con-

junction with Oliver and Pharr’s method. The results as a function of residual stress

are illustrated in Fig. 12.16. Note that the diﬀerences between the two measured

contact areas lead to miscalculations of E and H.

Errors in the calculated contact area stem from incorrect assumptions about the

pile-up and sink-in at the edge of the contact, as illustrated by Fig. 12.17.The Oliver

and Pharr analysis assumes the geometry of the sample surface is the same as that

given by Sneddon[47] in his analytical model for the indentation of elastic surfaces.

Clearly, for materials where there is signiﬁcant plastic deformation, it is possible

that there will be large deviations from the surface geometry found using Sneddon’s

elastic model. In reality, the error in the contact area depends on how much the

geometry of the test sample surface diﬀers from that of the calibration material

(typically fused silica). It is possible that a test sample, even without a residual

stress, will have a diﬀerent surface geometry and, hence, contact area at a given

depth, when compared to the calibration material. This is often seen for thin ﬁlms

Residual

compression

Sneddon’s

surface

profile

Residual

tension

Pile-up

Sink-in

Fig. 12.17. Pile-up and sink-

in are aﬀected by residual

stresses, and, hence, errors

are introduced into standard

Oliver and Pharr analysis

628 Adrian B. Mann

on a substrate (e.g., Tsui et al. [69, 70]). Residual stresses increase the likelihood

that the contact area calculated using Oliver and Pharr’s method will be incorrect.

The issue of sink-in and pile-up is always a factor in nanoindentation testing.

However, there is still no eﬀective way to deal with these phenomena other than

reverting to imaging of the indentations to identify the true contact area. Even this is

diﬃcult, as the edge of an indentation is not easy to identify using AFM or electron

microscopy. One approach that has been used [71] with some success is measuring

the ratio E

/H, ratherthan E

and H separately. Because E

is proportionalto 1/

√

and H is proportional to 1/A, E

/H should be independent of A and, hence, unaf-

fected by pile-up or sink-in. While this does not provide quantitative values for me-

chanical properties, it does provide a way to identify any variations in mechanical

properties with indentation depth or between similar samples with diﬀerent residual

stresses.

Another source of error in the Oliver and Pharr analysis is due to incorrect as-

sumptions about the nanoindentation geometry after unloading [63]. Once again,

this is due to diﬀerences between the test sample and the calibration material. The

exact shape of an unloaded nanoindentationon a material exhibiting elastic recovery

is not simply an impression of the tip shape; rather, there is some elastic recovery of

the nanoindentation sides giving them a slightly convex shape (see Fig. 12.18). The

shape actually dependson Poisson’s ratio, so the standard Oliver and Pharr analysis

will only be valid for a material where ν = 0.17, the value for fused silica, assuming

it is used for the calibration.

To deal with the variations in the recovered nanoindentation shape, it has been

suggested [63] that a modiﬁed nanoindenter geometry with a slightly concave side

be used in the analysis (see Fig. 12.18). This requires a modiﬁcation to (12.1):

S = γ2E



, (12.18)

where γ isa correctionterm dependenton thetip geometry.For aBerkovichpyramid

the best value is:

γ =

+ 0.15483073cotΦ



(1−2ν

)

4(1−ν

)





−0.83119312cotΦ



(1−2ν

)

4(1−ν

)



, (12.19)

Actual shape

Elastic recovery

of sides of indent

Expected shape

Modified

indenter

shape

Fig. 12.18. (a) Hay et al. [63]

found from experiments and

FEM simulations that the

actual shape of an indentation

after unloading is not as ex-

pected. (b) They introduced

a γ term to correct for this

eﬀect. This assumes the in-

denter has slightly concave

sides

12 Nanomechanical Properties of Solid Surfaces and Thin Films 629

Contact area (mm

)

3 u 10

2 u 10

1 u 10

Ideal Berkovich pyramid

O & P calculated area

Displacement (nm)

1,000500

γ corrected area

Fig. 12.19. For a real

Berkovich tip the γ corrected

area [63] is less at a given

depth than the area calculated

using the Oliver and Pharr

method

where Φ = 70.32

◦

. For a cube corner the correction can be even largerand γ is given

by:

γ = 1+



(1−2ν

)

4(1−ν

)tanΦ



, (12.20)

where Φ = 42.28

◦

. Figure 12.19 shows how the modiﬁed contact area varies with

depth for a real diamond Berkovich pyramid.

The validity of the γ-modiﬁed geometry is questionable from the perspective of

contact mechanics since it relies on assuming an incorrect geometry for the nanoin-

denter tip to correct for an error in the geometry of the nanoindentation impression.

The values for E and H obtained using the γ-modiﬁcation are, however, good and

can be signiﬁcantly diﬀerent to the values obtained with the standard Oliver and

Pharr analysis.

12.3.7 Alternative Methods of Analysis

All of the preceding discussion on the analysis of nanoindentation curves has fo-

cused on the unloading curve, virtually ignoring the loading curve data. This is for

the simple reason that the unloading curve can in many cases be regarded as purely

elastic, whereas the shape of the loading curve is determined by a complex mix of

elastic and plastic properties.

It is clear that there is substantially more data in the loading curve if it can be

extracted. Page et al. [57, 72] have explored the possibility of curve ﬁtting to the

loading data using a combination of elastic and plastic properties. By a combina-

tion of analysis and empirical ﬁtting to experimental data, it was suggested that the

loading curve is of the following form:

P = E

⎛

⎜

⎝



+ φ



⎞

⎟

⎠

−2

, (12.21)

where ψ and φ are determined experimentally to be 0.930 and 0.194, respectively.

For homogenoussamples this equation givesa linear relationshipbetween P and δ

630 Adrian B. Mann

Coatings, thin ﬁlm systems, and samples that strain-harden can give signiﬁcant de-

viations from linearity. Analysis of the loading curve has yet to gain popularity as

a standard method for examining nanoindentation data, but it should certainly be

regarded as a prime area for further investigation.

Another alternative method of analysis is based on the work involved in mak-

ing an indentation. In essence, the nanoindentation curve is a plot of force against

distance indicating integration under the loading curve will give the total work of

indentation, or the sum of the elastic strain energy and the plastic work of indenta-

tion.Integratingunder the unloadingcurveshouldgiveonlythe elastic strain energy.

Thus, the work involved in both elastic and plastic deformation during nanoinden-

tation can be found. Cheng and Cheng [73] combined measurements of the work of

indentation with a dimensional analysis that deals with the eﬀects of scaling in a ma-

terial that work-hardens to estimate H/E

. They subsequently evaluated H and E

using the Oliver and Pharr approach to ﬁnd the contact area.

12.3.8 Measuring Contact Stiﬀness

As discussed earlier, it is possible to add a small AC load on top of the DC load used

during nanoindentation testing, providing a way to measure the contact stiﬀness

throughoutthe entire loading and unloading cycle [74,75].The AC load is typically

at a frequency of ≈ 60Hz and creates a dynamic system, with the sample acting

as a spring with stiﬀness S (the contact stiﬀness), and the nanoindentation system

acting as a series of springs and dampers. Figure 12.20 illustrates how the small

AC load is added to the DC load. Figure 12.21 shows how the resulting dynamic

system can be modeled. An analysis of the dynamic system gives the following

relationships for S based on the amplitude of the AC displacement oscillation and

the phase diﬀerence between the AC load and displacement signals:

δ(ω)





−1

+ K

−mω



+ω

, (12.22)

tan(χ) =

ωD

−1

+ C

−1

+ K

−mω

, (12.23)

where C

is the load frame compliance (the reciprocal of the load frame stiﬀness),

is the stiﬀness of the support springs (typically in the region of 50–100N/m),

Load P

Displacement δ

Small, sinusoidal

AC load

Fig. 12.20. A small AC load can be added to the

DC load. This enables the contact stiﬀness, S ,to

be calculated throughout the indentation cycle

12 Nanomechanical Properties of Solid Surfaces and Thin Films 631

I/C

Fig. 12.21. The dynamic

model used in the analysis of

the AC response of a nanoin-

dentation device

D is the damping coeﬃcient, P

is the magnitude of the load oscillation, δ(ω)isthe

magnitude of the displacement oscillation, ω is the oscillation frequency, m is the

mass of the indenter, and χ is the phase angle between the force and the displace-

ment.

In order to ﬁnd S using either (12.22) or (12.23), it is necessary to calibrate

the dynamic response of the system when the tip is not in contact with a sample

−1

= 0). This calibration combined with the standard DC calibrations will provide

the values for all of the constants in the two equations.All that needs to be measured

in order to obtain S is either δ(ω)orχ, both of which are measured by the lock-in

ampliﬁerused to generate the AC signal. Sincethe S obtainedis the sameas the S in

(12.1),it followsthat the Oliverand Pharr analysis can be appliedto obtain E

and H

throughout the entire nanoindentation cycle.

The dynamic analysis detailed here was developedfor the MTS Nanoindenter™

(Oakridge, Tennessee), but a similar analysis has been applied to other commer-

cial instruments such as the Hysitron Triboscope™ (Minneapolis, Minnesota) [76].

For all instruments, an AC oscillation is used in addition to the DC voltage, and

a dynamic model is used to analyze the response.

12.3.9 Measuring Viscoelasticity

Using an AC oscillation in addition to the DC load introduces the possibility of

measuring viscoelastic properties during nanoindentation testing. This has recently

been the subject of considerable interest with researchers looking at the loss modu-

lus, storage modulus, and loss tangent of various polymeric materials [25, 77].

Recording the displacement response to the AC force oscillation enables the com-

plex modulus (including the loss and storage modulus) to be found. If the modulus

is complex, it is clear from (12.1) that the stiﬀness also becomes complex. In fact,

the stiﬀness will have two components: S



, the component in phase with the AC

force and S



, the component out of phase with the AC force.

The dynamic model illustrated in Fig. 12.21 is no longer appropriate for this

situation, as the contact on the test sample also includes a damping term, shown

in Fig. 12.22. Equations (12.22) and (12.23) must also be revised. Neglecting the

load frame compliance, C

, which in most real situations is negligible, (12.22) and

632 Adrian B. Mann

Fig. 12.22. The simpliﬁed

dynamic model used when

the sample is viscoelastic. It

is assumed that the load frame

compliance is negligible

(12.23) when the sample damping, D

, is included become:

(

)

S +K

−mω

+ω

(

D+D

)

, (12.24)

tan

(

)

(

D+ D

)

S + K

−mω

. (12.25)

In order to ﬁnd the loss modulus and storage modulus, (12.1) is used to relate S



(storage component) and S



(loss component) to the complex modulus.

This method for measuring viscoelastic properties using nanoindentation has

now been proven in principal, but has still only been applied to a very small range

of polymers and remains an area of future growth.

12.4 Modes of Deformation

As described earlier, the analysis of nanoindentation data is based ﬁrmly on the

results of elastic continuum mechanics. In reality, this idealized, purely elastic situ-

ation rarely occurs. For very shallow contacts on metals with thin surface ﬁlms such

as oxides, carbon layers, or organic layers [78,79], the contact can initially be very

similar to that modeled by Hertz and, later, Sneddon. It is very important to realize

that this in itself does not constitute proof that the contact is purely elastic, because

in many cases a small number of defects are present. These may be preexisting

defects that move in the strain-ﬁeld generated beneath the contact. Alternatively,

defects can be generated either when the contact is ﬁrst made or during the initial

loading [52, 80]. When defects such as short lengths of dislocation are present the

curves may still appear to be elastic even though inelastic processes like dislocation

glide and cross-slip are taking place.

12.4.1 Defect Nucleation

Nucleation of defects during nanoindentation testing has been the subject of many

experimental [81, 82] and theoretical studies [83, 84]. This is probably because

nanoindentation is seen as a way to deform a small, defect-free volume of material

12 Nanomechanical Properties of Solid Surfaces and Thin Films 633

to its elastic limit and beyond in a highly controlled geometry. There are, unfor-

tunately, problems in comparing experimental results with theoretical predictions,

largely because the kinetic processes involved in defect nucleation are diﬃcult to

model. Simulationsconducted at 0 K do not permit kinetic processes, and molecular

dynamics simulations are too fast (nanoseconds or picoseconds). Real nanoindenta-

tion experiments take place at ≈ 293K and last for seconds or even minutes.

Kinetic eﬀects appear in many forms, for instance, during the initial contact

between the indenter tip and the surface when defects can be generated by the com-

bined action of the impact velocity and surface forces [51]. A second example of

a kinetic eﬀect occurs during hold cycles at large loads when what appears to be

an elastic contact can suddenly exhibit a large discontinuity in the displacement

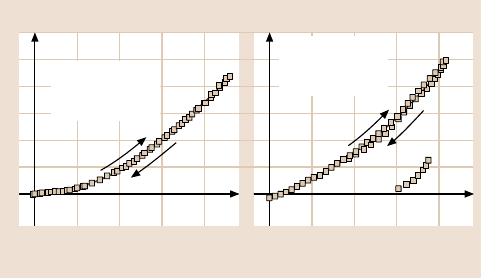
data [80]. Figure 12.23 shows how these kinetic eﬀects can aﬀect the nanoindenta-

tion data and the apparent yield point load.

During the initial formation of a contact, the deformation of surface asperi-

ties [51] and ledges [85] can create either point defects or short lengths of dislo-

cation line. During the subsequent loading, the defects can help in the nucleation

and multiplication of dislocations. The large strains present in the region surround-

ing the contact, coupled with the existence of defects generated on contact, can

result in the extremely rapid multiplication of dislocations and, hence, pronounced

discontinuities in the load-displacement curve. It is important to realize that the dis-

continuities are due to the rapid multiplication of dislocations, which may or may

not occur at the same time that the ﬁrst dislocation is nucleated. Dislocations may

have been present for some time with the discontinuity only occurring when the

existing defects are conﬁgured appropriately, as a Frank–Read source, for instance.

Even under large strains, the time taken for a dislocation source to form from preex-

isting defects may be long. It is, therefore, not surprising that large discontinuities

can be seen during hold cycles or unloading.

The generation of defects at the surface and the initiation of yielding is a com-

plex process that is extremely dependent on surface asperities and surface forces.

Load (mN)

Depth (nm)

100 203040

W (100)

Impact velocity

4 nm/s

Unloading

Load (mN)

Depth (nm)

100 203040

W (100)

Impact velocity

20 nm/s

Unloading

Fig. 12.23. Load-displacement curves for W(100) showing how changes in the impact veloc-

ity can cause a transition from perfectly elastic behavior to yielding during unloading

634 Adrian B. Mann

These, in turn, are closely related to the surface chemistry. It is not only the mag-

nitude of surface forces, but also their range in comparison to the height of surface

asperities that determines whether defects are generated on contact. Small changes

in the surface chemistry or the velocity of the indenter tip when it ﬁrst contacts the

surface, can cause a transition from a situation in which defects are generated on

contact to one where the contact is purely elastic [52].

When the generation of defects during the initial contact is avoided and the

deformed region under the contact is truly defect free, then the yielding of the sam-

ple should occur at the yield stress of a perfect crystal lattice. The load at which

plastic deformation commences under these circumstances becomes very repro-

ducible [86]. Unfortunately, nanoindenter tips on the near-atomic scale are not per-

fectly smooth or axisymmetric. As a result, accurately measuring the yield stress is

very diﬃcult. In fact, a slight rotation in the plane of the surface of either the sample

or the tip can give a substantial change in the observed yield point load. Coating the

surface in a cushioning self-assembled monolayer [87] can alleviate some of these

variations,but italso introducesa largeuncertainty in thecontact area.Surfaceoxide

layers, which may be several nanometersthick, have also been found to enhancethe

elastic behavior seen for very shallow nanoindentations on metallic surfaces [78].

Removal of the oxide has been shown to alleviate the initial elastic response.

While nanoindentation testing is ideal for examining the mechanical properties

of defect-free volumes and looking at the generation of defects in perfect crystal

lattices, it should be clear from the preceding discussion that great care must be

taken in examininghow the surface propertiesand the loading rate aﬀect the results,

particularly when comparisonsare being made to theoretical models for defect gen-

eration.

12.4.2 Variations with Depth

Ideal elastic-plastic behavior, as described by Tabor [48], can be seen during inden-

tation testing, provided the sample has been work-hardened so that the ﬂow stress

is a constant. However, it is often the case that the mechanical properties appear to

change as the load (or depth) is increased. This apparent change can be a result of

several processes, including work-hardening during the test. This is a particularly

important eﬀect for soft metals like copper. These metals usually have a high hard-

ness at shallow depths, but it decreases asymptotically with increasing indentation

depth to a hardness value that may be less than half that observed at shallow depths.

This type of behavior is due to the increasing density of geometrically necessary

dislocations at shallow depths [88]. Hence the eﬀects of work-hardening are most

pronounced at shallow depths. For hard materials the eﬀect is less obvious.

Work-hardening is one of the factors that contribute to the so-called indentation

size eﬀect (ISE), whereby at shallow indentation depths the material appears to be

harder. The ISE has been widely observed during microindentation testing, with at

least part of the eﬀect appearing to result from the increased diﬃculty in optically

measuring the area of an indentation when it is small. During nanoindentation test-

ing the ISE can also be observed, but it is often due to the tip area function, A

(δ

12 Nanomechanical Properties of Solid Surfaces and Thin Films 635

being incorrectly calibrated. However, there are physical reasons other than work-

hardening for expecting an increase in mechanical strength in small volumes. As

described in the previous section, small volumes of crystalline materials can have

either no defects or only a small number of defects present, making plastic yielding

more diﬃcult. Also, because of dislocation line tension, the shear stress required to

make a dislocation bow out increases as the radius of the bow decreases. Thus, the

shear stress needed to make a dislocation bow out in a small volume is greater than

it is in a largevolume. These physical reasons for small volumes appearing stronger

than large volumes are particularly important in thin ﬁlm systems, as will be dis-

cussed later. Note, however, that these physical reasons for increased hardness do

not apply for an amorphous material such as fused silica, which partially explains

its value as a calibration material.

12.4.3 Anisotropic Materials

The analysis methods detailed earlier were concerned primarily with the interpre-

tation of data from nanoindentations in isotropic materials where the elastic modu-

lus is assumed to be either independent of direction or a polycrystalline average

of a material’s elastic constants. Many crystalline materials exhibit considerable

anisotropy in their elastic constants, hence, these analysis techniques may not al-

waysbe appropriate.The theoreticalproblemof a rigidindenter pressedinto an elas-

tic, anisotropic half-space has been considered by Vlassak and Nix [89]. Their aim

was to identify the feasibility of interpreting data from a depth-sensing indentation

apparatus for samples with elastic constants that are anisotropic. Nanoindentation

experiments [90] have shown the validity of the elastic analysis for crystalline zinc,

copper, and beta-brass. The observed indentation modulus for zinc, as predicted,

varied by as much as a factor of 2 between diﬀerent orientations. The variations in

the observed hardness values for the same materials were smaller, with a maximum

variation with orientation of 20% detected in zinc. While these variations are clearly

detectable with nanoindentation techniques, the variations are small in comparison

to the actual anisotropy of the test material’s elastic properties. This is because the

indentation modulus is a weighted average of the stiﬀness in all directions.

At this time theeﬀects of anisotropy onthe hardness measuredusing nanoinden-

tation have not been fully explored. For materials with many active slip planes it is

likely that the small anisotropy observed by Vlassak and Nix is correct once plastic

ﬂow has been initiated. It is possible, however, that for defect-free crystalline speci-

mens with a limited number of active slip planes that very shallow nanoindentations

may show a much larger anisotropy in the observed hardness and initial yield point

load.

12.4.4 Fracture and Delamination

Indentation testing has been widely used to study fracture in brittle materials [91],

but the lower loads and smaller deformation regions of nanoindentation tests make