Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

7 Molecular Recognition Force Microscopy 283

For coupling to the tip surface and to the ligand, the crosslinker typically carries

two diﬀerent functional ends,e.g. an amine reactiveN-hydroxysuccinimidyl(NHS)

group on one end, and 2-pyridyldithiopropionyl (PDP) [18] or vinyl sulfone [19]

groups, which can be covalently bound to thiols, on the other (Fig. 7.2). This sulfur

chemistry is highly advantageous since it is very reactive and readily enables site-

directed coupling. However, free thiols are hardly available on native ligands and

must, therefore, be added.

Diﬀerent strategies have been used to achieve this goal. Lysine residues were

derivatizedwith the shortheterobifunctionallinkerN-succinimidyl-3-(S-acetylthio)-

propionate (SATP) [18]. Subsequent deprotection with NH

OH led to reactive SH

groups.Alternatively,lysinscan bedirectlycoupledvia aldehydegroups(manuscript

in preparation). A problem with the latter two methods is that they do not allow

for site-speciﬁc coupling of the crosslinker, since lysine residues are quite abun-

dant. Several protocols are commercially available (Pierce, Rockford, IL) to gen-

erate active antibody fragments with free cysteines. Half-antibodies are produced

by cleaving the two disulﬁde bonds in the central region of the heavy chain using

2-mercaptoethylamine HCl [20] and Fab fragments are generated from papain di-

gestion [11]. The most elegant methods are to introduce a cysteine into the primary

sequence of proteins or to append a thiol group to the end of a DNA strand [6], al-

lowing for awell-deﬁnedsequence-speciﬁccoupling of theligand to the crosslinker.

An attractive alternative for covalent coupling is provided by the widely used

nitrilotriacetate (NTA)-His

system. The strength of binding in this system, which

is routinely used in chromatographic and biosensor matrices, is signiﬁcantly larger

than that between most ligand–receptor pairs [21–23]. Since a His

tag can be read-

ily appended to proteins, a crosslinker containing an NTA residue is ideally suited

for coupling proteins to the AFM tip. This generic, site-speciﬁc coupling strat-

egy also allows rigorous and ready control of binding speciﬁcity by using Ni

as a molecular switch of the NTA-His

bond.

7.3 Immobilization of Receptors onto Probe Surfaces

To enable force detection, the receptors recognized by the ligand-functionalizedtip

need to be ﬁrmly attached to the probed surface. Loose association will unavoidably

lead to a pull-oﬀ of the receptors from the surface by the tip-immobilized ligands,

precluding detection of the interaction force.

Freshly cleaved muscovite mica is a perfectly pure and atomically ﬂat surface

and, therefore, ideally suited for MRFMtudies. The strong negative charge of mica

also accomplishes very tight electrostatic binding of various biomolecules. For ex-

ample, lysozyme [20] and avidin [24] strongly adhere to mica at pH < 8. In such

cases, simple adsorption of the receptors from the solution is suﬃcient, since attach-

ment is strong enough to withstand pulling. Nucleic acids can also be ﬁrmly bound

to mica through mediatory divalent cations such as Zn

,Ni

or Mg

[25]. The

strongly acidic sarcoplasmic domain of the skeletal-muscle calcium-releasechannel

(RYR1) was likewise absorbed to mica via Ca

bridges [26]. Carefully optimizing

284 Peter Hinterdorfer and Ziv Reich

buﬀer conditions, similar strategies were used to deposit protein crystals and bacte-

rial layers onto mica in deﬁned orientations [27,28].

The use of nonspeciﬁc electrostatic-mediated binding is however quite limited

and generally oﬀers no means to orient the molecules over the surface in a desirable

direction. Immobilization through covalent attachment must therefore be frequently

explored. When glass, silicon or mica are used as probe surfaces, immobilization

is essentially the same as described above for tip functionalization. The number of

reactive SiOH groups of the chemically relatively inert mica can optionally be in-

creasedby waterplasma treatment[29].As with tips, crosslinkersare also often used

to provide receptors with motional freedom and to prevent surface-induced protein

denaturation [4]. Immobilization can be controlled, to some extent, by using pho-

toactivatable crosslinkers, such as N-5-azido-2-nitrobenzoyloxysuccinimide[30].

A major limitation of silicon chemistry is that it does not allow for high surface

densities, i.e., > 1000/µm

. By comparison, the surface density of a monolayer of

streptavidin is about 60,000 molecules per µm

and that of a phospholipid mono-

layer may exceed 10

molecules per µm

. The latter high density is also achievable

by chemisorption of alkanethiols to gold. Tightly bound functionalized alkanethiol

monolayersformed on ultraﬂat gold surfaces provideexcellentprobes for AFM [10]

and readily allow for covalentand non-covalentattachmentof biomolecules[10,31]

(Fig. 7.3).

Recently, Kada et al. [32] reported on a new strategy to immobilize pro-

teins on gold surfaces using phosphatidyl choline or phosphatidyl ethanolamine

analogues containing dithio-phospholipids at their hydrophobic tail. Phosphatidyl

100 nm

0 10 nm

Fig. 7.3. AFM image of his-

RNAP molecules speciﬁcally

bound to nickel-NTA do-

mains on a functionalized

gold surface. Alkanethiols

terminated with ethylene gly-

col groups to resist unspeciﬁc

protein adsorption served as

a host matrix and were doped

with 10% nickel-NTA alken-

thiols. The sample was pre-

pared to achieve full mono-

layer coverage. Ten individ-

ual hisRNAP molecules can

be clearly visualized bound

to the surface. The more

abundant, smaller, lower fea-

tures are NTA islands with

no bound molecules. The un-

derlying morphology of the

gold can also be distinguished

(after [31])

7 Molecular Recognition Force Microscopy 285

ethanolamine, which is chemically reactive, was derivatized with a long-chain bi-

otin for the molecular recognition of streptavidin molecules in an initial study [32].

These self-assembled phospholipid monolayers closely mimic the cell surface and

minimize nonspeciﬁc adsorption. Additionally, they can be spread as insoluble

monolayers at an air/water interface. Thereby, the ratio of functionalized thio-lipids

to host lipids accurately deﬁnes the surface density of bioreactive sites in the mono-

layer. Subsequent transfer onto gold substrates leads to covalent and, hence, tight

attachment of the monolayer.

MRFMas also been used to study the interactions between ligands and cell sur-

face receptors in situ, on ﬁxed or unﬁxed cells. In these studies it was found that

the immobilization of cells strongly depends on cell type. Adherent cells are read-

ily usable for MRFMhereas cells that grow in suspension need to be adsorbed onto

the probe surface. Various protocols for tight immobilization of cells over a surface

are available. For adherent cells, the easiest way is to grow the cells directly on

glass or other surfaces suitable for MRFM [33]. Firm immobilization of non- and

weakly adhering cells can be achieved by various adhesive coatings such as Cell-

Tak [34], gelatin, or polylysine. Hydrophic surfaces like gold or carbon are also

very useful to immobilize non-adherent cells or membranes [35]. Covalent attach-

ment of cells to surfaces can be accomplished by crosslinkers that carry reactive

groups, such as those used for immobilization of molecules [34]. Alternatively, one

can use crosslinkers carrying a fatty-acid moiety that can penetrate into the lipid bi-

layer of the cell membrane. Such linkers provide suﬃciently strong ﬁxation without

interference with membrane proteins [34].

7.4 Single-Molecule Recognition Force Detection

Measurements of interaction forces traditionally rely on ensemble techniques such

as shear ﬂow detachment (SFD) [36] and the surface force apparatus (SFA) [37]. In

SFD, receptors are ﬁxed to a surface to which ligands carried by beads or presented

on the cell surface bind speciﬁcally. The surface-bound particles are then subjected

to a ﬂuid shear stress that disrupts the ligand–receptor bonds. However, the force

acting between single molecular pairs can only be estimated because the net force

applied to the particles can only be approximated and the number of bonds per

particle is unknown.

SFA measures the forces between two surfaces to which diﬀerent interacting

molecules are attached using a cantilever spring as a force probe and interferometry

for detection. The technique, which has a distance resolution of ≈ 1 Å, allows one

to measure adhesive and compressive forces and to follow rapid transient eﬀects in

real time. However, the force sensitivity of the technique (≈ 10 nN) does not allow

for single-molecule measurements of non-covalentinteraction forces.

The biomembraneforceprobe (BFP) techniqueuses pressurized membranecap-

sules rather than mechanical springs as the force transducer (Fig. 7.4; for a recent

paper see [38]). To form the transducer, a red blood cell or a lipid bilayer vesicle

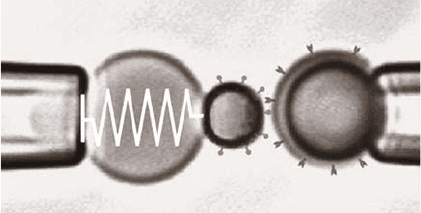
286 Peter Hinterdorfer and Ziv Reich

Fig. 7.4. Experimental set-up of the biomembrane force probe (BFP). The spring in the BFP

is a pressurized membrane capsule. Its spring constant is set by membrane tension, which is

controlled by micropipette suction. The BFP tip is formed by a glass microbead with a diam-

eter of 1–2 µm chemically glued to the membrane. The BFP (on the left) was kept stationary

and the test surface, formed by another microbead (on the right), was translated to or from

contact with the BFP tip by precision piezo control (after [38])

is pressurized into the tip of a glass micropipette. The spring constant of the cap-

sule can then be varied over several orders of magnitude by suction. This simple,

but highly eﬀective conﬁguration, enables the measurement of forces ranging from

0.1pN to 1000pN with a force resolution of about 1pN, allowing probing of single

molecular bonds.

Optical tweezers (OT) belong to a family of techniques that rely on external

ﬁelds to manipulate single particles. Thus, unlike mechanical transducers, force

is exerted from a distance. In optical tweezers (OT), small particles (beads) are

manipulated by optical traps [39]. Three-dimensional light-intensity gradients of

a focused laser beam are used to pull or push particles with positional accuracy of

a few nanometers. Using this technique, forces in the range of 10

−13

–10

−10

N can

accurately be measured. Optical tweezers have been used extensively to measure

the force-generating properties of various molecular motors at the single-molecule

level [40] and to obtain force-extension proﬁles of single DNA [41] or protein [42]

molecules. Deﬁned, force-controlled twisting of DNA using rotating magnetically

manipulated particles gave even further insights into DNA viscoelastic proper-

ties [43].

The atomic force microscope (AFM; [1]) is the force-measuring method with

the smallest force sensor and therefore provides the highest lateral resolution. Radii

of commercially available AFM tips vary between 2 and 50 nm. In contrast, the

particles used for force sensing in SFD, BFP, and OT are in the 1–10µm range, and

the surfaces used in SFA exceed millimeter extensions. The small apex of the AFM

tip allows the visualization of single biomolecules with molecular to submolecular

resolution [25,27,28].

In addition to imaging, AFM has successfully been used to measure interaction

forces between various single molecular pairs [2–4]. In these measurements, one

of the binding partners is immobilized onto a tip mounted at the end of a ﬂexible

cantilever that functions as a force transducer and the other is immobilized over

7 Molecular Recognition Force Microscopy 287

12345

10 nm

0.2 nN

Fig. 7.5. Single-molecule recognition event detected with AFM. A force–distance cycle,

measured with and amplitude of 100 nm at a sweep frequency of 1 Hz, for an antibody anti-

gen pair in PBS. Binding of the antibody immobilized on the tip to the antigen on the surface,

which occurs during the approach (trace points 1 to 5), results in a parabolic retract force

curve (points 6 to 7) reﬂecting the extension of the distensible crosslinker antibody antigen

connection. The force increases until unbinding occurs at a force of 268 pN (points 7 to 2)

(after [4])

a hard surface such as mica or glass. The tip is initially broughtto, and subsequently

retracted from the surface, and the interaction (unbinding) force is measured by fol-

lowing the cantilever deﬂection, which is monitored by measuring the reﬂection of

a laser beam focused on the back of the cantilever using a split photodiode. Ap-

proach and retract traces obtained from the unbinding of a single molecular pair are

shown in Fig. 7.5 [4]. In this experiment, the binding partners were immobilized

onto their respective surfaces through a distensible PEG tether.

Cantilever deﬂection, Δx, relates directly to the force F, acting on it directly

throughHook’s law F = kΔx,wherek is thespring constant of the cantilever. During

most of the approach phase (trace, and lines 1 to 5), when the tip and the surface are

suﬃciently far away from each other (1 to 4), cantilever deﬂection remains zero be-

cause themolecules areas yet unboundto each other. Uponcontact (4) thecantilever

bends upwards (4 to 5) due to a repulsive force that increases linearly as the tip is

pushed further into the surface. If the cycle was futile, and no binding had occurred,

retraction of the tip from the surface (retrace, 5 to 7) will lead to a gradualrelaxation

of the cantilever to its rest position (5 to 4). In such cases, the retract curve will look

very much like the approach curve. On the other hand, if binding had occurred, the

cantilever will bend downwards as the cantilever is retracted from the surface (re-

288 Peter Hinterdorfer and Ziv Reich

trace, 4 to 7). Since the receptor and ligand were tethered to the surfaces through

ﬂexible crosslinkers, the shape of the attractive force–distance proﬁle is nonlinear,

in contrast to the proﬁle obtained during contact (4 to 7). The exact shape of the

retract curve depends on the elastic properties of the crosslinker used for immobi-

lization [17,44] and exhibits parabolic-like characteristics, reﬂecting an increase of

the spring constant of the crosslinker during extension. The downward bending of

the retracting cantilever continues until the ramping force reaches a critical value

that dissociates the ligand–receptor complex (unbinding force, 7). Unbinding of the

complex is indicated by a sharp spike in the retract curve that reﬂects an abrupt

recoil of the cantilever to its rest position. Speciﬁcity of binding is usually demon-

strated by block experiments in which free ligands are added to mask receptor sites

over the surface.

The force resolution of the AFM, ΔF = (k

Tk)

1/2

, is limited by the thermal

noise of the cantilever which, in turn, is determined by its spring constant. A way

to reduce thermal ﬂuctuations of cantilevers without changing their stiﬀness or low-

ering the temperature is to increase the apparent damping constant. Applying an

actively controlled external dissipative force to cantilevers to achieve such an in-

crease, Liang et al. [45] reported a 3.4-fold decrease in thermal noise amplitude.

The smallest forces that can be detected with commercially available cantilevers are

in the few piconewton range. Decreasing cantilever dimensions enables one to push

the range of detectable forces to smaller forces since small cantilevers have lower

coeﬃcients of viscous damping [46]. Such miniaturized cantilevers also have much

higher resonance frequencies than conventional cantilevers and, therefore, allow for

faster measurements.

Besides the detectionof intermolecularforces, the AFM also shows great poten-

tial in measuring forces acting within molecules. In these experiments, the molecule

is clamped between the tip and the surface and its viscoelastic properties are studied

by force–distance cycles.

7.5 Principles of Molecular Recognition Force Spectroscopy

Molecular recognition is mediated by a multitude of non-covalent interactions the

energy of which is only slightly higher than thermal energy. Due to the power law

dependence of these interactions on the distance, the attractive forces between non-

covalently interacting molecules are extremely short-ranged. A close geometrical

and chemical ﬁt within the binding interface is therefore a prerequisite for produc-

tive association. The weak bonds that govern molecular cohesion are believed to

be formed in a spatially and temporarily correlated fashion. Protein binding often

involves structural rearrangements that can be either localized or global. These re-

arrangements often bear functional signiﬁcance by modulating the activity of the

interactants. Signaling pathways, enzyme activity, and the activation and inactiva-

tion of genes all depend on conformational changes induced in proteins by ligand

binding.

7 Molecular Recognition Force Microscopy 289

The strength of binding is usually given by the binding energy E

,which

amounts to the free-energy diﬀerence between the bound and the free state, and

which can readily be determined by ensemble measurements. E

determines the ra-

tio of bound complexes [RL] to the product of free reactants [R][L] at equilibrium

and is related to the equilibrium dissociation constant K

through E

= −RT ln(K

where R is the gas constant. K

itself is related to the empirical association (k

)and

dissociation (k

oﬀ

) rate constants through K

= k

oﬀ

. In order to get an estimate

for the interaction forces, f, from the binding energies E

, the depth of the bind-

ing pocket may be used as a characteristic length scale l. Using typical values of

= 20k

T and l = 0.5 nm, an order-of-magnitudeestimate of f(= E

/l) ≈ 170pN

is obtained for the binding strength of a single molecular pair. Classical mechanics

describes bond strength as the gradient in energy along the direction of separation.

Unbinding therefore occurs when the applied force exceeds the steepest gradient in

energy. This purely mechanical description of molecular bonds, however, does not

provide insights into the microscopic determinants of bond formation and rupture.

Non-covalent bonds have limited lifetimes and will therefore break even in the

absenceofexternalforce on characteristictime scales neededfor spontaneousdisso-

ciation (τ(0) = k

−1

oﬀ

). Pulled faster than τ(0), however, bonds will resist detachment.

Notably, the unbinding force may approach and even exceed the adiabatic limit

given by the steepest energy gradient of the interaction potential, if rupture occurs

in less time than needed for diﬀusive relaxation (10

−10

–10

−9

s for biomolecules in

viscousaqueous medium)and friction eﬀects become dominant[48]. Therefore,un-

binding forces do not resemble unitary values and the dynamics of the experiment

critically aﬀects the measured bond strengths. At the time scale of AFM experi-

ments (milliseconds to seconds), thermal impulses govern the unbinding process.

In the thermal activation model, the lifetime of a molecular complex in solution is

described by a Boltzmann ansatz, τ(0) = τ

osc

exp(E

T) [49], where τ

osc

is the

inverse of the natural oscillation frequencyand E

is the height of the energy barrier

for dissociation. This gives a simple Arrhenius dependency of dissociation rate on

barrier height.

A force acting on a complex deforms the interaction free-energy landscape and

lowers barriers for dissociation (Fig. 7.6). As a result of the latter, bond lifetime is

shortened. The lifetime τ(f) of a bond loaded with a constant force f is given by:

τ(f) = τ

osc

exp[(E

− x

f)/k

T] [49], where x

marks the thermally averaged pro-

jection of the energy barrier along the direction of the force. A detailed analysis of

the relation between bond strength and lifetime was performed by Evans et al. [50],

using Kramers’theory for overdamped kinetics. For a sharp barrier,the lifetime τ(f)

of a bond subjected to a constant force f relates to its characteristic lifetime, τ(0),

according to: τ(f) = τ(0)exp(−x

f/k

T) [4]. However, in most pulling experiments

the appliedforceis not constant. Rather,it increasesin a complex,nonlinear manner,

which depends on the pulling velocity, the spring constant of the cantilever, and the

force–distanceproﬁle of the molecular complex. Nevertheless,contributions arising

from thermal activation manifest themselves mostly near the point of detachment.

Therefore, the change of force with time or the loading rate r(= df/ dt) can be de-

290 Peter Hinterdorfer and Ziv Reich

Fig. 7.6. Dissociation over

a single sharp energy barrier.

Under a constant force, the

barrier is lowered by the ap-

plied force F.Thisgivesrise

to a characteristic length scale

that is interpreted as the

distance of the energy barrier

from the energy minimum

along the projection of the

force (after [47])

rived from the product of the pulling velocity and the eﬀectivespring constant at the

end of the force curve, just before unbinding occurs.

The dependence of the rupture force on the loading rate (force spectrum), in the

thermally activatedregime was ﬁrstderivedby Evansand Ritchie [50] and described

further by Strunz et al. [47]. Forced dissociation of receptor ligand complexes using

AFM or BFP can often be regardedas an irreversible process because the molecules

are kept moving away from each other after unbinding had occurred (rebinding can

be safely neglected when measurements are made with soft springs). Rupture itself

is a stochastic process and the likelihood of bond survival is expressed in the master

equation as a time-dependentprobability N(t) to be in the bound stateunder a steady

ramp of force, namely dN(t)/ dt = −k

oﬀ

(rt)N(t) [47]. This results in a distribution

of unbinding forces P(F) parameterized by the loading rate [47,50, 51]. The most

probable force for unbinding f

∗

, given by the maximum of the distribution, relates

to the loading rate through f

∗

= f

ln(rk

−1

oﬀ

/ f

), where the force scale f

is set by

the ratio of thermal energy to x

[47,50]. Thus, the unbinding force scales linearly

with the logarithm of the loading rate. For a single barrier, this would give rise to

a simple, linear force spectrum f

∗

versus log(r). In cases where the escape path is

traversed by several barriers, the curve will follow a sequence of linear regimes,

each marking a particular barrier [38, 50, 51]. Transition from one regime to the

other is associated with an abrupt change of slope determined by the characteristic

barrier length scale and signifying that a crossover between barriers has occurred.

Dynamic force spectroscopy (DFS) exploits the dependence of bond strength

on the loading rate to obtain detailed insights into intra- and intermolecular interac-

tions. By measuring bond strength over a broad range of loading rates, length scales

and relativeheights ofenergy barrierstraversingthe free-energysurfacecan be read-

ily obtained. The lifetime of a bond at any given force is likewise contained in the

complete force distribution [4]. Finally, one may attempt to extract dissociation rate

constants by extrapolation to zero force [52]. However, the application of force acts

to select the dissociation path. Since the kinetics of reactionsis pathway-dependent,

7 Molecular Recognition Force Microscopy 291

such a selection implies that kinetic parameters extracted from force-probe experi-

ments may diﬀer from those obtained from assays conducted in the absence of ex-

ternal force. Under extremely fast complexation/decomplexationkinetics the forces

can be independent of the loading rate, indicating that the experiments were carried

out under thermodynamic equilibrium [53].

7.6 Recognition Force Spectroscopy:

From Isolated Molecules to Biological Membranes

7.6.1 Forces, Energies, and Kinetic Rates

Conductedat ﬁxedloading rates,pioneeringmeasurementsof interactionforcesrep-

resent single points in continuous spectra of bond strengths [38]. Not unexpectedly,

the ﬁrst interaction studied was that between biotin and its extremely high-aﬃnity

receptors avidin [3] and streptavidin [2]. The unbinding forces measured for these

interactions were 250–300 pN and 160pN for streptavidin and avidin, respectively.

During this initial phase it was also revealed that diﬀerent unbinding forces can be

obtained for the same pulling velocity if the spring constant of the cantilever is var-

ied [2],which is consistent with the aforementioneddependencyof bondstrength on

the loading rate. The interaction force between several biotin analogues and avidin

or streptavidin [54] and between biotin and a set of streptavidin mutants [55] was

investigated and found generally to correlate with the equilibrium binding enthalpy

and the enthalpic activation barrier. No correlation with the equilibrium free energy

of binding or the activation free-energy barrier to dissociation was observed, sug-

gesting that internal energies rather than entropic contributions were probed by the

force measurements [55].

In another pioneering study, Lee et al. [6] measured the forces between comple-

mentary 20-base DNA strands covalently attached to a spherical probe and surface.

The interaction forces fell into three diﬀerent distributions amounting to the rup-

ture of duplexes consisting of 12, 16, and 20 base pairs. The average rupture force

per base pair was ≈ 70 pN. When a long, single-stranded DNA was analyzed, both

intra- and interchain forces were observed, the former probing the elastic properties

of the molecule. Hydrogen bonds between nucleotides have been probed for all 16

combinationsof the four DNA bases [7]. Directional hydrogen-bondinginteractions

were measured only when complementary bases were present on the tip and probe

surfaces,indicating that AFM can be used to follow speciﬁcpairing of DNA strands.

Strunz et al. [15] measured the forces required to separate individual double-

stranded DNA molecules of 10, 20, and 30 base pairs (Fig. 7.7). The parameters

describing the energy landscape, i.e., the distance of the energy barrier from the

minimum energy along the separation path and the logarithm of the thermal disso-

ciation rate, were found to be proportional to the number of base pairs of the DNA

duplex. Such scaling suggests that unbinding proceeds in a highly cooperativeman-

ner characterized by one length scale and one time scale. Studying the dependence

of rupture forces on the temperature, it was proposed by Schumakovitch et al. [56]

292 Peter Hinterdorfer and Ziv Reich

Force (pN)

Velocity (nm/s)

–10

–5

Probability

Force (pN)

0.15

0.10

0.05

0.00

06020 40 80

a) b)

30 bp

20 bp

10 bp

1600 nm/s

8 nm/s

Fig. 7.7. Dependence of the unbinding force between DNA single-strand duplexes on the

retract velocity. In addition to the expected logarithmic behavior on the loading rate, the

unbinding force scales with the length of the strands, increasing from the 10- to 20- to 30-

base-pair duplexes (after [15])

that entropic contributions play an important role in the unbinding of complemen-

tary DNA strands [56].

Prevalentas it is, molecular recognition has mostly been discussed in the context

of the interactions betweenantibodies and antigens. To maximize motional freedom

and to overcome problems associated with misorientation and steric hindrance, an-

tibodies and antigens were immobilized onto AFM tip and probe surfaces via ﬂex-

ible molecular spacers [4, 10,13, 14]. Optimizing antibody density over the AFM

tip [4,12], the interaction between individual antibody antigen pairs could be ex-

amined. Binding of antigen to the two Fab fragments of the antibody was shown to

occur independentlyand with equal probability.Single antibody antigenrecognition

events were also recorded with tip-bound antigens interacting with intact antibod-

ies [10,13] or with single-chain wild-type (Fv) fragments [14]. The latter study also

showed that an Fv mutant whose aﬃnity to the antigen was attenuated by about 10

folds dissociated from the antigen under applied forces that were 20% lower than

those required to unbind the wild-type (Fv) antibody.

Besides measurementsof interaction forces, single-molecule force spectroscopy

also allows estimation of association and dissociation rate constants with the con-

cern stated above withstanding [4,12,22,52,57,58],and measurement of structural

parameters of the binding pocket [4, 12,15, 57,58]. Quantiﬁcation of the associa-

tion rate constant k

requires determination of the interaction time needed for half-

maximal probability of binding (t

1/2

). This can beobtained from experimentswhere

the encounter time between receptor and ligand is varied over a broad range [57].

Given that the concentration of ligand molecules on the tip available for interaction

with the surface-bound receptors c

eﬀ

is known, the association rate constant can be

derived from k

= t

−1

0.5

−1

eﬀ

. Determination of the eﬀective ligand concentration re-

quires knowledge of the eﬀective volume V

eﬀ

explored by the tip-tethered ligand