Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

262 A. Schirmeisen et al.

conditions have been reported so far. Interestingly, a low-budget construction set

(employing a tuning-fork force sensor) for a CE-mode dynamic AFM set-up has

been published on the internet (http://www.sxm4.uni-muenster.de).

If it is possible to measure atomic scale forces with the NC-AFM, it should

vice versa also be possible to exert forces with a similar precision. In fact, the new

and exciting ﬁeld of nanomanipulation could be driven to a whole new dimension,

if deﬁned forces can be reliably applied to single atoms or molecules. In this re-

spect, Loppacher et al. [47] were able to push on diﬀerent parts of an isolated Cu-

tetrabromobisphenol (TBBP) molecule, which is known to possess four rotatable

legs. They measured the force–distance curves while pushing one of the legs with

the AFM tip. From the force curves they we able to determine the energy which

was dissipated during the switching process of the molecule. The manipulation of

single silicon atoms with NC-AFM was demonstrated by Oyabu et al. [48], who

removed single atoms from a Si(111)-7×7 surface with an AFM tip and could sub-

sequently deposit atoms from the tip onto the surface again. The possibility to exert

and measure forces simultaneously during single-atom or molecule manipulation is

an exciting new application of high-resolution NC-AFM experiments.

6.4 Q-Control

We have already discussed the virtues of a high Q value for high-sensitivity meas-

urements: the minimum detectable force gradient was inversely proportional to the

square root of Q. In vacuum, Q mainly represents the internal dissipation of the can-

tilever during oscillation, an internal damping factor. Low damping is obtained by

using high-quality cantilevers, which are cut (or etched) from defect-free single-

crystal silicon wafers. Under ambient or liquid conditions, the quality factor is

dominated by dissipative interactions between the cantilever and the surrounding

medium, and Q values can be as low as 100 for air or even 5 in liquid. Still, we

ask if it is somehow possible to compensate for the damping eﬀect by exciting the

cantilever in a sophisticated way?

It turns out that the shape of the resonance curves in Fig. 6.5 can be inﬂuenced

towards higher (or lower) Q values by an amplitude feedback loop. In principle,

there are several mechanisms to couple the amplitude signal back to the cantilever,

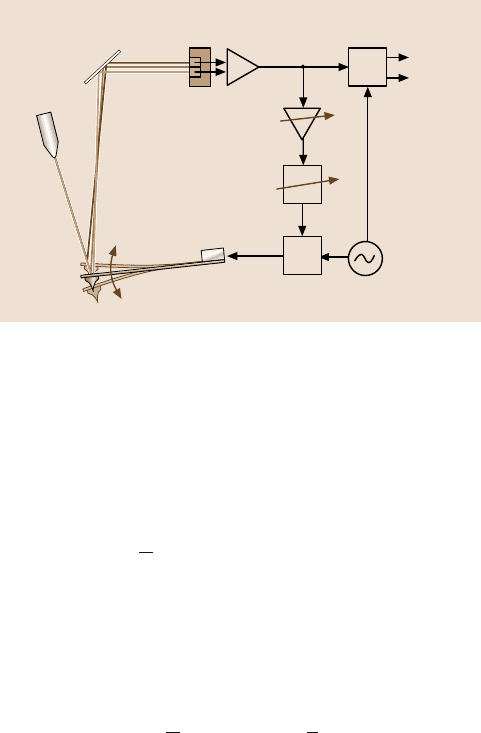
e.g., by the photothermal eﬀect [49] or capacitive forces [50]. Figure 6.19 shows

a method in which the amplitude feedback is mediated directly by the excitation

piezo [51]. This has the advantage that no additional mechanical setups are neces-

sary.

The working principle of the feedback loop can be understood by analyzing the

equation of motion of the modiﬁed dynamic system:

∗

¨z(t)+ α˙z(t)+ kz(t)−F

+ z(t)) = F

ext

cos(ωt)+ Ge

iφ

z(t). (6.26)

This ansatz takes into account the feedback of the detector signal through a phase

shifter, ampliﬁer and adder as an additional force, which is linked to the cantilever

6 Dynamic Modes of Atomic Force Microscopy 263

Laser

Detector

Mirror

Lock-in

amplifier

Piezo

Adder

Cantilever

+ tip

Detector signal

Variable

phase shifter

Function

generator

Variable

gain amplifier

Phase

Amplitude

Fig. 6.19. Schematic diagram of operating a Q-control feedback circuit with an externally

driven dynamic AFM. The tapping-mode set-up is in eﬀect extended by an additional feed-

back loop

deﬂection z(t) through the gain G and the phase shift e

iφ

. We assume that the oscil-

lation can be described by a harmonic oscillation trajectory. With a phase shift of

φ = ±π/2 we ﬁnd:

±iπ/2

z(t) = ±

˙z(t). (6.27)

This means, that the additional feedback force signal Ge

iφ

z(t) is proportional to the

velocity of the cantilever, just like the damping term in the equation of motion. We

can deﬁne an eﬀective damping constant α

eﬀ

, which combines the two terms:

∗

¨z(t)+ α

eﬀ

˙z(t)+ kz(t)−F

+ z(t)) = F

ext

cos(ωt), (6.28)

with α

eﬀ

= α ±

G for φ = ±

Equation (6.28) shows that the damping of the oscillator can be enhanced or weak-

ened by choosing φ =+π/2orφ = −π/2, respectively. The feedback loop there-

fore allows us to vary the eﬀective quality factor Q

eﬀ

= mω

/α

eﬀ

of the complete

dynamic system. Hence, this system was termed c-Control. Figure 6.20 shows ex-

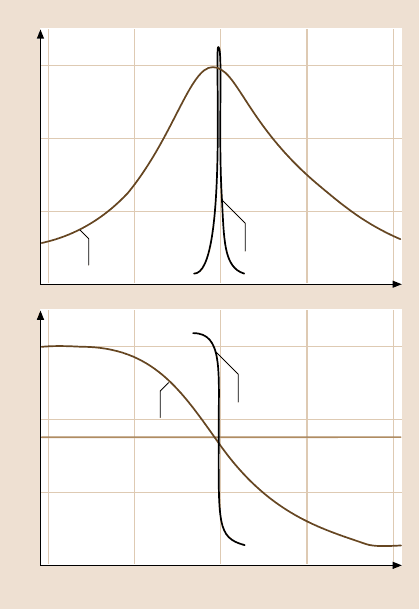
perimental data regarding the eﬀect of Q-control on the amplitude and phase as

a function of the external excitation frequency [51]. In this example, Q-control was

able to increase the Q-value by a factor of over 40.

The eﬀectof improvedimage contrastis demonstratedin Fig. 6.21.Here, a com-

puter hard disk was analyzed with a magnetic tip in tapping mode, where the mag-

netic contrast is observed in the phase image. The upper part shows the recorded

magnetic data structures in standard mode, whereas in the lower part of the image

Q-control feedback was activated, giving rise to an improved signal, i.e., magnetic

contrast. A more detailed analysis of measurements on a magnetic tape shows that

264 A. Schirmeisen et al.

259.5

0.6

0.4

0.2

0.0

Amplitude (arb.units)

180

Frequency (kHz)

Phase (deg)

260.0 260.5 261.5261.0

Q-control off

Q = 499

Q-control on

Q = 19.379

Q-control off

Q = 499

Q-control on

Q = 19.379

Fig. 6.20. Amplitude and

phase diagrams measured

in air with a Si cantilever

far away from the sample.

The quality factor can be in-

creased from 450 to 20,000

by using the Q-control feed-

back method

the signal amplitude (upper diagrams in Fig. 6.22) was increased by a factor of 12.4

by the Q-control feedback. The lower image shows a noise analysis of the signal,

indicating an improvement of the signal-to-noise ratio by a factor of 2.3.

Note that the diagrams represent measurements in air with an AFM operated in

AM mode. Only then can we make a distinction between excitation and vibration

frequency, since in the FM mode these two frequencies are equal by deﬁnition. Al-

though the relation between sensitivity and Q-factor in (6.17) is the same for AM

and FM mode, it must be critically investigated whether the enhanced quality factor

by Q-control can be inserted in the equation for FM-mode AFM. In vacuum appli-

cations, Q is already very high, which makes it unnecessary to operate an additional

Q-control module.

As stated before, we can also use Q-control to enhance the damping in the os-

cillating system. This would decrease the sensitivity of the system. But on the other

hand, the response time of the amplitude change is decreased as well. For tapping-

mode applications, where high-speed scanning is the goal, Q-control was able to

reduce the scan speed that limits relaxation time [52].

6 Dynamic Modes of Atomic Force Microscopy 265

Norm. standard deviation (%)

MFM phase (deg)

X-position (nm)

0 200 400 600 800 1.000 0 200 400 600 800 1.000

MFM phase (deg)

Norm. standard deviation (%)

Q-control off Q-control on

0.25

0 0.25 0.50 0.75 1.00

3.7

46.0

2.1 %

0.9 %

Fig. 6.21. Signal-to-noise analysis with a magnetic tip in tapping mode AFM on a magnetic

tape sample with Q-control

Q-control off

Q-control on

Fig. 6.22. Enhancement of the contrast in the phase

channel due to Q-control on a magnetic hard disk

measured with a magnetic tip in tapping-mode

AFM in air. Scan size 5×5 µm, phase range 10deg

(www.nanoanalytics.com)

266 A. Schirmeisen et al.

A large quality factor Q does not only have the virtue of increasing the force

sensitivity of the instrument. It also has the advantage of increasing the parameter

space of stable AFM operation in AM-mode AFM. Consider the resonance curve

of Fig. 6.5. When approaching the tip towards the surface there are two competing

mechanisms: on one hand, we bring the tip closer to the sample, which results in an

increase in attractive forces (see Fig. 6.2). On the other hand, for the case ω>ω

the resonant frequency of the cantilever is shifted towards smaller values due to

the attractive forces, which causes the amplitude to become smaller. This is the de-

sirable regime, where stable operation of the AFM is possible in the net-attractive

regime. But as explained before, below a certain tip–sample separation d

app

,the

system switches suddenly into the intermittent contact mode, where surface mod-

iﬁcations are more likely due to the onset of strong repulsive forces. The steeper

the amplitude curve the larger the regime of stable, net-attractive AFM operation.

Looking at Fig. 6.20 we ﬁnd thatthe slope of the amplitudecurve is governedby the

quality factor Q. A high Q, therefore, facilitates stable operation of the AM-AFM

in the net-attractive regime.

An example can be found in Fig. 6.23. Here, a surface scan of an ultrathin or-

ganic ﬁlm is acquired in tapping mode under ambient conditions. First, the inner

square is scanned without the Q enhancement, and then a wider surface area was

scanned with Q-control applied. The high quality factor provides a larger parameter

space for operating the AFM in the net-attractive regime, allowing good resolution

of the delicate organic surface structure. Without the Q-control the surface struc-

8.00

6.00

4.00

2.00

0 2.00 4.00 6.00 8.00

25.0 nm

12.5 nm

0.0 nm

μm

Tapping

mode

with active

Q-control

Standard

tapping

mode

Fig. 6.23. Imaging of a delicate organic surface with Q-Control. Sample was a Langmuir–

Blodgett ﬁlm (ethyl-2,3-dihydroxyoctadecanoate) on a mica substrate. The topographical

image clearly shows that the highly sensitive sample surface can only be imaged non-

destructively with active Q-control, whereas the periodic repulsive contact with the probe

in standard operation without Q-control leads to a signiﬁcant modiﬁcation or destruction of

the surface structure (data courtesy of Lifeng Chi and coworkers, University of Münster, Ger-

many)

6 Dynamic Modes of Atomic Force Microscopy 267

tures are deformed and even destroyed due to the strong repulsive tip–sample inter-

actions [53–55]. The Q-control feedback also allowed imaging of DNA structures

without predominantlydepressing the soft material duringimaging. It was then pos-

sible to observe a DNA diameter close to the theoretical value [56].

The same technique has been successfully employed to minimize the interaction

forces during scanning in liquids. This is of special relevance for imaging delicate

biologicalsamples in environmentssuch as water or buﬀer solution. When the AFM

probe is submerged in a liquid medium, the oscillation of the AFM cantilever is

strongly aﬀected by hydrodynamic damping. This typically leads to quality factors

below 10 and, accordingly, to a loss in force sensitivity. However, the Q-control

technique allows one to increase the eﬀective quality factor by about three orders

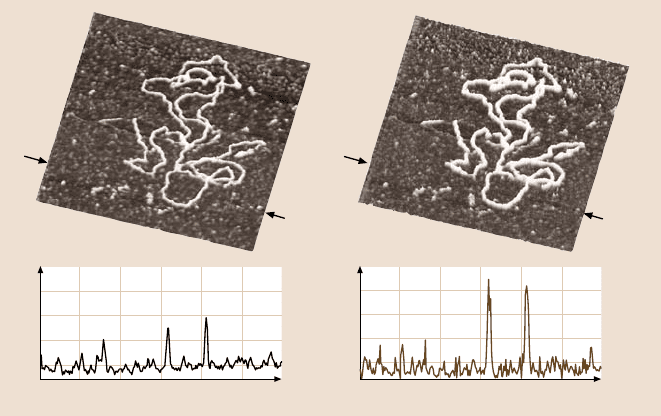
of magnitude in liquids. Figure 6.24 shows results of scanning DNA structures on

a mica substrate under a buﬀer solution. Comparison of the topographic data ob-

tained in standard tapping mode and under Q-Control, in particular the diﬀerence

in the observed DNA height, indicates that the imaging forces were successfully

reduced by employing Q-control.

Height (nm)

x-Position (nm)

600

2.0

1.5

1.0

0.5

500400300200100

Height (nm)

x-Position (nm)

600

2.0

1.5

1.0

0.5

500400300200100

Q-control onQ-control off

Fig. 6.24. AFM images of DNA on mica scanned in buﬀer solution (600 nm×600 nm). Each

scan line was scanned twice: in standard tapping mode during the ﬁrst scan of the line (left

data) and with Q-control activated by a trigger signal during the subsequent scan of the same

line (right data). Thisinterleave technique allows a direct comparison of the resultsof thetwo

modes obtained on the same surface area while minimizing drift eﬀects. Cross sections of the

topographic data reveal that the observed DNA height is signiﬁcantly higher in the case of

imaging under Q-control (data courtesy of Daniel Ebeling and Hendrik Hölscher, University

of Münster, Germany)

268 A. Schirmeisen et al.

In conclusion,we have shown that, by applyingan additional feedbackcircuit to

the dynamic AFM system, it is possible to inﬂuence the quality factor Q of the os-

cillator system. High-resolution, high-speed, or low-force scanning is then possible.

6.5 Dissipation Processes Measured with Dynamic AFM

Dynamic AFM methods have proventheir great potential for imaging surface struc-

tures at the nanoscale, and we have also discussed methods that allow the assess-

ment of forcesbetween distinct singlemolecules.However, thereis another physical

mechanism that can be analyzed with the dynamic mode and has been mentioned in

some previous paragraphs: energy dissipation.

In Fig. 6.12, we have already shown an example, where the phase signal in tap-

ping mode cannot be explained by conservative forces alone; dissipative processes

must also play a role. In constant-amplitude FM mode, where the quantitative in-

terpretation of experiments has proven to be less diﬃcult, an intuitive distinction

between conservative and dissipative tip–sample interaction is possible. We have

shown the correlation between forces and frequency shifts of the oscillating system,

but we have neglected one experimental input channel; the excitation amplitude,

which is necessary to keep the oscillation amplitude constant, is a direct indication

of the energy dissipated during one oscillation cycle. Dürig [57] has shown that

in self-excitation mode (with an excitation–oscillation phase diﬀerence of 90 deg),

conservativeand dissipative interactions can be strictly separated. Part of this energy

is dissipated in the cantilever itself, another part is due to external viscous forces in

the surrounding medium. But more interestingly, some energy is dissipated at the

tip–sample junction. This is the focus of the following paragraphs.

In contrast to conservative forces acting at the tip–sample junction, which

at least in vacuum can be understood in terms of van der Waals, electrostatic,

and chemical interactions, the dissipative processes are poorly understood. Stowe

et al. [58] have shown that, if a voltage potential is applied between tip and sam-

ple, charges are induced in the sample surface, which will follow the tip motion (in

their set-up the oscillation was parallel to the surface). Due to the ﬁnite resistance

of the sample material, energy will be dissipated during the charge movement. This

eﬀect has been exploited to image the doping level of semiconductors. Energy dis-

sipation has also been observedin imaging magnetic materials. Liu et al. [59] found

that energy dissipation due to magnetic interactions was enhanced at the boundaries

of magnetic domains, which was attributed to domain-wall oscillations, and even

a simple system such as two clean metal surfaces which are moved in close prox-

imity can give rise to frictional forces. Stipe et al. [60] have measured the energy

dissipation due to ﬂuctuating electromagnetic ﬁelds between two closely spaced

gold surfaces, which was later interpreted by Volokitin and Persson [61] in terms of

van der Waals friction.

Energy dissipation was also observed, in the absence of external electromag-

netic ﬁelds, when the tip and sample were in close proximity, within 1 nm. Clearly,

mechanical surfacerelaxations must give rise to energy losses. One could model the

6 Dynamic Modes of Atomic Force Microscopy 269

AFM tip as a small hammer,hitting the surface at high frequency, possibly resulting

in phonon excitations. From a continuum mechanics point of view, we assume that

the mechanical relaxation of the surface is not only governed by elastic responses.

Viscoelastic eﬀects of soft surfaces will also render a signiﬁcant contribution to en-

ergy dissipation. The whole area of phase imaging in tapping mode is concerned

with those eﬀects [62–64].

In the atomistic view, the last tip atom can be envisaged as changing position

while experiencing the tip–sample force ﬁeld. A strictly reversible change of po-

sition would not result in a loss of energy. Still, it has been pointed out by Sasaki

et al. [65] that a change in atom position would result in a change in the force inter-

action itself. Therefore, it is possible that the tip atom changes position at diﬀerent

tip–surface distances during approach and retraction, eﬀectively causing an atomic-

scale hysteresis to develop. Hoﬀmann et al. [13] and Hembacher et al. [66] have

measured the short-range energy dissipation for diﬀerent combinations of tip and

surface materials in UHV. For atomic-resolution experiments at low temperatures

on graphite [66] it was found that the energy dissipation is a step-like function.

A similar shape of dissipation curves was found in a theoretical analysis by Kan-

torovich and Trevethan [67], where the energy dissipation was directly associated

with atomic instabilities at the sample surface.

Thedissipation channelhas also beenused to image surfaceswith atomic resolu-

tion [68]. Instead of feeding back the distance on the frequency shift, the excitation

amplitude in FM mode has been used as the control signal. The Si(111)-(7×7) re-

construction was successfully imaged in this mode. The step edges of mono-atomic

NaCl islands on single-crystalline copper have also rendered atomic-resolution con-

trast in the dissipation channel [69]. The dissipation processes discussed so far are

mostly in the conﬁguration in which the tip is oscillated perpendicular to the sur-

face. Friction is usually referred to as the energy loss due to lateral movement of

solid bodies in contact. It is interesting to note in this contextthat Israelachivili [70]

has pointed out a quantitative relationship between lateral and vertical (with respect

to the surface) dissipation. He states that the hysteresis in vertical force–distance

curves should equal the energy loss in lateral friction. An experimental conﬁrma-

tion of this conjecture at the molecular level is still missing.

Physical interpretation of energy dissipation processes at the atomic scale seems

to be a daunting task at this point. Nevertheless, we can ﬁnd a quantitative relation

between the energy loss per oscillation cycle and the experimental parameters in

dynamic AFM, as will be shown in the following section.

InstaticAFMitwasfoundthatpermanentchangesofthesamplesurfacebyinden-

tations cancause a hysteresisbetweenapproachand retraction.The area between the

approachand retraction curvesin a force–distancediagram representsthe lostor dis-

sipatedenergycausedby the irreversiblechangeof thesurfacestructure.In dynamic-

mode AFM, the oscillation parameterssuch as amplitude,frequency,and phase must

containtheinformationaboutthedissipatedenergypercycle.Sofar,wehaveresorted

toatreatmentoftheequationofmotionofthecantilevervibrationinordertoﬁndaquan-

270 A. Schirmeisen et al.

titativecorrelationbetweenforcesandtheexperimentalparameters.Forthedissipation

it is useful to treat the system from thepoint of viewof energyconservation.

Assuming that a dynamic system is in equilibrium, the average energy input

must equal the average energy output or dissipation. Applying this rule to an AFM

running in a dynamic mode means that the average power fed into the cantilever os-

cillation by an external driver, denoted by

, must equal the average power dissi-

pated by the motion of the cantileverbeam

andby thetip–sampleinteraction P

tip

= P

+ P

tip

. (6.29)

The term

tip

is what we are interested in, since it gives us a direct physical quan-

tity to characterize the tip–sample interaction. Therefore, we ﬁrst have to calculate

and then measure the two other terms in (6.29) in order to determine the power

dissipated when the tip periodically probes the sample surface. This requires an

appropriate rheological model to describe the dynamic system. Although there are

investigations in which the complete ﬂexural motion of the cantilever beam has

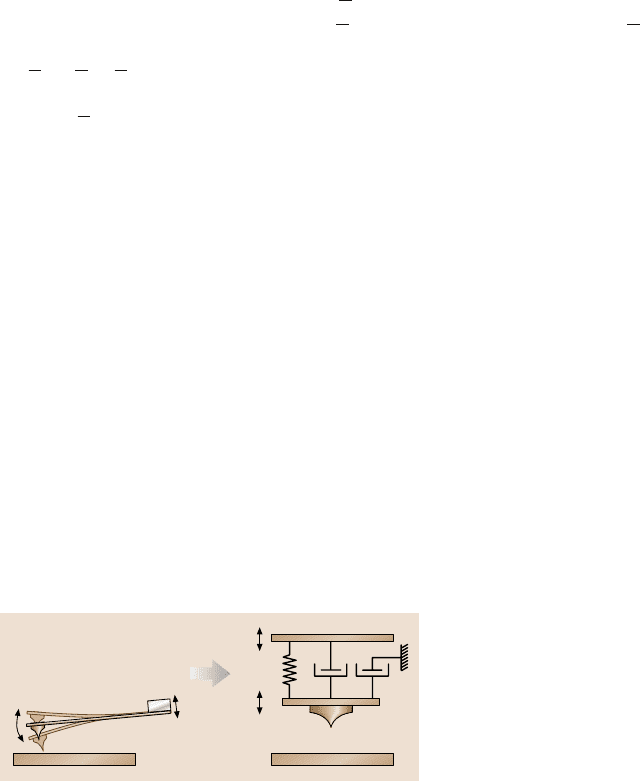
been considered [71], a simpliﬁed model, comprising a spring and two dashpots

(Fig. 6.25), represents a good approximation in this case [72].

The spring, characterized by the constant k according to Hooke’s law, represents

the only channel through which power P

can be delivered to the oscillating tip z(t)

by the external driverz

(t). Therefore,the instantaneouspower fed into the dynamic

system is equal to the force exerted by the driver times the velocity of the driver (the

force that is necessary to move the base side of the dashpot can be neglected, since

this power is directly dissipated and, therefore, does not contribute to the power

delivered to the oscillating tip):

(t) = F

(t)˙z

(t) = k[z(t)−z

(t)]˙z

(t). (6.30)

Assuming a sinusoidal steady-state response and that the base of the cantilever is

driven sinusoidally (see (6.6)) with amplitude A

and frequency ω, the deﬂection

(t)

z(t)

Fig. 6.25. Rheological models applied to describe the dynamic AFM system, comprising

the oscillating cantilever and tip interacting with the sample surface. The movement of the

cantilever base and the tip is denoted by z

(t)andz(t), respectively. The cantilever is char-

acterized by the spring constant k and the damping constant α. In a ﬁrst approach damping

is broken into two pieces α

and α

: ﬁrstly, intrinsic damping caused by the movement of

the cantilever’s tip relative to its base, and secondly, damping related to the movement of the

cantilever body in a surrounding medium, e.g. air damping

6 Dynamic Modes of Atomic Force Microscopy 271

from equilibrium of the end of the cantilever follows (6.9), where A and 0 ≤ ϕ ≤ π

are the oscillation amplitudeand phase shift, respectively. This allowsus to calculate

the average power input per oscillation cycle by integrating (6.30) over one period

T = 2π/ω:



(t)dt =

kωA

Asinϕ. (6.31)

This contains the familiarresultthat the maximum poweris deliveredto an oscillator

when the response is 90deg out of phase with the drive.

The simpliﬁed rheological model, as depicted in Fig. 6.25, exhibits two major

contributions to the damping term

. Both are related to the motion of the can-

tilever body and assumed to be well modeled by viscous damping with coeﬃcients

and α

. The dominant dampingmechanism in UHV conditionsis intrinsic damp-

ing, caused by the deﬂection of the cantilever beam, i.e., the motion of the tip rel-

ative to the cantilever base. Therefore the instantaneous power dissipated by such

a mechanism is given by

(t) = |F

(t)˙z(t)| = |α

[˙z(t)−˙z

(t)]˙z(t)|. (6.32)

Note that the absolute value has to be calculated, since all dissipated power is lost

and, therefore, cannot be returned to the dynamic system.

However, when running an AFM in ambient conditions an additional damping

mechanism has to be considered; damping due to the motion of the cantilever body

in the surrounding medium, e.g., air damping, is in most cases the dominant eﬀect.

The corresponding instantaneous power dissipation is given by

(t) = |F

(t)˙z(t)| = α

˙z

(t). (6.33)

In order to calculate the average power dissipation, (6.32) and (6.33) have to be

integrated over one complete oscillation cycle. This yields



(t)dt

⎡

⎢

⎣

(A−A

cosϕ)arcsin

⎛

⎜

⎝

A−A

cosϕ

−2AA

cosϕ

⎞

⎟

⎠

+ A

sinϕ

⎤

⎥

⎦

(6.34)

and



(t)dt =

. (6.35)

Considering the fact that commonly used cantilevers exhibit a quality factor of at

least several hundreds (in UHV even several ten thousands), we can assume that

the oscillation amplitude is signiﬁcantly larger than the drive amplitude when the

dynamic system is driven at or near its resonance frequency: A  A

. Therefore

(6.34) can be simpliﬁed in a ﬁrst-order approximation to an expression similar to