Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

252 A. Schirmeisen et al.

20 22 24

Amplitude (nm)

Phase (deg)

ω < ω

b) c)

z-position (nm)

135

180

0 10203040

z-position (nm)

0 10203040

z-position (nm)

0 10203040

Amplitude (nm)

Phase (deg)

135

180

Amplitude (nm)

Phase (deg)

135

180

ret

app

ret

app

ret

app

ret

app

ret

app

ret

app

Fig. 6.12. Amplitude and phase diagrams with excitation frequency (a)below(b) exactly

at and (c) above the resonant frequency for tapping-mode AFM from experiments with a Si

cantilever on a Si wafer in air

the resonant frequency towards smaller values, induced by the attractive force in-

teraction, will reduce the oscillation amplitude. The distance between the tip and

sample is, therefore, reduced as well, and the self-amplifying eﬀect with the sudden

instability does not occur as long as repulsive forces are not encountered. However,

at closer tip–sample distances, repulsive forces will cause the resonant frequency

to shift again towards higher values, increasing the amplitude with decreasing tip–

sample distance. Therefore, a self-enhancing instability will also occur in this case,

but at the crossover from purely attractive forces to the regime where repulsive

forces occur. Correspondingly, a small kink in the amplitude curve can be observed

in Fig. 6.11b. An even clearer indication of this eﬀect is manifested by the sudden

change in the phase signal at d

app

In thelast case, with ω>ω

,theeﬀect of amplitudereductiondue tothe resonant

frequency shift is even larger. Again, we ﬁnd no instability in the amplitude signal

during approach in the attractive force regime. However, as soon as the repulsive

force regime is reached, the instability occurs due to the induced positive frequency

shift. Consequently, a large jump in the phase curvefrom valuessmaller than 90 deg

to values larger than 90 deg is observed. The small change in the amplitude curve is

not resolved in the simulated curves in Fig. 6.11c, however, it can be clearly seen in

the experimental curves.

Figure 6.12depicts the correspondingexperimental amplitudeand phase curves.

The measurements were performed in air with a Si cantilever approaching a Si

wafer, with a cantilever resonant frequency of 299.95kHz. Qualitatively, all promi-

nent features of the simulatedcurves can also be found in the experimentaldata sets.

Hence, this model seems to capture the important factors necessary for an appropri-

ate description of the experimental situation.

6 Dynamic Modes of Atomic Force Microscopy 253

But what is the reason for this unexpected behavior? We have to turn to the

numerical simulations again, where we have access to all physical parameters, in

order to understand the underlying processes. The lower part of Fig. 6.11 also

shows the interaction force between the tip and the sample at the point of closest

approach, i.e., the sample-side turnaround point of the oscillation. We see that ex-

actly at the points of the discontinuities the total interaction force changes from the

net-attractive regime to the attractive–repulsive regime, also termed the intermittent

contact regime. The term net-attractive is used to emphasize that the total force is

attractive, despite the fact that some minor contributions might still originate from

repulsive forces. As soon as a minimum distance is reached, the tip also starts to

experience repulsive forces, which completely changes the oscillation behavior. In

other words, the dynamic system switches between two oscillatory states.

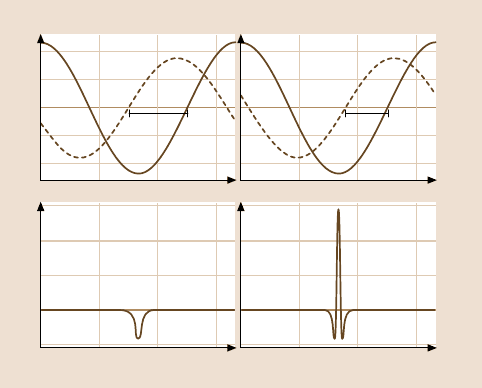
Directly related to this fact is the second phenomenon: the hysteresis eﬀect.

We ﬁnd separate curves for the approach of the probe towards the surface and the

retraction. This seems to be somewhat counterintuitive, since the tip is constantly

approaching and retreating from the surface, and the average values of amplitude

and phase should be independentof the direction of the averagetip–sample distance

movement. A hysteresis between approach and retraction within one oscillation due

to dissipative processes should directly inﬂuence amplitude and phase. However,

no dissipation models were included in the simulation. In this case, the hysteresis in

Fig. 6.11 is due to the fact that the oscillation jumps into diﬀerent modes; the system

exhibits bistability. This eﬀect is often observed in oscillators under the inﬂuence of

nonlinear forces [23].

For the interpretation of these eﬀects it is helpful to look at Fig. 6.13, which

shows the behavior of the simulated tip trajectory and the force during one oscil-

lation cycle over time. The data is shown for the z-positions where hysteresis is

observed, while (a) was taken during the approach and (b) during the retraction.

Excitation was in resonance, where the amplitude shows a small hysteresis. Also

note that the amplitude is almost exactly the same in (a) and (b). We see that the

oscillation at the same z-position exhibits two diﬀerent modes: while in (a) the ex-

perienced force is net-attractive, in (b) the tip is exposed to attractive and repulsive

interactions. Experimentaland simulated datashow that thechange between thenet-

attractive and intermittent contact mode takes place at diﬀerent z-positions (d

app

and

ret

) for approach and retraction. Between d

app

and d

ret

the system is in a bistable

mode. Depending on the history of the measurement, e.g., whether the position d

app

during the approach (or d

ret

during retraction) has been reached, the system ﬂips to

the other oscillation mode. While the amplitude might not be inﬂuenced strongly,

the phase is a clear indicator of the mode switch. On the other hand, if the point

app

is never reached during the approach, the system will stay in the net-attractive

regime and no hysteresis is observed, i.e., the system remains stable.

In conclusion, we ﬁnd that, although a qualitative interpretation of the inter-

action forces is possible, the AM-AFM is not suitable to gain direct quantitative

knowledge of tip–sample force interactions. However, it is a very useful tool for

imaging nanometer-sized structures in a wide variety of setups, in air or even in

254 A. Schirmeisen et al.

Deflection (nm)

Force (nN)

a) b)

Time (μs)

–10

–20

–10

Time (μs)

Excitation (Å)

1.0

0.5

0.0

– 0.5

– 1.0

01230123

Repulsive

Attractive

Repulsive

Attractive

Fig. 6.13. Simulation of the tapping-mode cantilever oscillation in the (a) net-attractive and

(b) the intermittent contact regime. The dashed line represents the excitation amplitude and

the solid line is the oscillation amplitude

liquid. We ﬁnd that two distinct modes exist for the externally excited oscillation –

the net-attractive and the intermittent contact mode – which describe what kind of

forces govern the tip–sample interaction. The phase can be used as an indicator of

the current mode of the system.

In particular, it can be easily seen that, if the free resonant frequency of the can-

tilever is higher than the excitation frequency, the system cannot stay in the net-

attractive regime due to a self-enhancing instability. Since in many applications

involving soft and delicate biological samples strong repulsive forces should be

avoided,the tapping-modeAFM shouldbe operatedat frequenciesequal to or above

the free resonant frequency [24]. Even then, statistical changes of tip–sample forces

during the scan might induce a sudden jump into the intermittent contact mode, and

the previously explained hysteresis will tend to keep the system in this mode. It is

therefore of high importance to tune the oscillation parameters in such a way that

the AFM stays in the net-attractive regime [25]. A concept that achieves this task

is the Q-control system, which will be discussed in some detail in the forthcoming

paragraphs.

A last word concerning the overlap of simulation and experimental data: while

the qualitative agreement down to the detailed shape of hysteresis and instabilities

is rather striking, we still ﬁnd some quantitative discrepancies between the positions

of the instabilities d

app

and d

ret

. This is probably due to the simpliﬁed force model,

which only takes into account van der Waals and repulsive forces. Especially at

ambient conditions, an omnipresent water meniscus between the tip and sample

will give rise to much stronger attractive and also dissipative forces than considered

6 Dynamic Modes of Atomic Force Microscopy 255

Phase (deg)

z-position

180

Δφ

Repulsive

Attractive

Free

Δφ

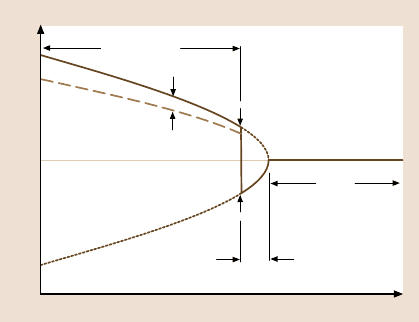
Fig. 6.14. Phase shift in

tapping mode as a function of

tip–sample distance

in the model. A very interesting feature is that the simulated phase curves in the

intermittent contact regime tend to have a steeper slope in the simulation than in the

experiments (seealso Fig. 6.14). We will later show that this eﬀect is a ﬁngerprint of

an eﬀect that was not included in this simulation at all: dissipative processes during

the oscillation, giving rise to an additional loss of oscillation energy.

6.3.2 Self-Excitation Modes

Despite the wide rangeof technical applications of the AM mode of dynamic AFM,

it has been found unsuitable for measurements in an environment extremely useful

for scientiﬁc research: vacuum or ultrahigh vacuum (UHV) with pressures reaching

1×10

−10

mbar. The STM has already shown how much insight can be gained from

some highly deﬁned experiments under those conditions.

Consider(6.11) from the previoussection. The time constantτ for the amplitude

to adjust to a diﬀerent tip–sample force scales with 1/Q. In vacuum applications, Q

of the cantilever is on the order of 10,000, which means that τ is in the range of

some 10ms. This is clearly too long for a scan of at least (100×100) data points.

On the other hand, the resonant frequency of the system will react instantaneously

to tip–sample forces. This has led Albrecht et al. [11] to use a modiﬁed excitation

scheme.

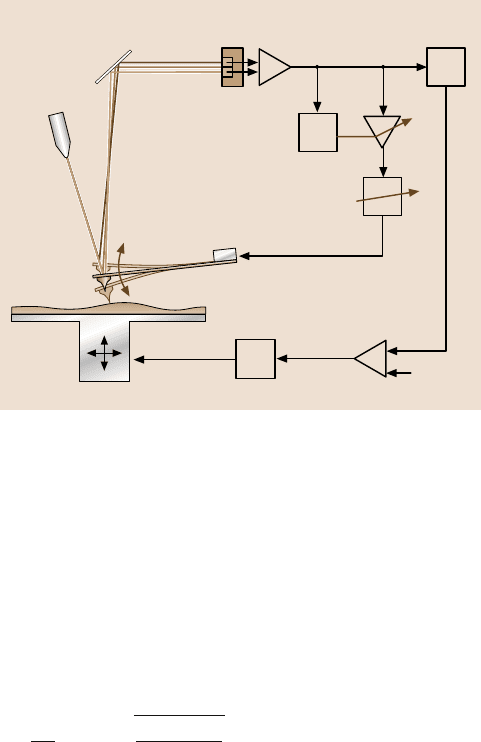
The system is always oscillated at its resonant frequency. This is achieved by

feeding back the oscillation signal from the cantilever into the excitation piezo-

element. Figure 6.15 illustrates the method in a block diagram. The signal from the

PSD is phase-shifted by 90deg (and, therefore, always exciting in resonance) and

used as the excitation signal of the cantilever. An additional feedback loop adjusts

the excitation amplitude in such a way that the oscillation amplitude remains con-

stant. This ensures that the tip–sample distance is not inﬂuenced by changes in the

oscillation amplitude. The only degree of freedom that the oscillation system still

has, which can react to the tip–sample forces, is the change of the resonant fre-

quency. This shift of the frequency is detected and used as the set-point signal for

256 A. Schirmeisen et al.

Laser

Detector

Mirror

Frequency

demodulator

PID-controller

x,y,z-scanner

Piezo

Sample

Cantilever

+ tip

Detector signal

Excitation signal

Set-point

Error signalz-Signal

Amplitude

control

Variable

phase shifter

Fig. 6.15. Dynamic AFM operated in the self-excitation mode, where the oscillation signal is

directlyfed back to theexcitation piezo. The detector signal is ampliﬁedwith thevariable gain

G and phase shifted by phase ϕ. The frequency demodulator detects the frequency shift due

to tip–sample interactions, which serves as the control signal for the probe–sample distance

surface scans. Therefore, this mode is also called the frequency-modulated (FM)

mode.

Let us take a look at the sensitivity of the dynamic AFM. If electronic noise,

lasernoise,and thermaldriftcan be neglected,the main noisecontributionwill come

from thermal excitations of the cantilever. A detailed analysis of a dynamic system

yields, for the minimum detectable force gradient, the following relation [11]:

∂F

∂z

MIN



4k·k

T ·B



osc



(6.17)

Here B is the bandwidth of the measurement, T the temperature, and



osc



is the

mean-square amplitude of the oscillation. Please note that this sensitivity limit was

deliberately calculated for the FM mode. A similar analysis of the AM mode, how-

ever, yields virtually the same result [26].We ﬁnd that the minimum detectable force

gradient, i.e., the measurement sensitivity, is inversely proportional to the square

rootof the Q-factor of the cantilever. This meansthat it should bepossible to achieve

very high-resolution imaging under vacuum conditions where the Q-factor is very

high.

A breakthrough in high-resolution AFM imaging was the atomic-resolution

imaging of the Si(111)–(7×7) surface reconstruction by Giessibl [8] under UHV

conditions. Moreover, Sugawara et al. [27] observed the motion of single atomic

defects on InP with true atomic resolution. However, imaging on conducting or

6 Dynamic Modes of Atomic Force Microscopy 257

semiconducting surfaces is also possible with the scanning tunneling microscope

(STM) and these ﬁrst non-contact AFM (NC-AFM) images provided little new in-

formation on surface properties. The true potential of NC-AFM lies in the imag-

ing of nonconducting surface with atomic precision, which was ﬁrst demonstrated

by Bammerlin et al. [28] on NaCl. A long-standing question about the surface re-

construction of the technologically relevant material aluminium oxide could be an-

sweredby Barthet al. [29],whoimagedthe atomic structureof thehigh-temperature

phase of α-Al

(0001).

The high-resolution capabilities of non-contact atomic force microscopy are

nicely demonstrated by the images shown in Fig. 6.16. Allers et al. [30] imaged

steps and defects on the insulator nickel oxide with atomic resolution. Such a reso-

Fig. 6.16. Imaging of a NiO(001) sample surface with non-contact AFM. (a) Surface step

and an atomic defect. The lateral distance between two atoms is 4.17 Å. (b) A dopant atom is

imaged as a light protrusion about 0.1 Å higher than the other atoms. (Images courtesy of W.

Allers and S. Langkat, University of Hamburg)

258 A. Schirmeisen et al.

lution is routinely obtained today by diﬀerent research groups (for an overview see,

e.g., [31–33]).

However, we are concerned with measuring atomic force potentials of a single

pair of molecules. Clearly, FM-mode AFM will allow us to identify single atoms,

and with suﬃcient care we will be able to ensure that only one atom from the tip

contributes to the total force interaction. Can we, therefore, ﬁll in the last bit of

information and ﬁnd a quantitative relation between the oscillation parameters and

the force?

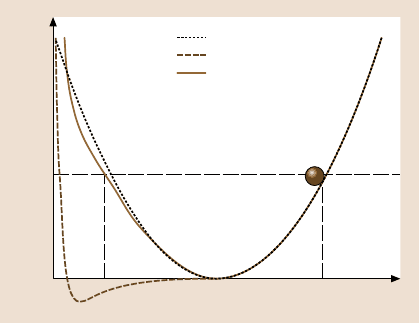
A good insight into the cantilever dynamics can be drawn from the tip potential

displayed in Fig. 6.17 [34]. If the cantilever is far away from the sample surface,

the tip moves in a symmetric parabolic potential (dotted line), and the oscillation is

harmonic. In such a case, the tip motion is sinusoidal and the resonant frequency is

determined by the eigenfrequency f

of the cantilever. If the cantilever approaches

the samplesurfacethe potentialis changed, given byan eﬀectivepotential V

eﬀ

(solid

line) which is the sum of the parabolic potential and the tip–sample interaction po-

tential V

(dashed line). This eﬀective potential diﬀers from the original parabolic

potential and shows an asymmetric shape. As a result the oscillation becomes an-

harmonic, and the resonant frequency of the cantilever depends on the oscillation

amplitude.

Gotsmann et al. [35] investigated this relation with a numerical simulation. Dur-

ing each oscillation cycle the tip experiences a whole range of forces. For each step

during the approach the diﬀerential equation for the whole oscillation loop (also

including the feedback system) was evaluated and ﬁnally the quantitative relation

between the force and frequency shift was revealed.

However, there is also an analytical relationship, if some approximations are

accepted [7,36,37]. Here, we will follow the route indicated by [37], although alter-

native ways have also been proven successful. Consider the tip oscillation trajectory

reaches over a large part of the force gradient curve in Fig. 6.2. We model the tip–

sample interaction as a spring constant of stiﬀness k

(z) = ∂F/∂z|

as in Fig. 6.1.

Cantilever potential

Tip-sample potential

Effective potential

min

D + 2Az

V(z)

Fig. 6.17. The frequency shift

in dynamic force microscopy

is caused by the tip–sample

interaction potential (dashed

line), which alters the har-

monic cantilever potential

(dotted line). Therefore, the

tip moves in an anharmonic

and asymmetric eﬀective po-

tential (solid line). Here, z

min

is the minimum position of

the eﬀective potential (from

Hölscher et al. [34])

6 Dynamic Modes of Atomic Force Microscopy 259

For small oscillation amplitudes we already found that the frequency shift is pro-

portional to the force gradient in (6.4). For large amplitudes, we can calculate an

eﬀective force gradient k

eﬀ

as a convolution of the force and the fraction of time, the

tip spends between the positions x and x+ dx:

eﬀ

(z) =

πA



z+2A

F(x)·g



x−z

−1



dx with g(u) = −

√

1−u

. (6.18)

In the approximation that the vibration amplitude is much larger than the range of

the tip sample forces the above equation can be simpliﬁed to:

eﬀ

(z) =

√

3/2



∞

F(x)

√

x−z

dx. (6.19)

This eﬀective force gradient can now be used in (6.4), the relation between the

frequency shift and force gradient. We ﬁnd:

Δ f =

√

2π ·kA

3/2



∞

F(x)

√

x−z

dx. (6.20)

If we separate the integral from other parameters, we can deﬁne:

Δ f =

3/2

·γ(z)

with γ(z) =

√

2π



∞

F(x)

√

x−z

dx. (6.21)

This means we can deﬁne γ(z), which is only dependent on the shape of the force

curve F(z) but independent of the external parameters of the oscillation. The func-

tion γ(z)isalsoreferredtoasthenormalized frequency shift [7], a very useful pa-

rameter, which allows us to compare measurements independent of resonant fre-

quency, amplitude and spring constant of the cantilever.

The dependence of the frequency shift on the vibration amplitude is an espe-

cially useful relation, since this parameter can be easily varied during one exper-

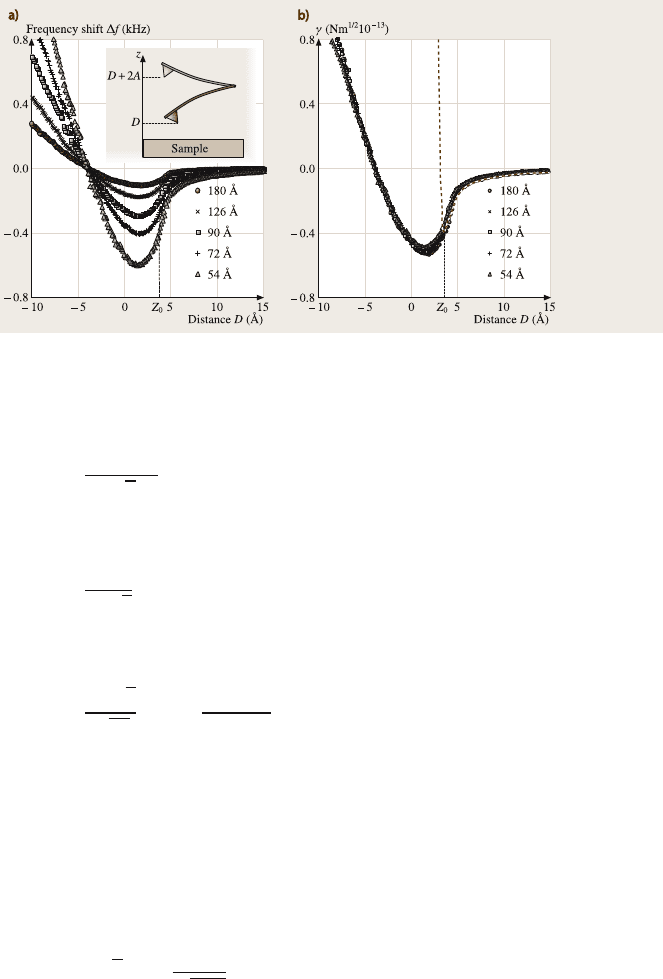
iment. A nice example is depicted in Fig. 6.18, where frequency shift curves for

diﬀerent amplitudes were found to coincide very well in the γ(z) diagrams [38].

This relationship has been nicely exploited for the calibration of the vibration

amplitude by Guggisberg [39], which is a problem often encountered in dynamic

AFM operation and worthwhile discussing. One approaches tip and sample and

records frequency shift versus distance curves, which show a reproducible shape.

Then, with the z-feedback disabled, several curves with diﬀerent amplitudes are

acquired. The amplitudes are typically chosen by adjusting the amplitude set point

in volts. One has to take care that drift in the z-direction is negligible. An analysis

of the correspondingγ(z)-curves will show the same curves (as in Fig. 6.18), but the

curves will be shifted in the horizontal axis. These shifts correspond to the change

in amplitude, allowing one to correlate the voltage values with the z-distances.

For the often-encounteredforce contributionsfrom electrostatic, van der Waals,

and chemical binding forces the frequency shift has been calculated from the force

laws. In the approximation that the tip radius R is larger than the tip–sample dis-

tance z, an electrostatic potential V will yield a normalized frequency shift of

(adapted from Guggisberg [40]):

260 A. Schirmeisen et al.

Fig. 6.18. (a) Frequency shift curves for diﬀerent oscillation amplitudes for a silicon tip on

a graphite surface in UHV, (b) γ-curves calculated from the Δ f-curves in (a) (reprinted from

Hölscher et al. [38] with permission, Copyright (2000) by The American Physical Society)

γ(z) =

πε

R·V

√

·z

−1/2

. (6.22)

For van der Waals forces with Hamaker constant H and also with R larger than z we

ﬁnd accordingly:

γ(z) =

H·R

√

·z

−3/2

(6.23)

Finally, short-range chemical forces represented by the Morse potential (with the

parameters binding energy U

, decay length λ and equilibrium distance z

equ

yield:

γ(z) =

√

πλ

·exp



−

(z−z

equ

)



. (6.24)

These equations allow the experimentalist to interpret the spectroscopic measure-

ments directly. For example, the contributions of the electrostatic and van der Waals

forces can be easily distinguished by their slope in a double logarithmic plot (for an

example, see Guggisberg et al. [40]).

Alternatively, if the force law is not known beforehand, the experimentalist

wants to analyze the experimental frequency-shift data curves and extract the force

or energy potential curves. We, therefore, have to invert the integral in (6.21) to ﬁnd

the tip–sample interaction potential V

from the γ(z)-curves [37]:

(z) =

√

2·



∞

γ(x)

√

x−z

dx. (6.25)

Using this method, quantitative force curves were extracted from Δ f-spectroscopy

measurements on diﬀerent, atomically resolved sites of the Si(111)-(7×7) recon-

struction [1]. Comparison to theoretical molecular dynamics (MD) simulations

6 Dynamic Modes of Atomic Force Microscopy 261

showed good quantitative agreement with theory and conﬁrmed the assumption

that force interactions were governed by a single atom at the tip apex. Our initially

formulated goal seems to be achieved: with FM-AFM we have found a powerful

method that allows us to measure the chemical bond formation of single molecules.

The last uncertainty, the exact shape and identity of the tip apex atom, can possi-

bly be resolved by employing the FIM technique to characterize the tip surface in

combination with FM-AFM.

All the above equations are only valid in the approximation that the oscilla-

tion amplitudes are much larger than the distance range of the encountered forces.

However, for amplitudes of, e.g., 10 nm and long-ranged forces like electrostatic

interactions this approximation is no longer valid. Several approaches have been

proposed by diﬀerent authors to solve this issue [41–43]. The matrix method [42]

uses the fact that in a real experiment the frequency shift curve is not continuous,

but rather a set of discrete values acquired at equidistant points. Therefore the in-

tegral in (6.18) can be substituted by a sum and the equation can be rewritten as

a linear equation system, which in turn can be easily inverted by appropriate matrix

operations. This matrix method is a very simple and general method for the AFM

user to extract force curves from experimental frequency-shift curves without the

restrictions of the large-amplitude approximation.

In this context it is worthwhile to point out a slightly diﬀerent dynamic AFM

method. While in the typical FM-AFM set-up the oscillation amplitude is controlled

to stay constant by a dedicated feedback circuit, one could simply keep the excita-

tion amplitude constant (this has been termed the constant-excitation (CE) mode as

opposed to the constant-amplitude (CA) mode. It is expected that this mode is more

gentle to the surface, because any dissipative interaction will reduce the amplitude

and therefore prevent a further reduction of the eﬀective tip–sample distance. This

mode has been employed to image soft biological molecules like DNA or thiols in

UHV [44].

At ﬁrst glance, quantitative interpretation of the obtained frequency spectra

seems more complicated, since the amplitude as well as the tip–sample distance is

altered during the measurement. However, it was found by Hölscher et al. [45] that

for the CE mode in the large-amplitude approximation the distance and the ampli-

tude channel can be decoupledby calculating the eﬀective tip–sampledistance from

the piezo-controlled tip–sample distance z and the change in the amplitude with dis-

tance A(z):z

eﬀ

(z) = z−A(z). As a result, (6.21) can then be directly used to calculate

the normalized frequency shift γ(z

eﬀ

) and consequently the force curve can be ob-

tained from (6.25). This concept has been veriﬁed in experiments by Schirmeisen

et al. [46] through a direct comparison of spectroscopy curves acquired in the CE

and CA modes.

Until now, we have always associated the self-excitation scheme with vacuum

applications. Although it is diﬃcult to operate FM-AFM in constant-amplitude

mode in air, since large dissipative eﬀects make it diﬃcult to ensure a constant

amplitude, it is indeed possible to use constant-excitation FM-AFM in air or even

in liquids. However, only a few applications of FM-AFM under ambient or liquid