Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

242 A. Schirmeisen et al.

of the cantilever for lateral friction measurements). With the cantilever in equilib-

rium, the spot is adjusted such that the two sections show the same intensity. If the

cantilever bends up or down, the spot moves, and the diﬀerence signal between the

upper and lower sections is a measure of the bending.

In order to enhance sensitivity, several groups have adopted an interferometer

system to measure the cantilever deﬂection. A thorough comparison of diﬀerent

measurement methods with analysis of sensitivity and noise level is given in refer-

ence [3].

The cantilever is mounted on a device that allows oscillation of the beam. Typ-

ically a piezo-element directly underneath the cantilever beam serves this purpose.

The reﬂected laser beam is analyzed for oscillation amplitude, frequency and phase

diﬀerence. Depending on the mode of operation, a feedback mechanism will ad-

just the oscillation parameters and/or tip–sample distance during the scanning. The

set-up can be operated in air, UHV, and even in ﬂuids. This allows measurement of

a wide range of surface properties from atomic-resolution imaging [8] up to study-

ing biological processes in liquids [9,10].

6.2 Harmonic Oscillator: A Model System for Dynamic AFM

The oscillating cantilever has three degrees of freedom: the amplitude, the fre-

quency, and the phase diﬀerence between excitation and oscillation. Let us consider

the dampeddriven harmonic oscillator. The cantilever is mounted on a piezoelectric

element that is oscillating with amplitude A

at frequency ω:

(t) = A

cos(ωt). (6.6)

We assume that the cantilever spring obeys Hooke’s law. Secondly, we introduce

a friction force that is proportional to the speed of the cantilever motion, with α

denoting the damping coeﬃcient (Amontons’s law). With Newton’s ﬁrst law we

ﬁnd for the oscillating system the following equation of motion for the position z(t)

of the cantilever tip (see also Fig. 6.1):

m¨z(t) = −α˙z(t)−kz(t)−kz

(t); (6.7)

We deﬁne ω

= k/m

∗

, which turns out to be the resonant frequency of the free (un-

damped, i.e., α = 0) oscillating beam. We further deﬁne the dimensionless quality

factor Q= m

∗

/α, whichisantiproportionalto thedampingcoeﬃcient. The quality

factor describes the number of oscillation cycles after which the damped oscillation

amplitude decays to 1/e of the initial amplitude with no external excitation (A

= 0).

After some basic manipulation, this results in the following diﬀerential equation:

¨z(t)+

˙z(t)+ ω

z(t) = A

cos(ωt). (6.8)

The solution is a linear combination of two regimes [11]. Starting from rest and

switching on the piezo-excitation at t = 0, the amplitude will increase from zero to

6 Dynamic Modes of Atomic Force Microscopy 243

the ﬁnal magnitude and reach a steady state, where the amplitude, phase, and fre-

quency of the oscillation stay constant over time. The steady-state solution z

(t)is

reached after 2Q oscillation cycles and follows the external excitation with ampli-

tude A

and phase diﬀerence ϕ:

(t) = A

cos(ωt+ ϕ) (6.9)

The oscillation amplitude in the transient regime during the ﬁrst 2Q cycles follows:

(t) = A

· e

−ω

t/2Q

·sin(ω

t+ ϕ

). (6.10)

We emphasize the important fact that the exponential term causes z

(t) to diminish

exponentially with time constant τ:

τ = 2Q/ω

(6.11)

In vacuum conditions, only the internal dissipation due to bending of the can-

tilever is present, and Q reaches values of 10,000 at typical resonant frequencies

of 100,000Hz. This results in a relatively long transient regime of τ  30ms, which

limits the possible operational modes for dynamic AFM (detailed analysis by [11]).

Changes in the measured amplitude, which reﬂect a change of atomic forces, will

have a time lag of 30ms, which is very slow considering one wants to scan a 200 ×

200point image within a few minutes. In air, however, viscous damping due to air

friction dominates and Q goes down to less than 1000, resulting in a time constant

below the millisecond level. This response time is fast enough to use the amplitude

as a measurement parameter.

If we evaluate the steady-state solution z

(t) of the diﬀerential equation, we ﬁnd

the following well-known solution for amplitude and phase of the oscillation as

a function of the excitation frequency ω:

·Q·ω

+ Q



−ω



(6.12)

ϕ = arctan

⎛

⎜

⎝

ω ·ω

Q·



−ω



⎞

⎟

⎠

. (6.13)

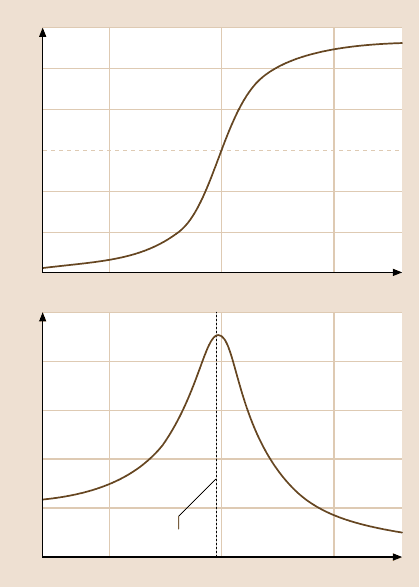
Amplitude and phase diagrams are depicted in Fig. 6.5. As can be seen from (6.12)

the amplitude will reach its maximum at a frequency diﬀerent from ω

,ifQ has

a ﬁnite value. The damping term of the harmonic oscillator causes the resonant

frequency to shift from ω

to ω

∗

= ω



1−

(6.14)

The shift is negligible for Q-factors of 100 and above,which is the case for most ap-

plications in vacuum or air. However, for measurements in liquids, Q can be smaller

244 A. Schirmeisen et al.

0.5 1.0 1.5

180

150

120

1.0

0.8

0.6

0.4

0.2

0.0

Phase (deg)

Amplitude (arb. units)

ω/ω

ω*

/ω

0.5 1.0 1.5

Fig. 6.5. Curves of amplitude

and phase versus excitation

frequency for the damped

harmonic oscillator, with

a quality factor of Q = 4

than 10 and ω

diﬀers signiﬁcantly from ω

∗

. As we will discuss later, it is also

possible to enhance Q by using a special excitation method called Q-control.

In the case that the excitationfrequency is equal to the resonant frequencyof the

undamped cantilever ω = ω

, we ﬁnd the useful relation:

= Q·A

for ω = ω

. (6.15)

Since ω

∗

≈ ω

for most cases, we ﬁnd that (6.15) holds true when exciting the can-

tilever at its resonance. From a similar argument, the phase becomes approximately

90deg for the resonance case. We also see that, in order to reach vibration ampli-

tudes of some 10nm, the excitation can be as small as 1 pm for typical cantilevers

operated in vacuum.

So far, we have not considered an additional force term that describes the in-

teraction between the probing tip and the sample. For typical large-vibration ampli-

tudes of 10–100nm no general solution for this analytical problem has been found

yet. The cantilevertip will experience a whole range of force interactions during one

single oscillation cycle, rather than one deﬁned tip–sample force. Only in thespecial

case of a self-excited cantilever oscillation can the problem be solved analytically,

as we will see later.

6 Dynamic Modes of Atomic Force Microscopy 245

6.3 Dynamic AFM Operational Modes

While the quantitative interpretation of force curves in contact AFM is straightfor-

ward using (6.1), we explained in the previous paragraphs that its application to

assess short-range attractiveinteratomic forces is rather limited. The dynamic mode

of operation seems to open a viable direction towards achieving this task. However

interpretation of the measurements generally appears to be more diﬃcult. Diﬀerent

operational modes are employed in dynamic AFM, and the following paragraphs

are intended to distinguish these modes and categorize them in a systematic way.

The oscillation trajectory of a dynamically driven cantilever is determined by

three parameters: the amplitude, the phase, and the frequency. Tip–sample inter-

actions can inﬂuence all three parameters, which are termed the internal parameters

in the following. The oscillation is driven externally, with excitation amplitude A

andexcitationfrequencyω. Thesevariableswill bereferredto as theexternalparam-

eters. The external parameters are set by the experimentalist, whereas the internal

parameters are measured and contain the crucial information about the force inter-

action. In scanning probe applications, it is common to control the probe–surface

distance z

in order to keep an internal parameter constant (i.e., the tunneling cur-

rent in STM or the beam deﬂection in contact AFM), which represents a certain

tip–sample interaction. In z-spectroscopy mode, the distance is varied in a certain

range, and the change of the internal parameters is measured as a ﬁngerprint of the

tip–sample interactions.

In dynamic AFM the situation is rather complex. Any of the internal parame-

ters can be used for feedback of the tip–sample distance z

. However, we already

realized that, in general, the tip–sample forces can only be fully assessed by meas-

uringall three parameters.Therefore,dynamicAFM imagesare diﬃcultto interpret.

A solution to this problem is to establish additional feedback loops, which keep the

internal parameters constant by adjusting the external variables. In the simplest set-

up, the excitation frequency is set to a predeﬁned value, and the excitation ampli-

tude remains constant by a feedback loop. This is called the amplitude-modulation

(AM) or tapping mode. As stated before, in principle, any of the internal parameters

can be used for feedback to the tip–sample distance; in AM mode the amplitude

signal is used. A certain amplitude (smaller than the free oscillation amplitude) at

a frequency close to the resonance of the cantilever is chosen; the tip is approached

towards the surface under investigation, and the approach is stopped as soon as the

set-point amplitude is reached. The oscillation phase is usually recorded during the

scan, however, the shift of the resonant frequency of the cantilever cannot be di-

rectly accessed, since this degree of freedom is blocked by the external excitation at

a ﬁxed frequency. It turns out that this mode is simple to operate from a technical

perspective,but quantitativeinformation about the tip–sample interaction forces has

so far not been reliably extracted from AM-mode AFM. Despite this, it is one of the

most commonly used modes in dynamic AFM operated in air, and even in liquid.

The strength of this mode is the qualitative imaging of a large variety of surfaces.

It is interesting to discuss the AM mode in the situation that the external exci-

tation frequency is much lower than the resonant frequency [12, 13]. This results

246 A. Schirmeisen et al.

in a quasistatic measurement, although a dynamic oscillation force is applied, and,

therefore, this mode can be viewed as a hybrid between static and dynamic AFM.

Unfortunately, it has the drawbacks of the static mode, namely, that stiﬀ spring con-

stants must be used and, therefore, the sensitivity of the deﬂection measurement

must be very good, typically employing a high-resolution interferometer. However,

it has the advantage of the static measurement in quantitative interpretation, since in

the regime of small amplitudes (< 0.1nm) a direct interpretation of the experiments

is possible. In particular, the force gradient at the tip–sample distance z

is given by

the change of the amplitude A and the phase angle ϕ

∂F

∂z

= k



1−

cosϕ



. (6.16)

In eﬀect, the modulated AFM technique can proﬁt from enhanced sensitivity due to

the use of lock-in techniques, which allow the measurement of the amplitude and

phase of the oscillation signal with high precision.

As stated before, the internal parameters can be fed back to the external exci-

tation variables. One of the most useful applications in this direction is the self-

excitation system. Here the resonant frequency of the cantilever is detected and se-

lected again as the excitation frequency. In a typical set-up, this is done with a phase

shift of 90deg by feeding back the detector signal to the excitation piezo, i.e., the

cantilever is always excited in resonance. Tip–sample interaction forces then only

inﬂuence the resonant frequency, but do not change the two other parameters of the

oscillation: amplitude and phase. Therefore, it is suﬃcient to measure the frequency

shift inducedby the tip–sampleinteraction. Sincethe phase remains at a ﬁxed value,

the oscillating system is much betterdeﬁned than before, and the degreesof freedom

for the oscillation are reduced. To reduce the last degree of freedom even further an

additional feedback loop can be incorporated to keep the oscillation amplitude A

constant by varying the excitation amplitude A

. Now, all internal parameters have

a ﬁxed relation to the external excitation variables, the system is well deﬁned, and

all parameters can be assessed during the measurement. As it turns out, this mode

is the only dynamic mode in which a quantitative relation between the tip–sample

forces and the change of the resonant frequency can be established.

In the following section we want to discuss the two most popular operational

modes, the tapping mode and the self-excitation mode, in more detail.

6.3.1 Amplitude-Modulation/Tapping-Mode AFM

In the tapping mode, or AM-AFM, the cantilever is excited externally at a constant

frequency close to its resonance. The oscillation amplitude and phase during the

approach of the tip and the sample serve as the experimental observation channels.

Figure 6.6 shows a diagram of a typical tapping-mode AFM set-up. The oscillation

of the cantilever is detected with the photodiode, whose output signal is analyzed

with a lock-in ampliﬁer to obtain amplitudeand phase information. The amplitude is

then compared to the set point, and the resulting diﬀerence or error signal is fed into

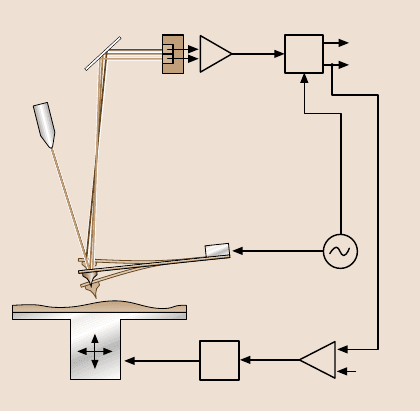
6 Dynamic Modes of Atomic Force Microscopy 247

Laser

Detector

Mirror

Lock-in amplifier

Function

generator

PID-controller

x,y,z-scanner

Piezo

Sample

Cantilever

+ tip

Detector

signal

Phase

Amplitude

Reference

signal

Excitation

signal

Set-point

Error

signal

z-Signal

Fig. 6.6. Set-up of a dynamic

force microscope operated

in the AM or tapping mode.

A laser beam is deﬂected by

the backside of the cantilever

and the deﬂection is detected

by a split photodiode. The ex-

citation frequency is chosen

externally with a modulation

unit, which drives the excita-

tion piezo. A lock-in ampli-

ﬁer analyses the phase and

amplitude of the cantilever

oscillation. The amplitude is

used as the feedback signal

for the probe–sample dis-

tance control

the proportional–integral–derivative(PID)controller,whichadjusts thez-piezo, i.e.,

the probe–sample distance, accordingly. The external modulation unit supplies the

signal for the excitation piezo, and, at the same time, the oscillation signal serves as

the reference for the lock-in ampliﬁer. As shown by the following applications the

tapping mode is typically used to measure surface topography and other material

parameters on the nanometer scale. The tapping mode is mostly used in ambient

conditions and in liquids.

High-resolution imaging has been extensively performed in the area of material

science. Due to its technical relevance the investigation of polymers has been the

focus of many studies (see e.g. a recent review about AFM imaging of polymers

in [15]. In Fig. 6.7 the topography of a diblock copolymer (BC

0.26

-3A

0.53

F8H10) at

diﬀerent magniﬁcationsis shown[14]. On the large scan (a) the large-scalestructure

of the microphase-separated polystyrene (PS) cylinders [within a polyisoprene (PI)

matrix] lying parallel to the substrate can be seen. In the high-resolution image (b)

a surface substructure of regular domes can be seen, which were found to be related

to the cooling process during the polymer preparation.

Imaging in liquids opens up the avenue for the investigation of biological sam-

ples in their naturalenvironment.For example Möller et al. [16] have obtainedhigh-

resolutionimages of the topographyof hexagonallypacked intermediate(HPI) layer

of Deinococcus Radiodurans with tapping-mode AFM. Another interesting exam-

ple is the imaging of deoxyribonucleic acid (DNA) in liquid, as shown in Fig. 6.8.

Jiao et al. [10] measured the time evolution of a single DNA strand interacting with

a molecule, as shown by a sequence of images acquired in liquid over a time period

of several minutes.

For a quantitative interpretation of tip–sample forces one has to consider that

during one oscillation cycle with amplitudes of 10–100nm the tip–sample inter-

248 A. Schirmeisen et al.

1.50

1.00

0.50

500

250

0 0.50 1.00 1.50

μm

0 250 500

μm

Fig. 6.7. Tapping-mode images of BC

0.26

-3A

0.53

F8H10 at (a) low resolution and (b)high

resolution. The height scale is 10 nm. (Reprinted inpart with permission from [14]. Copyright

(2001) American Chemical Society)

4'16''

c) d)

6'13''

12'49'' 14'22''

Fig. 6.8a–d. Dynamic p53-DNA interactions observed by time-lapse tapping-mode AFM

imaging in solution. Both p53 protein and DNA were weakly adsorbed to a mica surface by

balancing the buﬀer conditions. (a) A p53 protein molecule (arrow) was bound to a DNA

fragment. The protein (b) dissociated from and then (c) re-associated with the DNA frag-

ment. (d) A downward movement of the DNA with respect the protein occurred, constituting

a sliding event whereby the protein changes its position on the DNA. Image size: 620 nm.

Colorscale (height) range: 4 nm. Time units: minutes, seconds. (Image courtesy of Tilman

Schäﬀer, University of Münster)

6 Dynamic Modes of Atomic Force Microscopy 249

action will range over a wide distribution of forces, including attractive as well as

repulsive forces. We will, therefore, measure a convolution of the force–distance

curve with the oscillation trajectory. This complicates the interpretation of AM-

AFM measurements appreciably.

At the same time, the resonant frequency of the cantilever will change due to

the appearing force gradients, as could already be seen in the simpliﬁed model from

(6.4). If the cantilever is excited exactly at its resonant frequency before interaction

forces are encountered, it will be excited oﬀ-resonance after they are encountered.

This, in turn, changes the amplitude and phase (see (6.12) and (6.13)), which serve

as the measurementsignals. Consequently, a diﬀerentamplitude will cause a change

in the encountered eﬀective force. We can see already from this simple gedanken-

experimentthat the interpretationof forcecurves will behighly complicated.In fact,

no quantitative theory for AM-AFM that allows the experimentalist to convert the

experimental data to a force–distance relationship unambiguously is available.

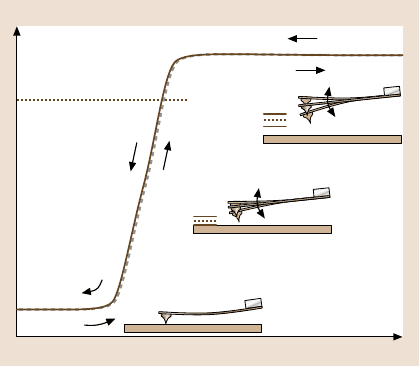
The qualitative behavior for amplitude versus z

-position curves is depicted in

Fig. 6.9. At large distances, where the forces betweenthe tip and the sample are neg-

ligible, the cantilever oscillates with its free oscillation amplitude. As the probe ap-

proaches the surface the interaction forces cause the amplitude to change, typically

resulting in an amplitude that decreases with continuously decreasing tip–sample

distance. This is expected, since the force–distance curve will eventually reach the

repulsive part and the tip is hindered from indenting further into the sample, result-

ing in smaller oscillation amplitudes.

However, in order to gain some qualitative insight into the complex relation-

ship between forces and oscillation parameters, we resort to numerical simulat-

ions. Anczykowski et al. [17, 18] have calculated the oscillation trajectory of the

cantilever under the inﬂuence of a given force model. Van der Waals interactions

were considered the only eﬀective, attractive forces, and the total interaction re-

Amplitude

z-position

Set-point

Fig. 6.9. Simpliﬁed model

showing the oscillation am-

plitude in tapping-mode AFM

for various probe–sample dis-

tances

250 A. Schirmeisen et al.

sembled a Lennard–Jones-type potential. Mechanical relaxations of the tip and

sample surface were treated in the limits of continuum theory with the numerical

Muller-Yushchenko-Derjaguin/Burgess-Hughes-White (MYD/BHW) [19,20] ap-

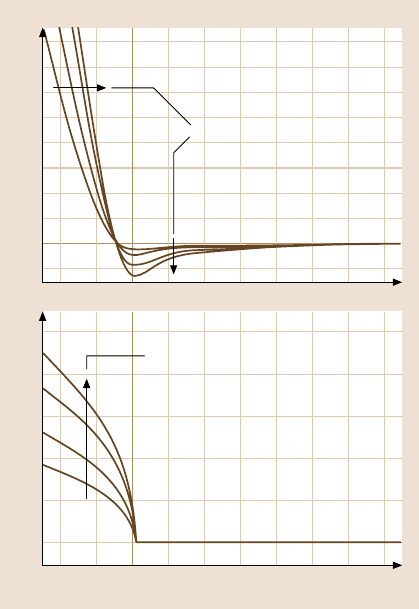
proach, which allows the simulations to be compared to experiments. Figure 6.10

shows the corresponding force–distance curves used in the simulations for diﬀerent

tip radii.

The cantilever trajectory was analyzed by solving the diﬀerential equation (6.7)

extended by the force–distance relations from Fig. 6.10 using the numerical Verlet

algorithm [21,22]. The results of the simulation for the amplitude and phase of the

tip oscillation as a function of z-position of the probe are presented in Fig. 6.11.

One has to keep in mind that the z-position of the probe is not equivalent to the real

tip–sample distance at the equilibrium position, since the cantilever might bend stat-

ically due to the interaction forces. The behavior of the cantilevercan be subdivided

into three diﬀerent regimes. We distinguish the cases in which the beam is oscillated

below its resonant frequency ω

, exactly at ω

,andaboveω

. In the following, we

will refer to ω

as the resonant frequency, although the correct resonant frequency

is ω

∗

if one takes into account the ﬁnite Q-value.

–10

5.0

4.0

3.0

2.0

1.0

0.0

– 0.4 – 0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4

Force (nN)

Contact radius (nm)

Tip-sample distance (nm)

R = 5/10/20/30 nm

Fig. 6.10. Force curves and

corresponding contact ra-

dius calculated with the

MYD/BHW model as a func-

tion of tip radius for a Si–Si

contact. These force curves

are used for the tapping-mode

AFM simulations

6 Dynamic Modes of Atomic Force Microscopy 251

22 24 26

Amplitude (nm)

Phase (deg)

Force (nN)

ω < ω

ω = ω

ω > ω

b) c)

z-position (nm)

135

180

0 10203040

z-position (nm)

0 10203040

z-position (nm)

0 10203040

Amplitude (nm)

Phase (deg)

Force (nN)

135

180

Amplitude (nm)

Phase (deg)

Force (nN)

135

180

ret

app

ret

app

ret

app

ret

app

ret

app

ret

app

ret

app

ret

app

ret

app

ret

Fig. 6.11. Amplitude and phase diagrams with excitation frequency (a)below(b) exactly at

and (c) above the resonant frequency for tapping-mode AFM from the numerical simulations.

Additionally, the lower diagrams show the interaction forces at the point of closest tip–sample

distance, i.e. the lower turnaround point of the oscillation

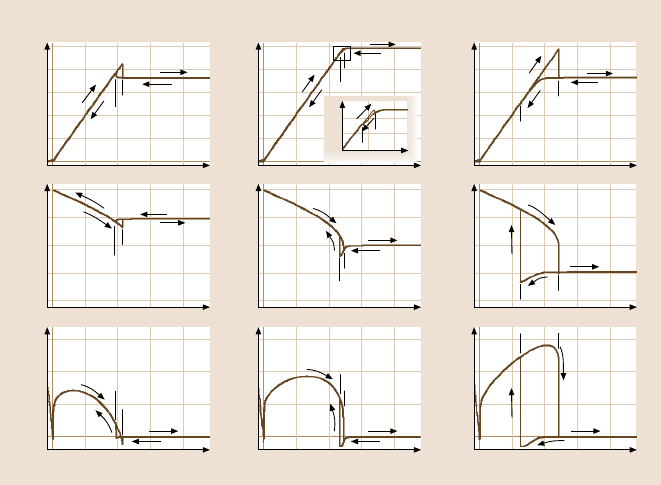
Clearly, Fig. 6.12 exhibits more features than were anticipated from the initial,

simple arguments. Amplitude and phase seem to change rather abruptly at certain

points when the z

-position is decreased. Besides, the amplitude or phase–distance

curves do not resemble the force–distance curves from Fig. 6.11 in a simple, direct

manner. Additionally, we ﬁnd a hysteresis between approach and retraction.

As an example, let us start by discussing the discontinuousfeatures in the AFM

spectroscopy curves of the ﬁrst case, where the excitation frequency is smaller than

. Consider the oscillation amplitude as a function of the excitation frequency in

Fig. 6.5 in conjunction with a typical force curve, as depicted in Fig. 6.10. Upon

approach of probe and sample, attractive forces will lower the eﬀective resonant

frequency of the oscillator. Therefore, the excitation frequency will now be closer

to the resonant frequency, causing the vibration amplitude to increase. This, in turn,

reduces the tip–sampledistance, which againgives rise to a strongerattractiveforce.

The system becomes unstable until the point z

= d

app

is reached, where repulsive

forces stop the self-enhancing instability. This can be clearly observed in Fig. 6.11a.

Large parts of the force–distance curve cannot be measured due to this instability.

In the second case, where the excitation equals the free resonant frequency, only

a small discontinuity is observed upon reduction of the z-position. Here, a shift of