Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

the coefﬁcient of friction which then can be used to convert the friction proﬁle to the coefﬁcient of

friction proﬁle. Thus any directionality and local variations in friction can be easily measured. In this

method, since topography data are not affected by friction, accurate topography data can be measured

simultaneously with friction data and a better localized relationship between the two can be established.

1.3.3.5.2 Normal Force and Friction Force Calibrations

Based on Ruan and Bhushan (1994a), we now discuss normal force and friction force calibrations. In

order to calculate the absolute value of normal and friction forces in newtons using the measured AFM

and FFM

voltage signals, it is necessary to ﬁrst have an accurate value of the spring constant of the

cantilever (k

). The spring constant can be calculated using the geometry and the physical properties of

the cantilever material (Albrecht et al., 1990; Meyer and Amer, 1990b; Sarid and Elings, 1991). However,

the properties of the PECVD Si

(used in fabricating cantilevers) could be different from those of bulk

material. For example, by using an ultrasonic measurement, we found the Young’s modulus of the

cantilever beam to be about 238 ± 18 GPa, which is less than that of bulk Si

(310 GPa). Furthermore,

the thickness of the beam is nonuniform and difﬁcult to measure precisely. Because the stiffness of a

beam goes as the cube of thickness, minor errors in precise measurements of thickness can introduce

substantial stiffness errors. Thus one should experimentally measure the spring constant of the cantilever.

Cleveland et al. (1993) measured the normal spring constant by measuring resonant frequencies of the

beams.

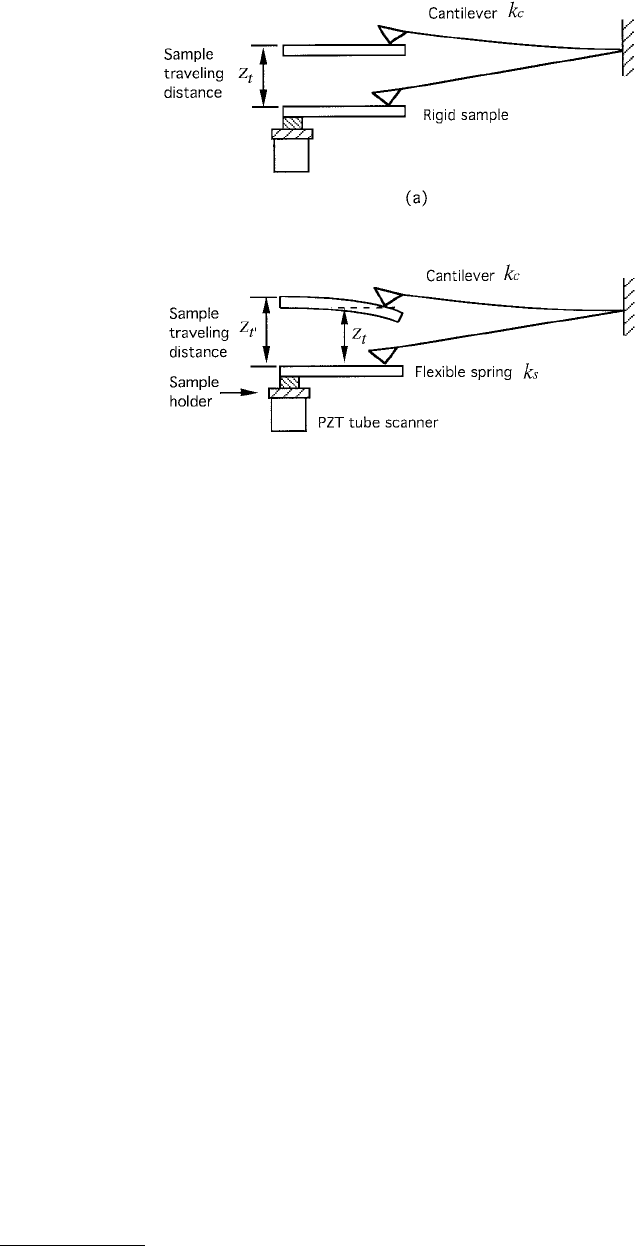
For normal spring constant measurement, we used a stainless steel spring sheet of known stiffness

(width = 1.35 mm, thickness = 15 µm, free hanging length = 5.2 mm) (Ruan and Bhushan, 1994a). One

end of the spring was attached to the sample holder and the other end was made to contact with the

cantilever tip during the measurement, see Figure 1.36. We measured the piezo traveling distance for a

given cantilever deﬂection. For a rigid sample (such as diamond), the piezo traveling distance Z

(measured

from the point where the tip touches the sample) should equal the cantilever deﬂection. To keep the

cantilever deﬂection at the same level using a ﬂexible spring sheet, the new piezo traveling distance Z

t′

would be different from Z

. The difference between Z

t′

. and Z

corresponds to the deﬂection of the spring

sheet. If the spring constant of the spring sheet is k

, the spring constant of the cantilever k

can be

calculated by

FIGURE 1.36 Illustration showing the deﬂection of cantilever as it is pushed by (a) a rigid sample or by (b) a

ﬂexible spring sheet. (From Ruan, J. and Bhushan, B. (1994), ASME J. Tribol., 116, 378–388. With permission.)

(1.8)

The spring constant of the spring sheet (k

) used in this study is calculated to be 1.54 N/m. For a wide-

legged cantilever used in our study (length = 115 µm, base width = 122 µm, leg width = 21 µm, and

thickness = 0.6 µm), k

was measured to be 0.40 N/m instead of 0.58 N/m reported by its manufacturer,

Digital Instruments Inc. To relate photodiode detector output to the cantilever deﬂection in nanometers,

we used the same rigid sample to push against the AFM tip. Because in a rigid sample the cantilever

vertical deﬂection equals the sample traveling distance measured from the point where the tip touches

the sample, the photodiode output as the tip is pushed by the sample can be converted directly to

cantilever deﬂection. For our measurements, we found the conversion to be 20 nm/V.

The normal force applied to the tip can be calculated by multiplying the cantilever vertical deﬂection

by the lever spring constant for samples which have very small adhesive force with the tip. If the adhesive

force between the sample and the tip is large, it should be included in the normal force calculation. This

is particularly important in atomic-scale force measurement because in this region, the typical normal

force that we measure is in the range of a few hundred nanonewtons to a few millinewtons. The adhesive

force could be comparable to the applied force. The magnitude of the adhesive force is determined by

multiplying the maximum cantilever deﬂection in the downward direction before the tip is pulled off

the sample surface by the spring constant of the cantilever. Figure 1.37 shows an example of cantilever

deﬂection as a function of sample position (height). “Extending” means the sample is pushed toward

the tip, and “retracting” means the sample is pulled away from the tip. As the sample surface approaches

the tip within a few nanometers (point A), an attractive force exists between the atoms of the tip surface

and the atoms of the sample surface. The tip is pulled toward the sample and the contact occurs at point

B. As the sample is pushed further against the tip, the force at the interface increases and the cantilever

is deﬂected upward. This deﬂection equals the sample traveling distance measured from point B for a

FIGURE 1.37 Displacement curve of the cantilever tip as it is pushed toward (extending) and pulled away from

(retracting) a silicon sample in measurements made in the ambient environment. The large separation between point

B where the tip is touching the sample and point C where the tip is pulled off the sample is due to a large pull-off

(adhesive) force between the tip and the sample. (From Ruan, J. and Bhushan, B. (1994), ASME J. Tribol., 116,

378–388. With permission.)

ZZkZk

ttstc

′

−

()

kkZ ZZ

cst t t

=−

()

′

rigid sample. As the sample is retracted, the force is reduced. At point C in the retracting curve, the

sample is disengaged from the tip. Before the disengagement, the tip is pulled downward due to the

attractive force. The force that is required to pull the tip away from the sample is the force that equals

(but in the opposite direction) the adhesive force. This force is calculated by the maximum cantilever

deﬂection in the downward direction times the spring constant of the cantilever. The maximum cantilever

deﬂection in downward direction is just the horizontal distance between points B and C in this curve.

We measured this distance to be about 200 nm in this curve, which corresponds to an adhesive force of

80 nN for a spring constant of 0.4 N/m. Friction force at a zero cantilever deﬂection is associated with

this force between the sample and the tip. Because the calculation of both the externally applied and

adhesive forces involves the same spring constant of the cantilever, the total normal force (once the sample

and the tip are in contact) is equal to the spring constant times the cantilever “deﬂection” measured right

before the pull-off point in the retracting curve. This “deﬂection” is also the piezo traveling distance

measured from point C toward the tip for a rigid sample. Although the calculation of adhesive force is

important in the calculation of normal force, it is not important in the calculation of the coefﬁcient of

friction if we take the slope of friction force vs. normal force curve.

The conversion of the friction signal (from FFM

to friction force) is not as straightforward. For

example, one can calculate the degree of twisting for a given friction force using the geometry and the

physical properties of the cantilever (Meyer and Amer, 1988; O’Shea et al., 1992). One would need the

information on the detectors such as the quantum efﬁciency of the detector, the laser power, the instru-

ment gain, etc. in order to be able to convert the signal into the degree of twisting. Generally speaking,

this procedure cannot be accomplished without having some detailed information about the instrument.

This information is not usually provided by the manufacturers. Even if this information is readily

available, errors may still occur in using this approach because there will always be variations as a result

of the instrumental setup. For example, it has been noticed that the measured FFM

signal could be

different for the same sample when different AFM microscopes of the same kind are used. The essence

is that one cannot calibrate the instrument experimentally using this calculation. O’Shea et al. (1992)

did perform a calibration procedure in which the torsional signal was measured as the sample is displaced

a known distance laterally while ensuring that the tip does not slide over the surface. However, it is

difﬁcult to verify that the tip sliding does not occur.

Apparently, a new method of calibration is required. There is a more direct and simpler way of doing

this. The ﬁrst method described (method 1) to measure friction can directly provide an absolute value

of the coefﬁcient of friction. It can therefore be used just as an internal means of calibration for the data

obtained using method 2 or for a polished sample which introduces least error in friction measurement

using method 1. Method 1 can be used to obtain calibration for friction force for method 2. Then this

calibration can be used for measurement on all samples using method 2. In method 1, the length of the

cantilever required can be measured using an optical microscope; the length of the tip can be measured

using an SEM. The relative angle between the cantilever and the horizontal sample surface can be

measured directly. Thus, the coefﬁcient of friction can be measured with few unknown parameters. The

friction force can then be calculated by multiplying the coefﬁcient of friction by the normal load. The

FFM

signal obtained using method 2 can then be converted into friction force. For our instrument, we

found the conversion to be 8.6 nN/V.

1.3.3.5.3 Typical Friction Data

Ruan and Bhushan (1994a) measured the friction of Pt (calibration grid with 10 × 10 µm grid dimension

from Digital Instruments, Inc., with rms roughness of 0.22 nm over 1-mm

area), single-crystal silicon

(rms roughness of 0.14 nm over 1-µm

area), polished natural diamond (IIa); (rms roughness of 2.3 nm

over 1-µm

area), and HOP graphite against an Si

tip using both methods 1 and 2. An engineering

material Al was also measured for reference. Samples were ultrasonically cleaned in alcohol and dried

for a few hours before measurement. The result on Pt (measured using both methods 1 and 2) is used

to calibrate the friction data of other samples obtained using method 2. These data were compared with

those obtained using method 1 for each sample (except graphite and aluminum) to examine the consis-

tency between these two methods.

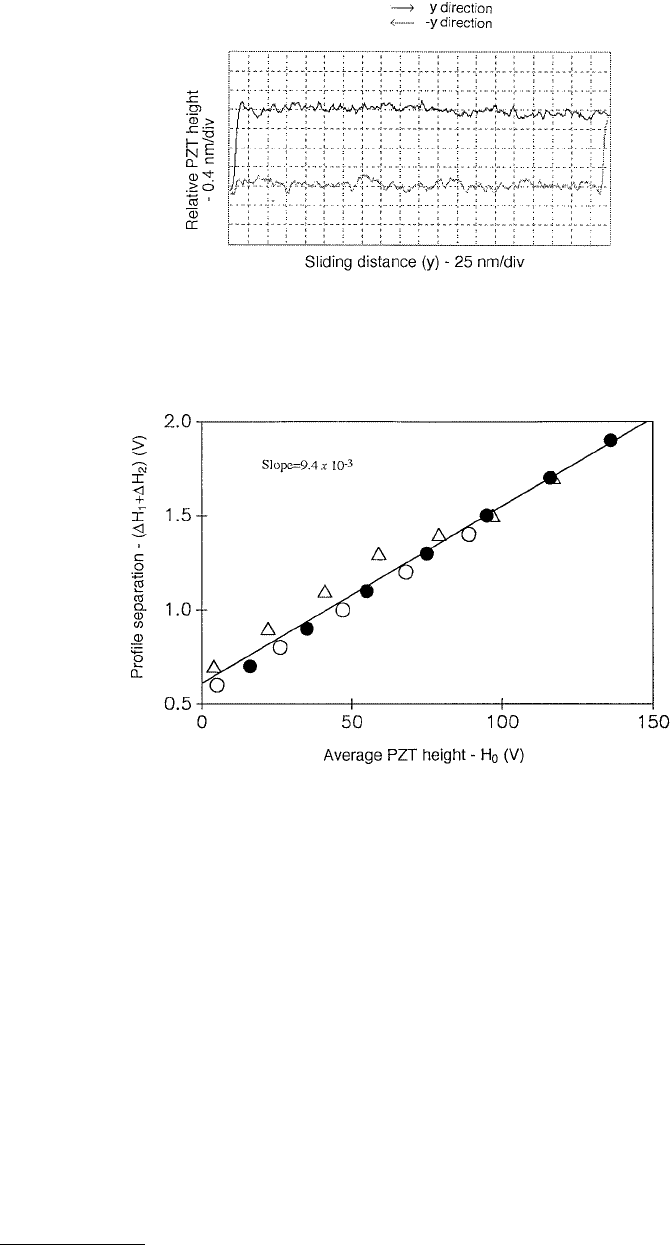
We ﬁrst show in Figure 1.38 an example of a typical trajectory of the piezo vertical height as the AFM

tip is scanned in both the y- and –y-directions across a Pt surface. For a smooth sample like this, the

separation between these two trajectories can easily be measured. We have measured the height difference

of the piezo (∆H

+ ∆H

) at different normal loads (H

), and used ∆ (∆H

+ ∆H

) and ∆(H

) in

Equation 1.5 to calculate µ. Figure 1.39 shows the data from three sets of measurements at various loads

on Pt. The horizontal axis is the center position of the piezo scanner and the vertical axis is the average

(over a 1-mm scan length) height difference of the piezo between the y and –y scans. During the

measurement, the piezotube center position is changed by setting the [(T – B)/(T + B)] signal at different

values for the feedback circuit. The resulting height difference of the piezotube between the two scans

FIGURE 1.38 A typical proﬁle of the piezo height as a Pt sample is scanned back and forth in the y- and –y-

directions. The normal load is about 50 nN. The cantilever stiffness is 0.4 N/m. (From Ruan, J. and Bhushan, B.

(1994), ASME J. Tribol., 116, 378–388. With permission.)

FIGURE 1.39 The vertical height difference (separation of the surface proﬁle, ∆H

+ ∆H

) as a function of the

piezo center position (piezo height H

) between the two traveling directions (y and –y) of a Pt sample. The three

symbols represent three sets of repeated measurements. The slope of the linear ﬁt is proportional to the coefﬁcient

of friction between the Si

tip and Pt. (From Ruan, J. and Bhushan, B. (1994), ASME J. Tribol., 116, 378–388. With

permission.)

(y and –y) was measured and averaged over the scan length. We see in Figure 1.30 that all data fall closely

on a straight line. The slope (best linear ﬁt) of this curve is 9.4 × 10

–3

. Using the geometry of the cantilever

and the tip and attitude of the cantilever with respect to the sample (L = 115 mm, l = 10 mm in

Equation 1.4), a value of the coefﬁcient of friction of 0.054 is obtained.

Figure 1.40 is obtained for Pt using method 2. Here, the cantilever vertical deﬂection vs. the friction

signal (half of the difference of the FFM signals between the x- and –x-scans, or FFM

(x) signal) is

plotted. The sample was moved in the x- and –x-direction at a velocity of 4 µm/s and slowly stepped (by

4 nm/step) in the y-direction (16 nm/s) to scan the whole area (1 × 1 µm). The data (averaged over the

scan area) for each measurement can be ﬁtted into a straight line. To show the statistical variation between

different measurements, 11 sets of measurements at various loads were made and were plotted in this

ﬁgure. Again, a good linear ﬁt of the data has been observed with a slope of 2.5 mV/nm. Using the value

of the coefﬁcient of friction calculated previously, we calculate that a slope of 1 mV/nm in this curve

corresponds to a coefﬁcient of friction 0.022. Using the spring constant of the cantilever (0.4 N/m), we

then calculated that 1 V in this curve (FFM

signal) corresponds to a friction force of 8.6 nN.

Ruan and Bhushan (1994a) made similar measurements on silicon and diamond. They used the values

obtained above for Pt, and the slopes of the curves of these two samples (silicon and diamond) obtained

using method 2 to calculate their coefﬁcient of friction. The data were compared with those obtained

directly using method 1 for the corresponding samples. For simplicity, we summarize the result in

Ta bl e 1.4. A reasonable agreement between the measurements using the two methods was obtained.

Friction data for graphite and aluminum are also included in Table 1.4. (For graphite data, also see Ruan

and Bhushan, 1994b–c.) Method 1 was not used for these samples since a good agreement has already

been obtained between methods 1 and 2 using other samples. In addition, the aluminum sample was

not polished and had a rough surface. Method 1 is difﬁcult to apply to this sample. The friction force

for all tips against graphite was so small that it could not be directly measured using method 1. Even

with method 2, we found that the signal variation at different applied normal forces was also within the

range of experimental uncertainty. The slope that best ﬁts to the data with an uncoated tip is 3 × 10

–4

(V/nm), which corresponds to a coefﬁcient of friction 0.006. This value is listed in Table 1.4. (The

coefﬁcient of friction of graphite against a tungsten tip was reported to be 0.012, according to Mate et al.,

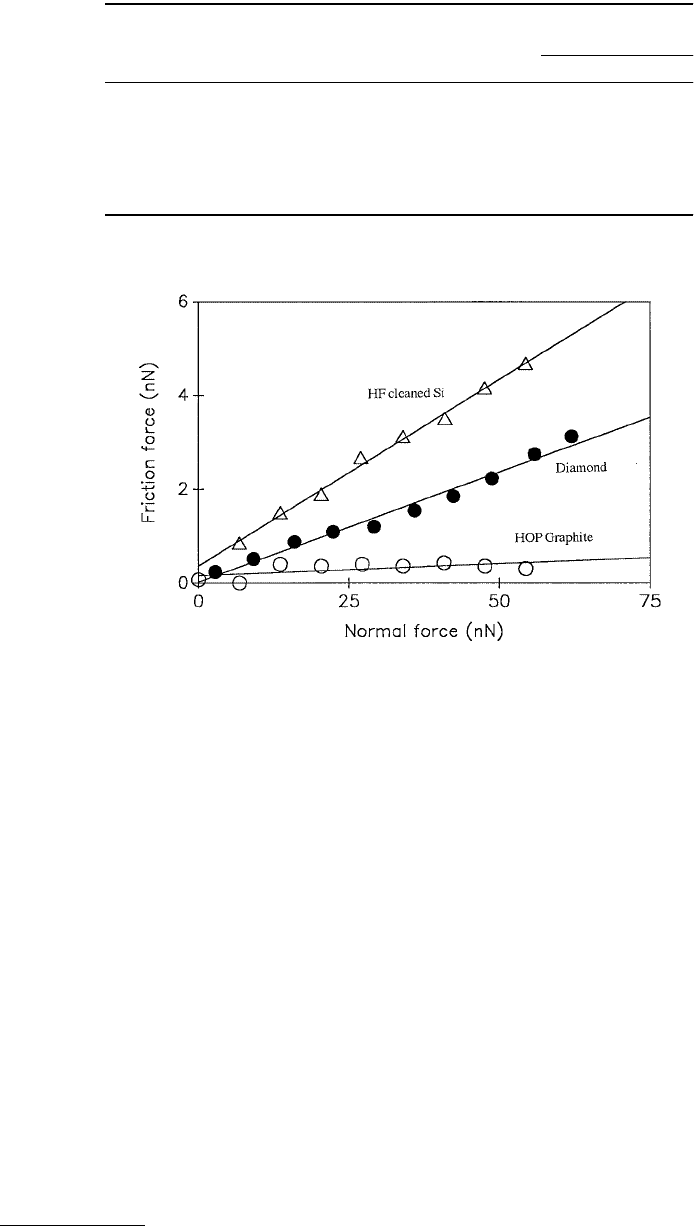
1987). Friction force vs. normal force plots for diamond, HF-cleaned silicon, and graphite are shown in

Figure 1.41.

FIGURE 1.40 Friction signal as a function of cantilever vertical deﬂection for Pt. Different symbols represent 11

sets of repeated measurements. The slope of the linear ﬁt is proportional to the coefﬁcient of friction between the

tip and Pt. Vertical cantilever vertical spring constant is 0.4 N/m with conversion of AFM signal to be 20 nm/V

and the FFM (friction) signal is 8.6 nN/V. (From Ruan, J. and Bhushan, B. (1994), ASME J. Tribol., 116, 378–388.

With permission.)

Figure 1.42 shows atomic-scale friction proﬁles of freshly cleaved HOP graphite. It is clearly seen that

the friction proﬁle exhibits the periodicity of the graphite surface structure (Figure 1.20A). However, the

high points in the topography and the high friction points are shifted relative to each other (Ruan and

Bhushan, 1994b).

1.3.4 Surface Force Apparatus

SFAs are used to study both static and dynamic properties of the molecularly thin liquid ﬁlms sandwiched

between two molecularly smooth surfaces. The SFAs were originally developed by Tabor and Winterton

(1969) and later by Israelachvili and Tabor (1972) to measure van der Waals forces between two mica

surfaces as a function of separation in air or vacuum. Israelachvili and Adams (1978) developed a more-

advanced apparatus to measure normal forces between two surfaces immersed in a liquid so thin that

their thickness approaches the dimensions of the liquid molecules themselves. A similar apparatus was

also developed by Klein (1980). The SFAs, originally used in studies of adhesive and static interfacial

forces, were ﬁrst modiﬁed by Chan and Horn (1985) and later by Israelachvili et al. (1988) and Klein

et al. (1991) to measure the dynamic shear (sliding) response of liquids conﬁned between molecularly

smooth optically transparent mica surfaces. Optically transparent surfaces are required because the

surface separation is measured using an optical interference technique. Van Alsten and Granick (1988)

and Peachey et al. (1991) developed a new friction attachment which allows for the two surfaces to be

TABLE 1.4 Roughness and Microscale Friction Data of Various Samples

Coefﬁcient of Friction

FFM Measurements

Sample Roughness

(nm) Method 1 Method 2

Platinum 0.22 0.05 0.05

Single-crystal silicon (HF cleaned) 0.14 0.07 0.08

Single-crystal silicon (before HF cleaning) 0.14 0.06 0.06

Polished natural diamond (IIa) 2.3 0.04 0.05

HOP graphite 0.09 ~0.006

Aluminum 40 0.08

Root mean square value measured over a 1 × 1 µm area using AFM.

FIGURE 1.41 Friction force as a function of normal force for an Si

tip sliding against silicon, diamond, and

graphite. (From Ruan, J. and Bhushan, B. (1994), ASME J. Tribol., 116, 378–388. With permission.)

sheared past each other at varying sliding speeds or oscillating frequencies while simultaneously mea-

suring both the friction force and normal force between them. Israelachvili (1989) and Luengo et al.

(1997) have also presented modiﬁed SFA designs for dynamic measurements at oscillating frequencies.

Because the mica surfaces are molecularly smooth, the actual area of contact is well deﬁned and mea-

surable, and asperity deformation does not complicate the analysis. During sliding experiments, the area

of parallel surfaces is very large compared to the thickness of the sheared ﬁlm and this provides an ideal

condition for studying shear behavior, because it permits one to study molecularly thin liquid ﬁlms whose

thickness is well deﬁned to the resolution of an angstrom. Molecularly thin liquid ﬁlms cease to behave

as a structural continuum with properties different from that of the bulk material (Van Alsten and

Granick, 1988, 1990b; Homola et al., 1989; Gee et al., 1990; Granick, 1991).

Tonck et al. (1988) and Georges et al. (1993) developed an SFA used to measure the static and dynamic

forces (in the normal direction) between a smooth fused borosilicate glass against a smooth and ﬂat

silicon wafer. They used the capacitance technique to measure surface separation; therefore, use of

optically transparent surfaces was not required. Among others, metallic surfaces can be used at the

interface. Georges et al. (1994) modiﬁed the original SFA so that a sphere can be moved toward and away

from a plane and can be sheared at constant separation from the plane, for interfacial friction studies.

For a detailed review of various types of SFAs, see Israelachvili (1989, 1991), Horn (1990), and Homola

(1993). SFAs based on their design are commercially available from Anutech Pte Ltd., GPO Box 4,

Canberra, Australia 2601.

1.3.4.1 Israelachvili’s and Granick’s Design

The following review is primarily based on the papers by Israelachvili (1989) and Homola (1993).

Israelachvili et al.’s design, later followed by Granick et al., for oscillating shear studies is most commonly

used by researchers around the world.

1.3.4.1.1 Classical SFA

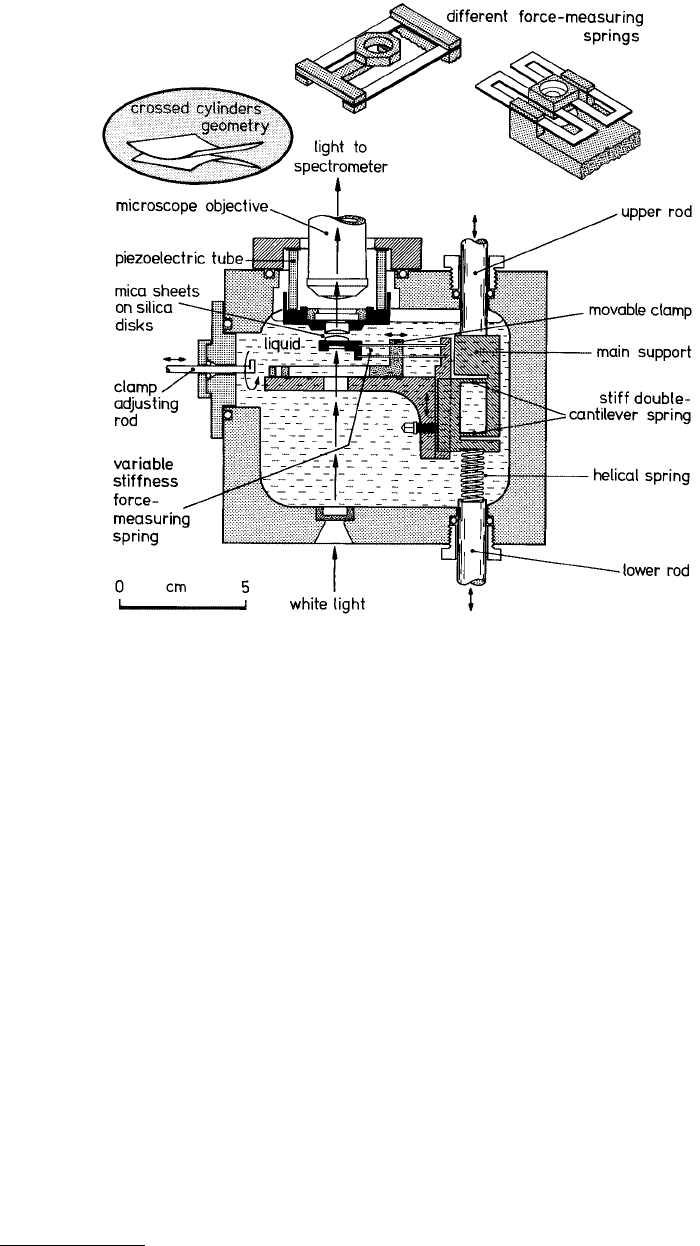
The classical apparatus developed for measuring equilibrium or static intersurface forces in liquids and

vapors by Israelachvili and Adams (1978) consists of a small, airtight stainless steel chamber in which

two molecularly smooth curved mica surfaces can be translated toward or away from each other, see

Figure 1.43. The distance between the two surfaces can also be independently controlled to within

FIGURE 1.42 Gray scale plot of friction proﬁle of a 1 × 1 nm area of a freshly cleaved HOP graphite showing the

atomic-scale variation of topography and friction. Data were taken using a square pyramidal Si

tip. Higher points

are shown by lighter color. (From Ruan, J. and Bhushan, B. (1994), J. Appl. Phys., 76, 5022–5035. With permission.)

For atomic-scale variations in topography, see Figure 1.20a.

±0.1 nm and the force sensitivity is about 10 nN. The technique utilizes two molecularly smooth mica

sheets, each about 2 µm thick, coated with a semireﬂecting 50- to 60-nm layer of pure silver, glued to

rigid cylindrical silica disks of radius about 10 mm (silvered side down) mounted facing each other with

their axes mutually at right angles (crossed-cylinder position), which is geometrically equivalent to a

sphere contacting a ﬂat surface. The adhesive glue which is used to afﬁx the mica to the support is

sufﬁciently compliant, so the mica will ﬂatten under the action of adhesive forces or applied load to

produce a contact zone in which the surfaces are locally parallel and planar. Outside of this contact zone

the separation between surfaces increases and the liquid, which is effectively in a bulk state, makes a

negligible contribution to the overall response. The lower surface is supported on a cantilever spring

which is used to push the two surfaces together with a known load. When the surfaces are forced into

contact, they ﬂatten elastically so that the contact zone is circular for the duration of the static or sliding

interactions. The surface separation is measured using optical interference fringes of equal chromatic

order (FECO) which enables the area of molecular contact and the surface separation to be measured to

within 0.1 nm. For measurements, white light is passed vertically up through the two mica surfaces and

the emerging beam is then focused onto the slit of a grating spectrometer. From the positions and shapes

of the colored FECO fringes in the spectrogram, the distance between the two surfaces and the exact

shape of the two surfaces can be measured (as illustrated in Figure 1.44), as can the refractive index of

the liquid (or material) between them. In particular, this allows for reasonably accurate determinations

of the quantity of material deposited or adsorbed on the surfaces and the area of contact between two

molecularly smooth surfaces. Any changes may be readily observed in both static and sliding conditions

FIGURE 1.43 Schematic of the SFA that employs the cross-cylinder geometry. (From Israelachvili, J.N. and Adams,

G.E. (1978), Chem. Soc. J. Faraday Trans. I, 74, 975–1001; and Israelachvili, J.N. (1989), Chemtracts Anal. Phys. Chem.,

1, 1–12. With permission.)

in real time (applicable to the design shown in Figure 1.44) by monitoring the changing shapes of these

fringes.

The distance between the two surfaces is controlled by use of a three-stage mechanism of increasing

sensitivity: coarse control (upper rod) allows positioning of within about 1 µm, the medium control

(lower rod, which depresses the helical spring and which in turn bends the much stiffer double-cantilever

spring by 1/1000 of this amount) allows positioning to about 1 nm, and the piezoelectric crystal tube —

which expands or controls vertically by about 0.6 nm/V applied axially across the cylindrical wall — is

used for ﬁnal positioning to 0.1 nm.

The normal force is measured by expanding or contracting the piezoelectric crystal by a known amount

and then measuring optically how much the two surfaces have actually moved; any difference in the two

values when multiplied by the stiffness of the force-measuring spring gives the force difference between

the initial and ﬁnal positions. In this way both repulsive and attractive forces can be measured with a

sensitivity of about 10 nN. The force-measuring springs can be either single-cantilever or double-

cantilever ﬁxed-stiffness springs (as shown in Figure 1.43), or the spring stiffness can be varied during

an experiment (by up to a factor of 1000) by shifting the position of the dovetailed clamp using the

adjusting rod. Other spring attachments, two of which are shown at the top of the ﬁgure, can replace

the variable stiffness spring attachment (top right: nontilting, nonshearing spring of ﬁxed stiffness). Each

of these springs are interchangeable and can be attached to the main support, allowing for greater

versatility in measuring strong or weak and attractive or repulsive forces. Once the force F as a function

of distance D is known for the two surfaces of radius R, the force between any other curved surfaces

simply scales by R. Furthermore, the adhesion energy (or surface or interfacial free energy) E per unit

area between two ﬂat surfaces is simply related to F by the so-called Derjaguin approximation (Israelach-

vili, 1991) E = F/2πR. We note that SFA is one of the few techniques available for directly measuring

FIGURE 1.44 (a) Cross-cylinder conﬁguration of mica sheet, showing formation of contact area. Schematic of the

fringes of equal chromatic order (FECO) observed when two mica surfaces are (b) separated by distance D and (c)

are ﬂattened with a monolayer of liquid between them. (From Homola, A. M. et al. (1990), Wear, 136, 65–83. With

permission.)

equilibrium force laws (i.e., force vs. distance at constant chemical potential of the surrounding solvent

medium) (Israelachvili, 1989). The SFA allows for both weak or strong and attractive or repulsive forces.

Mostly the molecularly smooth surface of mica is used in these measurements (Pashley, 1981); however,

silica (Horn et al., 1989) and sapphire (Horn and Israelachvili, 1988) have also been used. It is also

possible to deposit or coat each mica surface with metal ﬁlms (Christenson, 1988; Smith et al., 1988),

carbon and metal oxides (Hirz et al., 1992), adsorbed polymer layers (Patel and Tirrell, 1989), and

surfactant monolayers and bilayers (Christenson, 1988; Israelachvili, 1987, 1991; Israelachvili and

McGuiggan, 1988). The range of liquids and vapors that can be used is almost endless.

1.3.4.1.2 Sliding Attachments for Tribological Studies

Thus far we have described a measurement technique which allows measurements of the normal forces

between surfaces, that is, those occurring when two surfaces approach or separate from each other.

However, in tribological situations, it is the transverse or shear forces that are of primary interest when

two surfaces slide past each other. There are essentially two approaches used in studying the shear response

of conﬁned liquid ﬁlms. In the ﬁrst approach (constant-velocity friction or steady-shear attachment),

the friction is measured when one of the surfaces is traversed at a constant speed over a distance of several

hundreds of microns (Israelachvili et al., 1988; Homola, 1989; Gee et al., 1990; Homola et al., 1990, 1991;

Klein et al., 1991; Hirz et al., 1992). The second approach (oscillatory-shear attachment) relies on the

measurement of viscous dissipation and elasticity of conﬁned liquids by using periodic sinusoidal oscil-

lations over a range of amplitudes and frequencies (Van Alsten and Granick, 1988, 1990a,b; Peachey

et al., 1991; Hu et al., 1991; Luengo et al., 1997).

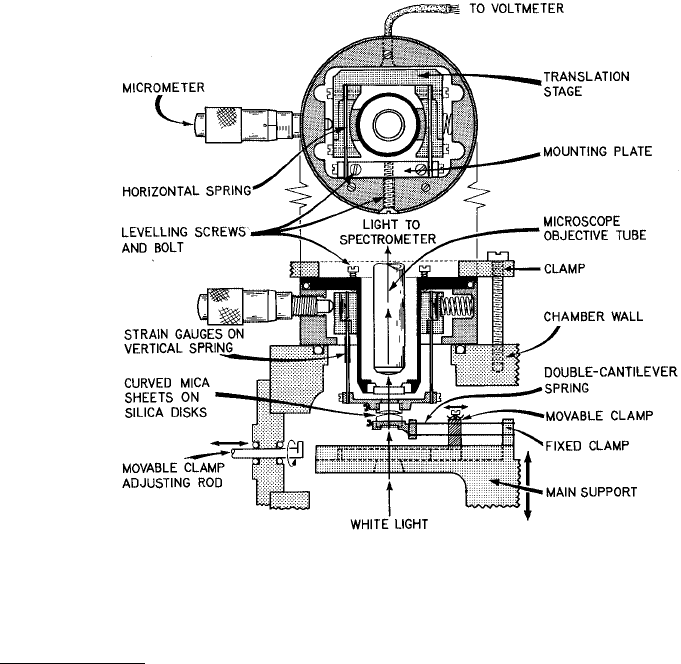
For the constant-velocity friction (steady-shear) experiments, the SFA was outﬁtted with a lateral sliding

mechanism (Israelachvili et al., 1988; Israelachvili, 1989; Homola, 1989; Gee et al., 1990; Homola et al.,

1990, 1991) allowing measurements of both normal and shearing forces (Figure 1.45). The piezoelectric

FIGURE 1.45 Schematic of shear force apparatus. Lateral motion is initiated by a variable-speed motor-driven

micrometer screw that presses against the translation stage which is connected through two horizontal double-

cantilever strip springs to the rigid mounting plate. (From Israelachvili, J.N. et al. (1988), Science, 240, 189–190; and

Israelachvili, J.N. (1989), Chemtracts Anal. Phys. Chem., 1, 1–12. With permission.)