Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

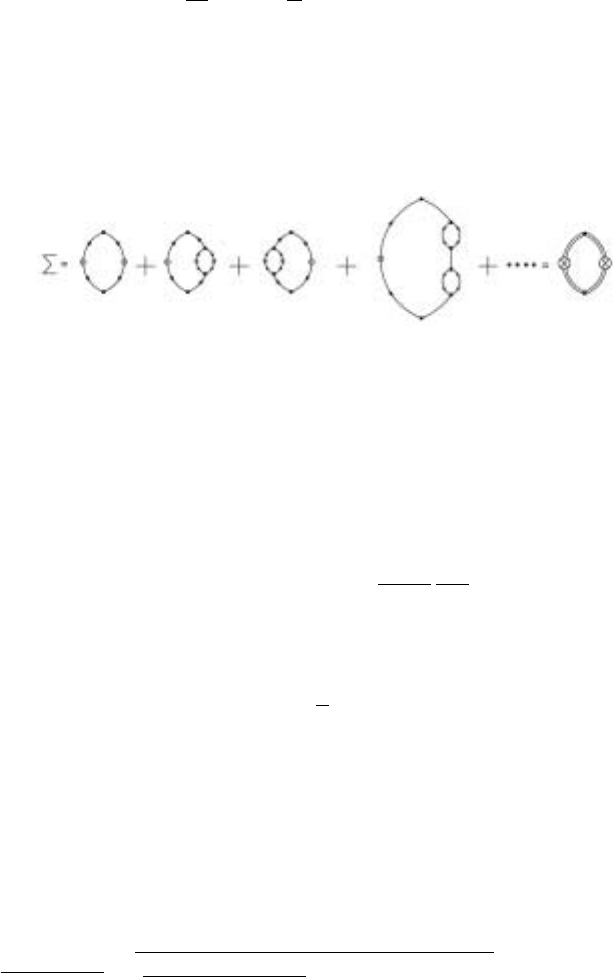
4.3 Spherical Limit 101

of Fig. 4.10c to  is O(

M)=O(

).IfwetakeM →∞limit, this contribution

can be dropped.

Thus, we notice a great simpliﬁcation in the limit M →∞which is dubbed

the spherical limit. The contribution to (k, ω) is given by graph(a) in Fig. 4.10

and all other graphs where the lines of graph(a) are dressed by a graph of the form

shown in graph(a), e.g. the contribution from graph(b). Thus, in the spherical limit,

the graphical expansion of  is as given in Fig. 4.11.

Figure 4.11. Summing the self energy in the spherical limit

which is simply the self consistent mode coupling form of Eq.(4.2.19). If one

is interested in the scaling limit, where the contribution coming from the linear

term in the equation of motion can be dropped,

−1

(k, ω) =−iω +(k, ω) (4.3.5)

corresponding to Fig. 4.11

(k, ω) = g

)



+ω

=ω

p

+p



(2π)

dω

2π

−p

)

× C(p

,ω

)C(p

,ω

) (4.3.6)

and from the FDT

C(k,ω) =

Im G(k, ω) (4.3.7)

In the spherical limit and in the scaling regime, Eqns.(4.3.5)-(4.3.7) constitute an

exact solution to the problem of critical dynamics in the Heisenberg model.

We end this section by a discussion of whether the spherical limit and self

consistent mode coupling are identical. The answer is no. Self consistent mode

coupling can be carried beyond the single loop approximation shown in Fig. 3.9

and indeed it is often necessary to do that in the ﬁeld of dynamic critical phenomena

where the experiments are precise and better accuracy than that providedby Fig. 3.9

is necessary. The spherical limit on the other hand is exact. There are no O(g

)

in this limit. The self consistent mode coupling approximation

of Fig. 3.9 gives an

exact answer

to a generalized problem in the M →∞limit.

References

1. R. Kraichnan, J. Math. Phys. 2 124 (1962)

102 4 Mode Coupling Theories

2. C. Y. Mou and P. Weichman, Phys. Rev. Lett. 70 1101 (1993)

3. J. P. Doherty, M. A. Moore J. M. Kim and A. J. Bray, Phys. Rev. Lett. 72 2041 (1994)

4. L. Sasvari, F. Schwabl and P. Szepfalusy, Physica A81 108 (1975)

5. R

esibois and C. Piette, Phys. Rev. Lett. 24 514 (1970)

6. K. Kawasaki, Ann. Phys(N.Y.) 61 1 (1970)

7. R. A. Ferrell, Phys. Rev. Lett. 24 1169 (1970)

Critical Dynamics in Fluids

5.1 Introduction

We have already encountered the phenomenon of critical slowing down in our

discussion of ferromagnetic transition in chapters 2 and 3. In the study of static

response in second order phase transitions, there is a very strong universality which

tells us that it is only the dimensionality of the order parameter which determines

universality classes. Consequently, the best known critical phenomenon which

is the critical point of a liquid-vapour system (well studied both theoretically and

experimentallyfor about one hundred and twenty ﬁve years) has the same behaviour

as the Ising model which was introduced to study the magnetic transition. The order

parameter (the quantity whose expectation value is zero above the transition and

non-zero below) of the liquid vapour system is the difference between the densities

in the liquid and vapour state. This ﬁeld is a scalar - capable of only being only

positive or negative. The Ising model consists of spins which can point up or down

and thus can be positive or negative and hence in the continuum limit is represented

by a scalar order parameter ﬁeld. The static critical behaviour of the two systems

are consequently identical. For the dynamic responses, this broad universality does

not hold. The liquid-vapour system has nothing to do with the Ising model.

We have already seen evidence of this in our discussion of the ferromagnetic

transition. The Ginzburg-Landau model for a n-component order parameter is ad-

equate for discussing the static responses near the paramagnet- ferromagnet tran-

sition but is totally irrelevant for studying the dynamic responses. The dynamic

response is dictated by reversible terms in the equation of motion for the order

parameter. The reversible terms are so called because they keep the equilibrium

distribution unchanged in time and are simply the physical terms which determine

the dynamics. In our ferromagnet, this simply meant recognizing that the magne-

tization which is the order parameter responds to the torque (magnetization comes

from the ‘angular momentum’) and writing down equations of motion based on

that ensures a correct handling of the dynamics. This is true for all systems showing

104 5 Critical Dynamics in Fluids

dynamic critical behaviour. In this chapter, we discuss the most well-known system

exhibiting critical behaviour from this point of view and then discuss another well

known system - the superﬂuid transition - of liquid

He which gave rise to the

concept of dynamic scaling.

To start our discussion we focus on a system which is in the same universality

class as the liquid-vapour system - this is the symmetric binary mixture. This is a

50 −50 mixture of atoms A and atoms B, which is completely miscible above a

critical temperature T

. Below T

, there is phase separation. If C

is the concentra-

tion of the A atoms and C

the concentration of B atoms, The order parameter is

δC =C

−C

.ForT>T

, δC=0, where the angular brackets denote statisti-

cal averaging. When phase separation occurs for T<T

, δC is clearly non-zero.

Thus δCis clearly the order parameter φ of the transition. This clear cut deﬁnition

of the order parameter makes us choose this as a better example - for the liquid

vapour system the analogue of δC =C

−C

is δρ =ρ

−ρ

, ρ

and ρ

being

the densities in the liquid and gaseous phase. However, experiments show that the

coexistence curve is not symmetric and the order parameter is really a mixture of

density and energy ﬂuctuations. In fact the relevant combination of density and

energy is very much like the entropy.

To discuss the dynamic response in the binary mixture, we imagine the system

to be in equilibrium and then we imagine applying an external force. The force



F per unit mass on every atom A and −



F on every atom B. The system now

settles in to a steady state where there will be a ﬁnite current corresponding to the

concentration difference ψ. The A-current and B-current are equal and opposite

and the current



corresponding to the concentration difference ψ is



−



(5.1.1)

For small values of the force



F , the current is proportional to the force and we can

write



=λ



F (5.1.2)

the constant of proportionality deﬁning the transport coefﬁcient for the concen-

tration difference. The same current can be generated if instead of an external

force, we have a concentration gradient in the system. In this case, the current is

proportional to the gradient of chemical potential and we have



=−λ



∇µ =−=



∇ψ (5.1.3)

where

∂µ

∂ψ



P,T

(5.1.4)

5.1 Introduction 105

is the isothermal susceptibility of the system. The equation of motion for ψ can be

found from the conservation law

∂ψ

∂t

=−



∇.



∇

= D

∇

ψ (5.1.5)

where D

is the familiar concentration diffusion coefﬁcient. In terms of the trans-

port coefﬁcient λ,weﬁnd

. (5.1.6)

The relaxation rate for the Fourier component ψ(k) is clearly D

If instead of a concentration current, we talk about a heat current, then the trans-

port coefﬁcient is the thermal conductivity λ

, the corresponding susceptibility is

the constant pressure speciﬁc heat and for the thermal diffusion coefﬁcient is

. (5.1.7)

For the momentum current, the transport coefﬁcient is the shear viscosity η and the

corresponding susceptibility is simply the density of the system. The momentum

diffusion coefﬁcient is the kinematic viscosity ν and we have

ν =

. (5.1.8)

We now need to discuss what happens to the transport coefﬁcient near the critical

point. Close to the critical point, regions where ﬂuctuations are correlated become

very large and the correlation length ξ which characterizes the system becomes

inﬁnite at T =T

. Close to T =T

, ξ ∼t

−ν

where

t =

T −T

Over a region of size ξ in a D dimensional space, the applied force



f is given by



f =ξ



F (5.1.9)

where



F is the applied force per unit mass. In the steady state, where there is a

uniform velocity v, there is an equal and opposite resistive Stokes’ law force which

is given by



∝vηξ

D−2

(5.1.10)

106 5 Critical Dynamics in Fluids

The current



j is given by



j =ψ v=



2−D







2−D











F (5.1.11)

leading to the transport coefﬁcient

λ =

ψ

. (5.1.12)

The expectation value ψ

 is proportional to the susceptibility per unit volume

and thus

ψ

∝

∝ξ

2−η

−D

. (5.1.13)

From static critical phenomenon

∝ξ

2−η

where η

is the anomalous dimension index, the subscript put to differentiate it

from the shear viscosity η. The transport coefﬁcient is given by

λ =

ψ

∝

4−D−η

(5.1.14)

Assuming that the shear viscosity has no critical variation (or a very weak one

even if it has one, since it is not the response function directly associated with the

order parameter), we see that the transport coefﬁcient diverges for D<4 −η



4(η

O(10

−2

)).

The above discussion shows two things

• i) the transport of order parameter is strongly affected by critical ﬂuctuations

and the transport coefﬁcient diverges at the critical point.

• ii) The velocity ﬂuctuations are involved in the process since the current is

provided by the velocity. The velocity ﬂuctuations are not critical but couple

to the order parameter. Without detailed calculations, it is not possible to say

how the transport of the momentum ﬂuctuations is affected, and what would

be if any, the critical behaviour of the shear viscosity.

5.2 Equations for Transport Coefﬁcients 107

5.2 Equations for Transport Coefﬁcients

We thus see that to proceed further and get a quantitative estimate of the different

transport coefﬁcients, the coefﬁcients associated with concentration ﬂow, the heat

ﬂow, the momentum ﬂow, and also the density ﬂuctuations determining the sound

propagation - equations of motion need to be established. For the concentration

difference ψ for the binary liquid, the equation of motion in Eq.(5.1.5) needs

to be augmented by including the coupling to the velocity ﬁeld. This is a very

straightforward modiﬁcation of the time derivative in Eq.(5.1.5). Instead of the

partial time derivative at a given point in space, we need the total time derivative

which includes the change brought about by the transport by the velocity ﬁeld.

This leads to the equation of motion

∂ψ

∂t

+(v.



∇)ψ =D∇

ψ =

∇

ψ (5.2.1)

We now need to write down the equation of motion for the velocity ﬁeld. This is

the Navier-Stokes equation. For the time being we will ignore the sound wave and

assume incompressible ﬂow i.e.



∇.v =0 (5.2.2)

The velocity ﬂuctuations are small and all ﬂows are in the very low Reynold’s

number regime. So the usual non-linearity (v.



∇)v [and also



∇P , P being the

pressure, which for an incompressible ﬂow is proportional to (v.



∇)v] is negligible

and for the i

component of the velocity vector

∂v

∂t

ij,j

(5.2.3)

where T

is the stress tensor. The usual contribution to the stress tensor is



∂v

∂x

∂v

∂x



What we need to know is how does the concentration ﬂuctuation affect the stress

tensor, because it is through the coupling to the order parameter ﬁeld that we expect

behaviour to arise. To this end, we need to know the equilibrium free energy. This

is the Ginzburg-Landau free energy augmented by a quadratic term in velocity to

account for the probabilistic distribution of the velocity ﬂuctuations. We will drop

the quadratic term in the Ginzburg-Landau free energy since it is not particularly

relevant directly to the dynamics. It’s effect on the statics will be taken care of by

assuming that the mass term in the free energy has the correct critical behaviour.

The free energy F is

F =





(∇ψ)



(5.2.4)

108 5 Critical Dynamics in Fluids

As stated above the term ψ

is missing in F, but its effect on the statics is included

by stipulating that the mass term κ ∝t

where ν is the correct critical exponent

(ν 0.62 for n =1, i.e. scalar order parameter) and t is the reduced temperature

t =

T −T

being the critical point temperature. To ﬁnd the stress tensor, we imagine the

ﬂuid away from the critical point and apply an external potential V(x), to which the

system responds by setting up a spatially dependent ψ(x), such that the contribution

to the energy is ψ(x)V x. The free energy F in the presence of V(x) is

F(ψ,



∇ψ, V (x)) =F(ψ,



∇ψ, V =0) +ψV (5.2.5)

The force



K is obtained from the gradient of F and

=−

∂F

∂x

=−

∂F

∂ψ

∂x

−



∂F

∂



∂ψ

∂x



∂

∂x



∂ψ

∂x



−ψ

∂V

∂x

(5.2.6)

In the presence of V(x), the system will have to adjust itself to minimize



F(ψ,



∇ψ, V (x))d

and that leads to the canonical Euler-Lagrange equation

∂F

∂ψ



∂

∂x



∂F

∂(

∂ψ

∂x

)



(5.2.7)

Using this condition in Eq.(5.2.6)

=−



∂

∂x



∂F

∂(

∂ψ

∂x

)



∂ψ

∂x

−





∂F

∂(

∂ψ

∂x

)



∂

∂x



∂ψ

∂x



−ψ

∂V

∂x

=−



∂

∂x



∂F

∂(

∂ψ

∂x

)



∂ψ

∂x



−ψ

∂V

∂x

=−



∂T

∂x

−ψ

∂V

∂x

(5.2.8)

where



∂F

∂(

∂ψ

∂x

)



∂ψ

∂x

(5.2.9)

For a more general way of ﬁnding the non-linear contribution to the velocity equa-

tion due to concentration ﬂuctuations we need to ensure that the free energy F is

5.2 Equations for Transport Coefﬁcients 109

unaffected by the non-linear terms. With

ψ given in Eq.(5.2.1) we have (keeping

only the non-linear terms in the equation of motion)

0 =

∂

∂t



x =





ρv

˙v

+κ

ψ +

∂ψ

∂x

∂

∂x







ρv

˙v

−κ

ψv

∂ψ

∂x

−

∂ψ

∂x

∂

∂x



∂ψ

∂x







ρv

˙v

−κ

ψv

∂ψ

∂x

∂ψ

∂x

∂

∂x



x (5.2.10)

keeping in mind that v is compressible thus gives the equation of motion (so far as

the non-linear terms go)

ρ ˙v



−

∂ψ

∂x

∂

∂x

+κ

∂ψ

∂x



(5.2.11)

The missing linear term in the above equation comes from the shear contribution

to the stress tensor and

˙v

=ν∇



∂ψ

∂x

−

∂ψ

∂x

∇



(5.2.12)

The deterministic equations shown in Eqns.(5.2.11) and (5.2.12) cannot maintain

the equilibrium distribution because the linear terms are dissipative. These are

hydrodynamic terms and are associated with the long wavelength behaviour. The

short wavelength ﬂuctuations give rise to noise terms in the equations of motion

for ψ and v. These noise terms with appropriate correlations to ensure ﬂuctua-

tion dissipation theorem maintain the equilibrium. The ﬁnal equations of motion,

consequently, are

ψ =

∇

ψ −(v.



∇)ψ +N

(5.2.13)

˙v

= ν∇



∂ψ

∂x

−

∂ψ

∂x

∇



+ N

(5.2.14)

The correlations are

N

(x,t)N

(





)=−2λ∇

δ(x −





)δ(t−t



)

N

(x,t)N

(





)=−2ν∇

δ(x −





)δ(t−t



(5.2.15)

where P

is the projection operator

=δ

−

∂

∂x

which is necessary to maintain the transverse nature of the velocity ﬁeld.

110 5 Critical Dynamics in Fluids

In momentum space, the equations of motion are

ψ(



k) =−

ψ(



k) −i



p

(



k −p) p

ψ(p) + N

(



=−λ(k

+κ

ψ(



k) −i



p

(



k −p) ψ( p) + N

(



k) (5.2.16)

˙v

(



k) =−νk

(



k) +iκ



p

ψ(



k −p) ψ( p)

(k)



p

[(



k −p)

−p

]ψ(



k −p) ψ( p) + N

v

(



k) (5.2.17)

In the above, we have used

−1

+κ

If the non-linear terms are absent, then the Green’s functions and correlation func-

tions can be written down as

(k,κ,ω) =−iω +λ(k

+κ

(0)

(k,κ,ω) =

2λk

+λ

+κ

)

(0)−1

]

= (−iω +ηk

(k)

and [C

(0)

]

2ηk

+η

(k) (5.2.18)

where the momentum space projection operator is

(k) =δ

−

The dynamic critical exponents for the order parameter and velocity ﬁelds are

different at this zeroth level. At the critical point, κ =0, the relaxation rate for

the ψ ﬁeld is λk

, giving z

=4. For the velocity ﬁeld relaxation rate is ηk

giving z

=2. The non-linear terms are likely to affect λ and η, and we use the

self-consistent technique developed in Chapter 4 to ﬁnd the answer in the next

section.

5.3 One-Loop Perturbation Theory

In this section, we will investigate the single loop perturbation theory contribution

to the transport coefﬁcients λ and η. To do so, we ﬁrst look at the lowest order