Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.

3.5 Field Theoretic Form 81
The problem cast in the form of Eqns.(3.5.7) and (3.5.8) looks very much like
the problem in statics - set up a free energy functional (statics) and then evaluate
the partition function. The action S(φ,
˜
φ) of Eq(2.5.8) is the analogue of the free
energy functional and the Z(φ,
˜
φ) of Eq.(3.5.7) is the ‘partition function’.
The physical meaning of the field
˜
φ can be seen from the Eqns(3.5.7) and
(3.5.8), if we add an external force
F to the equation of motion in Eq.(3.5.1). The
response function χ is then given by
χ =
δφ(r
1
,t
1
)
δF(r
2
,t
2
)
f →0
=φ(r
1
,t
1
)
˜
φ(r
2
,t
2
) (3.5.9)
Thus the response function is cast as a correlation function and we can now write
down the response and correlation function by an inspection of the action in mo-
mentum and frequency space.
S =
d
D
k
(2π)
D
dω
2π
[−
˜
φ(k, ω)
˜
φ(−k, −ω)
+
˜
φ(−k, −ω){−iω+(k
2
+m
2
)}
˜
φ(k, ω)] (3.5.10)
Evaluation of the Gaussian functional integral to obtain the correlation function
˜
φ(k, ω)
˜
φ(−k, −ω)and φ(k,ω)φ(−k, −ω)leads to the answers written down
in Eqns.(3.5.4) and (3.5.5).
In general the action will not be quadratic. If we consider the full model A with
the equation of motion given by Eq.(2.4.2) with the free energy given by Eq.(2.4.1),
the action will be
S =
d
D
k
(2π)
D
dω
2π
−
˜
φ(k, ω)
˜
φ(−k, −ω) +
˜
φ(−k, −ω){−iω+(k
2
+m
2
)}
×
˜
φ(k, ω)+u
˜
φ(−k, −ω)
φ(
k −p
1
−p
2
,ω−ω
1
−ω
2
)
× φ(p
1
,ω
1
)φ( p
2
,ω
2
) (3.5.11)
The kinetic coefficient now needs a renormalization constant Z to render the dy-
namic correlations finite because of the quartic term in the action. For the Heisen-
berg model of Eq.(3.4.2), the action will be
S =
d
D
k
(2π)
D
dω
2π
−
˜
φ
α
(k, ω)
˜
φ
α
(−k, −ω) +
˜
φ
α
(−k, −ω)
{−iω +(k
2
+m
2
)}
×
˜
φ
α
(k, ω) −g
p,ω
˜
φ
α
(−k, −ω)
˜
φ
β
(p, ω
)
˜
φ
γ
(
k −p, ω −ω
)
[p
2
−(
k −p)
2
]
(3.5.12)
Once again the non-quadratic term will renormalize the kinetic coefficient and
the calculation will parallel the field theoretic treatment in statics.
82 3 The Renormalization Group
References
Dynamic Renormalization Group
1. K. G. Wilson and J. Kogut, Phys. Rep. 12C 75 (1974)
2. M. N. Barber, Phys. Rep. 29C 1 (1977)
3. M. E. Fisher, “Scaling, Universality and Renormlization Group Theory” in Critical
Phenomena ed. F. J. W. Hahne Springer Lecture Notes, Berlin (1983)
4. J.J. Binney et.al., The Theory of Critical Phenomena, An Introduction to the Renormali-
zation Group. Clarendon Press, Oxford. (1993)
5. R. Shankar Rev. Mod. Phys. 66 129 (1994)
6. P.M. Chaikin and T.C. Lubensky, Principles of Condensed Matter Physics. Cambridge
University Press. (1995)
7. J.L. Cardy, Scaling and Renormalization in Statistical Physics. Cambridge University
Press. (1996)
Dynamic Renormalization Group
8. R. Bausch, H. K. Janssen and H. Wagner Z. Phys. B10 113. (1976)
9. P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys. 49 435 (1977)
10. C. DeDominicis and L. Peliti, Phys. Rev. Lett. 38 505 (1977)
11. T. Halpin-Healy and Y. C. Zhang Phys. Rep. 254 215 (1995).
12. A. L. Barabasi and H. E. Stanley Fractal Concepts in Surface Growth Cambridge
University Press, Cambridge (1995)

4
Mode Coupling Theories
4.1 Introduction
In this chapter, we will deal with two techniques which are non-perturbative in
nature and hence can be very effective in features that may elude perturbation
theory. The implementation of the RG that we discussed in the last chapter often
requires perturbation theory. For a given problem it is consequently a good idea to
try both the RG and the techniques that we will discuss here. We will explain the
method by using the same ferromagnetic system that we used in §3.4. The equation
of motion is
˙
φ
i
(
k) =−
0
k
2
(k
2
+m
2
)φ
i
(k) +N
i
(k)
+g
p
1
+p
2
=
k
ij k
(p
2
1
−p
2
2
)φ
j
( p
1
)φ
k
( p
2
) (4.1.1)
with
N
i
(
k
1
,ω
1
)N
j
(
k
2
,ω
2
)=−2
0
k
2
1
δ
ij
δ(
k
1
+
k
2
)δ(ω
1
+ω
2
) (4.1.2)
By the word mode, one refers to the Fourier mode φ(
k). The non-linear term
in the equation of motion couples the different modes. The second term on the
R.H.S of Eq.(4.1.2) is the non-linear term and as is obvious the term couples the
modes φ(p
1
) and φ( p
2
) with the constraint p
1
+p
2
=
k. The linear term, the first
term on the R.H.S of Eq.(4.1.2), on the other hand, does not couple modes and
consequently the linear equation of motion is trivially solvable. Before discussing
how to handle the non-linear terms we need to discuss some general issues. The
response or Green’s function is defined as
G
ij
(
k, ω)=
δφ
i
(k, ω)
δN
j
(k
,ω)
1
δ(
k +
k
)δ(ω +ω
)
(4.1.3)

84 4 Mode Coupling Theories
and the correlation function by
C
ij
(
k, ω)=φ
i
(
k, ω)φ
j
(
k
,ω
)
1
δ(
k +
k
)δ(ω +ω
)
(4.1.4)
For an isotropic system (both in order parameter space and in actual space time)
and the noise uncorrelated in different directions, we have
G
ij
(
k, ω)=G(k, ω)δ
ij
and similarly,
C
ij
(
k, ω)=C(k,ω)δ
ij
.
In this chapter, we will always assume that the isotropy holds.
The calculation of G becomes straight forward if it can be expressed as a cor-
relation function. Examination of Eq.(4.1.1) shows us that the required correlation
function is
G(k, ω) =(2
0
k
2
)
−1
φ
i
(
k, ω)N(
k
,ω
)
1
δ(
k +
k
)δ(ω +ω
)
(4.1.5)
If we work with the linear part alone, then Eq.(4.1.1) shows that in Fourier space
[−iω +
0
k
2
(k
2
+m
2
)]φ
i
(k, ω) =N
i
(k, ω)
leading to, according to Eq.(4.1.3)
G(k, ω) =[−iω +
0
k
2
(k
2
+m
2
)]
−1
(4.1.6)
If we use Eq.(4.1.5)
G(k, ω) =
1
2
0
k
2
φ
i
(
k, ω)N(
k
,ω
)
1
δ(
k +
k
)δ(ω +ω
)
=
1
2
0
k
2
[−iω +
0
k
2
(k
2
+m
2
)]
−1
N(
k, ω)N(
k
,ω
)
×
1
δ(
k +
k
)δ(ω +ω
)
=[−iω+
0
k
2
(k
2
+m
2
)]
−1
the same as that obtained in Eq.(4.1.6).
The static response function of the system is
χ =
1
k
2
+m
2
4.1 Introduction 85
and it is useful to normalize the dynamic response such that the zero frequency limit
correctly reproduces the statics. We can do this by recognizing that the relaxation
rate
=
0
k
2
(k
2
+m
2
) =
0
k
2
/χ
and thus the desired normalization is obtained if
G(k, ω) =χ
δφ
δN
=
1
2
φN (4.1.7)
Thus, instead of using the definitions given in Eqns.(4.1.3) and (4.1.5), we will
use the prescription in Eq.(4.1.7) which correctly reproduces the static limit. The
normalization of G(k, ω) to the static response is vital for the following discussion.
In statics, the response function is also the two-point correlation function. With this
normalization we will be able to generalize this result to dynamics. Since G(k, ω)
is a response function, it will be causal and in general will satisfy all the conditions
for satisfying the Kramers-Kronig relation and we have
G(k, ω) =
1
π
Im G(k, ω
)
ω
−ω
dω
For the static response,
G(k, 0) =
1
π
Im G(k, ω
)
ω
dω
. (4.1.8)
Turning to the correlation function C(k,ω), the equal time correlation function
C(k,t
12
=0) is obtained from the integral
C(k,t
12
=0) =
dω
2π
C(k,ω
) (4.1.9)
The equal time correlation is the static response function when we have an
equilibrium distribution function. In that case, the equality of the L.H.S of
Eqns.(4.1.8) and (4.1.9) lead to the fluctuation dissipation theorem (FDT).
C(k,ω) =
1
2ω
Im G(k, ω) (4.1.10)
For our linearized system, the correlation function C(k,ω) according to Eq.(4.1.4)
is
C(k,ω) =
2
0
k
2
ω
2
+[
0
k
2
(k
2
+m
2
)]
2
=
1
0
k
2
2
(
ω
0
k
2
)
2
+(k
2
+m
2
)
2
(4.1.11)

86 4 Mode Coupling Theories
With G(k, ω) given by Eq.(4.1.7) as
G(k, ω) =
−
iω
0
k
2
+(k
2
+m
2
)
−1
(4.1.12)
We find that Eq.(4.1.10) is satisfied as expected.
If the FDT is satisfied, then we do not need to consider the equations for G(k, ω)
and C(k,ω) separately, since the information obtained automatically leads to the
information on the other. For systems without an equal time (equilibrium) distri-
bution function, however, the FDT does not hold and G(k, ω) and C(k,ω) must
be separately considered. For the models of dynamic critical phenomena discussed
in Chapter 1, FDT holds and one simply needs to consider the response function
(or correlation function), while for the driven diffusive lattice gas (§2.5) and the
growth models (§2.6), there is no equilibrium distribution and there is no FDT. In
the detailed example that we consider in this chapter - the critical dynamics of the
Heisenberg ferromagnet as given in Eq.(4.1.1) there is an equilibrium distribution,
and the FDT holds. This simplifies our work.
4.2 Self Consistent Mode Coupling
We will now try to find the response function for the dynamics of the Heisenberg
model as represented by Eq.(4.1.1). We begin by working with perturbation theory
by expanding
φ(
k, t) =φ
(0)
i
(
k, t) +g +φ
(1)
i
(
k, t) +g
2
φ
(2)
i
(
k, t) +.... (4.2.1)
Inserting the expansion in Eq.(4.1.1) and equating equal powers of g on either side
of the equation, we have
˙
φ
i
(0)
=−
0
k
2
(k
2
+m
2
)φ
(0)
i
+N
i
(4.2.2)
˙
φ
i
(1)
=
ij k
(p
2
1
−p
2
2
)φ
(0)
j
( p
1
)φ
(0)
k
( p
2
) −
0
k
2
(k
2
+m
2
)φ
(1)
i
(4.2.3)
˙
φ
i
(2)
=−
0
k
2
(k
2
+m
2
)φ
(1)
i
+
ij k
(p
2
1
−p
2
2
)[φ
(0)
j
( p
1
)φ
(1)
k
( p
2
)
+φ
(1)
j
( p
1
)φ
(0)
k
( p
2
)] (4.2.4)
The Green’s function has the expansion
G = G
(0)
+gG
(1)
+g
2
G
(2)
+.......
=
1
2
[φ
(0)
(k, ω)N(−k, −ω)+gφ
(1)
(k, ω)N(−k, −ω)
+g
2
φ
(2)
(k, ω)N(−k, −ω)+.......] (4.2.5)
4.2 Self Consistent Mode Coupling 87
The solution for φ
(0)
i
from Eq.(4.2.2) is
˙
φ
i
(0)
(−
k, t) =e
−
0
k
2
(k
2
+m
2
)t
t
−∞
dt
e
0
k
2
(k
2
+m
2
)t
N(k,t
)
This leads to the zeroth order response as
G
(0)
=
1
2
φ
(0)
i
(
k, t
1
)N
i
(−
k, t
2
)
=
1
2
e
−
0
k
2
(k
2
+m
2
)t
1
t
1
−∞
dt
e
0
k
2
(k
2
+m
2
)t
N
i
(k, t
)N
i
(−k, t
2
)
=
1
2
e
−
0
k
2
(k
2
+m
2
)t
1
2
0
k
2
t
1
−∞
dt
e
0
k
2
(k
2
+m
2
)t
δ(t
−t
2
)
=
0
k
2
e
−
0
k
2
(k
2
+m
2
)(t
1
−t
2
)
θ(t
1
−t
2
)
The Fourier transform
G
(0)
(k, ω) =
∞
−∞
dt
12
G(k, t
12
)e
iωt
12
immediately leads us to the response function given by Eq.(4.1.12)
G
(0)
(k, ω) =[−
iω
0
k
2
+(k
2
+m
2
)]
−1
(4.2.6)
The solution at O(g) (Eq.(4.2.3)) is
φ
(1)
i
(t
1
) = e
−
0
k
2
(k
2
+m
2
)t
1
t
1
−∞
dt
e
0
k
2
(k
2
+m
2
)t
[
ij k
(p
2
1
−p
2
2
)
× φ
(0)
j
( p
1
,t
)φ
(0)
k
( p
2
,t
)]
= e
−
0
k
2
(k
2
+m
2
)t
1
t
1
−∞
dt
e
0
k
2
(k
2
+m
2
)t
[
ij k
(p
2
1
−p
2
2
)
×
e
−
0
p
2
1
(p
2
1
+m
2
)(t
−t
)
N
j
( p
1
,t
)dt
×
e
−
0
p
2
2
(p
2
2
+m
2
)(t
−t
)
N
j
( p
2
,t
)dt
] (4.2.7)
For the response function at O(g),
G
(1)
=
1
2
φ
(1)
i
N
i
= 0 (4.2.8)
88 4 Mode Coupling Theories
The above solution for φ
(1)
i
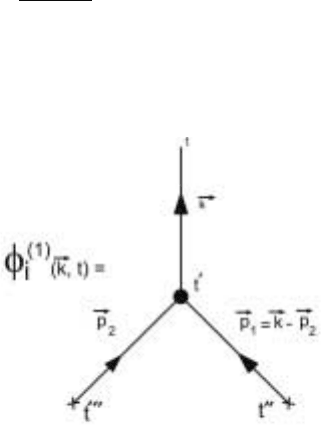
can be expressed graphically as shown in Fig. 4.1. The
cross indicates the noise. With
G
(0)
(t
12
)
0
k
2
= e
−
0
k
2
(k
2
+m
2
)(t
12
)
θ(t
12
)
the lines in the figure corresponding to G
(0)
(t
12
)/
0
k
2
with the arrow in the di-
rection of increasing time and the solid circle corresponds to an interaction.
Figure 4.1. Three point vertex where a magnetic fluctuation at a given wave Vector couples
to two other fluctuations with different wave vectors
Inserting Eq.(4.2.2) and using φ
(1)
i
from Eq.(4.2.5), we have
φ
(2)
(k, t
1
) =
e
−
0
k
2
(k
2
+m
2
)(t
1
−t
)
p
1
+p
2
=
k
ij k
(p
2
1
−p
2
2
)[φ
(1)
j
( p
1
,t
)
× φ
(0)
k
( p
1
,t
) +φ
(0)
j
( p
1
,t
)φ
(1)
k
( p
1
,t
)]dt
=
dt
e
−
0
k
2
(k
2
+m
2
)(t
1
−t
)
p
1
+p
2
=
k
ij k
(p
2
1
−p
2
2
){
dt
dt
× dt
q
1
+q
2
=p
1
e
−
0
p
2
1
(p
2
1
+m
2
)(t
−t
)
e
−
0
q
2
1
(q
2
1
+m
2
)(t
−t
)
× e
−
0
q
2
2
(q
2
2
+m
2
)(t
−t
)
N
k
(q
1
,t
)N
i
(q
2
,t
)
dt
× e
−
0
p
2
2
(p
2
2
+m
2
)(t
−t
)
N
k
(p
2
,t
)
+ an identical term with p
1
↔p
2
. (4.2.9)
The diagrammatic representation of the two terms on the R.H.S of Eq.(4.2.7) would
be,

4.2 Self Consistent Mode Coupling 89
Forming the correlation length with N(−k, t
2
) gives the second order response
function as
G
(2)
(k, t
12
) =
1
2
dt
e
−
0
k
2
(k
2
+m
2
)(t
1
−t
)
p
1
+p
2
=
k
(p
2
1
−p
2
2
)(p
2
2
−k
2
)
×
dt
dt
e
−
0
p
2
1
(p
2
1
+m
2
)(t
−t
)
2
0
k
2
e
−
0
k
2
(k
2
+m
2
)(t
−t
2
)
2
0
p
2
2
× e
−
0
p
2
2
(p
2
2
+m
2
)(t
+t
−2t
)
+ an identical term with p
1
↔p
2
=
0
k
2
p
1
+p
2
=
k
dt
e
−
0
k
2
(k
2
+m
2
)(t
1
−t
)
(p
2
1
−p
2
2
)(p
2
2
−k
2
)
p
2
2
+m
2
× dt
e
−[
0
p
2
1
(p
2
1
+m
2
)+
0
p
2
2
(p
2
2
+m
2
)](t
−t
)
e
−
0
k
2
(k
2
+m
2
)(t
−t
2
)
+ an identical term with p
1
↔p
2
=−
0
k
2
dt
dt
p
1
+p
2
=
k
(p
2
1
−p
2
2
)
2
(k
2
+m
2
)
(p
2
1
+m
2
)(p
2
2
+m
2
)
× e
−
0
k
2
(k
2
+m
2
)(t
1
−t
)
×e
−[
0
p
2
1
(p
2
1
+m
2
)+
0
p
2
2
(p
2
2
+m
2
)](t
−t
)
× e
−
0
k
2
(k
2
+m
2
)(t
−t
2
)
(4.2.10)
In Fourier space
G
(2)
(k, ω) =
∞
−∞
G
(2)
(k, t
12
)e
iωt
12
dt
12
=−
0
k
2
(k
2
+m
2
)
[−iω +
0
k
2
(k
2
+m
2
)]
2
×
d
D
p
(2π)
D
[p
2
−(
k −p)
2
]
2
(p
2
+m
2
)[(
k −p)
2
+m
2
]
×
1
[−iω +
0
p
2
(p
2
+m
2
) +
0
(
k −p)
2
{(
k −p)
2
+m
2
}]
=−G
0
˜
(k, m, ω) G
0
(4.2.11)
where
˜
(k, m, ω) =
(k
2
+m
2
)
0
k
2
p
1
+p
2
=
k
d
D
p
1
(2π)
D
[p
2
1
−p
2
2
]
2
(p
2
1
+m
2
)(p
2
2
+m
2
)
×
1
−iω +
0
p
2
1
(p
2
1
+m
2
) +
0
p
2
2
(p
2
2
+m
2
)
(4.2.12)
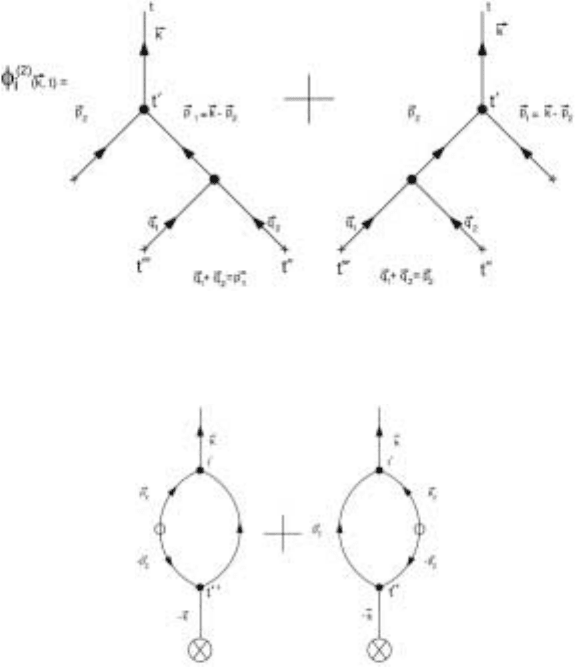
90 4 Mode Coupling Theories
The series for G(k, ω) is thus given by
G(k, ω) =G
(0)
(k, ω) −g
2
G
0
˜
G
0
+O(g
4
)
The diagrammatic representation for the response function can be found from
Fig. 4.2 by taking the product with N
i
(−k, t
2
) and averaging. The process of
averaging two noise terms brings two time arguments together and one momentum
is the negative of the other. The resulting diagrams are shown in Fig. 4.3,
Figure 4.2. How a field at present is affected by the past
Figure 4.3. The one loop response function
where the line with momentum p carrying the symbol
in the middle has
the static correlation factor (2
0
p
2
) attached to it, while a line of momentum p
carrying the symbol
at the end carries only an additional factor of 2
0
p
2
.Ifwe
imagine working to higher order in the coupling constant in g, then new diagrams
