Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.

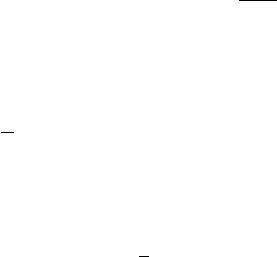
5.3 One-Loop Perturbation Theory 111
perturbation theory for the transport coefficient λ. What we need to calculate is
the lowest order contribution to the self-energy for ψ and v, in terms of which, we
write the response function as,
G
ψ
−1
(k,κ,ω)=G
ψ
(0)−1
+
ψ
(k,κ,ω) (5.3.1)
G
v
−1
(k,κ,ω)=G
v
(0)−1
+
v
(k,κ,ω) (5.3.2)
A practical way of calculating the response function like
G
ψ
=
∂ψ
∂N
ψ
is to calculate the correlation function ψ(k)N
ψ
(−k). If we write Eqns.(5.2.13)
and (5.2.14) in frequency space,
(−iω +
λ
χ
k
2
)ψ(
k, ω)=−i
p,ω
k
j
v
j
(
k −p, ω −ω
)ψ(p, ω
) + N
ψ
(
k, ω)
(5.3.3)
(−iω +νk
2
)v
j
(
k, ω) =
i
2
P
jl
(k)
p,ω
[p
2
+(
k −p)
2
]p
l
ψ(
k −p, ω −ω
)
×ψ(p, ω
) + N
v
j
(
k, ω) (5.3.4)
then the zeroth order solutions (ignores the non-linear terms) are
ψ
(0)
(
k, ω)=G
ψ
(0)
(
k, ω)N
ψ
(
k, ω) (5.3.5)
v
(0)
j
(
k, ω)=G
v
(0)
(
k, ω)N
v
j
(
k, ω) (5.3.6)
If we expand the fields as
ψ(
k, ω)=ψ
(0)
(
k, ω)+ψ
(1)
(
k, ω)+ψ
(2)
(
k, ω)+..... (5.3.7)
v
(0)
j
(
k, ω)=v
(0)
j
(
k, ω)+v
(1)
j
(
k, ω)+v
(2)
j
(
k, ω)+...... (5.3.8)
where ψ
(1)
(
k, ω) and v
(1)
j
(
k, ω) are the first iteration contribution coming from
Eqns.(5.3.3) and (5.3.4). Explicitly,
ψ
(1)
(
k, ω)=−iG
(0)
ψ
(
k, ω)
p,ω
k
j
v
(0)
j
(
k −p, ω −ω
)ψ
(0)
( p, ω
) (5.3.9)

112 5 Critical Dynamics in Fluids
and
v
(1)
j
(
k, ω)=
i
2
P
jl
(k) G
(0)
v
(
k, ω)
p,ω
[−p
2
+(
k −p)
2
]
×p
l
ψ
(0)
(
k −p, ω −ω
)ψ
(0)
( p, ω
) (5.3.10)
(the projection operator P
jl
ensures the incompressibility condition). Going to the
next order
ψ
(2)
(
k, ω)=−iG
(0)
ψ
(
k, ω)
p,ω
k
j
[v
(0)
j
(
k −p, ω −ω
)ψ
(1)
( p, ω
)
+ v
(1)
j
(
k −p, ω −ω
)ψ
(0)
( p, ω
)] (5.3.11)
v
(2)
j
(
k, ω)=
i
2
G
(0)
v
(
k, ω)
p,ω
[(
k −p)
2
−p
2
]p
j
{ψ
(1)
(
k −p, ω −ω
)ψ
(0)
( p, ω
)
+ ψ
(0)
(
k −p, ω −ω
)ψ
(1)
( p, ω
)} (5.3.12)
To construct the response function
G
ψ
(
k, ω)=ψ(
k, ω)N(−
k, −ω)=ψ
(0)
(
k, ω)N(−
k, −ω)
+ψ
(1)
(
k, ω)N(−
k, −ω)
+ψ
(2)
(
k, ω)N(−
k, −ω)+.. (5.3.13)
The first term is our G
(0)
ψ
(k, ω). The second term is zero, when we use Eq.(5.3.9)
and find that v
(0)
j
cannot be paired. The first non-zero contribution has to come
from the third term.
ψ
(1)
N
ψ
=−iG
(0)
ψ
(k, ω)
[v
(0)
j
(
k −p, ω −ω
)ψ
(1)
(p, ω
)
+v
(1)
j
(
k −p, ω −ω
)ψ
(0)
]k
j
N
ψ
(−k, −ω) (5.3.14)
We will handle the two terms separately. First
p,ω
v
(0)
j
(
k −p, ω −ω
)ψ
(1)
(p, ω
)k
j
N
ψ
(−k, −ω)
=−i
p,ω
v
(0)
j
(
k −p, ω −ω
)k
j
G
(0)
ψ
(p, ω
)
×
q,ω
p
l
v
(0)
l
(
k −p, ω
−ω
)ψ
(0)
(q, ω
)N
ψ
(−k, ω)
5.3 One-Loop Perturbation Theory 113
p,ω
v
(0)
j
(
k −p, ω −ω
)ψ
(1)
(p, ω
)k
j
N
ψ
(−k, −ω)
=−i
p,ω
k
j
p
l
q,ω
v
(0)
j
(
k −p, ω −ω
)v
(0)
l
v
(0)
j
( p −q,ω
−ω
)
×G
(0)
ψ
(p, ω
)ψ
(0)
(q, ω
)N
ψ
(−k, −ω)
=−i
p,ω
k
j
p
l
q,ω
C
(0)
v
(
k −p, ω −ω
)P
jl
(
k −p)
×G
(0)
ψ
(p, ω
)G
(0)
ψ
(k, ω) δ(q −
k) δ(ω −ω
)
=−i
p,ω
k
j
p
l
P
jl
(
k −p) C
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
(p, ω
)G
(0)
ψ
(k, ω)
(5.3.15)
where we have used Eq.(5.3.9) for ψ
(1)
(p, ω
) and the fact that in the zeroth order, a
complicated correlation function factors into products of correlations of two fields
at a time, which is Wick’s theorem for problems of this sort. Very often there will
be more than one way of doing the factoring and the final answer is the sum of all
possible factorings. For the second contribution in Eq.(5.3.14)
p,ω
k
j
v
(1)
j
(
k −p, ω −ω
)ψ
(0)
(p, ω
)N(−k, −ω)
= i
p,ω
k
j
G
(0)
v
(
k −p, ω −ω
)P
jl
(
k −p)
q,ω
[κ
2
+(
k −p −q)
2
]q
l
×ψ
(0)
(
k −p −q,ω −ω
−ω
)ψ
(0)
(q, ω
)ψ
(0)
(p, ω
)N(−k, −ω)
= i
p,ω
q,ω
k
j
q
l
P
jl
(
k −p) G
(0)
v
(
k −p, ω −ω
)[κ
2
+(
k −p −q)
2
]
×{ψ
(0)
(
k −p −q,ω −ω
−ω
)ψ
(0)
(p, ω
)ψ
(0)
(q, ω
)N(−k, −ω)
+ψ
(0)
(q, ω
)ψ
(0)
(p, ω
)ψ
(0)
(
k −p −q,ω −ω
−ω
)N(−k, −ω)}
= i
p,ω
q,ω
k
j
q
l
P
jl
(
k −p) G
(0)
v
(
k −p, ω −ω
)[κ
2
+(
k −p −q)
2
]
×{C
(0)
ψ
(p, ω
)G
(0)
ψ
(k, ω)δ(q −
k) δ(ω −ω
)
+C
(0)
ψ
(p, ω
)G
(0)
ψ
(k,ω)δ(q +p) δ(ω
+ω
)}
= i
p,ω
k
j
k
l
P
jl
(
k −p) G
(0)
v
(
k −p, ω −ω
)(p
2
+κ
2
)C
(0)
ψ
(p, ω
)G
(0)
ψ
(k, ω)
+i
p,ω
(−k
j
p
l
)P
jl
(
k −p) G
(0)
v
(
k −p, ω −ω
)
×(k
2
+κ
2
)C
(0)
ψ
(p, ω
)G
(0)
ψ
(k, ω)
(5.3.16)

114 5 Critical Dynamics in Fluids
We now use the FDT to write
C
(0)
ψ
(k, ω) =
1
k
2
+κ
2
[G
(0)
ψ
+G
(0)∗
ψ
]
C
(0)
v
= G
(0)
v
+G
(0)∗
v
(5.3.17)
The following identities are used to simplify the various expressions
k
j
p
l
P
jl
(
k −p) = k
j
p
l
δ
jl
−
(
k −p)
j
(
k −p)
l
(
k −p)
2
=
k. p −
(k
2
−
k. p)(
k. p −p
2
)
(
k −p)
2
=
(
k. p)[k
2
+p
2
−2(
k. p)]−(p
2
+k
2
)(
k. p) +p
2
k
2
+(
k. p)
2
(
k −p)
2
=
p
2
k
2
−(
k. p)
2
(
k −p)
2
(5.3.18)
k
j
k
l
P
jl
(
k −p) = k
2
−
(k
2
−
k. p)
2
(
k −p)
2
=
p
2
k
2
−(
k. p)
2
(
k −p)
2
(5.3.19)
We now put together Eqns.(5.3.14), (5.3.15) and (5.3.16) to write
ψ
(2)
N
ψ
=−G
(0)
ψ
(k, ω)
d
D
p
(2π)
D
dω
2π
p
2
k
2
−(
k. p)
2
(
k −p)
2
C
(0)
v
(k −p, ω −ω
)
×G
(0)
ψ
(p, ω
) +
p
2
k
2
−(
k. p)
2
(
k −p)
2
G
(0)
v
(
k −p, ω −ω
)C
(0)
ψ
(p, ω
)
×(k
2
+κ
2
) −
p
2
k
2
−(
k. p)
2
(
k −p)
2
G
(0)
v
(
k −p, ω −ω
)
×C
(0)
ψ
(p, ω
)(p
2
+κ
2
)
G
(0)
ψ
(k, ω) (5.3.20)
We now make use of the FDT. This expresses the correlation function in terms
of the response functions as shown in Eq.(5.3.17). The response function has the
advantage that it is causal and so in the frequency space all the poles in G(k, ω)
have to occur in the lower half plane. Consequently, we have the frequency integral
C
(0)
v
(
k −p, ω −ω
)G
ψ
( p, ω
)dω
=
dω
G
(0)
v
(
k −p, ω −ω
)
+G
(0)∗
v
(
k −p, ω −ω
)
G
(0)
ψ
( p, ω
)
=
G
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
( p, ω
)dω
(5.3.21)

5.3 One-Loop Perturbation Theory 115
The last step follows from the fact that G
(0)
ψ
has poles only in the lower half of the
complex ω
-plane. Similarly, G
(0)
v
(ω −ω
) has poles only in the lower half of the
complex ω −ω
plane and hence in the upper half of the complex ω
-plane. This
puts the ω
-poles of G
(0)∗
v
(ω −ω
) in the lower half of the complex ω
-plane. Since
G
(0)∗
v
(ω −ω
) and G
ψ
(ω
) have no poles in the upper half plane the integral
G
(0)∗
v
(ω −ω
)G
(0)
ψ
(ω
)dω
=0.
In each of the three terms on the R.H.S of Eq.(5.3.20) an identical argument when
carried through gives
ψ
(2)
N
ψ
=−[G
(0)
ψ
(k, ω)]
2
d
D
p
(2π)
D
dω
2π
p
2
k
2
−(
k. p)
2
(
k −p)
2
×
k
2
+κ
2
p
2
+κ
2
G
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
(p, ω
) (5.3.22)
Noting that
(
k −p)
2
−[(
k −p).
k]
2
= k
4
+p
2
k
2
−2k
2
(
k. p) −[k
2
−p.
k]
2
= p
2
k
2
−( p.
k)
2
We can now cast Eq.(5.3.22) in the form
ψ
(2)
N
ψ
=−[G
(0)
ψ
(
k, ω)]
2
d
D
p
(2π)
D
dω
2π
k
2
+κ
2
p
2
+κ
2
×k
2
sin
2
θG
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
( p, ω
)
=−k
2
(k
2
+κ
2
)[G
(0)
ψ
(
k, ω)]
2
d
D
p
(2π)
D
dω
2π
sin
2
θ
p
2
+κ
2
×G
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
( p, ω
) (5.3.23)
where θ is the angle between
k and q =
k −p. From the contribution to the response
function in the second order perturbation as shown in Eq.(5.3.23), the self-energy
ψ
is (as should be clear from our discussion in Chapter 2),
ψ
(k,κ,ω) = k
2
(k
2
+κ
2
)
d
D
p
(2π)
D
dω
2π
sin
2
θ
p
2
+κ
2
×G
(0)
v
(
k −p, ω −ω
)G
(0)
ψ
( p, ω
) (5.3.24)
We now turn to the velocity response and write
v
j
(
k, ω)N
(v)
j
(−
k, −ω)=v
(0)
j
N
(v)
j
+v
(1)
j
N
(v)
j
+v
(2)
j
N
(v)
j
+......
= G
(0)
(
k, ω)(D −1) +v
(1)
j
N
(v)
j
+v
(2)
j
N
(v)
j
+.......
(5.3.25)

116 5 Critical Dynamics in Fluids
The factor D −1 comes from the sum over j in the projection operator in a
D-dimensional space. With v
(1)
j
from Eq.(5.3.10), we find easily that
v
(1)
j
N
(1)
j
=0.
The first nontrivial contribution comes from the third term in Eq.(5.3.25). Using
Eq.(5.3.12)
v
(2)
j
N
(v)
j
=
i
2
G
(0)
v
(
k, ω)P
jl
(
k)
p,ω
[(
k −p)
2
−p
2
]p
l
ψ
(0)
( p, ω
)
×ψ
(1)
(
k −p, ω −ω
) +ψ
(0)
(
k −p, ω −ω
)ψ
(1)
( p, ω
)
×N
v
j
(
k, ω)
=
1
2
G
(0)
v
(
k, ω)P
jl
(
k)
p,ω
[(
k −p)
2
−p
2
]p
l
q,ω
(
k −p)
n
×G
(0)
ψ
(
k −p, ω −ω
)ψ
(0)
(q,ω
)v
(0)
n
(
k −p −q,ω −ω
−ω
)
×ψ
(0)
( p, ω
) + p
n
G
(0)
ψ
( p, ω
)ψ
(0)
(q,ω
)v
(0)
n
( p −q,ω
−ω
)
×ψ
(0)
(
k −p, ω −ω
)
=
1
2
G
(0)
v
(
k, ω)P
jl
(
k)
ω
,ω
p,q
[( p −
k)
2
−p
2
]
p
l
(
k −p)
n
×G
(0)
ψ
(
k −p, ω −ω
) v
(0)
n
(
k −p −q,ω −ω
−ω
)N
v
j
(
k, ω)
×ψ
(0)
(q,ω
)ψ
(0)
( p, ω
)+p
l
p
n
G
(0)
ψ
( p, ω
)ψ
(0)
(q,ω
)
×ψ
(0)
(
k −p, ω −ω
)v
(0)
n
( p −q,ω
−ω
)N
(v)
j
(
k, ω)
=
1
2
G
(0)
v
(
k, ω)P
jl
(
k)
p,ω
[( p −
k)
2
−p
2
]
p
l
(
k −p)
n
C
(0)
ψ
(p, ω
)
×G
(0)
ψ
(
k −p, ω −ω
)G
(0)
v
(
k, ω)P
nj
(
k) + p
l
p
n
G
(0)
ψ
(p, ω
)
×C
(0)
ψ
(
k −p, ω −ω
)G
(0)
v
(
k, ω)P
nj
(
k)
(5.3.26)
We now use the FDT and the identities
P
jl
(k) p
l
(
k −p)
n
P
nj
(k) =−P
jl
(k) p
l
p
n
P
nj
(k) =−p
2
+( p.
k)
2
/k
2
,

5.4 Diagrammatic Perturbation Theory 117
to simplify Eq.(5.3.26) and write it as
v
(2)
j
N
(v)
j
=−
1
2
[G
(0)
v
(k, ω)]
2
d
D
p
(2π)
D
dω
2π
G
(0)
ψ
(p, ω
)G
(0)
ψ
(k −p, ω −ω
)
×
[p
2
−(
k −p)
2
]
2
[p
2
−
( p.
k)
2
k
2
]
(p
2
+κ
2
)[κ
2
+( p −
k)
2
]
(5.3.27)
Comparing with Eq.(5.3.25) and remembering the construction of the self energy
from the perturbation series for G, we have for the second order perturbation theory
v
=
1
2(D −1)
d
D
p
(2π)
D
dω
2π
G
(0)
ψ
(p, ω
)G
(0)
ψ
(k −p, ω −ω
)
×
p
2
sin
2
θ [p
2
−(
k −p)
2
]
2
(p
2
+κ
2
)[κ
2
+( p −
k)
2
]
(5.3.28)
In Eqns.(5.3.24) and (5.3.28), we have constructed the lowest order (second order
in perturbation theory) self energies for the order parameter and velocity fields.
These are the contributions to the relaxation rate for these and we will analyse
them in what follows to see what they imply for the contribution of the critical
fluctuations.
Figure 5.1. Vertex for the order parameter fluctuations
5.4 Diagrammatic Perturbation Theory
In this section, we show the perturbation theory in diagrammatic terms. We have
two kinds of fields - straight lines which denote the order parameter field and wavy
lines which denote the velocity field. There are two kinds of vertices shown in
Figs. 5.1a and 5.1b
118 5 Critical Dynamics in Fluids
Figure 5.1. Vertex for the velocity fluctuations
i) the order parameter line breaking into a order parameter and a velocity field
ii) the velocity line breaking into two order parameter lines
The momentum factors occurring with the vertices are shown in the figure. At
each vertex, momentum and frequency are conserved. We now make the convention
that a line with an arrow is a propagator and a line with a circle is a correlator. The
noise for the concentration field is shown by a dot within the circle and that for
the velocity field is shown by a cross within a circle. The response function being
a correlation of the field and noise, the diagrammatic representation is shown in
Fig. 5.2
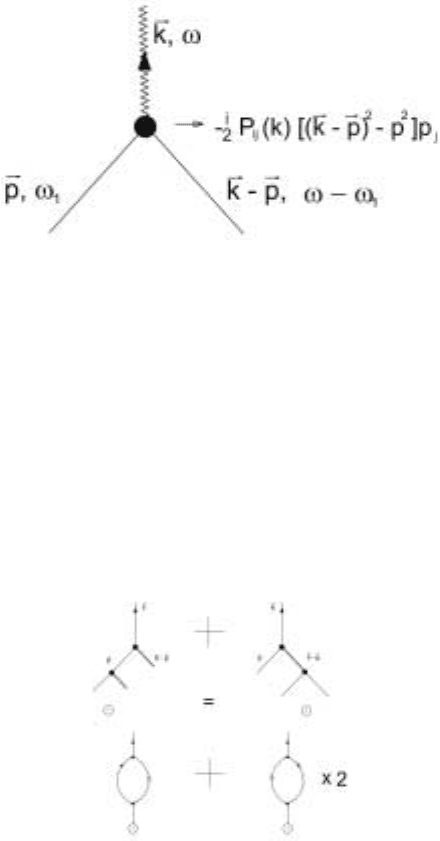
Figure 5.2. Order parameter response function at one loop order
The factor of 2 shown in one of the diagrams is = in? Fig. 5.2a comes from
the combinatorics - either of the two lines emanating from the velocity line at
momentum
k −p can combine with the noise term. Reading off the contribution
from Fig. 5.2a according to the rules, we have the second order contribution G
(2)
ψ
to G
ψ
work out as

5.4 Diagrammatic Perturbation Theory 119
Figure 5.2. Velocity response function at one loop order
G
(2)
ψ
=[G
(0)
ψ
]
2
p,ω
{(−ik
j
)(−ip
l
)P
jl
(k −p)G
(0)
ψ
(p, ω
)
×C
(0)
(k −p, ω −ω
) +2 ×(−ik
j
)
i
2
P
jl
(k −p)p
l
[k
2
−p
2
]
×C
(0)
ψ
(p, ω
)G
(0)
v
(k −p, ω −ω
) (5.4.1)
The reader should verify that this is exactly the same as obtained in Eq.(5.3.23).
The contribution G
(2)
v
from Fig. 5.2b can be similarly worked out. If we now go to
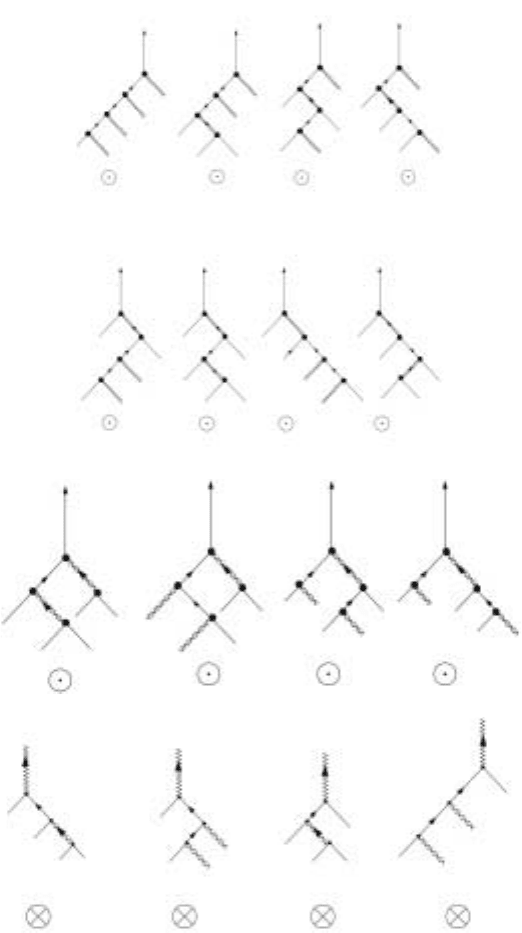
the next two orders then the proliferations are shown in Fig. 5.3 and (5.4).
Figure 5.3. Tracing back the order parameter field to the noise to find the response
With the graphs shown in Figs. 5.3 and 5.4, we now try to form correlation
functions. The graph of Fig. 5.3a gives zero because there is always an uncorrelated
velocity field left. The non-zero contribution comes from Fig. 5.3b. After forming
correlators, the resulting diagrams are shown in Fig. 5.5.
The diagrams in the first row of Fig. 5.5 dress the external G
ψ
(k). The
diagrams in the second row of Fig. 5.5 are self energy insertions - so called
because they consist of dressing the order parameter and velocity lines in the loop
of the second order diagrams shown in Fig. 5.2. These diagrams can in principle
120 5 Critical Dynamics in Fluids
Figure 5.4. Tracing back the velocity field to the noise to find the response function (two
loops)
