Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

5.6 Sound Propagation 131

sin

απ

2zν

cos

απ

2zν

α/zν

(5.6.22)

The attenuation per wavelength α

at T =T

= k

λ =2π

πsin

απ

2zν

cos

απ

2zν

α/zν



α/zν

1 +

α/zν

(5.6.23)

the last line following because the speciﬁc heat exponent α is small i.e. α 1. As

we have seen in the previous section for the liquid-vapour systems z 3inD =3,

ν 2/3 for α 1 and thus

απ

1 +

α/zν

(5.6.24)

For low frequencies, the critical attenuation per wavelength attain the universal

value απ

/4 0.29. For T =T

, the speciﬁc heat is a function of ξ and ω, and is

given by the scaling function

(ξ, ω) =Aξ

α/ν

f (ωξ

) +B (5.6.25)

where f(0) =1 and for x 1, f(x)∝(−ix)

−α/zν

. In the intermediate range the

function f(x)needs to be calculated from a complete theory of frequency depen-

dent speciﬁc heat.

Returning to the binary liquid, the order parameter is not directly connected

to the sound propagation. Consequently, the velocity does not show the critical

behaviour of Eq.(5.6.16) near the consolute point. Instead, near the consolute point

the isentropic derivative

∂P

∂ρ



can be written as

∂P

∂ρ



(5.6.26)

- the proof of which is being left to one of the problems. The constant C

is of

the order of a few hundreds of metres and the additional part which has a strong

temperature dependence due to critical ﬂuctuations is about one percent change

on this large background. The constant pressure speciﬁc heat for the consolute

point has the structure shown in Eq.(5.6.25). For a binary liquid the background

contribution B dominates the critical part, and linearizing in this part, we can write

Eq.(5.6.26) in the form,

−

α/ν

f(ωξ

) (5.6.27)

132 5 Critical Dynamics in Fluids

and thus from Eq.(5.6.18), the attenuation per wavelength is given by

=2π



πC

α/ν

Im f(ωξ

) (5.6.28)

At the critical point, the attenuation

= Im

πC

(−iω)

−α/zν

πC

−α/zν

(5.6.29)

where A

is a constant. The ratio

/α

=G() (5.6.30)

is a function of the scaled variable  =ωξ

, which is an important prediction

of these considerations. We have experimental evidence of this in the last section.

The actual calculation of G() requires the theory of frequency dependent speciﬁc

heat.

5.7 The Lambda Transition

This is where dynamic scaling began. At 2.172

K, liquid He

undergoes a second

order phase transition to a state characterized by inﬁnite thermal conductivity. It

also has a very low shear viscosity (it is only the rotation viscometer which picks up

the viscosity, the liquid ﬂows without apparent viscosity) which decreases strongly

as the temperature decreases. This new phase of the liquid is called the superﬂuid

and the transition is from a normal to a superﬂuid state. The speciﬁc heat diverges

almost at the transition temperature and its temperature dependence resembles the

Greek letter λ, which gives the transition its name. The order parameter of the

transition is a mesoscopic quantum wavefunction for the ground state. This has

a magnitude and a phase and this is a complex number. In the Ginzburg-Landau

parlance it is a two component order parameter and the static properties of the

transition are well understood in terms of the Ginzburg-Landau free energy.

In order to set up the equation of motion for the dynamics of the superﬂuid we

need to worry about the conservation laws with the different densities. For conser-

vation laws we need currents and for the superﬂuid phase there is a special current

which is quantum mechanical in nature. A quantum mechanical wavefunction ψ

is associated with a current which we call the supercurrent



and we write in the

usual fashion





Im (ψ

∗



∇ψ) (5.7.1)

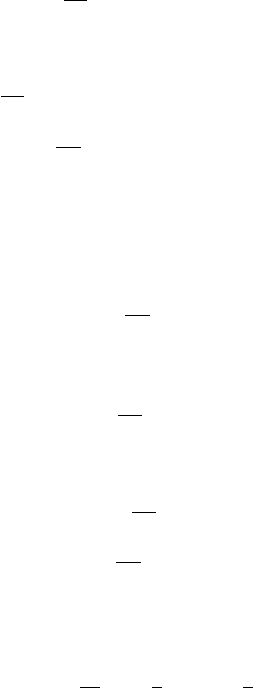
5.7 The Lambda Transition 133

With ψ =|ψ|e

iφ

, we can see that the superﬂuid velocity v

is given by the gradient

of the phase

v



∇φ (5.7.2)

The normal ﬂuid carries the entropy and the normal current



=ρ

v

, where v

is the normal ﬂuid velocity and ρ

is the normal ﬂuid density. The total current is



j =



. The total density ρ =ρ

+ρ

is not the critical mode and to the ﬁrst

approximation we can ignore the ﬂuctuations in the total density. This implies no

total current in the system so that



j =0. Entropy ﬂuctuations are associated with

the normal ﬂuid and hence they will be sensitive to the critical ﬂuctuations. If we

write S as the entropy density, the entropy current is σ



where σ is the entropy

per unit mass then the conservation law for entropy takes the form

∂S

∂t

+σ



∇.



=0 (5.7.3)

With no total current in the system

∂S

∂t

=−σ



∇.



=σ



∇.



σ 

(ψ

∇

−ψ

∇

) (5.7.4)

where ψ =ψ

+iψ

Now, the gradient of the chemical potential µ drives the superﬂuid current and

the acceleration equals the gradient of µ. The chemical potential ﬂuctuation is

induced by the entropy ﬂuctuations and this leads to the equation of motion

φ =

σ 

S. (5.7.5)

Noting that ψ =|ψ|e

iφ

and thus

ψ =iψ

φ,wehave

ψ =

σ 

iψS (5.7.6)

Writing in terms of the components

=−

σ 

S (5.7.7)

The Ginzburg-Landau free energy which describes the equilibrium ﬂuctuations is

given by

F =



(



∇ψ)

] (5.7.8)

134 5 Critical Dynamics in Fluids

where we have ignored the quartic term in the free energy and included its effect in

the statics through the phenomenological procedure of using a renormalized mass

κ which vanishes at the critical point with the correct correlation length exponent

ν. We have made another drastic assumption. The equilibrium correlation of the

entropy ﬁeld is a constant according to the free energy functional of Eq.(5.7.8).

However, the entropy correlation is supposed to be the constant pressure speciﬁc

heat. In reality the speciﬁc heat has a weak (logarithmic) divergence at the lambda

point. The effect of this will be lost in the dynamics when we use Eq.(5.7.). How-

ever, this is an extremely small effect. The nonlinear terms that we have used in

Eqns(5.7.) and (5.7.) conserve the free energy of Eq.(5.7.8) as the reversible terms

should. To complete the equations for ψ and S we now need to introduce the dis-

sipative part as the functional derivative of of F and the noise term that will ensure

the existence of the equilibrium distribution function. It should be noted that there

is no conservation law associated with the order parameter, but the entropy is a

conserved variable. We thus have the dynamics prescribed by

=−g

S −(κ

−∇

)ψ

(5.7.9)

= g

S −(κ

−∇

)ψ

(5.7.10)

S = g

(ψ

∇

−ψ

∇

) +λ∇

S +N

(5.7.11)

where g

σ 

and

N

(x

)=2δ

(x

−x

)δ(t

−t

)δ

N

(x

)=2δ

(x

−x

)δ(t

−t

)δ

(5.7.12)

In momentum space, the equations are

=−g



p

S(p)ψ

(k −p) −(k

+κ

)ψ

(k) +N

(k) (5.7.13)

= g



p

S(p)ψ

(k −p) −(k

+κ

)ψ

(k) +N

(k) (5.7.14)

S(k) = g



p

+p



−p

)ψ

) −λk

S(k)+N

(k) (5.7.15)

with the appropriate noise correlations. Let us use these equations ﬁrst for T<T

without the dissipative and stochastic terms. The situation for T<T

, is charac-

terized by the existence of a non zero expectation value of the order parameter

ﬁeld. Suppose this symmetry breaking occurs in ψ

and ψ

=m

=0. We write

, where m

is independent of time and space. In Fourier space, m

has only a k =0 component and we can write Eqns.(5.7.10) and (5.7.11), linearized

in ψ

andSas

(k) = g

S(k) (5.7.16)

and

S(k) =−g

(k) (5.7.17)

5.7 The Lambda Transition 135

This leads to the oscillations

= 0 (5.7.18)

S +g

S = 0 (5.7.19)

The temperature ﬂuctuations and the transverse ﬂuctuations of the order parameter

ﬁeld (the Goldstone mode) propagate with frequency

ω =g

k (5.7.20)

This is the second sound in superﬂuid Helium - it corresponds to the entropy and

hence temperature ﬂuctuations. The order parameter expectation value has the

critical behaviour m ∼κ

β/ν

. Ignoring the small anomalous dimension exponent η,

α +2β +2ν =2,

which combined with the Josephson relation

Dν =2 −α,

leads to

−1.

From Eq.(5.7.20)

ω ∝kκ

β/ν

=kκ

D/2−1

(5.7.21)

We now imagine approaching the lambda point with the wavenumber kept ﬁnite.

The correlation length increases and once κ k, the frequency does not respond

any more and hence at T =T

(i.e.κ =0)

ω ∝k

D/2

(5.7.22)

Thus, z =D/2 for the superﬂuid transition and it is the same for the order parameter

and entropy ﬁelds. The argument, that we have just given is the dynamic scaling

argument. The basic assumption that there is only one characteristic time in the

system and it is a homogeneous function of k and κ, i.e.

ω =k





(5.7.23)

The function f will be different for ψ and S but z is the same.

If we now include the dissipation then frequency is complex and can be written

ω =ω

+iDk

(5.7.24)

136 5 Critical Dynamics in Fluids

where D is the damping coefﬁcient. For κ k, ω

∝k

D/2

according to Eq.(5.7.22)

and if there is only one frequency scale then Dk

must behave as k

D/2

and hence

D(k) ∝k

D/2−2

for κ k. Dynamic scaling hypothesis now asserts that

D(k, κ) =k

−2

D(k/κ) (5.7.25)

and for κ k

D(κ) ∝κ

D/2−2

=ξ

2−D/2

=ξ

/2

(5.7.26)

Thus the damping diverges as the correlation length becomes inﬁnite.

If we now go through the transition to the normal phase, then the second sound

mode disappears and becomes a diffusive mode - the diffusion corresponding to the

thermal conductivity. The continuity of the entropy mode ensures that the thermal

conductivity diverges as ξ

/2

due to superﬂuid ﬂuctuations in the normal state near

the transition point. The deﬁnite predictions for D =3, are

Thermal conductivity λ ∝ t

−1/3

(T > T

)

Second sound damping D ∝ t

−1/3

(T < T

)

The thermal conductivity measurement is extremely precise. It showed a clear cut

divergence, but the exponent appeared about 20% higher. The resolution of this

problem was an interesting tour de force. We will provide some feeling for the

issues involved in the next section.

5.8 Generalized n-Vector Model

In this section, we introduce a slightly generalized model which will help us make

a qualitative point very easily. We introduce a n-component vector order parameter

ﬁeld



ψ(ψ

,ψ

.....ψ

), and a n(n −1)/2 component antisymmetric tensor entropy

ﬁeld S

with the equation of motion

(k) =−g



p

( p)ψ

(



k −p) −(k

+κ

)ψ

(k) +N

(k) (5.8.1)



p

+p



−p

)ψ

(p −2) −λk

(k) +N

(k) (5.8.2)

There is no cross correlation either between the noise for the order parameter and

entropy ﬁelds or between the different components of noise for the same ﬁeld. For

n =2, we get back the equations of motion for the superﬂuid transition as written

down in Eqns.(5.7.13), (5.7.14) and (5.7.15).

Our task now is to construct the relaxation rates for the order parameter and

entropy ﬁelds. At the zeroth order (i.e. dropping the nonlinear terms)

5.8 Generalized n-Vector Model 137

(0)

]

−1

=−iω +(k

+κ

) (5.8.3)

(0)

]

−1

=−iω +λk

(5.8.4)

(0)

2

+

+κ2)

+κ

(0)

∗

] (5.8.5)

(0)

2λk

+λ

(0)

∗

(5.8.6)

To ﬁnd the contribution from the nonlinear terms we need to calculate the self

energies of ψ and S ﬁelds. The self energies can be constructed from the elements

shown in Fig. 5.7. The entropy line is wavy and the order parameter line is straight.

The order parameter noise is a circle with a dot and the entropy noise is a circle

with a cross. Translating the diagrammatics to algebraic expressions,

(2)

(k) ={G

(0)

(k, ω)}



(2π)

dω



2π

(−g

)[G

(0)

(k −p, ω −ω



)

×C

(0)

(p, ω



) +{k

−(



k −p)

(0)

(p, ω



(0)

(k −p, ω −ω



)]

=−g

(0)

(k, ω)}



(2π)

dω



2π

(0)

(k −p, ω −ω



)

×G

(0)

(p, ω



)

+κ



k −p)

(5.8.7)

and

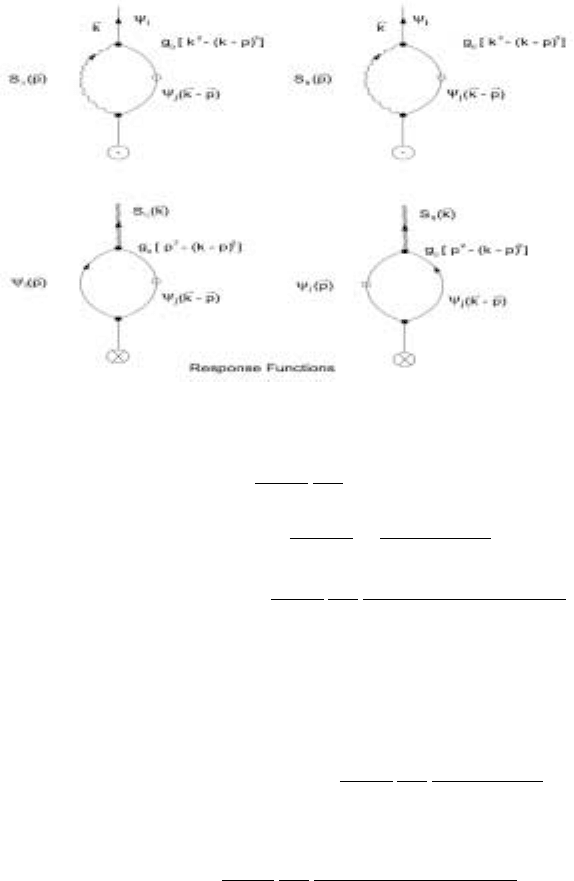
138 5 Critical Dynamics in Fluids

Figure 5.7. Order parameter and entropy response functions for the superﬂuid transition

(2)

(k) ={G

(0)

(k, ω)}



(2π)

dω



2π

−(



k −p)

(0)

(p, ω



)

×G

(0)

(k −p, ω −ω



)



+κ

−



k −p)



=−{G

(0)

(k, ω)}



(2π)

dω



2π

−(



k −p)

]

+κ

)[κ

+( p −



]

×G

(0)

(p, ω



(0)

(k −p, ω −ω



) (5.8.8)

For the ψ

there will be (n −1) diagrams of the kind shown if Fig. 5.7b and hence

there will be a factor of (n −1) multiplying G

(2)

. The self energies are



(k,κ,ω) = g

+κ

)(n −1)



(2π)

dω



2π



k −p)

×G

(0)

(k −p, ω −ω



(0)

(p, ω



) (5.8.9)



(k,κ,ω) =−g



(2π)

dω



2π

−(



k −p)

]

+κ

)[κ

+( p −



]

×G

(0)

(p, ω



(0)

(k −p, ω −ω



) (5.8.10)

A self consistent approximation replaces G

(0)

and G

(0)

with G

and G

and

assuming that 

and 

dominate the bare relaxation rate γ(k

+κ

) and λk

we have the following

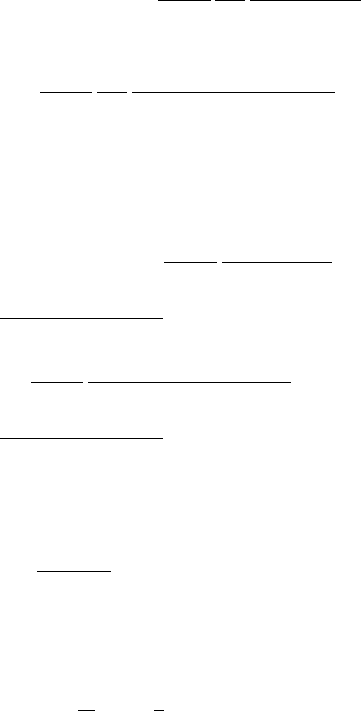
5.8 Generalized n-Vector Model 139

−1

=−iω +

(k,κ,ω) (5.8.11)

−1

=−iω +

(k,κ,ω) (5.8.12)

where



(k,κ,ω) = g

+κ

)(n −1)



(2π)

dω



2π



k −p)

×G

(k −p, ω −ω



(p, ω



) (5.8.13)



(k,κ,ω) =−g



(2π)

dω



2π

−(



k −p)

]

+κ

)[κ

+( p −



]

×G

(p, ω



(k −p, ω −ω



) (5.8.14)

Using Lorentzian approximations for G

and G

to do the frequency integration

in Eqns.(5.8.13) and (5.8.14)



(k, κ) = g

+κ

)(n −1)



(2π)



k −p)



(p) +

(



k −p)

(5.8.15)



(k, κ) = g



(2π)

−(



k −p)]

[κ



k −p)

](p

+κ

)



(p) +

(



k −p)

(5.8.16)

We now make the dynamic scaling Ansatz for the Onsager coefﬁcients 

and λ

which are deﬁned as





(k, κ)

+κ

f(k/κ) (5.8.17)

= 

(k, κ)/k

g(k/κ) (5.8.18)

Power counting of Eqns.(5.8.15) and (5.8.16) conﬁrm that

x =

−2 =



For >0 i.e. D<4, the Onsager coefﬁcients in the long wavelength limit diverges

and the nonlinear contribution to the Onsager coefﬁcients dominate the background

contribution. Our calculations have thus conﬁrmed the dynamic scaling expecta-

tions of §(5.7).

We now want to look at the scaling behaviour of Eqns.(5.8.17) and (5.8.18) a

little more closely. Focussing on the critical point (i.e. κ =0) relaxation, we have

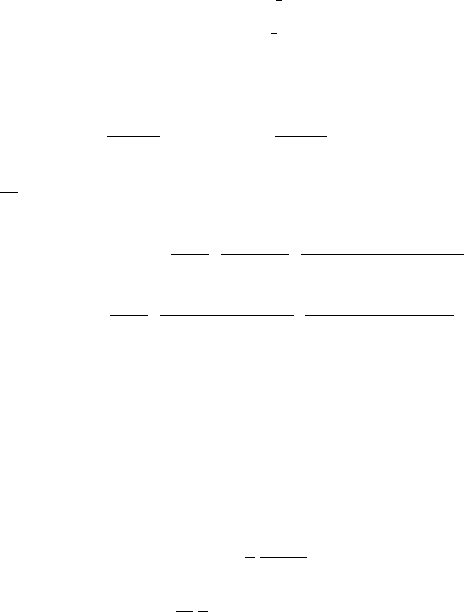
140 5 Critical Dynamics in Fluids



= a

−



(5.8.19)

= a

−



(5.8.20)

where a

and a

are ﬁnite constants. From Eqns(5.8.15) and (5.8.16)

(2π)

I(w,)=

(2π)

J(w,) (5.8.21)

where w =

and

I(w,) = (n −1)



(



1 −p)

D/2



1 −p|

D/2

(5.8.22)

J(w,) =



[(



1 −p)

−p

]

(



1 −p)

D/2



1 −p|

D/2

(5.8.23)

We can ﬁnd the value of w from

I(w,)=J(w,) (5.8.24)

We note that I and J have logarithmic divergences at D =4 and hence as a function

of  =4 −D, there will be poles at  =0, which we can evaluate from the region

p ≥1. Clearly,

I(w,) = (n −1)





1 +w

+0(1)



(5.8.25)

J(w,) =



+0(1) (5.8.26)

To the lowest order in , we ﬁnd that

w =2n −3. (5.8.27)

The important thing with the above result is that for n =3/2, w =0 and hence the

dynamic scaling Ansatz does not work. This is true very close to D =4. At D =3,

a different value of n may be obtained and indeed a two loop calculation shows

that at D =3, n 2, the relevant value of n for the superﬂuid transition. The ratio

w is consequently very small for for the lambda transition. This is not a violation

of dynamic scaling but can have signiﬁcant observational consequences as we will

see.

The dynamic scaling relations shown in Eqns.(5.7.25) and (5.7.26) are valid in

the long wavelength limit i.e. as k →0. If one is concerned with larger values of

k, then there will be corrections to the scaling forms. This is expressed as



= a

−/2

[1 +b

+.......] (5.8.28)

= a

−/2

[1 +b

+.........] (5.8.29)