Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

162 6 Systems Far from Equilibrium

and we have η =σ . The quantity 1/R in Eq.(6.3.24) is the curvature of the spherical

surface and hence Eq.(6.3.24) reads

v =−K (6.3.28)

where v is the wall velocity and K is the curvature multiplied by (D −1). Although

we have derived it for spherical surfaces, this is a general result for any curved

surface - as was ﬁrst established by Allen and Cahn.

For the conserved order parameter it is difﬁcult to consider interfaces indepen-

dently because there is actual diffusion of order parameter from interfaces of high

curvature to regions of low curvature through the intervening bulk phase. To begin

with let us consider the ﬁeld φ inside a bulk phase and write φ =1 +

φ where

φ is

a small deviation from the bulk value. Linearizing in Eq.(6.3.8) in

∂

∂t

=−∇

φ +V



(1)∇

φ (6.3.29)

For large length scales ∇

φ is negligible and

φ satisﬁes a diffusion equation with



(1) as the diffusion coefﬁcient. One can make a further simpliﬁcation. Due to the

conservation law, the interface moves only slightly during the period over which

the diffusive ﬁeld

φ relaxes. If the domain size is L, then the diffusive ﬁeld relaxes

over a time scale L

. A typical surface velocity is L

−2

and hence in that time scale

the interface moves a distance of order unity, which is much less than L. Thus

the relaxation of the diffusion ﬁeld is fast and it can be taken to be in equilibrium

which means

φ satisﬁes ∇

φ =0 in the bulk.

To ﬁnd the boundary condition at the interface, we introduce the chemical

potential µ =

δF

δφ

. Eq.(6.3.8) is the continuity equation which can be rewritten as

φ =−



∇.



j (6.3.30)



j =−



∇µ (6.3.31)

µ = V



(φ) −∇

φ (6.3.32)

In the bulk

µ =V



(0)

φ −∇

φ =V



(1)

for the large length scales and hence µ satisﬁes

∇

µ =0 (6.3.33)

If we once again imagine a spherical droplet

µ =V



(φ) −

∂

∂r

−

D −1

∂φ

∂r

6.3 Phase Ordering Kinetics 163

Multiplying by

∂φ

∂r

and integrating across the interface (symmetric V(φ))

µ =−

σ(D−1)

=−

σK

(6.3.34)

where the second step is the general result for all curved surfaces.

Thus, at the interfaces µ is given in terms of the curvatures. Between the

interfaces, µ satisﬁes Laplace’s equation. The motion of an interface is determined

by the current imbalance between what is ﬂowing in and what is ﬂowing out and

integrating Eq.(6.3.30)

vφ = j

out

−j

=−

∂µ

∂n

(6.3.35)

the second step following from Eq.(6.3.31) where n is in the direction of normal

to the surface.

We now apply this to the spherical domain of size R of negative φ (φ =−1)

embedded in a sea of positive φ. The deﬁnition of µ in Eq.(6.3.32) gives µ =0

at r =∞.Forr>R(t)µis to be found from the solution of ∇

µ =0. At r =R,

in D =3, the value of µ is −σ/R and hence the solution for r>Ris µ =−σ/r.

For r<R, the solution r

−1

is not admissible being singular. Hence, µ =constant

inside r =R and has to match the value −σ/R at r =R. Thus

µ =−

for r>R

=−

for r ≤R (6.3.36)

The velocity follows from Eq.(6.3.35) as

=−

∂µ

∂r



R+

R−

=−

Integrating

(t) =R

(0) −

σt (6.3.37)

and the collapse time scales as R

(0) as opposed to R

(0) of the non conserved case.

We now turn to the ‘growth’law for the domain size L, which is a generalization

of the discussion of the isolated spherical domains. For the non conserved order

parameters, if there is a single characteristic length L, which is the content of the

scaling hypothesis, then the wall velocity has to be of the order of

. On the other

hand, the curvature is O(L

−1

) and hence Eq.(6.3.28) gives

∼

L ∼ t

1/2

(6.3.38)

164 6 Systems Far from Equilibrium

Another way of looking at it is via Eq.(6.3.25). A domain of size R collapses in

a time of the order of R

and hence after time t, there will be no domains of size

smaller than t

1/2

, so that the characteristic domain size is L(t) ∼t

1/2

For the conserved order parameter, at the interface the chemical potential is

µ ∼

. It varies over a distance whose characteristic size is L and hence |



∇µ|∼

The current and hence the velocity is proportional to



∇µ and consequently,

∼

or L ∼ (σ t)

1/3

(6.3.39)

We would arrive at a similar result using Eq.(6.3.7) as in the case of the non

conserved order parameter.

6.4 Topological Defects

So far, we have discussed systems with a scalar order parameter and where an ‘up’

phase changed to a ‘down’ phase , we had a domain wall, which can be viewed as

a defect in the topology. Consequently, a domain wall can be called a ‘topological’

defect. In general by a topological defect one means a surface on which the order

parameter vanishes and which separates domains of two equilibrium phases.

The generalized free energy functional, which has O(n) symmetry in the order

parameter space is

F =





(∂



φ∂



φ) +V(



φ)



(6.4.1)

The function V(



φ) depends on the magnitude of



φ alone and has the general shape

as shown in Fig. 6.3 for n =2 For non conserved ﬁeld

∂φ

∂t

=∇

−

∂V

∂φ

(6.4.2)

The topological defects can be generated by studying the stationary situation of

Eq.(6.4.2) with the proper boundary conditions. For the O(n) theory in a D-

dimensional space, the requirement that all n components of



φ vanish at the defect

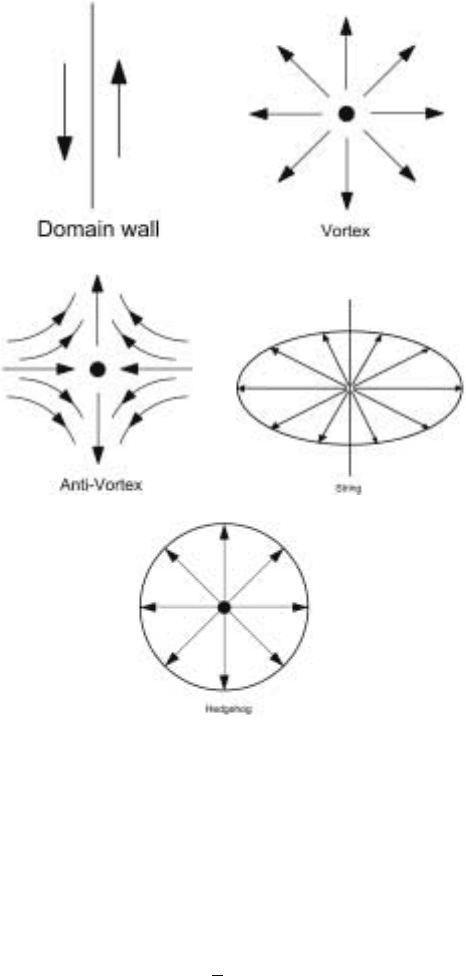
core deﬁnes a surface of dimension D −n. For a defect to exist n ≤D. A domain

wall is a surface of dimension D −1. For n =2, the defects are points in D =2

(vortices) and lines (strings or vortex lines)inD =3. For n =3, in D =3 they are

points (hedgehogs or monopoles). The ﬁelds in the various cases are as shown in

Fig. 6.4

For n<D the ﬁeld



φ varies only in the n dimensions orthogonal to the vortex

core, while remaining stationary in the D −n dimensions parallel to the core. The

coarsening occurs by reduction in radius of curvature which reduces the sharp

6.4 Topological Defects 165

Figure 6.3. A Mexican hat potential

features of the defect. These processes diminish the area of a domain wall or

the length of a vortex line. For point defects, coarsening occurs by the mutual

annihilation of defect-antidefect pairs. An ‘anti-defect’ has a different topological

charge in the direction of the ﬁeld as one goes around the defect.

For the radially symmetric ﬁeld



φ =ˆrf (r) and f(r) is the proﬁle function

which satisﬁes

n −1

−

n −1

f −V



(f ) =0 (6.4.3)

with boundary conditions f(0)=0 and f(∞) =1. The behaviour for large r, can be

obtained by setting f =1 −(r) and linearizing in  to ﬁnd

(r) ≈

n −1



(1)

The approach to saturation is power law like for n>1 as opposed to the exponential

behaviour in Eq.(6.3.17) for n =1.

For this radially symmetric defect the energy per unit core volume is

E =S



drr

n−1



n −1

(



∇f)

+V(f)



(6.4.4)

where S

2π

n/2

(n/2)

is the surface area of a n-dimensional sphere. For n ≥2, the ﬁrst

term in the above expression dominates at large r, since its asymptotic behaviour

is r

−2

. Those of the other two terms are r

−6

and r

−4

. The energy is clearly,

E ∼ln(

sys

) for n =2 and E ∼L

n−2

sys

for n>2.

For a phase ordering system, we have several defects and the ﬁeld of a single

defect will be screened out beyond a characteristic scale L(t) due to the other

defects. So the integration in Eq.(6.4.4) will have to be cut off at L(t ). The dynamics

166 6 Systems Far from Equilibrium

Figure 6.4. Topological singularities in the order parameter ﬁeld

of defect structures much smaller than L(t) are of particular interest since these

are the analogues of the small domains of the scalar system. For D =n =2, these

are the vortex-anti vortex pairs, for D =n =3 these are the monopole-antipole

pairs, for D =3, n =2, these are the vortex rings and so on. Such structures are

characterized by r, the pair separation or the size of the ring. The volume of the

defect core being r

D−n

, the energy of such a structure is

E ∼ r

D−2

D ≥n =2

E ∼ r

D−2

D ≥n>2 (6.4.5)

6.4 Topological Defects 167

The derivative

gives the force which leads to the collapse of the structure.

The force per unit volume is

F(r)∼

⎧

⎪

⎨

⎪

⎩

−

D =n =2

−r

n−3

D>n=2

−r

n−3

D ≥n>2

(6.4.6)

The total energy density  can be calculated by using Eq.(6.4.5) with r =L(t) and

dividing by the value L

, which gives

 =

D ≥n =2

 =

D ≥n>2 (6.4.7)

Let us now look at the dynamics of the defects. For extended defects, the defects

occupy the last D −n dimensions of a cartesian coordinate system deﬁned by

.......x

. Let the velocity of the defect be v in the x

direction. The ﬁeld φ

depends on the coordinates x

..........x

and the rate of change of energy is given



(

i=1

)

δF

δφ

∂φ

∂t

=−



(

i=1

)



∂φ

∂t



(6.4.8)

If the proﬁle is



φ(x

......x

) =



f(x

−vt, x

........x

) (6.4.9)

then

∂



∂t

=−v

∂



∂x

(6.4.10)

and Eq.(6.4.8) becomes

=−v



..........dx



∂



∂x



(6.4.11)

If we make a small velocity approximation then it is permissible to set v =0 in the

integrand in Eq.(6.4.8) and using the equivalence of all n-directions

=−





∇



φ)

=−ηv

(6.4.12)

168 6 Systems Far from Equilibrium

where

η =





∇



φ)

(6.4.13)

which is the energy per unit volume so far as the leading term is concerned (it

is a part of



∇



φ)

which is divergent and dominates the energy - see the

discussion after Eq.(6.)) and diverges with the system size for n ≥2. For small

defect size r, the integral will be cut off at r and we would have a scale dependent

friction coefﬁcient

η(r) ∼ r

n−2

D ≥n =2

∼ r

n−2

D ≥n>2 (6.4.14)

The scaling hypothesis now gives the growth law. From Eq.(6.4.6), the force is

F (L) ∼1/L for D =n =2

or in terms of η

F (L) ∼

η(L) ∼

for D =n =2.

Consequently, for D =n =2,

L ∼



ln t



1/2

(6.4.15)

For all other situations the same argument yields

L ∼t

1/2

(6.4.16)

For the conserved order parameter, this argument would not work - a more general

argument for deriving L(t) would be given later.

The existence of defects has a profound effect on the short term behaviour of

the two point correlation function C(r) =φ(x)φ(x +r). This can be appreciated

from the factthat from the scaling hypothesis ∇φ(r)would be estimated asO(1/L).

Near the defect core, ξ r L, the gradient is much larger since (



∇φ)

∼

.For

the defect ﬁeld to saturate, we need r ξ , while for it to be unaffected by the

other defect ﬁelds, we need r L. Thus short distance is speciﬁed by ξ r L.

Alternatively, large momentum is speciﬁed by

k 

For a scalar ﬁeld, we consider two points x and x +r with ξ r L. The

product φ(x)φ(x +r) will be −1 if a wall passes between them and +1 if there is

no wall . Since r L, we neglect the probability of ﬁnding more than one wall.

To ﬁnd C(r, t), we need to know the probability with which a randomly placed rod

of length r cuts a domain wall. This probability is of the order

and hence

6.5 The Structure Factor 169

C(r,t) ≈(−1)

+1(1 −

) =1 −

(6.4.17)

The correlation function is non-analytic in r at r =0, being linear in |r| (note that

although the above argument breaks down in the core region, we are interested in

the region r ξ, L ξ with

arbitrary, which is to say that the non-analyticity is

in the scaling variable

). Fourier transforming Eq.(6.), we get the structure factor

S(k,t), which has, from dimensional analysis, the form

S(k,t) ∼

D+1

kL 1 (6.4.18)

This is known as Porod’s law. The L-dependence of the result is interesting. The

factor L

−1

is the area of the domain wall per unit volume. For kL 1, the scattering

function (i.e. the structure factor) probes structure on scales much shorter than

typical interwall spacing or radius of curvature. In this regime, the structure factor

scales as the area of the wall since each element of the wall with linear dimension

larger than k

−1

contributes independently to the structure factor.

The above observation allows one to generalize Eq.(6.) to vector ﬁelds. The

idea is that for kL 1, the structure factor should scale as the total volume of the

defect core. Since the dimension of the defect is D −n, the amount of defect per

unit volume scales as L

−n

. This immediately yields

S(k,t) ∼

D+n

kL 1 (6.4.19)

which is a generalized Porod’s law for O(n) ﬁeld.

6.5 The Structure Factor

An extremely important and at the same time difﬁcult issue is the calculation of

the full structure factor S(k, t). In general this can be done exactly only in a few

specialized cases, all of which are somewhat far removed from reality. However,

some of the qualitative features that these somewhat fanciful situations show persist

in the real situations. Hence, it is worthwhile to explore the exact solutions. The

one that we will explore here is the spherical limit. For this purpose, we take

V(φ)=−

(φ

)

where



The equation of motion as given by Eq.(6.4.2) becomes

170 6 Systems Far from Equilibrium

=∇

+φ

−

=∇

+φ

−

φ



−



−φ





(6.5.1)

Since φ

=nφ

, in the limit of n →∞, the third term in the R.H.S of Eq.(6.5.1)

is O(1), while the last term is O(n

−1

). Consequently, the last term does not survive

the n →∞limit and we have a linearized equation of motion

=∇

+φ

−φ

φ

(6.5.2)

where φ

 has to be determined self consistently. Writing a(t) =1 −φ

, the

above equation of motion in momentum space is

∂φ

(



∂t

(



k) =a(t)φ

(



k) (6.5.3)

which has the solution

(k, t) =φ

(k, 0)e

−k

b(t)

(6.5.4)

where

b(t) =



a(t



)dt



(6.5.5)

Differentiating Eq.(6.5.5),

= a(t) =1 −





(k, t)φ

(−k, t)



= 1 −



−2k

2b(t)

(6.5.6)

where Eq.(6.3.5) has been used to bring in  for the strength of the initial distri-

bution of φ

.Ast →∞, we expect that a =1 −φ

 will tend to zero and thus for

large t, the L.H.S of Eq.(6.5.6) is negligible, and we have

1 = e

2b(t)



−2k

=e

2b(t)



8πt



D/2

or b(t) =



8πt



2/D



(6.5.7)

The above b(t) leads to

a(t) ∝

6.5 The Structure Factor 171

which indeed vanishes as t →∞. The solution of Eq.(6.5.4) now becomes

(k, t) =φ

(k, 0)





D/4

−k

(6.5.8)

The structure factor S(k, t) follows as

S(k,t) =



(k, t)φ

(−k, t)



=





D/2

−k

= (8πt)

D/2

−k

(6.5.9)

and in the coordinate space

C(r,t)=e

−r

/8t

(6.5.10)

The results showthe expected scaling form of Eqns.(6.3.9) and (6.3.10) with L(t) ∝

1/2

. The structure factor has a Gaussian tail, rather than the power law tail that we

saw occurring for n ≤D. The power law tail was due to the existence of defects. In

systems with n ≥D +1, where there would be no topological defects, we expect

the Gaussian tail to be the correct result.

For the two time correlation function,

S(k,t, t



) =



(k, t)φ

(−k, t



)





8π

√





D/2

−k

(t+t



)

and C(r,t, t



) =



4tt



(t +t



)



D/4

−

4(t+t



)

(6.5.11)

In the limit t t



C(r,t, t



) =





D/4

−





h(r/L) (6.5.12)

the last line following from Eq.(6.3.12), when we deﬁne the exponent

λ through

the dependence on the later time. Clearly,

λ =D/2 in this spherical limit. If we

were to set one of the times equal to zero, then C(r,t,0) would be the correlation

with the initial condition and we would get from Eqns.(6.5.9) and (6.5.11)



k, t, 0) =[8π

√

]

D/2

−k

(6.5.13)

which is just the same as Eq.(6.5.11) with the shorter time t



set equal to some

short time cut off t

. One can deﬁne a response to the initial condition as