Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.


172 6 Systems Far from Equilibrium
G(k, t) =
∂φ
i
(k, t)
∂φ
i
(k, 0)
(6.5.14)
In the spherical limit
G(k, t) =
t
t
0
D/4
e
−k
2
t
(6.5.15)
Clearly,
S(k,t, 0) =G(k, t) (6.5.16)
This result holds in general. The general scaling form for G(k, t), namely
G(k, t) =L
λ
g(kL) (6.5.17)
defines a new exponent λ which is D/2 in the spherical limit. Since correlation
with the initial correlation has the scaling form
C(r,t,0) =L
−
¯
λ
f
r
L
,
we have from Eq.(6.5.12)
¯
λ =D −λ (6.5.18)
For the conserved order parameter, there is an extra −∇
2
on the R.H.S of the
equation of motion. Instead of Eq.(6.5.2), one now finds
˙
φ
i
=−∇
4
φ
i
−∇
2
(1 −φ
2
i
)φ
i
(6.5.19)
in the spherical limit. As before, we work in the momentum space and get instead
of Eq.(6.5.4)
φ
i
(k, t) = φ
i
(k, 0)e
−k
4
t+k
2
b(t)
db
dt
=a(t) = 1 −
k
e
−2k
4
t+2k
2
b(t)
(6.5.20)
At late times, we anticipate a(t) →0 and then
1 =
k
e
−2k
4
t+2k
2
b(t)
=
d
D
k
(2π)
D
e
−2k
4
t+2k
2
b(t)
=
C
D
(2π)
D
k
D−1
dk e
−2
b
2
(t)
t
[(
k
2
t
b(t)
)
2
−
k
2
t
b(t)
]
=
b(t)
t
D/2
C
D
(2π)
D
e
−2β(t)[x
4
−x
2
]
x
D−1
dx (6.5.21)

6.5 The Structure Factor 173
where C
D
=
2π
D/2
(D/2)
is the area of a sphere in D-dimensions and β(t)=b
2
(t)/t.
The integral in Eq.(6.5.21) can be evaluated by the method of steepest descent if
β(t) is very large. Anticipating this, we expand
x
4
−x
2
=−
1
4
+2(x −
1
√
2
)
2
+..........
and performing the Gaussian integration in Eq.(6.5.21)
1 = A
D
b(t)
t
D/2
e
1
2
β(t)
1
β(t)
1/2
= A
D
β
t
D/4
1
√
β
e
β/2
(6.5.22)
The asymptotic solution can be found by writing
0 =ln A
D
+(
D
2
−
1
2
) ln β −
D
4
ln t +
β
2
(6.5.23)
assuming β ln β,
β
D
2
ln t (6.5.24)
justifying the use of steepest descent for t →∞. The structure factor is given by
S(k,t) = e
−2k
4
t
e
2k
2
b(t)
= e
b
2
(t)
t
[2(
k
k
m
)
2
−(
k
k
m
)
4
]
= e
1
2
β(t)[2x
2
−x
4
]
= e
D
4
[2x
2
−x
4
]ln t
= t
D
4
φ(x)
(6.5.25)
where
φ(x) = 1 −(1 −x)
2
x =
k
k
m
and k
m
=
D
8
ln t
t
D/4
is the wavenumber at which the structure factor has a maximum. Had we retained
the term
D−2
4
ln β in Eq.(6.5.23), we would have found a prefactor of O[(ln t)
2−D
4
]
in Eq.(6.5.25). The result of Eq(6.5.25) is interesting because it clearly exhibits
two length scales instead of one required for simple scaling. There is a length scale

174 6 Systems Far from Equilibrium
L ∼t
1/4
, while there is another k
−1
m
∼(
t
ln t
)
1/4
. For simple scaling, the two scales
would have been the same, but here they are logarithmically different. This is an
example of multiscaling. It should be noted, though, that this is a special feature
of the spherical limit.
Exact solutions for the scaling function can also be found for the one dimen-
sional Ising model and the one dimensional XY model. Instead of discussing these
we will now proceed to discuss the approximate theories for finding the scaling
functions.
6.6 Approximate Techniques
Approximate techniques for obtaining the scaling functions revolve around the
replacement of the physical field φ(x, t) by an auxiliary field m(x, t). The field
φ(x,t) is essentially ±1 except at the domain walls where it varies rapidly from
+1 to -1 or vice versa. This discontinuous variation is to be replaced by a smoothly
varying function m. This is generally achieved by a nonlinear transformation φ(m)
which is a function of the ‘sigmoid’ shape. Turning to Eq.(6.3.28), we can write
the velocity of point on the interface as
v =−K =−
∇. ˆn (6.6.1)
where ˆn is the unit vector normal to the wall. The domain wall or the interface
is defined by the zeroes of m(x) i.e. the equation of the interface is m(x) =0.
Consequently, ˆn =
∇m
|
∇m|
and form Eq.(6.6.1)
v =
−∇
2
m +n
α
n
β
∇
α
∇
β
m
|
∇m|
(6.6.2)
To find the equation of motion for m, we note that in a frame of reference moving
with the interface, we must have
dm
dt
=
∂m
∂t
+(v.
∇)m =0 (6.6.3)
Now since v is parallel to
∇m and defined in the same direction
(v.
∇)m =v|
∇m| (6.6.4)
leading to
v =−
1
|
∇m|
∂m
∂t
(6.6.5)
Combining Eqns.(6.6.2) and (6.6.5), we have
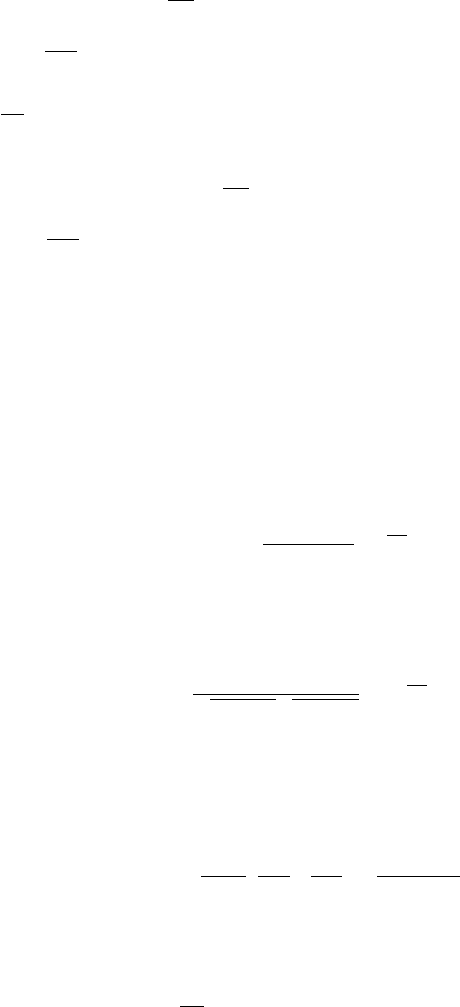
6.6 Approximate Techniques 175
∂m
∂t
=∇
2
m −n
α
n
β
∇
α
∇
β
m (6.6.6)
Since n
α
=
∂
α
m
|
∇m|
, the above equation is nonlinear. To make progress, Ohta, Jasnow
and Kawasaki (OJK) made the simplification of replacing n
α
n
β
by its spherical av-
erage
δ
αβ
D
where D is the dimensionality of space. The equation of motion acquires
the simple form
∂m
∂t
=
˜
D∇
2
m (6.6.7)
where
˜
D =
D−1
D
is a diffusion constant.
The solution of Eq.(6.6.7) requires the specification of initial conditions. In the
absence of long-range correlations, the form of the random initial conditions will
not play a major part in the late-stage scaling. A convenient choice is the Gaussian
distribution for m at t =0, which implies
m(x,0)
= 0
and
m(x,0)m(
x
, 0)
= δ(x −
x
) (6.6.8)
Solving Eq.(6.6.7) and averaging over initial conditions, leads to the correlator
m(1)m(2)
=
(8π
˜
Dt)
D/2
e
−
r
2
8
˜
Dt
(6.6.9)
where 1 and 2 represent space points separated by r. It is important to define the
normalized correlator.
γ(12) =
m(1)m(2)
m
2
(1)
m
2
(2)
=e
−
r
2
8
˜
Dt
(6.6.10)
To calculate the pair correlation function for the original field, we need to know
the joint probability distribution for m(1) and m(2). Given that the distribution is
Gaussian this is straight forward and can be written as
P (m(1), m(2)) =Ne
−
1
2(1−γ
2
)
[
m
2
(1)
S
0
(1)
+
m
2
(0)
S
0
(2)
−2γ
m(1)m(2)
[S
0
(1)S
0
(2)]
1/2
]
(6.6.11)
where γ =γ(12), S
0
(1) =m
2
(1), S
0
(2) =m
2
(2) and the normalization con-
stant N is given by
N =
1
2π
[(1 −γ
2
)S
0
(1)S
0
(2)]
−1/2
(6.6.12)
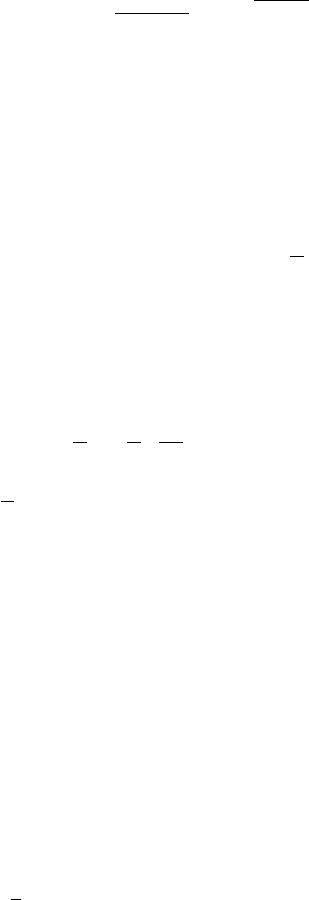
176 6 Systems Far from Equilibrium
We note that 1 and 2 are arbitrary space time points and here γ =γ(12) has to be
thought of as at two different times t
1
and t
2
and it is straightforward to see that
(see Eq.(6.5.11))
γ =
4t
1
t
2
(t
1
+t
2
)
2
D/4
e
−
r
2
4
˜
D(t
1
+t
2
)
(6.6.13)
The pair correlation function is to be found as
C(12) =
φ(m
1
)φ(m
2
)
(6.6.14)
In the scaling regime, one can replace φ(m) by sgn(m) since the walls occupy a
negligible volume fraction. Thus,
C(12) =
sgn[m(1)]sgn[m(2)]
=
2
π
sin
−1
γ (6.6.15)
and together with Eq.(6.6.13) or (6.6.10) as the case may be (unequal time or equal
time), this expression gives the two point correlation function. This expression fits
experimental and simulation data very well. For t
1
t
2
in the two time correlation
function, γ is small and C(r,t
1
,t
2
) becomes approximately,
2
π
γ ∼
2
π
4t
2
t
1
D/4
e
−r
2
/4
˜
Dt
1
,
which gives
¯
λ =
D
2
in this approximation.
In a different approach due to Mazenko, The function φ(m) is chosen in a
clever fashion. It is taken to be the equilibrium interface profile function defined
by
φ
(m) =v
(φ) (6.6.16)
with boundary conditions φ(±∞) =±1, φ(0) =0. Near the wall, the field ‘m’
has the physical significance of a coordinate normal to the wall. Consequently, the
interface length scale does not appear in the problem anymore. Only the domain
scale L(t) is relevant. In this approach the TDGL equation becomes,
˙
φ =∇
2
−φ
(m) (6.6.17)
Multiplying by φ at a different space time point and averaging over initial condi-
tions, we get
1
2
∂
t
C(12) =∇
2
C(12) −
φ
(m(1))φ(m(2))
(6.6.18)
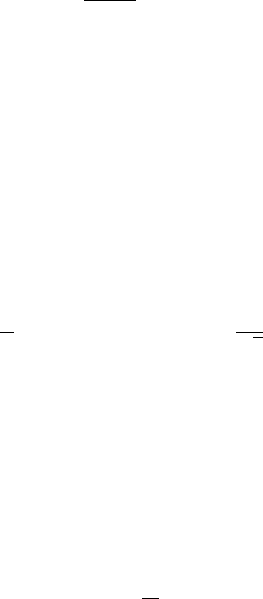
6.6 Approximate Techniques 177
The above relation is exact. To simplify, it was assumed by Mazenko that m can be
treated as Gaussian. This assumption relates the last term to C(12) and one arrives
at a closed system.
To end this section we look at a variant of the above technique due to Mazenko.
Using
˙
φ(m) =˙mφ
(m)
and
∇
2
φ(m) =
∇.(
∇φ(m)) =
∇.(φ
(m)
∇m)
= φ
(m)(∇m)
2
+φ
(m)∇
2
m
we can write the equation of motion as
˙
φ =∇
2
φ −V
(φ)
or φ
(m) ˙m =∇
2
mφ
(m) +φ
(m)(∇m)
2
−φ
(m)
or ˙m =∇
2
m −
φ
(m)
φ
(m)
(1 −(∇m)
2
) (6.6.19)
For a general potential, this is a complicated nonlinear equation. However, the
scaling function is going to be independent of the precise form of the potential and
of the particular choice of initial conditions. Physically, the motion of the interface
is determined by the curvature. The potential V(φ)determines the interface profile
which is irrelevant to the large scale structure. The key step in the approach to be
discussed is the anticipation of the irrelevance of V(φ) and choosing a V(φ) to
simplify Eq.(6.6.19). The choice is
φ
(m) =−mφ
(m) (6.6.20)
with the boundary condition φ(±∞) =±1 and φ(0) =0. The solution is
φ(m) =
2
π
1/2
m
0
dxe
−x
2
/2
=Erf (
m
√
2
) (6.6.21)
With this choice,
˙m =∇
2
m +m(1 −(∇m)
2
) (6.6.22)
Which is still a nonlinear equation, but simpler than the original TDGL equation.
We now show what is the approximation on Eq.(6.6.22) that leads to the OJK
scaling function of Eq.(6.6.15). We introduce an internal colour index α for m and
write the equation of motion as
dotm
α
=∇
2
m
α
+m
α
[1 −
1
N
N
β=1
(
∇m
β
)
2
] (6.6.23)
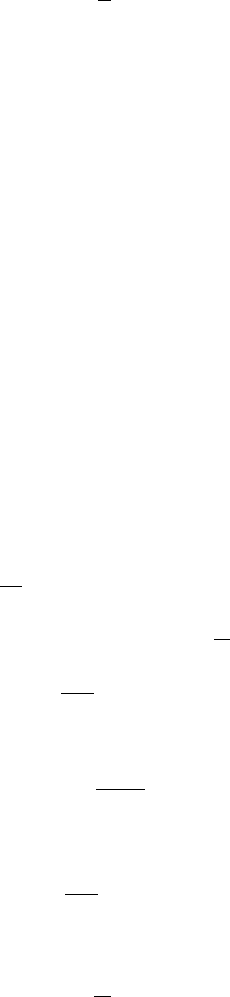
178 6 Systems Far from Equilibrium
N is the number of colour indices and our situation corresponds to N =1. The
OJK result is obtained as N →∞, when
1
N
N
β=1
(
∇m
β
)
2
may be replaced by its
average value. In this limit,
˙m =∇
2
m +a(t)m (6.6.24)
where
a(t) =1 −(∇m)
2
(6.6.25)
The above equations provide a self consistent linear set for m(t).
Taking the initial condition for m to be Gaussian with zero mean and the
correlator prescribed in the Fourier space as
m
k
(0)m
−
k
(0)
=δ
kk
(6.6.26)
the solution of Eq.(6.6.24) is
m
k
(t) =m
k
(0)e
−k
2
t+b(t)
(6.6.27)
where
b(t) =
t
0
dt
a(t
)
leading to
a(t) =
db
dt
=1 −
k
2
e
−2k
2
t+2b(t)
(6.6.28)
After evaluating the sum, one obtains for large t (when
db
dt
can be neglected)
e
2b
≈
4t
D
(8πt)
D/2
(6.6.29)
and hence
a(t) =
D +2
4t
(6.6.30)
Combining Eqns.(6.6.29) and (6.6.27), we get
m
k
(t) =m
k
(0)
4t
D
1/2
(8πt)
D/4
e
−k
2
t
(6.6.31)
and hence
m
k
(t)m
−k
(t)
=
4t
D
(8πt)
D/2
e
−2k
2
t

6.7 Renormalization Group for Late Stage Behaviour 179
leading to
m(1)m(2)=
4t
D
e
−r
2
/8t
(6.6.32)
Turning to the evaluation of the correlation function of the original fields φ,we
note that from Eq.(6.6.32), m is typically t
1/2
for large t and hence at late times
φ(m) takes the values 1 and −1. Consequently, we can take
φ =sgn(m)
and
C(12) =sgn[m(1)]sgn[m(2)]
as we had before. This leads to the OJK result that we had obtained.
6.7 Renormalization Group for Late Stage Behaviour
This section describes the work of Bray which clarified a host of issues regard-
ing the late stage scaling laws. As we have seen before, the RG is an useful tool
whenever scaling laws hold. Consequently, the late stage scaling behaviour should
be amenable to a RG treatment. The idea is to associate the scaling behaviour
with a fixed point of the equation of motion under a RG procedure consisting of a
coarse graining step combined with a simultaneous rescaling of length and time.
Underlying such an idea is the schematic RG flow for the temperature, depicted in
Fig. 6.5 The critical point T
c
corresponds to a fixed point of the RG transfor-
Figure 6.5. Schematic renormalization group flows
mation. At temperatures above T
c
, coarse graining the system leads to a more
disordered system while coarse graining below T
c
leads to a more ordered sys-
tem. This schematic flow is illustrated by arrows in Fig. 6.5. It follows from this
that a quench from any T>T
c
to any T<T
c
should give the same asymptotic
scaling behaviour. Any short range correlation present at the initial temperature
will become irrelevant when L(t) ξ
0
where ξ
0
is the correlation length for the
initial condition. It can be understood from Fig. 6.5 that asymptotic scaling will be
governed by the zero temperature fixed point. This implies that thermal noise can
be dropped from the equation of motion.
180 6 Systems Far from Equilibrium
We will illustrate the use of RG for the conserved order parameter where it
yields an exact answer. The equation of motion (including the thermal noise for
the moment) is given by Eq.(6.3.5)
˙
φ
i
=∇
2
δF
δφ
i
+N
i
Fourier transforming, dividing throughout by λk
2
and including a part representing
non conserved order parameter evolution, we have
1
k
2
+
1
λ
∂φ
i
(k)
∂t
=−
δF
δφ
i
(−k)
+
N
i
k
2
(6.7.1)
If →∞, we are left with a non conserved order parameter, but for any which is
finite, the λ-term in Eq.(6.7.1) is negligible in the long wavelength limit. Requiring
that the canonical distribution be recovered in equilibrium i.e. P(φ)∝e
−F(φ)/k
B
T
,
the usual FDT fixes the correlator of the noise as
ξ
i
(
k, t
1
)ξ
j
(−
k, t
2
)
=2Tδ
ij
δ(t
1
−t
2
)(
1
k
2
+
1
λ
) (6.7.2)
where
ξ
i
(k) =N
i
(k)/ k
2
.
The RG transformation consists of the following steps:
• a) The fourier components φ
i
(k, t) for the hard modes with
b
<k< are
eliminated by solving Eq.(6.7.2) for such modes and substituting the result into
the equation of motion for the soft modes k<
b
. Here is a high momentum
cut off and b is a scale factor for the RG.
• b) A scale change is made k =k
/b in order to reinstate the ultraviolet cut off for
the soft modes at . Additionally time is rescaled as t =b
z
t
. The requirement
that the domain morphology be invariant under this procedure (if the scaling
hypothesis holds) fixes z as thereciprocal of the growth exponenti.e.L(t) ∼t
1/z
.
Finally the field φ
i
(k, t) for k<
b
is rewritten as
φ(
k, t) =
φ(
k
b
,b
z
t
) =b
ζ
φ(
k
,t
) (6.7.3)
The scaling form for the structure factor is
S(
k, t) =t
D/z
g(kt
1/z
)
from Eq.(6.3.10). From the definition of S and Eq.(6.7.3),
S(
k, t) = b
2ζ
φ(
k
,t
)
φ(−
k
,t
)
= b
2ζ
t
D/z
g(k
t
1/z
)
= b
2ζ −Dt
D/z
g(kt
1/z
) (6.7.4)
where ζ =D/2.
6.7 Renormalization Group for Late Stage Behaviour 181
• c) The new equation of motion for the soft modes is interpreted in terms of a
new transport coefficient
and a free energy F
. In addition, terms not origi-
nally present in Eq.(6.7.2) will be included in subsequent RG steps. Similarly,
one must allow for a more general structure for the thermal noise and the
distribution P
0
of initial conditions will also be affected.
• d) Scaling behaviour is associated with a fixed point for which both equation
of motion and P
0
are invariant. In particular, the fixed point free energy is
appropriate to the zero temperature fixed point.
The above procedures are difficult to implement in practice. However, if we assume
the existence of a fixed point which is the same as the assumption of scaling the
recursion relation for the transport coefficient and the temperature T can be
written down exactly. This is sufficient to fix the exponent z. We begin by noting
that the term (k
2
)
−1
in Eq.(6.7.1) is singular at k =0. Now elimination of large
momentum modes will not generate any term in the equation of motion which
is singular at k =0. This elimination can and does affect λ the regular part of the
transport coefficient In Eq.(6.7.1). It is only the rescaling part of the transformation
(step ‘b’) which will affect λ. (This is analogous to our observation in Chapter 2,
that for model B, the relation between z and η is exact, namely z =4 −η. This was
because the mode elimination did not produce any logarithmic divergence and the
exponent was fixed by writing down the transformation under scale transformation
alone and looking for the fixed point).
The scale transformation is now carried out on Eq.(6.7.1). In the process, the
free energy scales as F [{
φ(k
/b)}]=b
Y
F [{
φ(k)}]. This follows from the fact that
the strong coupling fixed point T =0 is attractive and hence T
=b
−y
T and since
Z, the partition function, is invariant, the free energy F scales as mentioned above.
We can now write Eq.(6.7.1) as
[b
ζ +2−z
1
k
2
+b
ζ −z
1
λ
(1 +...)]
∂
φ
(k
)
∂t
+... =−b
y−ζ
δF
δ
φ
(−k
)
+
ξ(
k
/b, b
z
t
)
(6.7.5)
Dividing throughout by b
y−ζ
,
[b
2ζ +2−z−y
1
k
2
+b
2ζ −z−y
1
λ
(1 +..)]
∂
φ
(k
)
∂t
+.. =−
δF
δ
φ
(−k
)
+
ξ
(k
/b, b
z
t
)
(6.7.6)
where the new noise term is
ξ
(k
,t
) =b
ζ −y
ξ
(
k
/b, b
z
t
) (6.7.7)
with the correlator
ξ
i
(k
,t
1
)ξ
j
(−k
,t
2
)
=2b
2ζ −2y−z
Tδ
ij
δ(t
1
−t
2
)
b
2
k
2
+
1
λ
(1 +..)
(6.7.8)
