Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.


182 6 Systems Far from Equilibrium
Writing Eq.(6.7.6) as
1
k
2
+
1
λ
∂
φ
(k
)
∂t
=
δF
δ
φ
(−k
)
+
ξ
(
k
/b, b
z
t
) (6.7.9)
we have
=b
y+z−2−2ζ
At the fixed point
z =2 +2ζ −y (6.7.10)
This evolution is absolutely general. If we work at the ordinary critical point, then T
does not change under the scale tranformations, i.e. y =0. This makes z =2 +2ζ .
In this case, we have the structure factor given by
S(k,L)=k
−2+η
˜g(kL) =L
2−η
g(kL).
This implies
S(k,t) =t
2−η
z
g(kt
1/z
)
and with this choice Eq.(6.7.4) leads to ζ =1 −
η
2
. The dynamic exponent becomes
z =2 +2ζ =4 −η which is the model B answer. Since does not renormalize at
any order and that is the basis for our derivation, z =4 −η is an exact answer
independent of the order of perturbation theory.
If we work at the zero temperature fixed point which is the relevant one for the
problem of quench, then ζ =D/2 as seen from Eq.(6.7.4). This yields
z =2 +D −y (6.7.11)
The exponent y which describes the scaling of the Hamiltonian (hence the energy)
is determined by the excitations in the system. For the scalar order parameter (i.e.
n =1) the excitations are the domain walls of dimension D −1, while for the vector
order parameter (i.e. n ≥2), the excitations are spin waves with dimension D −2.
Hence y =D −1 for n =1 and y =D −2 for n ≥2. Consequently,
z = 3 for n =1
z = 4 for n ≥2
(6.7.12)
The derivation requires no assumptions about the details of the domain growth
kinetics and the central result (Eq.(6.7.11)) is of general validity. It is not restricted
to the O(n) model, but is valid for any symmetry group. One needs only to insert
the appropriate value of η.
6.7 Renormalization Group for Late Stage Behaviour 183
References
1. A. J. Bray, “Theory of Phase Ordering Kinetics” Adv. in Phys. 43 357 (1994).
2. B. Schmittmann and R. K. P. Zia, in ‘Statistical Mechanics of Driven Diffusive
Systems’ Vol.17 of Phase Transition and Critical Phenomena ed. C. Domb and
J. L. Lebowitz, Academic Press (1995).
7
Surface Growth
7.1 Introduction
We begin with a simple model of growth which is called ballistic deposition. In this
model (a one-dimensional version) one begins with a line on which growth will take
place. Particles are now dropped vertically down from a randomly chosen point,
high above, towards the line in question. Gravity plays no role in this process. The
particle stops as soon as it finds a site which has a particle in the nearest neighbour
position. At any instant the interface is the line joining the topmost particle of a
given site.
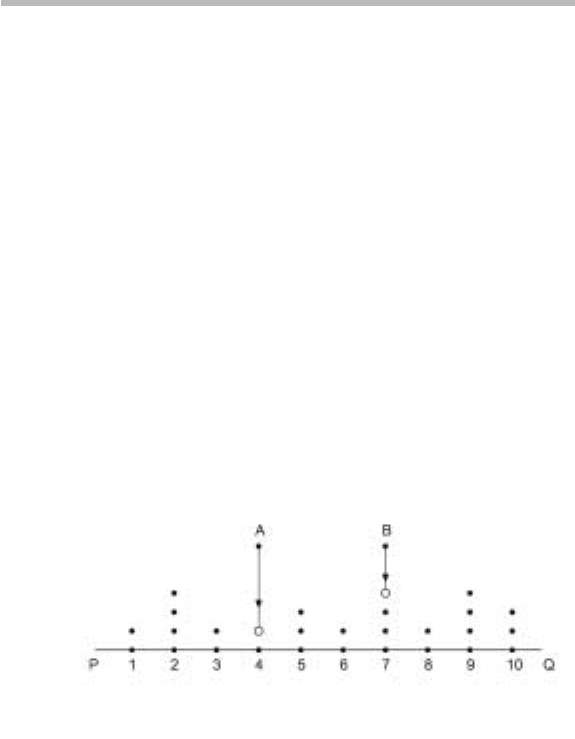
Figure 7.1. Ballistic Deposition Model
186 7 Surface Growth
In Fig. 7.1 we show a ballistic deposition model with ten sites along the line
PQ. particles A and B are dropped from above and will stick in the positions
shown according to the rules in the text. The mean height of the interface at any
instant is
¯
h(t) =
1
N
N
i=1
h
i
(t) (7.1.1)
where h
i
(t) is the height of the interface at the site i and N is the total number of
sites. In Fig. 7.1 N =10.
The interface will not be flat. There will be fluctuations around
¯
h(t) and this
fluctuation is defined as
W(t)=
1
N
N
i=1
(h
i
(t) −
¯
h(t))
2
1/2
(7.1.2)
It is interesting to observe what the width does as a function of time. In the initial
stage, the width increases with time. This increase is expressed as
W(t)∝t
β
(t t
c
) (7.1.3)
For t t
c
, it is seen that the width saturates, i.e. it no longer increases with time
and reaches a constant value. This constant value depends upon the number of sites
N in the problem or in other words on L, the size of the system. As can be seen
from Fig. 7.2, the time t
c
at which the width begins to roll over to a constant value
also depends on the system size L.
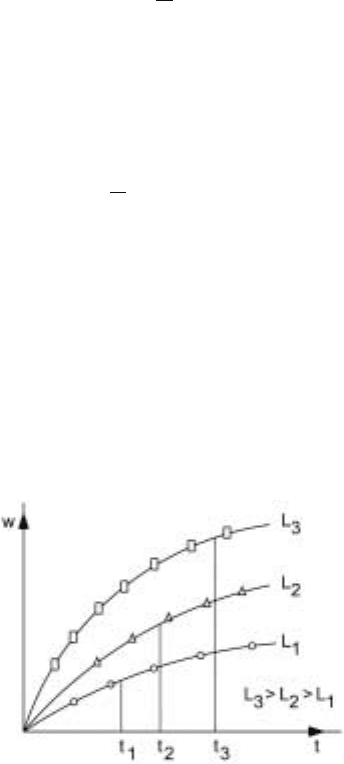
Figure 7.2. Interface width as a function of time for different system sizes
Here we plot the width as a function of time for different system sizes. The times
at which the different sized systems roll over towards saturation values are shown
as t
1
,t
2
and t
3
. These dependences on the system size can be expressed as
7.1 Introduction 187
W (L) ∝L
α
(t t
c
) (7.1.4)
and
t
c
∝L
z
(7.1.5)
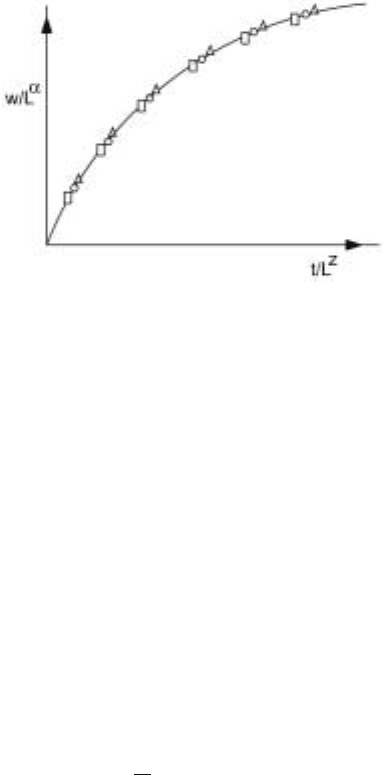
It is now observed that the data on different system sizes (squares, triangles and
circles) collapse on a single curve if we choose to plot W/L
α
against t/L
z
. This
is shown in Fig. 7.3 and is mathematically expressed as
Figure 7.3. Scaling plot for the width of the interface
W = L
α
f(t/t
c
)
= L
α
f(t/L
z
) (7.1.6)
where f(x)is called a scaling function. It is clear that as x →∞, f(x)will tend to
a constant. For x →0, i.e. t t
c
, we must have W ∼t
β
, and this can be achieved
only if f(x)∼x
β
, with βz=α. This means that the three exponents α, β and z are
not independent. They are related by the relation,
α =βz (7.1.7)
The interesting question is why the system shows the saturation of the width at
large times. This has to do with the existence of correlations between the different
sites. The correlation comes from the fact that a particle can stop at any site which
has a nearest neighbour. This builds up correlation in the lateral direction. The
correlation function can be calculated as
C(j, t) =
1
N
N
i=1
(h
i
−
¯
h)(h
i+j
−
¯
h) (7.1.8)

188 7 Surface Growth
One finds
C(j, t) ∝j
2α
(t t
c
) (7.1.9)
and
C(j, t) ∝j
2β
(t t
c
) (7.1.10)
One can define a correlation length ξ ∝t
1/z
, such that
C(j, t) ∝j
2α
g(j/ξ) (7.1.11)
For j ξ (i.e. t t
c
), g(x) ∼x
−2α
, so that Eq.(7.1.10) may be regained, with
α/z =β as in Eq.(7.1.7). For j ξ (i.e. t t
c
), we need to have g(∞) →constant
to reproduce Eq.(7.1.9). The correlation length ξ expresses the correlation devel-
oped in the lateral direction. For α>0, the fluctuation at site i is correlated with
fluctuation at site i +j and the correlation grows with growing j . This means
fluctuations exist all along the surface and the surface is said to be rough.
7.2 Edwards Wilkinson(EW) Model
We now make the model even simpler. A particle falls from above from a randomly
chosen site but sticks only when it comes to the top of the column already standing
at that site. This means there is no lateral correlation. The growth of the height
h(x, t) at any point x is determined by the flux φ(x,t) at that point and we have
∂
∂t
h(x, t) =φ(x,t) (7.2.1)
Now φ(x,t) will have a mean and a fluctuating part and we can decompose it as
φ(x,t)=F +η(x, t). clearly, φ(x,t)=F and η(x, t)=0. The mean rate at
which the particles fall is F and η is the random fluctuation about that mean. This
random fluctuation η(x, t) is prescribed through its correlation which can be taken
as Gaussian
η(x, t)η(x
,t
)=2Nδ(x −x
)δ(t −t
) (7.2.2)
We now have
∂h
∂t
=F +η(x, t) (7.2.3)
with the solution
h(x, t) =Ft +
t
0
η(x, t
)dt
(7.2.4)

7.2 Edwards Wilkinson(EW) Model 189
Clearly,
¯
h =h(x, t)=Ft
and the fluctuation
W(t)=(h(x, t) −
¯
h)
2
=
t
0
η(x, t
)dt
t
0
η(x, t
)dt
=
t
0
t
0
2Nδ(t
−t
)dt
dt
= 2Nt
The correlation
C(r) =(h(x +r,t)−
¯
h)(h(x,t)−
¯
h)
=
t
0
t
0
2dt
dt
η(x +r,t
)η(x, t
)
= 0ifr =0 (7.2.5)
which shows the lack of correlation that we talked about. Correlations will develop
if the particles are allowed to slide after sticking at the top of the column and come
to rest when it lands in a local minimum. This is equivalent to saying that there can
be smoothening in the lateral direction and measuring h(t) from its mean position
¯
h(t) we can now write the equation of motion in this model as
∂h
∂t
=ν
∂
2
h
∂x
2
+η (7.2.6)
This is the EW model that we have already talked about in Chapter 2.
In writing down equations of motion of the above variety it is generally necessary
to pay heed to certain symmetries. For the structure
∂h
∂t
=G(x,h,t)+η(x, t) (7.2.7)
these are
• i) time translation invariance
: The growth equation should not depend on time.
This rules out explicit time dependence in G
• ii) translation invariance in the growth direction
: The growth rule should be
independent of the origin of h, i.e. G cannot contain h.
• iii) translational invariance perpendicular to the direction of growth
: this rules
out explicit x-dependence in G.
• iv) rotation and inversion symmetry about the growth direction
: this ensures
that vectors such as
∇h and
∇∇
2
h do not enter the function G.
190 7 Surface Growth
• v)up/down symmetry in h: the interface fluctuations are similar with respect
to the mean interface height. For non-equilibrium properties of surfaces this
symmetry may be broken as it is for the Kardar-Parisi-Zhang (KPZ) system
discussed briefly in Chapter 1.
The above arguments lead us to expect only derivatives of h in the function G.
Which derivatives are we going to keep? In general we expect h(x, t) to be a
slowly varying function of x and hence it is the lowest order derivatives which
should get priority. In other words, one does a long wavelength approximation.
After this digression, we return to the EW model and carry out the scale transfor-
mations
x → x
=bx
t → t
=tb
z
h → h
=b
α
h and
η → η
=b
µ
η
The equation of motion should remain unchanged under these transformations.
Carrying out this set of transformations on Eq.(7.1.17)
b
z−α
∂h
∂t
= νb
2−α
∂
2
h
∂x
2
+η
b
−µ
∂h
∂t
= νb
2−z
∂
2
h
∂x
2
+η
b
α−µ−z
(7.2.8)
with Eq.(7.1.13) becoming
b
−2µ
η
(x
1
,t
1
)η
(x
2
,t
2
)=2Nδ(x
1
−x
2
)δ(t
1
−t
2
)b
1+z
η
(x
1
,t
1
)η
(x
2
,t
2
)=2Nb
1+2µ+z
δ(x
1
−x
2
)δ(t
1
−t
2
) (7.2.9)
The equation of motion in the primed variables will be
∂h
∂t
= ν
∂
2
h
∂x
2
+η
η
(x
1
,t
1
)η
(x
2
,t
2
)=2Nδ(x
1
−x
2
)δ(t
1
−t
2
) (7.2.10)
if
z = 2
1 +2µ =−z =−2or µ =−3/2
and α −µ = z =2or α =1/2 (7.2.11)
The behaviour of the width W(t) can be found as
W(t) =h(t)
2
1/2
=b
−α
[h
(tb
z
)
2
]
1/2
= b
−α
W
(tb
z
) (7.2.12)

7.2 Edwards Wilkinson(EW) Model 191
setting tb
z
=1, we have
W(t)=t
α/z
=t
1/4
(7.2.13)
From the definition of Eq.(7.1.3), we find β =1/4 and from Eq.(7.1.7), we have
α =1/2.
If the substrate happens to be D-dimensional, then x is a D-dimensional vector
and the effect of D shows up in Eq.(7.2.9), which now reads
η
(x
1
,t
1
)η
(x
2
,t
2
)=2Nb
D+2µ+z
δ(
x
1
−
x
2
)δ(t
1
−t
2
) (7.2.14)
The invariance under the scale transformation now means
z = 2
D +2µ =−z =−2orµ =−
1
2
(2 +D)
and α −µ = z =2orα =2 +µ =1 −
D
2
(7.2.15)
We then have, by comparing with Eq.(7.2.13)
β =
1
4
(2 −D)
α =
1
2
(2 −D)
z = 2 (7.2.16)
The above conclusion could also have been arrived at by a direct integration of the
EW equation. This exact solution is possible because it is a linear equation. In the
Fourier space in D-dimension we can write Eq.(7.2.6) as
∂
∂t
h(
k, t) =−νk
2
h(
k, t) +η(
k, t) (7.2.17)
with
η(
k
1
,t
1
)η(
k
2
,t
2
)=2Nδ(
k
1
+
k
2
)δ(t
1
−t
2
) (7.2.18)
The solution of Eq.(7.2.17)
h(
k, t) =e
−νk
2
t
t
0
η(k, t
)e
νk
2
t
dt
(7.2.19)
with the initial condition that h(
k, t) =0 at t=0. The correlation function in Fourier
space is

192 7 Surface Growth
C(k,t
1
,t
2
) =h(
k
1
,t
1
)h(−
k
2
,t
2
)
= e
−νk
2
(t
1
+t
2
)
t
1
0
t
2
0
η(
k, t
)η(−
k, t
)dt
dt
= 2Ne
−νk
2
(t
1
+t
2
)
t
1
0
dt
t
2
0
dt
δ(t
−t
)e
νk
2
(t
+t
)
(7.2.20)
If t
2
>t
1
, then we need to do the integration over t
first and this leads to
C(k,t
1
,t
2
) = 2Ne
−νk
2
(t
1
+t
2
)
t
1
0
dt
e
2νk
2
t
=
N
νk
2
[e
−νk
2
(t
2
−t
1
)
−e
−νk
2
(t
1
+t
2
)
] (7.2.21)
For large values of t
1
and t
2
we can drop the second term and we get
C(k,t
1
,t
2
) =
N
νk
2
e
−νk
2
|t
12
|
(7.2.22)
where t
12
=t
2
−t
1
and the mod sign appears because in Eq.(7.2.22), the first term
would involve t
1
−t
2
if t
1
were to be greater than t
2
. In coordinate space, the
correlation function will be
C(r
12
,t
12
) =
1
(2π)
D/2
d
D
k
k
2
e
−νk
2
|t
12
|
e
−i
k.r
12
(7.2.23)
For t
12
=0 (equal time correlation function), we have
C(r
12
) =
1
(2π)
D/2
d
D
k
k
2
e
−i
k.r
12
= A(D)r
2−D
12
(7.2.24)
where A(D) is a constant whose value depends on the dimensionality of space.
Comparing with Eq.(7.1.9) we find α =1 −
D
2
in agreement with Eq.(7.2.16). For
arbitrary t
12
,
C(r
12
,t
12
) =
1
(2π)
D/2
d
D
k
k
2
e
−ν|t
12
|[k
2
+
i
k.r
12
ν|t
12
|
]
=
1
(2π)
D/2
d
D
k
k
2
e
−
r
2
12
4ν|t
12
|
e
−ν|t
12
|[
k+
ir
12
ν|t
12
|
]
2
=|t
12
|
1−D/2
f(
r
2
12
ν|t
12
|
)
= r
2−D
12
g(
r
2
12
ν|t
12
|
) (7.2.25)
