Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.


7.3 Kardar-Parisi-Zhang (KPZ) Model 193
The scaling function g(x) has the property that g(x) →const ant as x →∞,
which ensures that the conclusions of Eq.(7.2.25) and Eq.(7.1.24) agree. The fact
that α =1 −D/2 implies that α changes sign as we vary the dimensionality of the
substrate. The exponent α is a measure of the roughness of the interface. If we have
a fluctuation δh at a point r
1
of the interface , then the correlation function C(r
12
)
tells us what is the likelihood that there will be fluctuation at a point r
2
, a distance
r
12
away from r
1
.IfC(r
12
) grows with r
12
, then fluctuations exist all over the
interface and the interface is rough. If C(r
12
) decays with r
12
then the fluctuation
at r
1
is localized and its effect is not felt at a point somewhat removed from r
1
.
This makes the interface smooth. If α>0, then C(r
12
) grows with r
12
and we have
a rough interface. If α<0, the correlation function decays and we have a smooth
interface. Thus for D ≤2, we have a rough interface and for D>2, the interface is
smooth. Larger the dimension of the substrate, more effective is the smoothening
effect of ν∇
2
h which smoothes out the growing surface. The smoothening term is
like a surface tension.
7.3 Kardar-Parisi-Zhang (KPZ) Model
We now want to include nonlinear terms in the EW model and see if the predictions
about the exponents can be changed by the nonlinearity. The logic behind adding
the nonlinear term is that as the interface grows, the growth at any particular point
should occur preferentially along the local normal. As shown in Fig. 7.4, the height
changes by an amount δh at point Q in time δt due to local growth at the point P .
The interface velocity at the point P is v in the normal direction and hence the right
angled triangle gives
Figure 7.4. Direction of velocity of the growing interface

194 7 Surface Growth
δh =vδt sec θ
=vδt
1 +tan
2
θ
=vδt
1 +(
∂h
∂x
)
2
vδt +
1
2
vδt(
∂h
∂x
)
2
(7.3.1)
This leads to
∂h
∂t
=v +
1
2
v(
∂h
∂x
)
2
+.... (7.3.2)
which implies that the growth equation for h should contain (
∇h)
2
as the most
important nonlinear contribution. The effect is clearly to induce lateral correlation
since what has happened is that the growth in the normal direction at a given point
has induced growth at a neighboring point. We, consequently, generalize Eq.(7.2.6)
to
∂h
∂t
=ν∇
2
h +
λ
2
(
∇h)
2
+η (7.3.3)
which is the D-dimensional KPZ equation.
We first carry out a scale transformation so that the coordinates are rescaled by
a factor b as in section 7.2 and the corresponding h, t and η by factors of b
α
, b
z
and b
µ
respectively. Under these rescalings Eq.(7.3.3) becomes
b
z−α
∂(hb
α
)
∂(tb
z
)
=νb
2−α
∇
2
(hb
α
) +
λ
2
b
2−2α
[
∇(bh)]
2
+ηb
µ
b
−
1
2
(D+2)
In the above µ remains at µ =−
1
2
(D +2) as in Eq.(7.2.15) to keep the noise
correlator unchanged. Writing h
=hb
α
and t
=tb
z
,wenowhave
∂h
∂t
=νb
2−z
∇
2
h
+
λ
2
b
2−z−α
(
∇
h
)
2
+η
b
D−z
2
+α
(7.3.4)
If the form of this equation is to remain invariant, then we must havez =2, z =2 −α
and α =
z−D
2
. This clearly cannot be as we have three equations for two unknowns.
The reason should be apparent from our discussions in Chapters 3 and 4.Inthe
presence of nonlinear terms, coupling constant and diffusion coefficients change
under the scale transformation. Consequently, we should not have started with the
assumption that ν, λ and N do not change.
To test the relevance of the nonlinear term, we let z and α remain at the EW
values (ν and N unchanged) and ask how λ changes. From Eq.(7.3.4), it is imme-
diately clear that
λ
=b
2−z−α
λ =b
−α
λ =b
D−2
2
λ (7.3.5)

7.3 Kardar-Parisi-Zhang (KPZ) Model 195
Our interest lies in the long distance properties, i.e. when the primed equation
probes a distance scale which is higher and for that b has to be smaller than
unity. Accordingly λ
>λ if D<2. Under a scale transformation, the nonlinear
term grows for substrate dimension less than 2. On the other hand for D>2, the
nonlinear term is irrelevant for long distance behaviour and the exponents of the
KPZ equation should asymptotically be the same as for the EW equation.
We can look at the KPZ equation in yet another fashion. If we define v =−
∇h
then Eq.(7.3.3)becomes
−
∂ v
∂t
=−ν∇
2
v +
λ
2
∇v
2
+
∇η (7.3.6)
which is
(
∂
∂t
+λv.
∇)v =ν∇
2
v −
∇η (7.3.7)
If λ =1, then this is the same as a pressure-less Navier Stokes equation which is
known as Burger’s equation. Burger’s equation shows Galilean invariance i.e. it
remains unchanged under x →x
=x −v
0
t and t
=t and v →v
=v −v
0
. This
of course requires that λ be kept at unity and it suggests that λ does not renormalize
in Eq.(7.3.7) which from Eq.(7.3.5) would yield
α +z =2 (7.3.8)
This is a consequence of Galilean invariance of Eq.(7.3.3) which can be written as
an invariance under the transformation h →h
+x, x
=x −λt, t
=t
Finally note that the Langevin equation of the EW variety i.e.
∂h
∂t
=ν
∂
2
h
∂x
2
+η
with
η(x, t)η(x
,t
)=2Nδ(x −x
)δ(t −t
)
can be cast as
∂h
∂t
=
δF
δh
+η
where F =ν
dx(
∂h
∂x
)
2
and
δF
δh
is the functional derivative. This leads to the
Fokker-Planck equation
∂P
∂t
=
δ
δh
(P
δF
δh
) +N
∂
2
P
∂h
2
(7.3.9)
according to our considerations in Chapter 1. We see that this Fokker-Planck equa-
tion leads to an equilibrium distribution
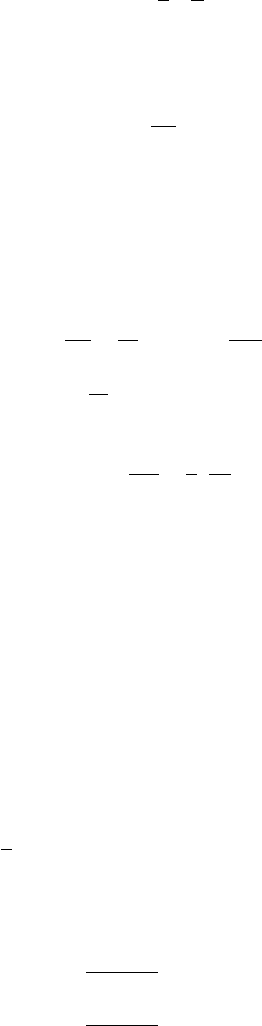
196 7 Surface Growth
P
eq
∝e
−
ν
N
(
∂h
∂x
)
2
dx (7.3.10)
Thus the EW model has an equilibrium distribution associated with it. The KPZ
equation cannot be cast in the form
˙
h =
δF
δh
+η
and hence one suspects that there are no equilibrium distributions associated with
it. We note that for a Langevin equation
˙
h =G(h) +η
One can always write a Fokker Planck equation
∂P
∂t
=
δ
δh
(P G) +N
δ
2
P
δh
2
(7.3.11)
If G does not have the structure
δF
δh
, then it is not clear if an equilibrium distribution
can be found. For the KPZ equation with
G =ν
∂
2
h
∂x
2
+
λ
2
(
∂h
∂x
)
2
we can see the equilibrium distribution of Eq.(7.3.10) is also the equilibrium dis-
tribution in this case. This is a special feature of a one dimensional substrate. It is
not true in higher dimensions.
7.4 KPZ Equation and the Renormalization Group
In this section, we will implement the RG procedure on the KPZ equation to find
the scaling behaviour of the diffusion coefficient, coupling constants etc. This will
follow very closely the procedure shown in Chapter 3. Consequently, we will start
out directly by writing the Fourier transform of Eq.(7.3.3) as
−iωh(
k, ω)=−νk
2
h(
k, ω)
−
λ
2
p, ω
1
p.(
k −p)h( p, ω
1
)h(
k −p, ω −ω
1
) +η(
k, ω)
(7.4.1)
where
h(r,t) =
1
(2π)
D+1
d
D
kdωh(
k, ω)e
i(
k.r−ωt)
and η(r,t) =
1
(2π)
D+1
d
D
kdωη(
k, ω)e
i(
k.r−ωt)
(7.4.2)
7.4 KPZ Equation and the Renormalization Group 197
with
η(
k, ω)η(
k
,ω
)=2Nδ(
k +
k
)δω +ω
The range of momentum integration is from 0 to λ and the frequency ranges from
0to. We split, as usual, the momentum range from 0 to
b
and
b
to , while
the frequency range is split from 0 to
b
z
and
b
z
to , where b is a number larger
than unity. In the momentum range 0 to
b
and frequency range 0 to
b
z
the height
variable is h
<
. As before the idea is to first find the equation of motion for h
<
.
Writing
h(r,t) =
1
(2π)
D+1
b
0
d
D
k
b
z
0
dωh
<
(
k, ω)e
i(
k.r−ωt)
+
1
(2π)
D+1
b
d
D
k
b
z
dωh
>
(
k, ω)e
i(
k.r−ωt)
(7.4.3)
we have in the range 0 <k<
b
,0<ω<
b
z
−iωh
<
(
k, ω) =−νk
2
h
<
(
k, ω)−
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
)
−λ
p.(
k −p)h
<
( p, ω
1
)h
>
(
k −p, ω −ω
1
)
−
λ
2
p.(
k −p)h
>
( p, ω
1
)h
>
(
k −p, ω −ω
1
) +η
<
(
k, ω)
(7.4.4)
In the other range,
−iωh
>
(
k, ω) =−νk
2
h
>
(
k, ω)−
λ
2
p.(
k −p)h
>
( p, ω
1
)h
>
(
k −p, ω −ω
1
)
−λ
p.(
k −p)h
<
( p, ω
1
)h
>
(
k −p, ω −ω
1
)
−
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
) +η
>
(
k, ω)
(7.4.5)
The procedure now is to solve for h
>
from Eq.(7.4.5) and insert the result in
Eq.(7.4.4). Since the solution for h
>
(
k, ω) will depend on η
>
, the final step will
have to be an averaging over η
>
before we have an equation of motion for h
<
.
Accordingly, we find
h
(0)
>
=
η
>
−iω +νk
2
(7.4.6)
if we expand h
>
as h
>
=h
(0)
>
+λh
>
(1) +λ
2
h
(2)
>
+.... Clearly,

198 7 Surface Growth
(−iω +νk
2
)h
(1)
>
=−
p.(
k −p)h
<
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)
−
1
2
p.(
k −p)h
(0)
>
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)
−
1
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
) (7.4.7)
(−iω +νk
2
)h
(2)
>
=−
p.(
k −p)h
<
( p, ω
1
)h
(1)
>
(
k −p, ω −ω
1
)
−
1
2
p.(
k −p)h
(0)
>
( p, ω
1
)h
(1)
>
(
k −p, ω −ω
1
)
−
1
2
p.(
k −p)h
(1)
>
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)
(7.4.8)
and so on. Using Eq.(7.4.7) in Eq.(7.4.4), we have to O(λ
2
)
−iωh
<
(
k, ω) =−νk
2
h
<
(
k, ω)−
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
)
+λ
p.(
k −p)h
<
( p, ω
1
)[h
(0)
>
(
k −p, ω −ω
1
)
+λh
(1)
>
(
k −p, ω −ω
1
)]
+
λ
2
p.(
k −p)[h
(0)
>
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)
+λh
(0)
>
( p, ω
1
)h
(1)
>
(
k −p, ω −ω
1
)
+λh
(1)
>
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)]+η
<
(
k, ω) (7.4.9)
where h
(1)
>
is to be substituted from Eq.(7.4.7). Instead of writing it out fully, we
recall the third step that needs to be done. We need to average over η and from
Eq.(7.4.6), we see that h
(0)
>
is directly proportional to η. We will write out only the
surviving terms after this process of averaging (ignoring a constant term which can
be removed by a shift of the mean value)
−iωh
<
(
k, ω) = νk
2
h
<
(
k, ω)−
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
)
λ
2
2
p.(
k −p)h
<
(q,ω
2
)
q.( p −q)
−iω
1
+νp
2
h
(0)
>
( p −q,ω
1
−ω
2
)
×h
(0)
>
(
k −p, ω −ω
1
)
+
λ
2
2
p.(
k −p)h
<
(q,ω
2
)
q.(
k −p −q)
−i(ω −ω
1
)
2
+ν(
k −p)
2
×h
(0)
>
(
k −p −q,ω −ω
1
−ω
2
)h
(0)
>
( p, ω
1
)
+trilinear terms in h
<
+η
<
(7.4.10)
7.4 KPZ Equation and the Renormalization Group 199
We now note that
ω
1
,ω
2
, p,q
p.(
k −p)h
<
(q,ω
2
)q.( p −q)
(−iω
1
+νp
2
)
×h
(0)
>
( p −q,ω
1
−ω
2
)h
(0)
>
(
k −p, ω −ω
1
)
=
p,ω
1
2N
p.(
k −p)h
<
(
k, ω)
(−iω
1
+νp
2
)
×
k.( p −
k)
ν
2
(
k −p)
4
+(ω −ω
1
)
2
=
p
N
ν
h
<
(
k, ω)
(
k −p)
2
×
p.(
k −p)
k.( p −
k)
−iω +νp
2
+ν(
k −p)
2
and
ω
1
,ω
2
, p,q
2N p.(
k −p)
k.(−p)h
<
(
k, ω)
[ω
2
+ν
2
p
4
][−i(ω −ω
1
) +ν(
k −p)
2
]
=−
p
N
ν
h
<
(
k, ω)
(
k. p)
2
×
p.(
k −p)(
k. p)
−iω +νp
2
+ν(
k −p)
2
Dropping the trilinear term in Eq.(7.4.10), we can write
−iωh
<
(
k, ω) =−νk
2
h
<
(
k, ω)+
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
)
−h
<
(
k, ω)
λ
2
2
N
ν
d
D
p
(2π)
D
p.(
k −p)
−iω +νp
2
+ν(
k −p)
2
×[
k. p
p
2
+
k.(
k −p)
(
k −p)
2
]+η
<
(
k, ω) (7.4.11)
The momentum integral needs to be performed over the range
b
< |p|< and
hence we need only the small-k part. Accordingly, one works to the lowest order
in |
k| to write the integrand as
p.(
k −p)
−iω +νp
2
+ν(
k −p)
2
×
k. p
p
2
+
k.(
k −p)
(
k −p)
2
≈[( p.
k)p
2
−2( p.
k)
2
+p
2
k
2
−p
2
( p.
k)]×
( p.
k −p
2
)
2νp
2
p
4
≈
2( p.
k)
2
−p
2
k
2
2νp
4
We note that this term is O(k
2
) and hence the third term on the R.H.S is an addition
to the first term. In doing the integral, the averaging over cos
2
θ produces a factor
D
−1
and Eq.(7.4.11) becomes

200 7 Surface Growth
−iωh
<
(
k, ω) =−
ν +
λ
2
N(2 −D)
4ν
2
D
b
d
D
p
(2π)
D
1
p
2
k
2
h
<
(
k, ω)
+
λ
2
p.(
k −p)h
<
( p, ω
1
)h
<
(
k −p, ω −ω
1
)
+η
<
(
k, ω) (7.4.12)
The elimination of small scales leads to an effective viscosity ¯nu given by
¯ν =ν +
λ
2
N(2 −D)
4ν
2
D
b
d
D
p
(2π)
D
1
p
2
(7.4.13)
The correlation function for h(k, ω) has the expansion (to O(λ
2
))
h(
k, ω)h(
k
,ω
)=h
(0)
(
k, ω)h
(0)
(
k
,ω
)+λh
(0)
(
k, ω)h
(1)
(
k
,ω
)
+λh
(1)
(
k, ω)h
(0)
(
k
,ω
)+λ
2
h
(0)
(
k, ω)h
(2)
(
k
,ω
)
+λ
2
h
(2)
(
k, ω)h
(0)
(
k
,ω
)+λ
2
h
(1)
(
k, ω)h
(1)
(
k
,ω
)
=
2Nδ(
k +
k
)δ(ω +ω
)
ω
2
+ν
2
k
4
+λ
2
[h
(2)
(
k, ω)h
(0)
(
k
,ω
)
+h
(1)
(
k, ω)h
(1)
(
k
,ω
)+h
(0)
(
k, ω)h
(2)
(
k
,ω
)]
(7.4.14)
where
h(
k, ω)=h
(0)
(
k, ω)+λh
(1)
(
k, ω)+h
(2)
(
k, ω)+....
and by inserting this in Eq.(7.4.1) and equating like powers of λ
h
(0)
(
k, ω) =
η(k, ω)
−iω +νk
2
(−iω +νk
2
)h
(1)
(
k, ω) =−
1
2
p.(
k −p)h
(0)
( p, ω
1
)h
(0)
(
k −p, ω −ω
1
)
(−iω +νk
2
)h
(2)
(
k, ω) =−
p.(
k −p)h
(1)
( p, ω
1
)h
(0)
(
k −p, ω −ω
1
)
All possible contractions of the string of h
(0)
are considered and finally we find
h(
k, ω)h(
k
,ω
)
=δ(
k +
k
)δ(ω +ω
)[
2N
ω
2
+ν
2
k
4
+
λ
2
ν
2
N
2
ω
2
+ν
2
k
4
+
d
D
p
p
2
(
k −p)
2
{
[p.(
k −p)]
2
−iω +ν[p
2
+(
k −p)
2
]
+c.c}] (7.4.15)
To see what kind of dressing of N is implied, it is best to check the integral over
ω, and then we find that N is changed to a N
eff
, where
7.4 KPZ Equation and the Renormalization Group 201
N
eff
=N +
λ
2
N
2
2ν
3
d
D
p
p
2
(
k −p)
2
[p.(
k −p)]
2
k
2
+p
2
+(
k −p)
2
(7.4.16)
This relation makes apparent the effect of thinning of degrees of freedom. The
coefficient N will change to
¯
N given by
¯
N =N +
λ
2
N
2
4ν
3
b
d
D
p
p
2
(7.4.17)
To see the effect of the removal of degrees of freedom in λ, we need to go to the
third order in λ in Eq.(7.4.9). The O(λ
3
) terms in Eq.(7.4.9) would be
p.(
k −p)h
<
( p, ω
1
)h
(2)
>
(
k −p, ω −ω
1
)
+
1
2
p.(
k −p)[h
(0)
>
( p, ω
1
)h
(2)
>
(
k −p, ω −ω
1
)
+h
(1)
>
( p, ω
1
)h
(1)
>
(
k −p, ω −ω
1
)
+h
(2)
>
( p, ω
1
)h
(0)
>
(
k −p, ω −ω
1
)]
The fields h
(1)
>
and h
(2)
>
have to be substituted from Eqns.(7.4.7) and (7.4.8) and
the h
(0)
>
averaged over. We want those terms which have the structure
d
D
p
(2π)
D
h
<
( p)h
<
(
k −p)(
k) p.(
k −p)
after the averaging. It will be seen that (
k) =0 for small k.
At the end of the above process, we have removed the degrees of freedom at
the high momentum end. The cut off now is
b
which has to be restored to by
a scale transformation. The effect of a scale transformation can be read off from
Eq.(7.3.4). If the scale of measuring is changed by b as has been done in changing
the cut off to
b
, then the b occurring in Eq.(7.3.4)is to be interpreted as b
−1
in the
present context and we have the total change as (K
D
=
S
D
(2π)
D
), S
D
being the area
of the D −1 dimensional hypersurface)
ν
= b
z−2
ν
1 +
λ
2
N(2 −D)K
D
4ν
3
D
b
d
D
p
p
3−D
(7.4.18)
N
= b
−2α−(D−z)
N
1 +
λ
2
NK
D
4ν
3
b
d
D
p
p
3−D
(7.4.19)
λ
= b
z+α−2
λ (7.4.20)
For b 1, we can expand b
z−2
1 +(z −2) ln b +O(ln b)
2
and similarly for the
other powers of b. The integrals give a term proportional to ln b, when we evaluate
them in D =2 and thus

202 7 Surface Growth
ν
= ν
1 +
(z −2) +
¯
λ
2
(2 −D)
4D
ln b
N
= N
1 +
z −D −2α +
¯
λ
2
4
ln b
λ
= λ[1 +{z +α −2}ln b]
Writing b =1 +δl,wehave
dν
dl
= ν
z −2 +
¯
λ
2
2 −D
4D
(7.4.21)
dN
dl
= N
z −D −2α +
¯
λ
2
4
(7.4.22)
dλ
dl
= λ[z +α −2] (7.4.23)
where
¯
λ
2
=
λ
2
NK
2
ν
3
The flow of
¯
λ is clearly,
d
¯
λ
dl
=
¯
λ
2 −D
2
−
¯
λ
2
4D
(3 −2D)
(7.4.24)
This modified coupling constant can flow to two different fixed points. One is
¯
λ =0. This is clearly unstable if D<2. Consequently, the KPZ answers will be
different from EW if the substrate dimension is below 2. For D>2,
¯
λ =0isa
stable fixed point and one expects to see a EW like phase but with α =0 since
z=2. If the substrate dimension is D =1, then one gets a non trivial fixed point
¯
λ
∗
2
=2. The stability can be tested by evaluating the derivative of
¯
λ
2
−
¯
λ
3
4
at the
fixed point. It is
1
2
−
3
4
¯
λ
∗
2
=−1 and hence the fixed point is stable. Thus at D =1,
the interface behaviour will be governed by the non trivial fixed point
¯
λ
∗
2
=2.
From Eq.(7.4.21), we find
z = 2 −
1
2
(7.4.25)
α = 2 −z =
1
2
(7.4.26)
at this non trivial fixed point. Consequently, we we have a rough interface in D=1
determined by the strong coupling fixed point. The values obtained in Eqns.(7.4.25)
and(7.4.26) happen to be exact. This is fortuitous. For D>2, while the trivial fixed
point with a flat interface is stable, the flow diverges for large
¯
λ and hence we
anticipate a rough-smooth transition for some characteristic value of
¯
λ. The upper
critical dimension for the problem would be one for which the rough phase would
cease to exist.
