Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

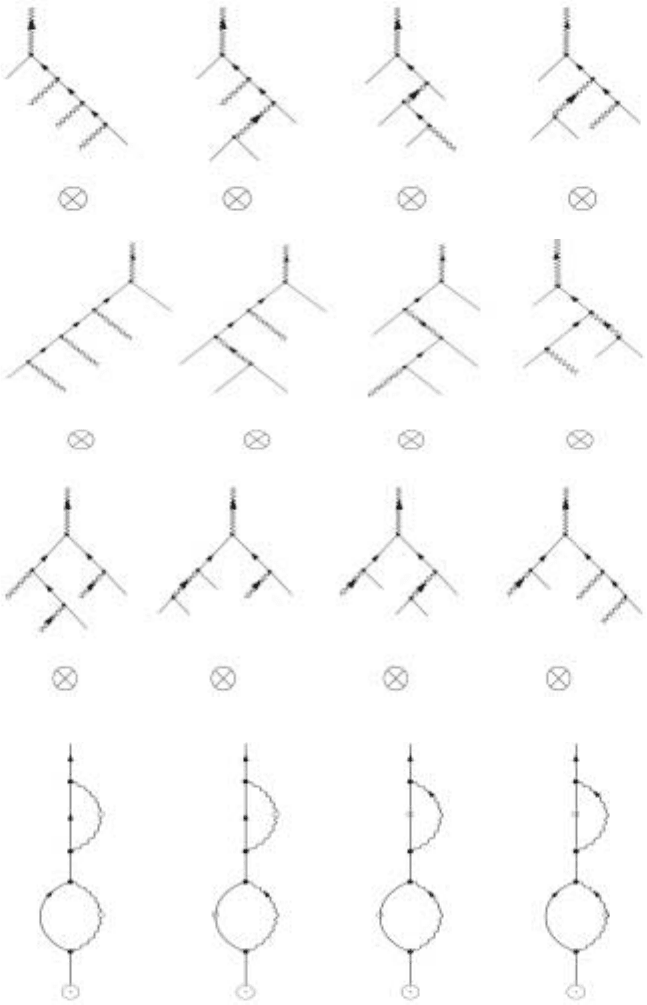
5.4 Diagrammatic Perturbation Theory 121

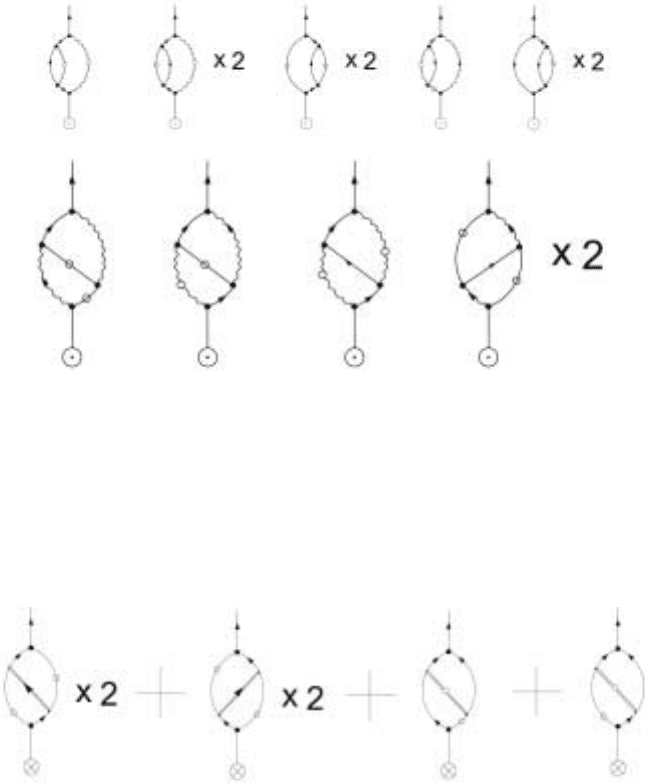
122 5 Critical Dynamics in Fluids

Figure 5.5. The two loop response function for the order parameter

be handled by dressing the lines involved in the single loop graphs. The diagrams

in third row of Fig. 5.5 constitute the vertex correction diagrams and are in some

sense the genuine two-loop diagrams. The vertex correction contributions to the

fourth order velocity response function are shown in Fig. 5.6. The reader should

write down the algebraic expressions corresponding to the ﬁgures.

Figure 5.6. The two loop response function for the velocity

5.5 Self-Consistent Perturbation Theory

We now use the self consistent perturbation theory to determine the critical be-

haviour. To do the self consistent calculation with Eqns.(5.3.24) and (5.3.28), we

replace the bare response and correlation functions by the full response and corre-

lations functions. Further we assume that the nonlinear contributions 

and 

5.5 Self-Consistent Perturbation Theory 123

to the relaxation rates dominate the bare relaxation rates λ(k

+κ

and ηk

Thus

−1

=−iω +

(k,κ,ω) (5.5.1)

−1

=−iω +

(k,κ,ω) (5.5.2)



= k

+κ

)



(2π)

dω



2π

sin

+κ

(k −p, ω −ω



)

×G

(p, ω



) (5.5.3)



(k,κ,ω) =

2(D −1)



(2π)

dω



2π

sin

+κ

−( p −



]

[κ



k −p)

]

×G

(p, ω



(k −p, ω −ω



) (5.5.4)

The self consistent set of equations for the problem are provided by Eqns.(5.5.1)-

(5.5.4). With the scaling Ansatz



+κ

−X



4−X



(5.5.5)



−X



4−X



(5.5.6)

a simple power counting of Eq.(5.5.4) gives

=4 −D = (5.5.7)

It should be apparent from Eqns.(5.5.5) and (5.5.6) that our nonlinear contributions



and 

to the relaxation rates will dominate the non-critical contributions

λ(k

+κ

and ηk

if X

and X

are positive. This implies from Eq.(5.5.7), that

the critical ﬂuctuations will dominate for >0 i.e. D<4 i.e. in spatial dimensions

less than four. For D>4, the nonlinear contributions are irrelevant in the non-

longwavelength limit and the mean ﬁeld results are valid.

For the purpose of doing the frequency integration in Eqns.(5.5.3) and (5.5.4),

we assume the response functions to be Lorentzian i.e.

G(k,κ,ω)=−iω +(k,κ)

124 5 Critical Dynamics in Fluids

and that leads to



(k,κ,ω)=k

+κ

)



(2π)

sin

+κ

−iω +

(p, κ) +

(k −p, κ)

(5.5.8)

and



(k,κ,ω) =

2(D −1)



(2π)

sin

+κ

−(



k −p)

]

[( p −



+κ

]

−iω +

(p, κ) +

(k −p, κ)

(5.5.9)

We are now in a position to get the self consistent value of X

and X

. To do this,

we can afford to work at the critical point i.e. κ =0. In this limit, 

∼k

4−X

and 

∼k

2−X

and clearly for low k (the long wavelength limit, in which we are

interested), 



(for all D>2). It should also be pointed out here that when

the dependence on the external frequency ω is considered, these frequencies are

of the order of the relaxation rate of the order parameter and we will always have

ω 

. Writing Eqns.(5.5.8) and (5.5.9) in the limit κ →0, ω →0,



(k) =k



(2π)

sin



(k −p)

(5.5.10)



(k) =

2(D −1)



(2π)

sin

( p −



−(



k −p)

]

[

(p) +

(k −p)]

(5.5.11)

Writing



=

4−X

(5.5.12)



=

2−X

(5.5.13)

Eq.(5.5.10) yields



= k



(2π)

sin

(



k −p)

2−X



(2π)

sin

(



1 −p)

2−X

=I(X

) (5.5.14)

5.5 Self-Consistent Perturbation Theory 125

while Eq.(5.5.11) yields



−2

2(D −1)



(2π)

sin

( p −



−(



k −p)

]

4−X



k −p|

4−X

]

2(D −1)



(2π)

sin

(



1 −p)

−(



k −p)

]

4−X



1 −p|

4−X

]

=J(X

) (5.5.15)

where all momenta have been scaled by k. The equality,

I(X

) =J(X

) (5.5.16)

following from Eqns.(5.5.14) and (5.5.15) yields the exponent X

and from

Eq.(5.5.7) the exponent X

At this point we will carry out an approximation. If D 4, i.e.  0, then both

and X

are small, and assuming that both exponents are O(), we note that

both the integrals I and J have poles at  =0. The contribution to the pole comes

from the momenta p 1 and we have

I(X

) 

(2π)





sin

4−X

where

2π

D/2

(D/2)

is the surface area of the D-dimensional sphere. Noting that the average of cos

in D-dimensional space is D

−1

,wehave

I(X

) 

(2π)



1 −







1+−X

(2π)



1 −



 −X

(5.5.17)

In the same limit

J(X

) 

2(D −1)

(2π)



sin

θ cos

4−X

(2π)

D −1

D +2



1 −



 −X



(2π)



1 −



(5.5.18)

126 5 Critical Dynamics in Fluids

Equating, according to Eq.(5.5.16)



+O(

) (5.5.19)

18

+O(

) (5.5.20)

Hence the interesting physical result that for D<4, the transport coefﬁcient λ and

the shear viscosity η diverge as the critical point is approached. scaling implies that

if we are in the long wavelength limit (i.e. k 0) and approach the critical point

(i.e. start from ﬁnite κ and approach κ =0), then the excess transport coefﬁcient

λ and the excess shear viscosity η coming from the critical ﬂuctuations behave

λ ∼ ξ

(5.5.21)

η ∼ ξ

(5.5.22)

where ξ is the correlation length.

It should be noted that the divergence of the shear viscosity is weak (X



for  1) and often it is a good approximation to set X

=0 to ﬁnd the concentra-

tion transport coefﬁcient λ. If this is done then Eq.(5.5.8) yields in the physical

dimension D =3

λ(k, κ) =



(2π)

sin

+κ



(k, κ)



(2π)

sin

+κ

(



k −p)

(5.5.23)

In the limit κ =0

λ =

ηk



(2π)

sin

(



1 −p)

ηk

4π

(2π)

(5.5.24)

while in the limit k =0,

λ =

4π

(2π)



4π

sin

1 +p

4π

(2π)

6πηκ

(5.5.25)

For arbitrary k and κ, the integral in Eq.(5.5.23) can be done exactly and we have

λ(k, κ) =

6πηκ

K(kξ) (5.5.26)

5.6 Sound Propagation 127

where

K(x)=



1 +x



−



tan

−1



(5.5.27)

is generally known as the Kawasaki function.

What we have thus far described is the dynamic critical behaviour of the con-

centration ﬂuctuations and velocity ﬂuctuations in binary liquids. The ordinary

ﬂuid near the liquid-vapour critical point is in the same universality class but as

we have discussed before the order parameter for the liquid-vapour critical point

is not a clear density ﬂuctuation but a mixture of density and energy ﬂuctuations -

in fact it is very close to the entropy ﬂuctuations. Consequently, in Eq.(5.2.1), ψ

stands for the entropy ﬂuctuations and λ is the thermal conductivity and χ denotes

the speciﬁc heat at constant pressure. The coupling to the velocity ﬂuctuations and

the nonlinearity in the velocity equation remain unaltered and Eqns.(5.5.21) and

(5.5.22) imply that the thermal conductivity and shear viscosity diverge near the

liquid-vapour critical point.

5.6 Sound Propagation

The three basic dissipative processes in a ﬂuid have to do with thermal conductivity,

shear viscosity and bulk viscosity. The ﬁrst two have been dealt with - the third

has to do with sound propagation. Sound waves are the propagation of density

ﬂuctuations in the system. The density ﬂuctuations are directly related to the order

parameter ﬂuctuations for the liquid vapour critical point and only indirectly related

for the binary liquid critical point. As the critical point is approached the order

parameter ﬂuctuations become extremely prominent and absorb energy from wave

- this makes the propagation of low frequency sound waves impossible near the

critical point. To see this, let us write down the hydrodynamic equations giving the

propagation of sound waves. The hydrodynamic equations are,

∂ρ

∂t

∂

∂x

(ρv

) =0 (5.6.1)

∂

∂t

(ρv

) +

∂

∂x

(ρv

) =−

∂P

∂x

(5.6.2)

∂

∂t

(ρs) +

∂

∂x

(ρsv

) =0 (5.6.3)

where s is entropy per unit mass. The equilibrium density, temperature, entropy

and pressure are denoted by ρ

and P

. The equilibrium velocity is zero.

The ﬂuctuations in ρ,T,s and P are δρ , δT , δs and δP. We linearize Eqns.(5.6.1)-

(5.6.3) in these variables and v which is already a ﬂuctuation.

128 5 Critical Dynamics in Fluids

∂

∂t

δρ +

∂

∂x

(ρ

) = 0 (5.6.4)

∂

∂t

(ρ

) =−

∂

∂x

δP (5.6.5)

∂

∂t

(δρ) +

∂

∂t

(ρ

δs) +

∂

∂x

(ρ

) = 0 (5.6.6)

Using Eq.(5.6.4), we can reduce Eq.(5.6.6) to

∂

∂t

δs =0 (5.6.7)

In the absence of dissipation, the entropy is constant and thus the process is isen-

tropic. We choose δρ and δT as our independent variables and write

δs =

∂s

∂ρ



δρ +

∂s

∂T



δT (5.6.8)

δP =

∂P

∂ρ



δρ +

δP

δT



δT (5.6.9)

We can take the constant value of δs to be at its initial value which is zero and

hence Eq.(5.6.8) leads to

δT =−

∂T

∂ρ



δρ (5.6.10)

We can now write Eq.(5.6.5) as

0 = ρ

∂v

∂t

∂

∂x



∂P

∂ρ



δρ +

δP

δT



δT



= ρ

∂v

∂t

∂

∂x



∂P

∂ρ



δP

δT



∂T

∂ρ





δρ

= ρ

∂v

∂t

∂

∂x



∂P

∂ρ



δρ



= ρ

∂v

∂t

∂P

∂ρ



∂

∂x

δρ (5.6.11)

A time derivative takes us to

∂

∂t

=−

∂P

∂ρ



∂

∂x

∂

∂t

δρ

∂P

∂ρ



∂

∂x

∂

∂x

∂P

∂ρ



∂

∂x

(5.6.12)

5.6 Sound Propagation 129

where in the last line we have used the fact that in the linearized equations, the

velocity ﬁeld is curl free. Thus

∂

∂t

∂P

∂ρ



∇

(5.6.13)

and we have a wave propagation with speed v

given by

∂P

∂ρ



(5.6.14)

We now show that near the critical point, the response

∂P

∂ρ

)

vanishes weakly. The

vanishing shows the impossibility of sound propagation in a critical ﬂuid. One can

write

∂P

∂ρ



∂P

∂ρ



∂P

∂T



∂T

∂ρ





∂P

∂T



∂T

∂ρ



(5.6.15)

near the critical point, since the isothermal response

∂ρ

∂P



diverges strongly near

the critical point. Further,

∂P

∂ρ





∂P

∂T



∂T

∂ρ



=−

∂P

∂T



∂T

∂s



∂s

∂ρ



∂P

∂T



∂s

∂V





∂s

∂T





∂P

∂T





(5.6.16)

The derivative

∂P

∂T

)

is non critical. The constant volume speciﬁc heat has a weak

divergence C

∼ξ

α/ν

, and thus the velocity has a weak zero in the zero frequency

limit.

The sound propagation occurs at ﬁnite frequencies and thus the response func-

tion C

does not actually diverge. So long as the relaxation time of the critical

ﬂuctuations, which is proportional to ξ

is shorter than ω

−1

, where ω is the fre-

quency of the sound wave, the speciﬁc heat C

behaves as the zero frequency

response should i.e. C

∼ξ

α/ν

. Once ξ

∼

, C

∼(

)

α/zν

and if the temperature

is brought closer to the critical point i.e. ξ increases, the system cannot respond any

more and the speciﬁc heat remains at ω

−α/zν

. This means that for a sound wave of

frequency ω, the propagation velocity decreases as the liquid vapour critical point

is approached and reaches a minimum at the critical point. The minimum is lower,

the lower the frequency of the sound wave.

130 5 Critical Dynamics in Fluids

The speciﬁc heat is a response function and hence the frequency dependence

is determined by the combination −iω. This means that the velocity given by

Eq.(5.6.16) is going to be complex , which is exactly as it should be since energy

from the sound wave will be transferred to the critical ﬂuctuations. The plane wave

(in one dimension e.g.) is given by e

ikx

, where the wave number k =ω/u, and

where u is the sound speed. Dissipation corresponds to k having an imaginary part

since a damped wave is written as e

ikx−bx

. Thus the wave number k for a sound

wave with dissipation is complex and follows from a complex sound speed. The

relation between complex sound speed and wave number is

+ik

)

+iu

)



−

2iu

(5.6.17)

giving

= k

−k

k

and

=−

(5.6.18)

The complex sound speed near the liquid vapour critical point can be written as

(5.6.19)

Where C

is a noncritical constant and C

is the response function which is sensitive

to the temperature difference from the critical point and the frequency. For ξ



−1

the zero frequency speciﬁc heat has the usual form

∝ξ

α/ν

=A(ξ

)

α/ν

+B (5.6.20)

where B is a noncritical constant. For ξ



, the response ﬁxed at its value for

∼

and hence the frequency dependent speciﬁc heat at T =T

, i.e. ξ =∞,is



−iω



α/zν

+B (5.6.21)

the i coming from the causal nature of the response function (Kramers-Kronig

relation). The velocity can be written as

−2



(−iω)

−α/zν





α/zν

(cos

απ

2zν

+i sin)

απ

2zν



From Eq.(5.6.18)