Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.

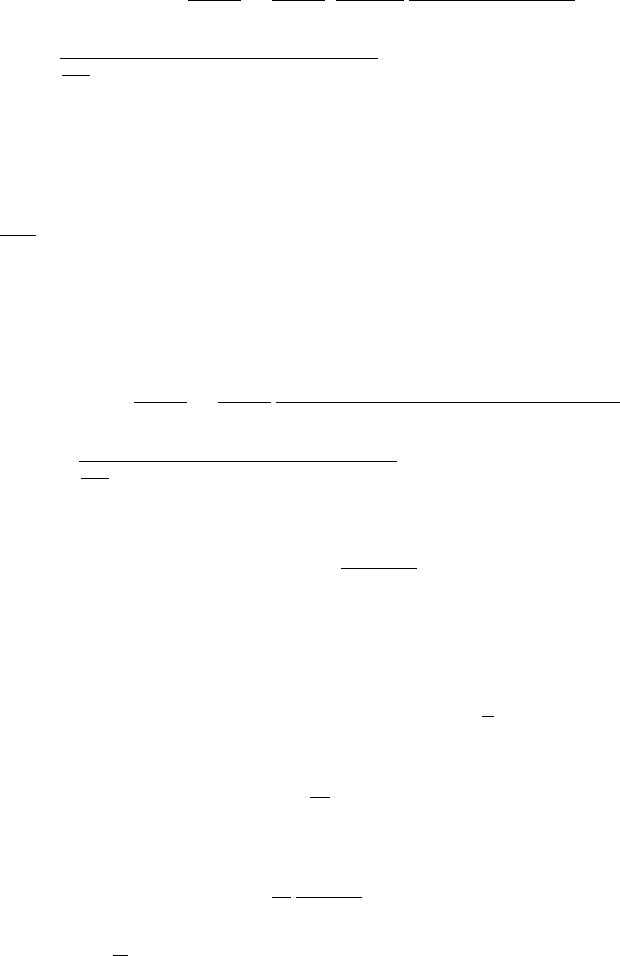
3.3 Dynamics of Model A 71
We can write the above term as
6λ
2
φ
<
(
k, ω)
d
D
p
1
(2π)
D
d
D
p
2
(2π)
D
1
p
2
2
+m
2
1
(
k −p
1
−p
2
)
2
+m
2
×
1
−iω
+p
2
1
+p
2
2
+(
k −p
1
−p
2
)
2
+3m
2
The eighth and ninth terms on the R.H.S of Eq.(3.3.18), when treated in the same
manner yield terms similar to the above with p exchanging places with p
1
in one
and
k −p
1
−p
2
in the other. We can now write the effective equation of motion
for φ
<
as
[
−iω
+k
2
+m
2
−(k,ω)]φ
<
(k, ω) =−λ
φ
<
( p
1
,ω
1
)φ
<
( p
2
,ω
2
)
× φ
<
(
k −p
1
−p
2
,ω−ω
1
−ω
2
) +N
<
(3.3.25)
where the “self-energy” (k,ω) is given by
(k, ω) = 6λ
2
d
D
p
1
(2π)
D
d
D
p
2
(2π)
D
p
2
1
+p
2
2
+(
k −p
1
−p
2
)
2
+3m
2
(p
2
1
+m
2
)(p
2
2
+m
2
)[(
k −p
1
−p
2
)
2
+m
2
]
×
1
−iω
+p
2
1
+p
2
2
+(
k −p
1
−p
2
)
2
+3m
2
(3.3.26)
We can expand the above self-energy as
(k, ω)=(k, 0) +(−iω)
∂(k, ω)
∂(−iω)
0
+...... (3.3.27)
The first term gives a contribution to the statics. The statics with the quartic in-
teraction showed us in §3.2, that the quartic interaction is relevant for D<4 and
thus inspires a perturbation theory in =4 −D and to the lowest order in , this
means the integrals like the one shown in Eq.(3.3.26) need to be evaluated at D =4.
Keeping in mind that the momentum integration runs between
b
and , one gets
(k, 0) =−ηk
2
lnb, where the anomalous dimension exponent
η =
2
54
(3.3.28)
for a general value of n, the this answer is
η =
2
2
n +2
(n +8)
2
.
In deriving η =
2
54
, we need the fixed point value of λ. This is obtained from
statics. The renormalization of ‘m’ and ‘λ’ that come from the purely static part
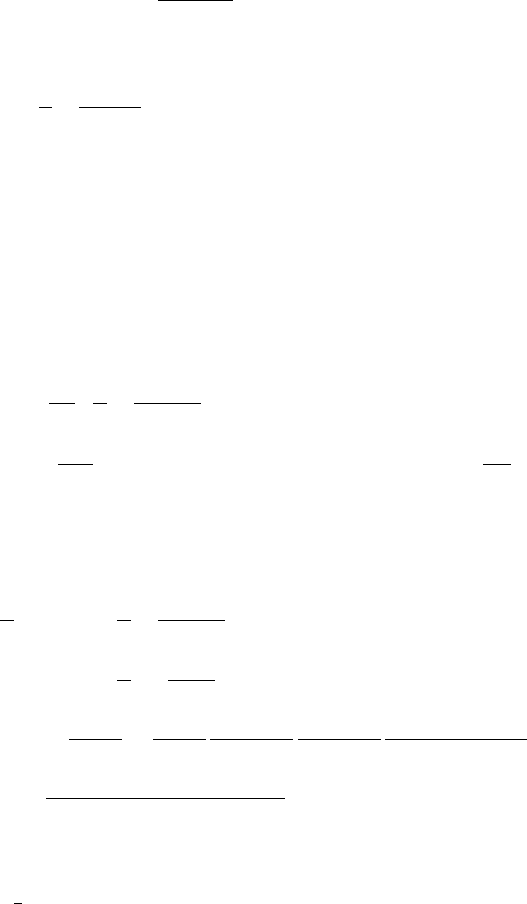
72 3 The Renormalization Group
give transformation equations for these couplings which for D<4 support a non-
Gaussian fixed point. The appropriate fixed point value λ
∗
of λ, when used in
Eq.(3.3.26) gives
∂(k, ω)
∂k
2
ω=k=0
=−ηlnb (3.3.29)
with η prescribed by Eq.(3.3.28). The equation of motion for φ
<
now reads
−iω
1
−
∂
∂(−iω)
ω=k=0
+ k
2
(1 +η lnb) +˜m
2
φ
<
=−λ
φ
<
( p
1
)φ
<
( p
2
)φ
<
(
k −p
1
−p
2
)
(3.3.30)
We now carry out the nest two steps in the RGT
• i) the momenta are scaled to k
=bk, and frequency to ω
=b
z
ω to restore the
cutoff to and and
• ii) The field φ
<
is rescaled to φ
<
ζ , so that the coefficient of k
2
is unchanged.
This now gives us the equation of motion as
−
iω
b
z
1
−
∂
∂(−iω
)
ω
=k=0
+
k
2
ζ
b
2
(1 +η lnb) +˜m
2
ζ
φ
<
=−λ
ζ
3
φ
<
φ
<
φ
<
+
N
<
(3.3.31)
The requirement of the coefficient of k
2
be unity fixes ζ =b
2−η
. The relaxation
rate is seen to be renormalized to
1
= b
2−η−z
1
−
∂
∂(−iω
)
ω
=k=0
= b
2−η−z
1
+6
λ
∗
2
b
z
b
z
×
d
D
p
1
(2π)
D
d
D
p
2
(2π)
D
1
(p
2
1
+m
2
)
1
(p
2
2
+m
2
)
1
( p
1
+p
2
)
2
+m
2
)
×
1
p
2
1
+p
2
2
+( p
1
+p
2
)
2
+3m
2
)
(3.3.32)
The integral needs to be evaluated at D =4, since λ
∗
is already O() and stan-
dard techniques of doing such integrals (note that the momentum integrations are
between
λ
b
and λ and in this high momentum range m
2
can be dropped) leads to
(power counting shows a logarithmic divergence)

3.4 Inclusion of Reversible Terms 73
1
=
b
2−η−z
1 +6ηln
4
3
lnb
=
1
1 +{
6 ln
4
3
η +
2 −η −z
} lnb +......
(3.3.33)
The fixed point of the relaxation rate leads to
z =2 +(6 ln
4
3
−1)η +O(
3
) (3.3.34)
Thus in model A, the nontrivial dynamic exponent is determined to O(
2
).We
have demonstrated this calculation in great detail because this is the way all the
dynamic renormalization group (DRG) calculations can be done.
For model B, an identical calculation can be carried out. However, as should
be explicitly verified by the reader, the integral
∂
∂(−iω)
k,ω=0
in this case does not show the logarithmic divergence shown in the first step of
Eq.(3.3.33) and consequently, for the model with the conservation law z =4 −η.
3.4 Inclusion of Reversible Terms
This section will be devoted to studying the operation of RG on the reversible
nonlinear part in the equation of motion. We will takeas our example theHeisenberg
ferromagnet, where the equation of motion is given in Eq.(2.4.11), which we now
write in momentum space,
˙
φ
i
(k, t) = g
p
1
+p
2
=
k
ilm
(p
2
−p
2
)φ
l
( p)φ
m
( p
) −k
2
(k
2
+m
2
)φ
i
(k)
− λk
2
p
1
, p
2
[φ
j
( p
1
)φ
j
( p
2
)]φ
i
(
k −p
1
−p
2
) +N
i
(3.4.1)
In the first term
ilm
is the Levi Civita symbol which is zero if any of the two
indices are equal and
123
=1. One permutation of the subscripts changes the sign.
It should be noted that there are two kinds of nonlinear terms in the above equation.
• i) the dissipative kind with coupling constant λ which we have
already dealt with
• ii) the reversible term with coupling constant g which ensures
d
dt
[φ
i
(k)φ
i
(−k)]=0

74 3 The Renormalization Group
From our previous discussion, we know that the coupling constant λ is relevant for
D<4. The first issue that we need to determine is when is the coupling constant
g relevant? For this discussion, we need not consider the λ term and we have the
equation of motion
−
iω
/χ
+k
2
φ
1
(k, ω) =
g
/χ
ω
1
+ω
2
=ω
p
1
+p
2
=
k
φ
2
( p
1
,ω
1
)φ
3
( p
2
,ω
2
)(p
2
1
−p
2
2
) +
N
/χ
(3.4.2)
As the detailed calculations of the previous section show, removing the fast vari-
ables produces produces an effective equation of motion for the slow variables. We
are not interested in all the different terms, right now we want to concentrate on
one term term which is guaranteed to be there, which makes the effective equation
of motion
−
iω
/χ
+k
2
φ
<
1
(k, ω) =
g
/χ
φ
<
2
( p
1
,ω
1
)φ
<
3
( p
2
,ω
2
)(p
2
1
−p
2
2
) +
N
<
/χ
(3.4.3)
Doing the rescalings k
=bk, ω
=b
z
ω and φ
<
=ζφ
<
,wehave
−
iω
b
z−2
k
2
/χ
+1
φ
<
1
(k, ω) =
g
/χ
ζ
k
2
1
b
D+z
(p
1
2
−p
2
2
)
× φ
<
2
(
p
1
,ω
1
)φ
<
3
(
p
2
,ω
2
) +
N
<
/ζ
/χ
(3.4.4)
We need to choose ζ to be consistent with the states and hence with χ =χ
b
2
ζ =b
1+
D
2
+z
(3.4.5)
Rewriting Eq.(3.4.4) in the form
[−
iω
k
2
/χ
+1]φ
<
1
=
g
k
2
/χ
b
z−4
b
3−
D
2
(p
1
2
−p
2
2
)
×φ
<
2
φ
<
3
+
N
<
=
g
/χ
(p
2
1
−p
2
2
)φ
<
2
(p
1
)φ
<
3
(p
2
) +
N
where
=b
z−4
(3.4.6)
g
=gb
z−1−
D
2
(3.4.7)

3.4 Inclusion of Reversible Terms 75
At the fixed point for , z =4 and we have
g
=gb
6−D
(3.4.8)
The reversible term is relevant for D<6 and irrelevant for D>6. Consequently,
for D>6, the reversible term has no effect on the dynamics i.e. z =4 will be exact.
For D<6, the reversible will change the value of z and this is what we now turn to.
We now proceed to carry out the RGT as done in the previous section for the
dissipative model and write (i, j and k are always cyclic in 1, 2, 3)
−
iω
+k
2
(k
2
+m
2
)
φ
<
i
(k, ω) =
g
(p
2
1
−p
2
2
)φ
<
j
( p
1
)φ
<
k
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
<
j
( p
1
)φ
>
k
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
>
j
( p
1
)φ
<
k
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
>
j
( p
1
)φ
>
k
( p
2
) +
N
<
(3.4.9)
and
−
iω
+k
2
(k
2
+m
2
)
φ
>
1
(k, ω) =
g
(p
2
1
−p
2
2
)φ
<
2
( p
1
)φ
<
3
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
>
2
( p
1
)φ
<
3
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
<
2
( p
1
)φ
>
3
( p
2
)
+
g
(p
2
1
−p
2
2
)φ
>
2
( p
1
)φ
>
3
( p
2
) +
N
>
(3.4.10)
As before, one is expected to solve for φ
>
and insert the result in Eq.(3.4.9) to
obtain the effective equation of motion for φ
<
. To solve for φ
>
perturbatively we
expand
φ
>
i
=φ
>(0)
i
+
g
φ
>(1)
i
+..
with
[−
iω
+k
2
(k
2
+m
2
)]φ
>(0)
1
=
N
>
(3.4.11)
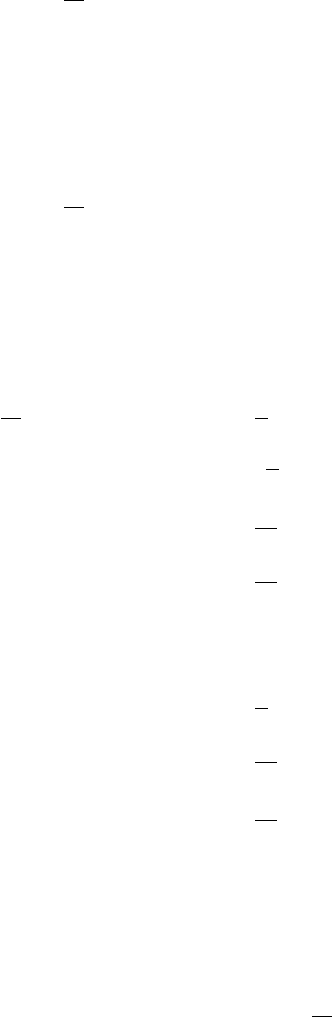
76 3 The Renormalization Group
[−
iω
+k
2
(k
2
+m
2
)]φ
>(1)
1
=
(p
2
1
−p
2
2
)φ
<
2
( p
1
)φ
<
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
>(0)
2
( p
1
)φ
<
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
<
2
( p
1
)φ
>(0)
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
>(0)
2
( p
1
)φ
>(0)
3
( p
2
) (3.4.12)
and
[−
iω
+k
2
(k
2
+m
2
)]φ
>(2)
1
=
(p
2
1
−p
2
2
)φ
>(1)
2
( p
1
)φ
<
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
<
2
( p
1
)φ
>(1)
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
>(0)
2
( p
1
)φ
>(1)
3
( p
2
)
+
(p
2
1
−p
2
2
)φ
>(1)
2
( p
1
)φ
>(0)
3
( p
2
) (3.4.13)
Inserting the power series expansion of φ
>
in Eq.(3.4.9), we get
[−
iω
+k
2
(k
2
+m
2
)]φ
<
1
(k, ω) =
g
(p
2
1
−p
2
2
)φ
<
2
( p
1
,ω
1
)φ
<
3
( p
2
,ω
2
)
+
g
(p
2
1
−p
2
2
)φ
<
2
( p
1
,ω
1
)φ
>(0)
3
( p
2
,ω
2
)
+
g
2
2
(p
2
1
−p
2
2
)φ
<
2
( p
1
,ω
1
)φ
>(1)
3
( p
2
,ω
2
)
+
g
3
3
(p
2
1
−p
2
2
)φ
<
2
( p
1
,ω
1
)φ
>(2)
3
( p
2
,ω
2
)
+ a similar term with subscripts 2 and 3
on φ interchanged
+
g
(p
2
1
−p
2
2
)φ
>(0)
2
( p
1
,ω
1
)φ
>(0)
3
( p
2
,ω
2
)
+
g
2
2
(p
2
1
−p
2
2
)
φ
>(1)
2
φ
>(0)
3
+φ
>(1)
3
φ
>(0)
2
+
g
3
3
(p
2
1
−p
2
2
)
φ
>(2)
2
φ
>(0)
3
+φ
>(2)
3
φ
>(0)
2
+ φ
>(1)
2
φ
>(1)
3
+..... (3.4.14)
The solution for φ
>(i)
1
can be written as
φ
>(0)
1
= GN
>
/
with G
−1
=−
iω
+k
2
(k
2
+m
2
) (3.4.15)

3.4 Inclusion of Reversible Terms 77
(Note that G is independent of the component φ
i
).
φ
>(1)
1
(k, ω) = G(k, ω)
(p
2
1
−p
2
2
)φ
<
2
( p
1
,ω
1
)φ
<
3
( p
2
,ω
2
)
+
(p
2
1
−p
2
2
)
φ
>(0)
2
( p
1
,ω
1
)φ
<
3
( p
2
,ω
2
)
+ φ
<
2
( p
1
,ω
1
)φ
>(0)
3
( p
2
,ω
2
) +φ
>(0)
2
( p
1
,ω
1
)φ
>(0)
3
( p
2
,ω
2
)
(3.4.16)
From the R.H.S of Eq.(3.4.14) we are supposed to find
• i) a term linear in φ
<
1
(k, ω) that will help renormalize
−1
and
• ii) a term of the form φ
<
2
φ
<
3
that will help renormalize the coupling constant g
To find the renormalization of , the correct terms on the R.H.S of Eq.(3.4.14) are
g
2
(p
2
1
−p
2
2
)
φ
>(1)
2
(p
1
)φ
>(0)
3
(p
2
) +φ
>(0)
(p
1
)φ
>(1)
3
(p
2
)
Looking at the first term of the above expression, we have
g
2
(p
2
1
−p
2
2
)φ
>(1)
2
(p
1
)φ
>(0)
3
(p
2
) =
g
2
(p
2
1
−p
2
2
)
G(p
1
,ω
1
)
×[q
2
−( p
1
−q)
2
]φ
<
1
(p
1
−q,ω
1
−ω
)
× φ
>(0)
3
(q, ω
)φ
>(0)
3
(p
2
,ω
2
)
Doing the averaging over the noise, it becomes
g
2
(p
2
1
−p
2
2
)[−q
2
+( p
1
−q)
2
]G(p
1
,ω
1
)φ
<
1
(q, ω
)
×
φ
>
3
(p
2
,ω
2
)φ
>
3
(−p
2
, −ω
2
)
δ(
k −q)δ(ω −ω
)
=φ
<
1
(k
ω)(
g
)
2
(p
2
1
−p
2
2
)(−k
2
+p
2
2
)
×
2
p
2
2
[
ω
2
2
2
+p
4
2
(p
2
2
+m
2
)
2
]
1
[−
iω
1
+p
2
1
(p
2
1
+m
2
)]
=φ
<
1
(k
ω)
g
2
(p
2
1
−p
2
2
)(k
2
−p
2
2
)
(p
2
2
+m
2
)
1
−
iω
+p
2
1
(p
2
1
+m
2
) +p
2
2
(p
2
2
+m
2
)
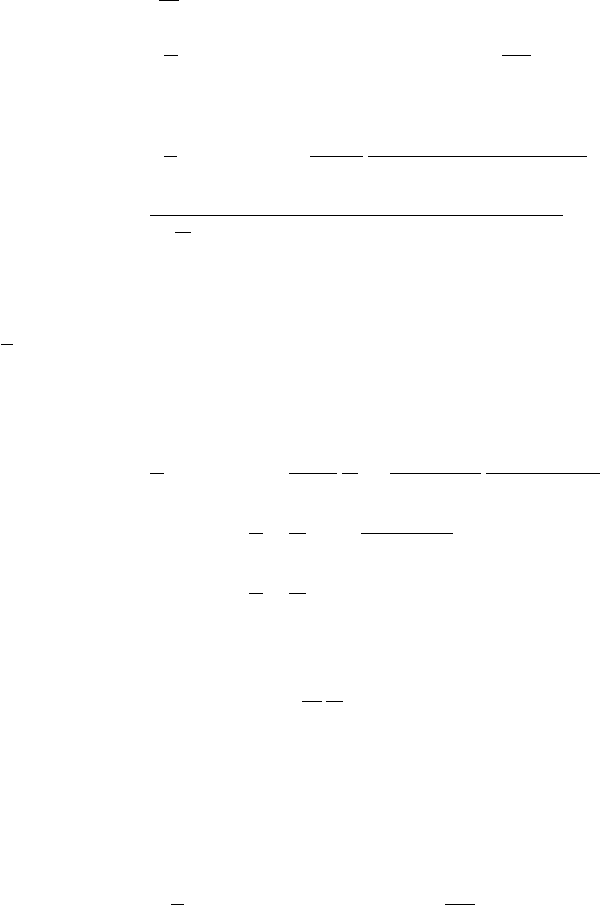
78 3 The Renormalization Group
The two terms together give
−
iω
+k
2
(k
2
+m
2
) +(k, ω)
φ
<
1
(k, ω) (3.4.17)
=
g
(p
2
1
−p
2
2
)φ
<
2
(p
1
,ω
1
)φ
<
2
(p
1
,ω
1
) +
N
<
(3.4.18)
where
(k, ω) =
g
2
(k
2
+m
2
)
d
D
p
1
(2π)
D
[p
2
1
−(
k −p
1
)
2
]
2
(p
2
1
+m
2
)[(
k −p
1
)
2
+m
2
]
×
1
[−
iω
+p
2
1
(p
2
1
+m
2
) +(
k −p
1
)
2
{(
k −p
1
)
2
+m
2
}]
(3.4.19)
Note that (k,ω) is dynamic in origin and unlike the dissipative case, does not
have any static component which has to be separated. This self-energy (k, ω)
renormalizes and we can carry out the momentum integration over p such that
b
<p<. In this high momentum region, the integral has a logarithmic diver-
gence at D =6, which is the upper critical dimension, i.e. where g becomes rele-
vant. We evaluate the integral in D =6, to find (one needs to remember that p is
large and appropriate approximations are necessary)
(k, ω) =
g
2
(k
2
+m
2
)k
2
C
6
(2π)
6
4
D
p
5
dp
(p
2
+m
2
)
2
p
2
2p
2
(p
2
+m
2
)
= k
2
(k
2
+m
2
)
g
2
2
D
K
6
p
5
dp
(p
2
+m
2
)
3
= k
2
(k
2
+m
2
)
g
2
2
D
K
6
lnb (3.4.20)
Looking back at Eq.(3.4.17) and multiplying by we can identify
=
g
2
2
D
K
6
lnb (3.4.21)
To find the renormalization of the coupling constant g, we need to look at the
last group of terms (involving g
3
/
3
) in the R.H.S of Eq.(3.4.14) and we use
φ
>(2)
i
from the first two terms of the R.H.S of Eq.(3.4.13), with φ
>(1)
i
coming from
the second and third terms on the R.H.S of Eq.(3.4.16). We then generate all the
non-zero terms (after averaging over φ
>(0)
i
), of the form
g
(p
2
1
−p
2
2
)φ
<
j
( p
1
)φ
<
k
( p
2
) +
N
<
and the sum of the three contributing terms add upto zero. Hence, to this order, g
is not renormalized.

3.5 Field Theoretic Form 79
Returning to Eq.(3.4.7) the fact that g is not normalized leads to the relation
z =1 +
D
2
(3.4.22)
For D<6, z<4 and that implies the Onsager coefficient has to diverge for D<6
which is represented by the scaling of Eq.(3.4.6) and we have
= b
z−4
=b
D
2
−3
=b
−
2
=
1 −
2
ln b +O(
2
)
(3.4.23)
Adding in the contribution from Eq.(3.4.20) we find
= +
−
2
+
2
6
g
2
2
K
6
ln b (3.4.24)
The fixed point is reached for
g
2
2
=
3
2 K
6
=96π
3
(3.4.25)
which is a universal number (dependent only on dimensionality of space). The
Onsager coefficient thus diverges as k
−/2
and >0 i.e. D<6, and has an
amplitude
0
such that the number g
2
/
2
0
is an universal number. Thus, in the
dynamics, we can have universal exponents and universal amplitude combinations.
In the above discussion, calculations have been carried out to O(). The non-
renormalizability of the coupling constant ‘g’ is however correct to all orders in
and thus the conclusion z =1 +
D
2
is exact. However, in getting this answer, η
has been ignored. For 6 >D>4, this does not matter since in that range η =0.
However, for D<4, there will be O(η)correction to the dynamic scaling exponent.
By going through the detailed calculation for the dissipative coupling and the
reversible coupling, we have covered all possible ways in RG techniques that one
uses in dynamics.
3.5 Field Theoretic Form
In this section, we give a very sketchy indication of how the dynamics problem can
be made to look very much like a problem in statics and the field theoretic methods
of statics can be brought to bear to solve it. We do this first for the simplest system
- linearized version of model A. The equation of motion is,
∂φ(
k)
∂t
=−(k
2
+m
2
)φ(k) +N(k,t) (3.5.1)
80 3 The Renormalization Group
with
N(k
1
,t
1
)N(k
2
,t)=2δ(
k
1
+
k
2
)δ(t
1
−t
2
) (3.5.2)
In frequency space,
[−iω +(k
2
+m
2
)]φ(k,ω) = N(k,ω)
N(k
1
,ω
1
)N(k
2
,ω
2
)=2δ(
k
1
+
k
2
)δ(ω
1
+ω
2
) (3.5.3)
The solution to the problem implies complete specification of the Green’s func-
tion G(k, ω) and the correlation function C(k,ω). The results for the model of
Eq.(3.5.3) are
G(k, ω) =
δφ(k
1
,ω
1
)
δN(k
2
,ω
2
)
1
δ(
k
1
+
k
2
)δ(ω
1
+ω
2
)
= (−
iω
+m
2
+k
2
)
−1
(3.5.4)
C(k,ω) =φ(k
1
,ω
1
)φ(k
2
,ω
2
)
1
δ(
k
1
+
k
2
)δ(ω
1
+ω
2
)
=
1
ω
2
2
+(k
2
+m
2
)
2
(3.5.5)
The probability distribution of the noise N is given by a Gaussian distribution
p(N) ∝exp[−
1
4
d
D
kdt |N(k,t)|
2
]
Instead of working with N(k,t), an equivalent description would be in terms
of φ(k,t) and
˙
φ(k, t) obtained by expressing N(k,t) in terms of them through
Eq.(3.5.1). It is even more convenient to introduce a set of auxiliary fields
˜
φ, not-
ing the result
e
−x
2
=
1
√
π
∞
−∞
d ˜xe
−˜x
2
−2ix ˜x
(3.5.6)
and write the probability distribution as a function of φ and
˜
φ in the form,
Z(φ,
˜
φ) ∼
D[φ]D[
˜
φ]e
−S(φ,
˜
φ)
(3.5.7)
where apart from a Jacobian S(φ,
˜
φ) is given in coordinate space by the expression
S(φ,
˜
φ) =
d
D
xdt[−
˜
φ
˜
φ +
˜
φ{
˙
φ +(m
2
−∇
2
)φ}] (3.5.8)
