Bhadeshia H.K.D.H., Honeycombe R. Steels: Microstructure and Properties

Подождите немного. Документ загружается.

48 CHAPTER 3 IRON–CARBON EQUILIBRIUM AND PLAIN CARBON STEELS

(a) (b)

Fig. 3.6 Phase diagram and its relationship to the concentration profile at the ferrite/austenite

interface during diffusion-controlled growth.

On combining these expressions to eliminate z we get:

∂z

∗

∂t

(

c −c

γα

)

∗

αγ

− c

γα

)(c

αγ

− c)

It follows that:

∗

(

c −c

γα

)

[2(c

αγ

− c

γα

)(c

αγ

− c)]



t. (3.2)

Consider now a ternary steel, say Fe–Mn–C. It would be necessary to satisfy two

equations of the form of Equation (3.1), simultaneously, for each of the solutes:

γα

− c

αγ

)v =−D

∇c

γα

− c

αγ

)v =−D

∇c



. (3.3)

Because D

≫D

, these equations cannot in general be simultaneously satis-

ﬁed for the tie-line passing through the alloy composition

, c

. It is, however,

possible to choose other tie lines which satisfy equation (3.3). If the tie-line is

such that c

γα

(e.g. line cd for alloy A of Fig. 3.7a), then ∇c

will become

very small, the driving force for carbon diffusion in effect being reduced, so that

the ﬂux of carbon atoms is forced to slow down to a rate consistent with the

diffusion of manganese. Ferrite forming by this mechanism is said to grow by

a ‘Partitioning, Local Equilibrium’ (or PLE) mechanism, in recognition of the

fact that c

αγ

can differ signiﬁcantly from

, giving considerable partitioning

and long-range diffusion of manganese into the austenite.

An alternative choice of tie-line could allow c

αγ

→

(e.g. line cd for

alloy B of Fig. 3.7b), so that ∇c

is drastically increased since only very small

amounts of Mn are partitioned into the austenite. The ﬂux of manganese atoms

at the interface correspondingly increases and manganese diffusion can then

keep pace with that of carbon, satisfying the mass conservation conditions of

Equation (3.3). The growth of ferrite in this manner is said to occur by a ‘Negli-

gible Partitioning, Local Equilibrium’ (or NPLE) mechanism, in recognition of

3.4 THE KINETICS OF THE γ → α TRANSFORMATION 49

(a)

(b)

Fig. 3.7 Schematic isothermal sections of the Fe–Mn–C system, illustrating ferrite growth

occurring with local equilibrium at the α/γ interface. (a) Growth at low supersaturations

(PLE) with bulk redistribution of manganese, (b) growth at high supersaturations (NPLE) with

negligible partitioning of manganese during transformation. The bulk alloy compositions are

designated by the symbol • in each case.

the fact that the manganese content of the ferrite approximately equals

,so

that little if any manganese partitions into austenite.

What circumstances determine whether growth follows the PLE or NPLE

mode? Figure 3.8 shows the Fe–Mn–C phase diagram, now divided into

domains where either PLE or NPLE is possible but not both. The domains

are obtained by drawing right-handed triangles on each tie-line in the α +γ

phase ﬁeld and joining up all the vertices. For example, if an attempt is made

50 CHAPTER 3 IRON–CARBON EQUILIBRIUM AND PLAIN CARBON STEELS

Fig. 3.8 Regions of the two-phase field where either PLE or NPLE modes of transformation

are possible.

Fig. 3.9 A para-equilibrium phase diagram.

to deﬁne NPLE conditions in the PLE domain, then the tie-line determining

interface compositions will incorrectly show that both austenite and ferrite

contain less carbon than

, a circumstance which is physically impossible.

Para-equilibrium is a constrained equilibrium. It occurs at temperatures

where the diffusion of substitutional solutes is not possible within the time scale

of the experiment. Nevertheless, interstitials may remain highly mobile. Thus,

in a steel, manganese does not partition between the ferrite and austenite, but

subject to that constraint, the carbon redistributes until it has the same chemical

potential in both phases.

Therefore, the tie lines in the phase diagram (Fig. 3.9) are all virtually parallel

to the carbon axis, since Mn does not partition between ferrite and austenite.

In an isothermal section of the ternary phase diagram, the para-equilibrium

phase boundaries must lie within the equilibrium phase boundaries as illustrated

in Fig. 3.10.

3.4 THE KINETICS OF THE γ → α TRANSFORMATION 51

(a) (b)

Fig. 3.10 The para-equilibrium phase field lies within the equilibrium field. The tie lines

illustrated are for equilibrium.

Fig. 3.11 (a) Plot of the parabolic thickening process described by Equation (3.1). (b) Interfacial

energies at the advancing edge of a ferrite allotriomorph (after Hillert, Jernkontorets Annaler

141, 757, 1957).

Since the thickness of an allotriomorph increases parabolically with time

(Fig. 3.11a), the growth rate decreases as the ferrite thickens. This is because

increasing quantities of carbon are rejected into the austenite as the ferrite

thickens, making the diffusion of carbon away from the transformation front

more difﬁcult.

Zener,and later Hillert, investigated theoretically the edgewise growth of an

allotriomorph with curved ends (Fig. 3.11b) assuming that the rate is controlled

by the diffusion of carbon in the austenite. The plate shape ensures that the

carbon rejected by the growing ferrite is distributed to the sides of the plates.

The carbon concentration proﬁle ahead of the plate tip therefore remains con-

stant as the plate lengthens. Consequently, unlike the thickening process, the

allotriomorphic ferrite lengthens at a constant rate G

= D

γα

−

′

(c −c

αγ

) sin 

, (3.4)

52 CHAPTER 3 IRON–CARBON EQUILIBRIUM AND PLAIN CARBON STEELS

where

′

=radius of curvature of the allotriomorph adjacent to the grain junction

(Fig. 3.11)

 =equilibrium growth angle determined by the relative energies of the

interphase and grain boundaries (Fig. 3.11).

The sin  term is present because each side of the allotriomorph makes an angle

 – π/2 with the γ/γ grain boundary (Fig. 3.11).

3.4.2 Growth kinetics of Widmanstätten ferrite

To apply Equation (3.4) to the growth of ferrite plates (Widmanstätten ferrite)

it is simply necessary to replace the term r

′

sin  by r, the radius of curvature

of the edge of the plate. More precise expressions for the growth rate G

can

be obtained by allowing for the variation of D

with carbon concentration

and temperature. In fact, for Widmanstätten ferrite, the lengthening rate goes

through a maximum as the radius of curvature of the plate increases (Fig. 3.12).

This is because a smaller tip radius allows the excess carbon to diffuse away

more rapidly, but a ﬁner radius also leads to an increased surface to volume

ratio, so that a greater proportion of energy has to be expended in creating the

surface. Zener argued that the plate would assume a radius consistent with the

maximum growth rate, and this is generally observed to be the case in practice.

Thickening studies on Widmanstätten ferrite plates using thermionic emis-

sion microscopy have shown that the process is irregular (Fig. 3.13). These

irregularities have been interpreted to imply that the thickening occurs by the

repeated migration of steps. Jones and Trivedi found that the velocity v of such

steps is given by:

v =

γα

−

δβ(c

γα

− c

αγ

)

, (3.5)

where δ is the step height, and β is a function of the velocity parameter

p =vδ/2D

. Notice that this equation cannot be applied unless the step height

is determined experimentally. An alternative interpretation of the irregular

growth is that the observations simply reﬂect the formation of new plates

adjacent to the original.

It is worth emphasizing that the growth of Widmanstätten ferrite is accom-

panied by a shape deformation which is an invariant-plane strain, frequently

involving the back-to-back growth of self-accommodating pairs of plates. This

gives an overall morphology which has the appearance of wedge shaped plates

emanating from the austenite grain surfaces. Therefore, Widmanstätten fer-

rite in alloy steels always grows by a para-equilibrium mechanism, without any

partitioning of substitutional solutes.

3.5 THE AUSTENITE–PEARLITE REACTION 53

Fig. 3.12 Variation in the plate lengthening rate as a function of its tip radius. r

is the critical

radius at which the lengthening rate becomes zero.

Fig. 3.13 Thickening of ferrite plates in an Fe–0.22C wt% alloy at 710

◦

C (Aaronson et al., in

Phase Transformations, ASM, USA, 1970).

3.5 THE AUSTENITE–PEARLITE REACTION

Pearlite is probably the most familiar microstructural feature in the whole sci-

ence of metallography (Figs 3.14a, b). It was discovered by Sorby over 120 years

ago, who correctly assumed it to be a lamellar mixture of iron and iron car-

bide. Pearlite is a very common constituent of a wide variety of steels, where

it provides a substantial contribution to strength, so it is not surprising that

this phase has received intensive study. Lamellar eutectoid structures of this

type are widespread in metallurgy, and frequently pearlite is used as a generic

54 CHAPTER 3 IRON–CARBON EQUILIBRIUM AND PLAIN CARBON STEELS

Fig. 3.14 Isothermal transformation of a 0.8C steel, 10 s at 650

◦

C. (a) Optical micrograph,

×80, (b) thin-foil electron micrograph of part of a pearlite nodule ×34,000 (courtesy of

Ohmori).

term to describe them. These structures have much in common with the cellular

precipitation reactions. Both types of reaction occur by nucleation and growth

(Fig.3.14a),and relyondiffusion. Pearlite nucleioccur onaustenite grain bound-

aries, but it is clear that they can also be associated with both pro-eutectoid

ferrite and cementite. In commercial steels, pearlite nodules can nucleate on

inclusions.

3.5.1 The morphology of pearlite

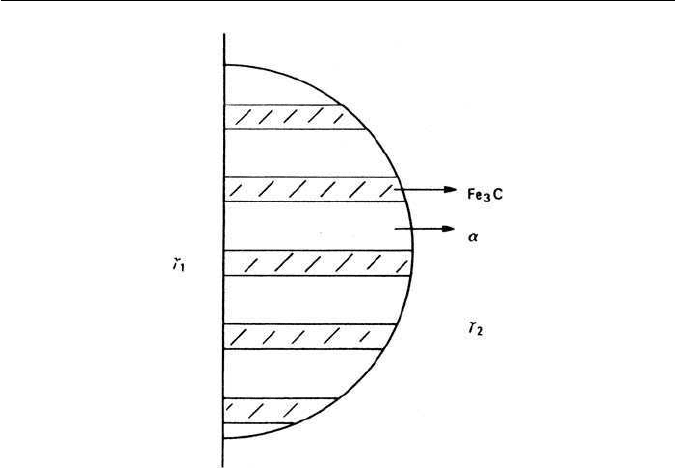
The idealized view of pearlite is a hemispherical nodule nucleated at an austen-

ite grain boundary, and growing gradually into one austenite grain (Fig. 3.15).

Apart from examining possible sites for nucleation, the following information

is needed:

(a) how the lamellae increase in number,

(b) the crystallographic relationships between the phases,

(d) the rate-controlling process.

Not all these questions can yet be fully answered, but the essentials are

established. Following the classical work of Mehl and colleagues, Hillert and

co-workers were able to show that pearlite could be nucleated either by ferrite,

or by cementite, depending on whether the steel was hypo- or hyper-eutectoid

in composition. They came to this conclusion after observing lattice continu-

ity between the ferrite in pearlite and pro-eutectoid ferrite, as well as between

cementite in pearlite and hyper-eutectoid cementite.

Mehl and co-workers took the view that pearlite nodules formed by side-

ways nucleation and edge-ways growth (Fig. 3.15). In this way,the rapid increase

3.5 THE AUSTENITE–PEARLITE REACTION 55

Fig. 3.15 Idealized pearlite nodule at austenite grain boundary.

in the number of lamellae in a nodule which occurred during growth could be

explained, but Modin indicated that this could equally well result from the

branching of lamellae during growth. Thin-foil electron microscopy work by

Dippenaar and Honeycombe on 13% Mn 0.8% carbon steel allowed the exam-

ination of very small nodules at an early stage of growth in an austenitic matrix

rendered stable by addition of manganese. This steel is hyper-eutectoid, so grain

boundary cementite forms prior to nucleation of pearlite which frequently takes

place on the cementite. This work showed conclusively the continuity of grain

boundary and pearlitic cementite (Fig. 3.16), and also indicated that both the

cementite and ferrite possessed unique orientations within a particular nodule.

Figure 3.16 also shows the beginning of branching of the Fe

C lamella. How-

ever, in other nodules, sideways nucleation of laths of cementite and ferrite

was observed. Nucleation of pearlite also took place on clean austenite bound-

aries. Hillert has shown that nucleation also occurs on ferrite, so all three types

of site are effective, and the predominant sites will be determined primarily

by the composition.

C. S. Smith ﬁrst pointed out that the moving pearlite interface in contact

with austenite was an incoherent high-energy interface growing into a grain

with which the pearlitic ferrite and cementite had no orientation relationship.

Therefore, the nodules which nucleated on pre-existing grain boundary cemen-

tite and ferrite would choose the higher energy interfaces across which the

boundary phase had no orientation relationship with the adjacent austenite.

56 CHAPTER 3 IRON–CARBON EQUILIBRIUM AND PLAIN CARBON STEELS

Fig. 3.16 Fe–13Mn–0.8C partly transformed at 600

◦

C. Austenite is retained in conjunction

with ferrite and cementite: (a) nucleation of a pearlite nodule on grain boundary cementite,

(b) interface of nodule with austenite. Thin-foil electron micrographs (courtesy of Dippenaar).

Hillert and co-workers were able to show by suitable heat treatments that

pearlite did nucleate in this way, while on the low-energy interfaces Wid-

manstätten growth of ferrite (or cementite) was usually observed. Electron

microscopy observations have conﬁrmed that the pearlite interface with austen-

ite is an incoherent one. Figure 3.16b shows a typical interface on a 13Mn–0.8C

wt% steel, where the untransformed austenite has been retained at room

temperature.

The spacing of the lamellae in pearlite is a sensitive parameter which, in a

particular steel,is larger the higher the transformation temperature.The spacing

was ﬁrst measured systematically for a number of steels by Mehl andco-workers,

whodemonstrated that thespacing decreasedas thedegree ofundercooling,T,

below the eutectoid temperature increased. Zener provided the ﬁrst theoretical

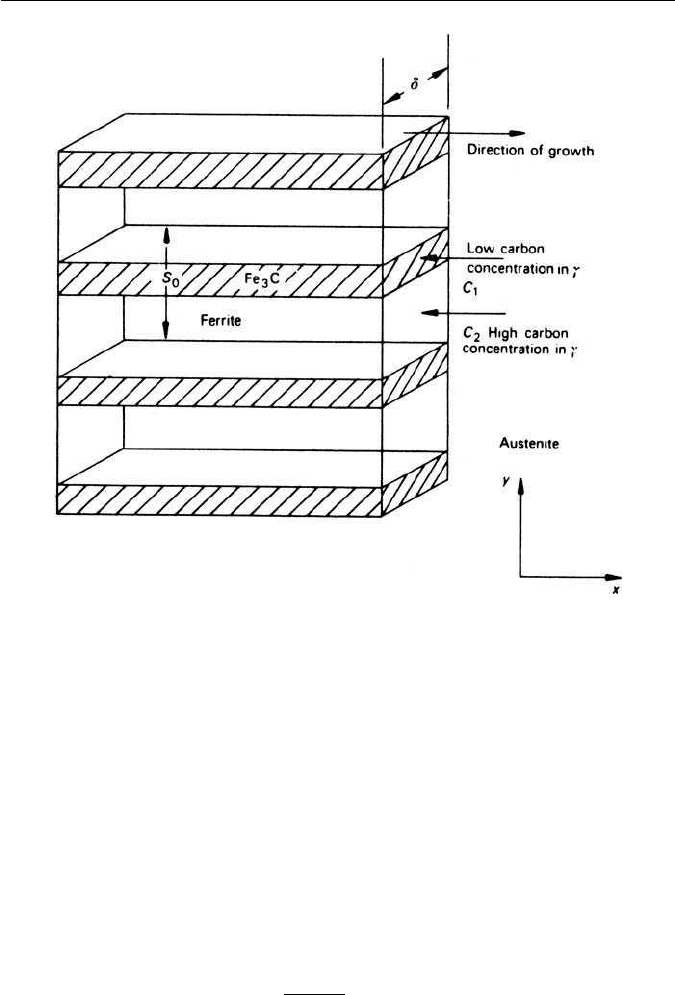
analysis of these observations by considering a volume of pearlite (Fig. 3.17) of

depth δ and interlamellar spacing S

growing unidirectionally in the x-direction.

If growth is allowed to occur by dx then the volume of austenite transformed per

lamellar spacing is S

δ dxρ, where ρ is the density. The free energy G, available

to form this volume of pearlite is:

G = H



− T



δ dxρ, (3.6)

where

= eutectoid temperature

T = transformation temperature

H = latent heat of transformation.

3.5 THE AUSTENITE–PEARLITE REACTION 57

Fig. 3.17 A pearlite growth model.

The formation of this new volume of pearlite causes an increase in interfacial

energy by virtue of the new ferrite and cementite interfaces formed. Therefore:

increase in interfacial area = 2δ dx,

and

increase in interface energy = 2σδ dx, (3.7)

where σ is interfacial energy per unit area.

Growth of the lamellae can only occur if the increases in surface energy is

less than the decrease in energy resulting from the transformation. Therefore,

the condition for growth can be found from Equations (3.4) and (3.5):

H



− T



ρS

= 2σ. (3.8)

This is a very simple treatment which neglects any strain energy term. Also the

free energy change is found from the enthalpy change per unit mass, and it