Bhadeshia H.K.D.H., Honeycombe R. Steels: Microstructure and Properties

Подождите немного. Документ загружается.

PREFACE TO THE SECOND EDITION

This new edition retains the basic framework of the original book; however, the

opportunityhas beentakento introduceseveral additionalchapters dealing with

areas which have emerged or increased in signiﬁcance since the book was ﬁrst

published in 1981. There is now a separate chapter on acicular ferrite which has

become a desirable structure in some steels. The control of microstructures dur-

ing welding is undoubtedly a crucial topic which now requires a chapter, while

the modelling of microstructures to achieve optimum properties has emerged

as an important approach justifying the inclusion of a further new chapter. The

opportunity has also been taken to include a completely revised chapter on

bainite transformations.

The overall aim of the book remains to introduce students to the principles

determining the microstructures of steels, and through these, the mechanical

properties and behaviour in service. Steels remain the most important group

of metallic alloys, possessing a very wide range of microstructures and mechan-

ical properties, which will ensure their continued extensive use far into the

foreseeable future.

RWKH

HKDHB

Cambridge

1995

PREFACE TO THE THIRD EDITION

Steel has the ability to adapt to changing requirements. This comes from the

myriads of ways in which its structure can be inﬂuenced by processing and

alloying. This is why it is the standard against which emerging materials are

compared. Added to this is the commercial success, with output at record levels

and a production efﬁciency which is uncanny. It is pleasing to see how, all over

the world, iron and its alloys contribute to improving the quality of life of so

many human beings. The technology is so good that most of these people rightly

take it for granted.

This new edition captures developments since 1995, e.g., the extremely ﬁne-

grained alloys, steels with the ability to abnormally elongate and the properties

of minute particles of iron. Questions are posed as to the theoretical limit to the

ﬁnest crystals that can be manufactured on a large scale. In addition, there are

major revisions in the explanations of microstructure, strengthening, kinetics

and modelling.

The original aim of this book, to introduce students and technologists to the

principles determining the microstructure and properties of iron and its alloys,

has remained the guiding principle in the new edition.

HKDHB

RWKH

Cambridge

2006

Supporting material accompanying this book

A full set of accompanying exercises and worked solutions for this book are

available for teaching purposes.

Please visit http://www.textbooks.elsevier.com and follow the registration

instructions to access this material, which is intended for use by lecturers

and tutors.

The compilation of questions has been designed to stimulate the student to

explore the subject within the context of the book.

Each question is accompanied by a complete answer, with the exception of

the proposed set of topics for essays. Most of the questions and answers have

been developed as a consequence of many years of teaching and have been

tested on a variety of undergraduates.

IRON AND ITS INTERSTITIAL

SOLID SOLUTIONS

1.1 INTRODUCTION

Steel is frequently the ‘gold-standard’ against which emerging structural mater-

ials are compared. What is often not realized is that this is a moving standard,

with notoriously regular and exciting discoveries being made in the context of

ironand itsalloys.This iswhy steel remainsthemost successfuland cost-effective

of all materials, with more than a billion tonnes being consumed annually in

improving the quality of life. This book attempts to explain why steels continue

to take this pre-eminent position, and examines in detail the phenomena whose

exploitation enables the desired properties to be achieved.

One reason for the overwhelming dominance of steels is the endless variety

ofmicrostructures and propertiesthat canbe generatedby solid-statetransform-

ation and processing. Therefore, in studying steels, it is useful to consider the

behaviour of pure iron ﬁrst, then the iron–carbon alloys, and ﬁnally the many

complexities that arise when further solutes are added.

Pure iron is not an easy material to produce. It has nevertheless been made

with a total impurity content less than 60 parts per million (ppm), of which

10 ppm is accounted for by non-metallic impurities such as carbon, oxygen,

sulphur and phosphorus, with the remainder representing metallic impurities.

Iron of this purity can be extremely weak when reasonably sized samples are

tested: the resolved shear stress of a single crystal at room temperature can be as

low as 10 MN m

−2

, while the yield stress of a polycrystalline sample at the same

temperature can be well below 50 MN m

−2

. However,the shear strength of small

single crystals has been observed to exceed 19,000 MN m

−2

when the size of the

sample is reduced to about 2 µm. This is because the chances of ﬁnding crystal

defects such as dislocations become small as the size of the crystal is reduced.

The theoretical shear strength of a perfect crystal of iron is estimated to be about

21,000 MN m

−2

, equivalent to a tensile strength of about 11,000 MN m

−2

2 CHAPTER 1 IRON AND ITS INTERSTITIAL SOLID SOLUTIONS

For comparison purposes the breaking strength of a very small carbon

nanotube has been measured to be about 130,000 MN m

−2

; this number is so

astonishing that it has led to exaggerated statements about their potential in

structural applications. For example, the tubes are said to be a hundred times

stronger than steel; in fact, there is no carbon tube which can match the strength

of iron beyond a scale of 2 mm, because of the inevitable defects which arise as

the tubes are grown.

The lesson from this is that systems which rely on perfection in order to

achieve strength necessarily fail on scaling to engineering dimensions. Since

perfection is thermodynamically impossible to achieve in large samples, steels

must in practice be made stronger by other means which are insensitive to

size. The mechanisms by which the strength can be increased will be discussed –

sufﬁce it to state here that it is possible to commercially buy steel with a strength

of 5500 MN m

−2

, with sufﬁcient ductility to ensure safe application. Some of

the methods by which such impressive combinations of properties are achieved

without compromising safetywill be discussed,before thewide range ofcomplex

structures which determine the properties is dealt with.

1.2 THE ALLOTROPES OF PURE IRON

At least three allotropes of iron occur naturally in bulk form, body-centred

cubic (bcc, α, ferrite), face-centred cubic (fcc, γ, austenite) and hexagonal close-

packed (hcp, ǫ). The phase β in the alphabetical sequence α, β, γ, δ...is missing

because the magnetic transition in ferrite was at one time incorrectly thought

to be the β allotrope of iron. In fact, there are magnetic transitions in all of the

allotropes of iron. The phase diagram for pure iron is illustrated in Fig. 1.1. Each

point on any boundary between the phase ﬁelds represents an equilibrium state

in which two phases can coexist. The triple point where the three boundaries

intersect represents an equilibrium between all three phases which coexist. It

is seen that in pure iron, the hcp form is stable only at very large pressures,

consistent with its high density. The best comparison of the relative densities of

the phases is made at the triple point where the allotropes are in equilibrium

and where the sum of all the volume changes is zero:

V(bcc → hcp) =−0.34

V(hcp → ccp) =+0.13

V(ccp → bcc) =+0.21







mol

−1

There may exist a fourth natural allotrope in the core of the earth, where the

pressure reaches some three million times that at the surface and where the tem-

perature is estimated to be about 6000

◦

C.The core of the earth is predominantly

iron, and consists of a solid inner core surrounded by a liquid outer core. Know-

ledge of the core is uncertain, but it has been suggested that the crystal structure

of the solid core may be double hcp, although calculations which assume pure

iron,indicate that theǫ-iron remainsthe moststable underinner-core conditions.

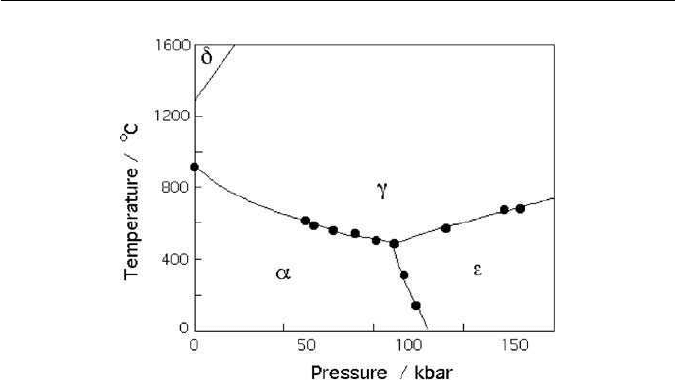
1.2 THE ALLOTROPES OF PURE IRON 3

Fig. 1.1 The phase diagram for pure iron (data from Bundy,1965).The triple point temperature

and pressure are 490

◦

C and 110 kbars, respectively. α, γ and ǫ refer to ferrite, austenite and

ǫ-iron, respectively. δ is simply the higher temperature designation of α.

1.2.1 Thin films and isolated particles

There are two further allotropes which can be created in the form of thin ﬁlms.

Face-centred tetragonal iron has been prepared by coherently depositing iron

as a thin ﬁlm on a {100} plane of a substrate such as copper with which the iron

has a mismatch. The position of atoms in the ﬁrst deposited layer in this case

replicates that of the substrate. A few monolayers can be forced into coherency

in the plane of the substrate with a corresponding distortion normal to the

substrate. This gives the deposit a face-centred tetragonal structure. Growing

iron on a misﬁtting {111} surface of a fcc substrate leads to trigonal iron.

Very thin ﬁlms of iron retain their ferromagnetic character, but there are

special effects due to the small dimensions. The magnetic moment per atom

becomes very large: 3.1 Bohr magnetons compared with 2.2 for bulk α-iron.

This is due to the smaller coordination number for atoms in a thin ﬁlm. The

second effect is that magnetic anisotropy greatly increases for thin ﬁlms because

the spins tend to align normal to the surface. The Curie temperature is greatly

reduced, again because of the change in coordination. For a monolayer of iron

the temperature is just ≃280

◦

Many classical studies of nucleation theory have been conducted on minute

(5–1000 nm) particles of iron where defects responsible for heterogeneous

nucleation can be avoided. Such particles have acquired new signiﬁcance in

that they are exploited in the manufacture of carbon nanotubes. The particles

are deposited due to the decomposition of ferrocene in chemical mixtures which

also contain the ingredients necessary to grow the tubes.

4 CHAPTER 1 IRON AND ITS INTERSTITIAL SOLID SOLUTIONS

Fig. 1.2 A multi-walled carbon nanotube containing a particle of iron (unpublished micrograph

courtesy of I. Kinloch).

It is expected that the coarser particles will have the bcc crystal structure

of ferrite, but it has to be appreciated that a 5 nm particle has about half its

atoms at the surface. Metal surfaces are prone to reconstruction into a variety

of two-dimensional structures which will complicate the interpretation of the

structure of the particle as a whole. The surface also plays another role, in that it

alters the total free energy of the particle leading to a depression of its melting

temperature. It has been estimated that a 5 nm diameter iron particle could

melt at a temperature as low as 500

◦

C. Figure 1.2 illustrates an iron particle

inside a carbon nanotube – its blobby character has been speculated to be due

to melting.

Small metal particles in the size range 1–5 nm are close to a metal/insulator

transition. When observed at the tips of carbon nanotubes using scanning elec-

tron microscopy, the iron particles have shown a tendency to charge, possibly

indicating a loss of metallic behaviour.

1.3 THE PHASE TRANSFORMATION: α- AND γ-IRON

The vast majority of steels rely on just two allotropes, α and γ. Iron is a peculiar

element in that at ambient pressure,bcc ferrite is stable from all temperatures up

to 910

◦

C (the A

point), when it transforms into the fcc austenite, only to revert

to ferrite at 1390

◦

C (theA

point). This high-temperature ferrite is traditionally

labelled δ, although it is no different in crystal structure from α.Theδ-ferrite

remains the stable phase until melting occurs at 1536

◦

Figure 1.3 shows the phase changes in a plot of the mean volume per

atom of iron as a function of temperature. It should be noted that the γ-to

α-transformation is accompanied by an atomic volume change of approximately

1%, which can lead to the generation of internal stresses during transformation.

The detailed geometry of unit cells of α- and γ-iron crystals is particularly

relevant to, e.g., the solubility in the two phases of non-metallic elements such

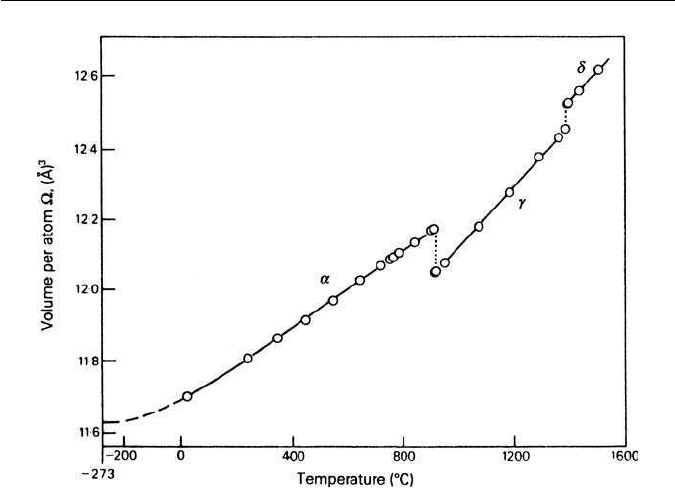
1.3 THE PHASE TRANSFORMATION: α- AND γ-IRON 5

Fig. 1.3 Temperature dependence of the mean volume per atom in iron crystals

(Hume-Rothery,The Structure of Alloys of Iron, Pergamon Press, Oxford, UK, 1966).

as carbon and nitrogen, the diffusivity of alloying elements at elevated tem-

peratures and the general behaviour on plastic deformation. The bcc structure

of α-iron is more loosely packed than that of fcc γ-iron (Figs 1.4a, b). The

largest cavities in the bcc structure are the tetrahedral holes existing between

two edge and two central atoms in the structure, which together form a tetra-

hedron (Fig. 1.4c). The second largest are the octahedral holes which occupy

the centres of the faces and the 001 edges of the body-centred cube (Fig.

1.4d). The surrounding iron atoms are at the corners of a ﬂattened octahedron

(Fig. 1.4e). It is interesting that the fcc structure, although more closely packed,

has larger holes than the bcc structure. These holes are at the centres of the

cube edges, and are surrounded by six atoms in the form of an octagon, so they

are referred to as octahedral holes (Fig. 1.4f). There are also smaller tetrahe-

dral interstices. The largest sizes of spheres which will enter these interstices are

given in Table 1.1.

The α ⇋ γ transformation in pure iron occurs very rapidly, so it is not gen-

erally possible to retain the high-temperature fcc form at room temperature.

Rapid quenching can substantially alter the morphology of the resulting α-iron,

but it still retains its bcc structure. It follows that any detailed study of austenite

in pure iron must be done at elevated temperatures, e.g. using X-ray or neutron

diffraction. The transformation of the austenite on cooling can also be followed

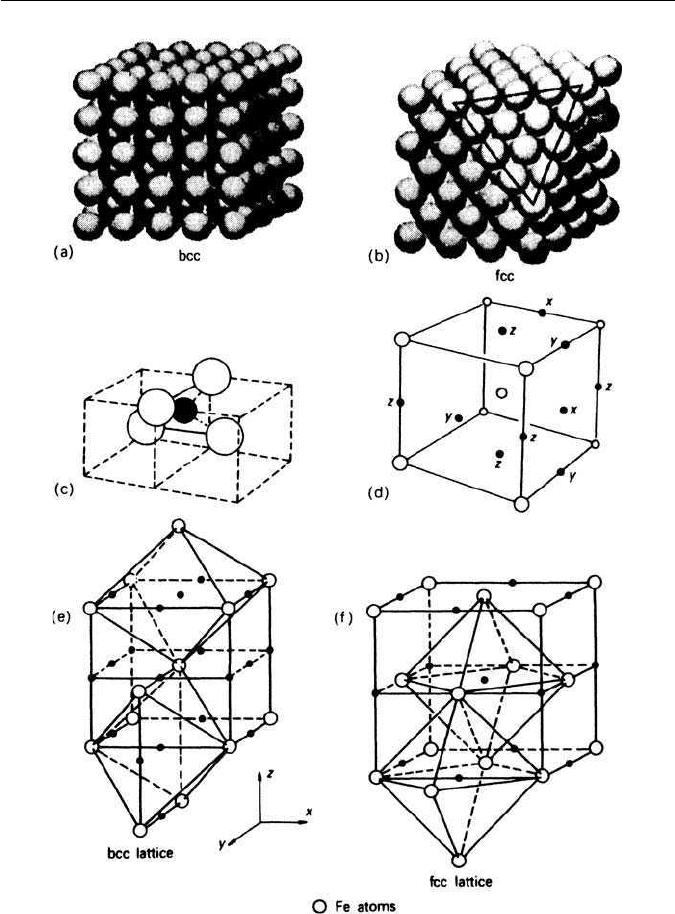
6 CHAPTER 1 IRON AND ITS INTERSTITIAL SOLID SOLUTIONS

Fig. 1.4 (a) bcc structure, (b) fcc structure (Moffat, Pearsall and Wulff,The Structure and Prop-

erties of Materials: Vol. 1, Structure, John Wiley, USA, 1964), (c) tetrahedral interstices in bcc

structure, (d) octahedral interstices in bcc structure (Hume-Rothery,The Structure of Alloys of

Iron, Pergamon Press, Oxford, UK, 1966), (e) and (f) octahedral interstices in bcc and fcc iron

(Cohen,Transactions of the Metallurgical Society of AIME 224, 638, 1962).

1.3 THE PHASE TRANSFORMATION: α- AND γ-IRON 7

Table 1.1 Size of largest spheres fitting interstices in bcc and

fcc iron

Radius Radius in iron (Å)

bcc Tetrahedral 0.29r 0.37

Octahedral 0.15r 0.19

fcc Tetrahedral 0.23r 0.28

Octahedral 0.41r 0.51

r =atomic radius of iron.

using diffraction based on the intense X-rays generated in a synchrotron, or

using precision dilatometry. The latter technique relies on the volume change

accompanying the transformation from austenite to ferrite.

There are circumstances where it is necessary to study pure austenite at

temperatures well below ambient. Pure iron can be retained in its austenitic

state to very low temperatures by coherent precipitation in copper. Copper has

an fcc crystal structure and hence prevents the coherent particles of austenitic

iron from transforming during cooling.This technique has been used to establish

the antiferromagnetic nature of the austenite with a Néel temperature of about

−190

◦

C (the austenite is ferromagnetic at high temperatures, with a Curie point

of some 1525

◦

C).

1.3.1 Mechanisms of transformation

One of the reasons why there is a great variety of microstructures in steels is

because the same allotropic transition can occur with a variety of ways in which

the atoms can move to achieve the change in crystal structure. The transform-

ation can occur either by breaking all the bonds and rearranging the atoms into

an alternative pattern (reconstructive transformation), or by homogeneously

deforming the original pattern into a new crystal structure (displacive or shear

transformation) (Fig. 1.5).

In the displacive mechanism the change in crystal structure also alters the

macroscopic shape of the sample when the latter is not constrained. The shape

deformation during constrained transformation is accommodated by a com-

bination of elastic and plastic strains in the surrounding matrix. The product

phase grows in the form of thin plates to minimize the strains. The atoms are

displaced into their new positions in a coordinated motion. Displacive transfor-

mations can, therefore, occur at temperatures where diffusion is inconceivable

within the time scale of the experiment. Some solutes may be forced into the

product phase, a phenomenon known as solute trapping. Both the trapping of

atoms and the strains make displacive transformations less favourable from a

thermodynamic point of view.

It is the diffusion of atoms that leads to the new crystal structure during

a reconstructive transformation. The ﬂow of matter is sufﬁcient to avoid any