Bhadeshia H.K.D.H., Honeycombe R. Steels: Microstructure and Properties

Подождите немного. Документ загружается.

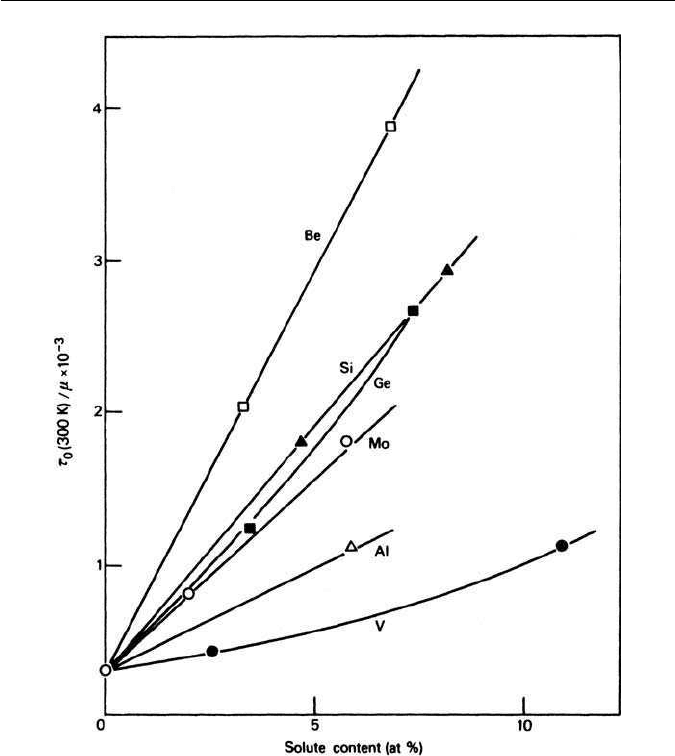
28 CHAPTER 2 THE STRENGTHENING OF IRON AND ITS ALLOYS

Fig. 2.7 Solid solution strengthening of α-iron crystals by substitutional solutes. Ratio of the

critical resolved shear stress τ

to shear modulus µ as a function of atomic concentration

(Takeuchi, Journal of the Physical Society of Japan 27, 929, 1969).

iron by Hall and Petch, led to the Hall–Petch relationship between the yield

stress σ

and the grain diameter d,

= σ

+ k

−½

, (2.9)

where σ

and k

are constants. This type of relationship holds for a wide variety

of irons and steels as well as for many non-ferrous metals and alloys. A typical

set of results for mild steel is given in Fig. 2.7, where the linear relationship

between σ

and d

−½

is clearly shown for the three test temperatures.

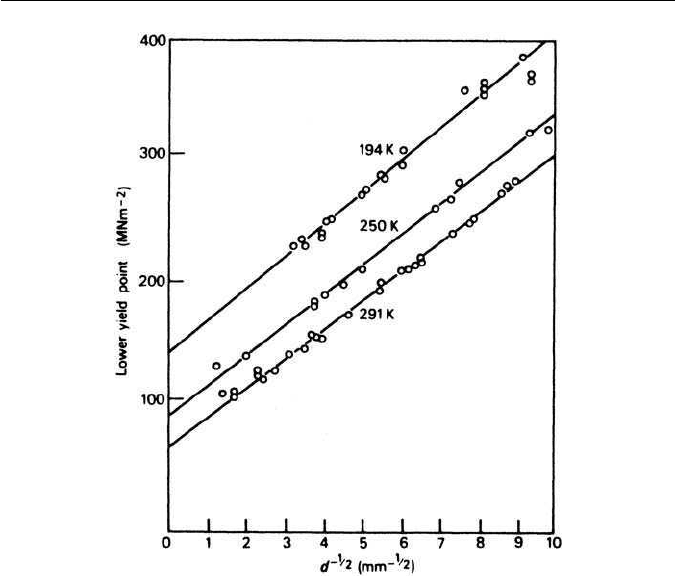
2.5 GRAIN SIZE 29

Fig. 2.8 Dependence of the lower yield stress of mild steel on grain size (Petch, in Fracture

(eds Averbach et al.), John Wiley, USA, 1959).

The constant σ

is called the friction stress. It is the intercept on the stress axis,

representing the stress required to move free dislocations along the slip planes

in the bcc crystals, and can be regarded as the yield stress of a single crystal

−½

=0). This stress is particularly sensitive to temperature (Fig. 2.7) and com-

position. The k

term represents the slope of the σ

−d

−½

plot which has been

found not to be sensitive to temperature (Fig. 2.8), composition and strain rate.

In line with the Cottrell–Bilby theory of the yield point involving the break

away of dislocations from interstitial carbon atmospheres, k

has been referred

to as the unpinning parameter. However, the insensitivity of k

to temperature

suggests that unpinning rarely occurs, and emphasizes the theory that new dis-

locations are generated at the yield point. This is consistent with the theories

explaining the yield point in terms of the movement of new dislocations, the

velocities of which are stress dependent (Section 2.3.2).

The grain size effect on the yield stress can therefore be explained by assum-

ing that a dislocation source operates within a crystal causing dislocations to

move and eventually to pile-up at the grain boundary. The pile-up causes a

stress to be generated in the adjacent grain, which, when it reaches a critical

30 CHAPTER 2 THE STRENGTHENING OF IRON AND ITS ALLOYS

value, operates a new source in that grain. In this way, the yielding process is

propagated from grain to grain. This can be observed macroscopically by the

passage of a Luders band. The grain size determines the distance dislocations

have to move to form grain boundary pile-ups, and thus the number of disloca-

tions involved. With large grain sizes, the pile-ups will contain larger numbers

of dislocations which will in turn cause higher stress concentrations in neigh-

bouring grains. The shear stress τ

at the head of a dislocation pile-up is equal

to nτ, where n is the number of dislocations involved and τ is the shear stress

on the slip plane. This means that the coarser the grain size, the easier it will be

to propagate the yielding process.

In practical terms, the ﬁner the grain size, the higher the resulting yield stress

and, as a result, in modern steel working much attention is paid to the ﬁnal fer-

rite grain size. While a coarse grain size of d

−½

=2, i.e. d =0.25 mm, gives a

yield stress in mild steels of around 100 MN m

−2

, grain reﬁnement to d

−½

=20,

i.e. d =0.0025 mm, raises the yield stress to over 500 MN m

−2

, so that achieving

grain sizes in the range 2–10 µm is extremely worthwhile. Over the last 40 years,

developments in rolling practice and the addition of small concentrations of

particular alloying elements to mild steels, have resulted in dramatic improve-

ments in the mechanical properties of this widely used engineering material

(Chapter 9).

2.5.2 Nanostructured steels

Modern technologies allow steels to be made routinely and in large quantities

with grain sizes of about 1 µm. Limited processes, generally involving severe

thermomechanical processing, have been developed to achieve nanostructured

ferrite grains in steel, with a size in the range 20–100 nm. Experiments have

revealed that the Hall–Petch equation holds down to some 20 nm, conﬁrming

that enormous strengths can be achieved by reﬁning the grain size. The equation

begins to fail at grain sizes less than about 20 nm, possibly because other mecha-

nisms of deformation, such as grain boundary sliding, begin to play a prominent

role. The volume fraction V

of material occupied by the boundaries is given

by:

≃ 2a/

where

L is the mean linear intercept deﬁning the grain size and a is the thickness

of the boundary layer. Clearly, the fraction of atoms located at the grain sur-

faces becomes very large in the nanostructured materials, facilitating diffusional

processes such as grain sliding (Fig. 2.9).

Although the nanostructured steels are strengthened as expected from the

Hall–Petch equation, they tend to exhibit unstable plasticity after yielding. The

plastic instability occurs in both tension and in compression testing, with shear

bands causing failure in the latter case. It is as if the capacity of the material to

work harden following yielding diminishes. The consequence is an unacceptable

2.5 GRAIN SIZE 31

(a)

(b)

Fig. 2.9 (a) The volume fraction of grain boundary within a given volume, as a function of the

grain size. (b) Loss of ductility as the strength is increased by dramatically reducing the grain

size in aluminium and iron alloys (Tsuji, Ito, Saito and Minamino, Scripta Materialia 47, 893, 2002,

reproduced with permission from Elsevier).

reduction in ductility as the grain size is reduced in the nanometre range. At

very ﬁne grain sizes, the conventional mechanisms of dislocation multiplication

fail because of the proximity of the closely space boundaries. It then becomes

impossible to accumulate dislocations during deformation. Grain boundaries

are also good sinks for defects. This would explain the observed inability of

nanostructured materials to work harden. One way of overcoming this difﬁculty

is described in Chapter 6.

The difﬁculty that nanocrystalline grains have in deforming by a dislocation

mechanism is highlighted in recent experiments

where nanocrystals of ferrite

Ivanisenk, Y., MacLaren, I., Vailiev, R. Z., and Fecht, H.–J., Advanced Engineering

Materials 7, 1011, 2005.

32 CHAPTER 2 THE STRENGTHENING OF IRON AND ITS ALLOYS

were forced to deform in shear. The crystals underwent a shear transformation

into austenite.

2.6 DISPERSION STRENGTHENING

In all steels there is normally more than one phase present, and indeed it is often

the case that several phases can be recognized in the microstructure. The matrix,

which is usually ferrite (bcc structure) or austenite (fcc structure) strengthened

by grain size reﬁnement and by solid solution additions, is further strengthened,

often to a considerable degree,by controlling the dispersions of the other phases

in the microstructure. The commonest other phases are carbides formed as a

result of the low solubility of carbon in α-iron. In plain carbon steels this carbide

is normally Fe

C (cementite) which can occur in a wide range of structures from

coarse lamellar form (pearlite), to ﬁne rod or spheroidal precipitates (tempered

steels). In alloy steels, the same range of structures is encountered, except that

in many cases iron carbide is replaced by other carbides which are thermo-

dynamically more stable. Other dispersed phases which are encounteredinclude

nitrides, intermetallic compounds and, in cast irons, graphite.

Most dispersions lead to strengthening, but often they can have adverse

effects on ductility and toughness. In ﬁne dispersions, ideally small spheres

randomly dispersed in a matrix, there are well-deﬁned relationships between

the yield stress, or initial ﬂow stress, and the parameters of the dispersion. The

simplest is that due to Orowan relating the yield stress of the dispersed alloy

to the interparticle spacing :

= τ

b/2

, (2.10)

where τ

is the yield strength of the matrix, T is the line tension of a dislocation

and b is the Burgers vector. This result emerges from an analysis of the move-

ment of dislocations around spherical particles, showing that the yield stress

varies inversely as the spacing between the particles. If the dispersion is coars-

ened by further heat treatment, the strength of the alloy falls. A more precise

form of the Orowan equation, due to Ashby, takes into account the radius r of

the particles:

= τ

φ ln



 − 2r



( − 2r)/2



, (2.11)

where φ is a constant and G is the shear modulus.

These relationships can be applied to simple dispersions sometimes found

in steels, particularly after tempering, when, in plain carbon steels, the structure

consists of spheroidal cementite particles in a ferritic matrix. However, they can

provide approximations in less ideal cases, which are the rule in steels, where the

dispersions vary over the range from ﬁne rods and plates to irregular polyhedra.

2.7 AN OVERALLVIEW 33

Fig. 2.10 Dependence of the flow stress at several strains on the MFFP in a pearlitic steel

(Takahashi and Nagumo,Transactions of the Japan Institute of Metals 11, 113, 1970).

Perhaps the most familiar structure in steels is that of the eutectoid pearlite,

usually approximated as a lamellar mixture of ferrite and cementite. This can

be considered as an extreme form of dispersion of one phase in another, and

undoubtedly provides a useful contribution to strengthening. The lamellar spa-

cing can be varied over wide limits, and again the strength is sensitive to such

changes (see Chapter 3). When the coarseness of the pearlite is represented by a

mean uninterrupted free ferrite path (MFFP) in the pearlitic ferrite, it has been

shown that the ﬂow stress is related to MFFP

−½

, i.e. there is a relationship of

the Hall–Petch type (Fig. 2.10).

2.7 AN OVERALL VIEW

Strength in steels arises from several phenomena, which usually contribute col-

lectively to the observed mechanical properties. The heat treatment of steels is

aimed at adjusting these contributions so that the required balance of mechan-

ical properties is achieved. Fortunately the γ/α change allows a great variation

in microstructure to be produced, so that a wide range of mechanical proper-

ties can be obtained even in plain carbon steels. The additional use of metallic

alloying elements, primarily as a result of their inﬂuence on the transformation,

34 CHAPTER 2 THE STRENGTHENING OF IRON AND ITS ALLOYS

provides an even greater control over microstructure, with consequent beneﬁts

in the mechanical properties.

We have not discussed in this chapter the strengthening and deformation

behaviour of mixed microstructures, such as the dual-phase steels which consist

of ferrite and harder martensite. This can radically alter the stress versus strain

behaviour with the deformation being heterogeneous on a microscopic scale

with complex constraint and compatibility issues governing plasticity. Some of

these aspects of mixed microstructures are described in Chapter 14 as one of

the two case studies.

2.8 SOME PRACTICAL ASPECTS

The presence of a sharp yield point in a steel can be detrimental to its behaviour,

e.g., when used for pressings, where complex patterns of Luders bands can pro-

duce rough surfaces and lead to poor workability. The severity of the yield point

is directly related to the amount of carbon and nitrogen in solution in the ferrite,

so that steps taken to reduce these concentrations are helpful. Unfortunately,

yield points can be obtained with very low concentrations of carbon and nitro-

gen, and it is impracticable in industrial conditions to obtain steels below these

limits. However, any heat treatment which reduces interstitial solid solution is

beneﬁcial, e.g. slow cooling from annealing treatments. The yield point can be

more reliably eliminated prior to working by a small amount of cold rolling

(0.5–2%), referred to as temper rolling. As both nitrogen and carbon diffuse

appreciably in ferrite at ambient temperatures, it is desirable to fabricate steels

soon after rolling and annealing.

While carbon and nitrogen can both cause strain ageing and consequently a

yield point, the higher solubility of nitrogen in ferrite means that it provides the

greater problem in steels used for deep drawing and pressing. Steps are taken

during steelmaking to keep the nitrogen level down, but to minimize its effects,

the easiest solution is to add small concentrations of strong nitride formers such

as aluminium, titanium or vanadium, which reduce the nitrogen in solution to

very low levels.

The occurrence of strain ageing can, by increasing both the yield stress and

ultimate tensile stress, beneﬁt mild steels which are used for constructional

purposes. Furthermore, the fatigue properties are improved, both at room tem-

perature and in the range up to 350

◦

C. The existence of a well-deﬁned fatigue

limit in steels, i.e. a fatigue stress limit below which failure does not occur, has

been linked to the occurrence of strain ageing during the test, but even very pure

iron shows the same behaviour. It should be emphasized that even in a relatively

simple low carbon steel, the strength arises not only from these effects of car-

bon and nitrogen, but also from the solid solution hardening of elements such as

silicon and manganese, and potentially from the reﬁnement of the ferrite grain

size by various means.

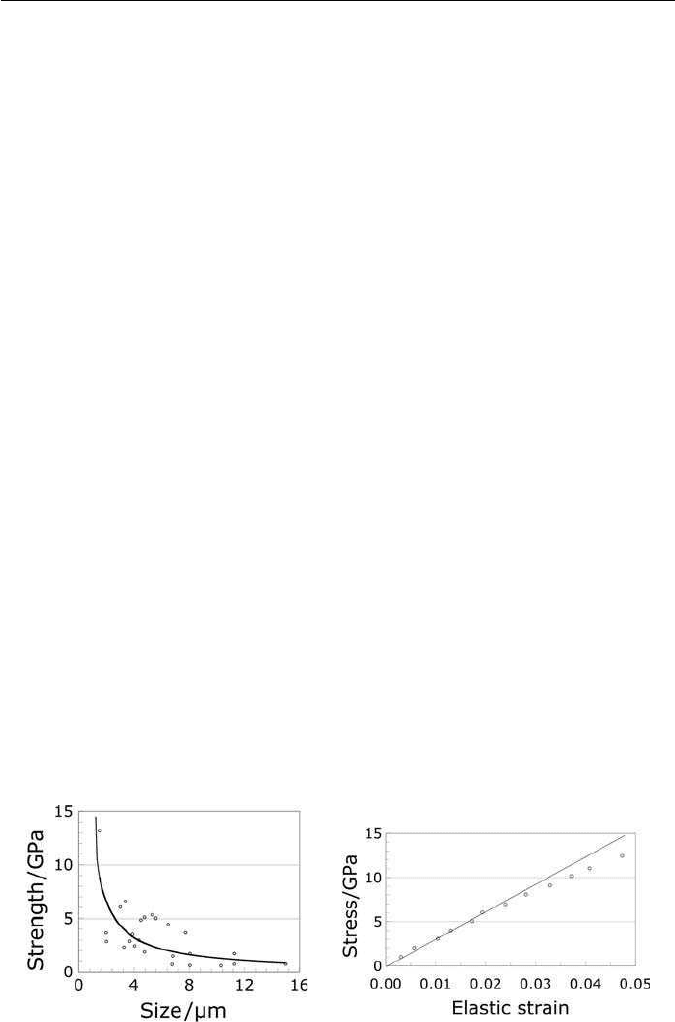
2.9 LIMITS TO STRENGTH 35

2.9 LIMITS TO STRENGTH

Strength is not always a useful entity. It may not in fact be safe to load an

engineering structure to the full capability of the material. To illustrate this

and some other limits of scale, a comparison is presented here of the potential

strength of steel and that of carbon nanotubes which are the subject of much

contemporary discussion.

2.9.1 Theoretical strength

The strength of crystals increases sharply as they are made smaller. This is

because the chances of avoiding defects become greater as the volume of the

sample decreases. In the case of metals, imperfections in the form of disloca-

tions are able to facilitate shear at much lower stresses than would be the case if

whole planes of atoms had to collectively slide across each other. Since defects

are very difﬁcult or impossible to avoid, the strength in the absence of defects

is said to be that of an ideal crystal.

In an ideal crystal, the tensile strength σ

≃0.1E where E is the Young’s

modulus. The corresponding ideal shear strength is σ

≃bµ/2πa, where µ is the

shear modulus, b is a repeat period along the displacement direction and a is the

spacing of the slip planes. For ferritic iron, µ =80.65 GPa and E ≃208.2 GPa.

It follows that the ideal values of tensile and shear strength should be about

21 and 11 GPa,respectively. In fact,tensile strengths approaching the theoretical

values were achieved by Brenner as long ago as 1956 (Fig. 2.11a) during the

testing of whiskers of iron with diameters less than 2 µm. It is interesting that

these stress levels fall out of the regime where Hooke’s law applies (Fig. 2.11b).

The strength decreased sharply as the dimensions of the whiskers were

increased (Fig. 2.11a), because the chances of ﬁnding defects increase as the

sample gets bigger. It was therefore recognized many decades ago that it

is not wise to rely on perfection as a method of designing strong materials,

(a) (b)

Fig. 2.11 (a)The tensile strength of whiskers of iron. (b) Non-linear elasticity at large stresses

(after Brenner, S.,Acta Metallurgica 4, 62, 1956; Journal of Applied Physics 27, 1484, 1956).

36 CHAPTER 2 THE STRENGTHENING OF IRON AND ITS ALLOYS

although itremains the case that incredible strength can be achieved by reducing

dimensions, in the case of iron, to a micrometre scale.

It is in this context that we now proceed to examine the notion that large-

scale engineering structures can be designed using very long carbon nanotubes.

The particular structure proposed is a space elevator to replace rocket launches,

and would require ropes which are some 120,000 km in length.

2.9.2 Gigatubes

Carbon nanotubes can be imagined to be constructed from sheets of graphene

consisting of sp

carbon arranged in a two-dimensional hexagonal lattice

(Fig. 2.12). The sheets, when rolled up and with the butting edges appropri-

ately bonded, are the nanotubes, which may or may not be capped by fullerne

hemispheres. The actual form can be complex, e.g. with occasional pentagonal

rings of carbon atoms instead of hexagonal to accommodate changes in shape.

The breaking strength of such a tube has been estimated to be an extra-

ordinary 130 GPa; this number is astonishing and has led to many exaggerated

comparisons againststeel. However,this is thestrength of aninvisibly small nan-

otube. Larger tubes will contain defects which lead to a gross deterioration of

strength,rather like the behaviour of whiskers of iron. Some of these defects will

be there at equilibrium and hence are unavoidable. For example, it is known that

metals contain an equilibrium concentration of vacancies. The enthalpy change

associated with the formation of a vacancy opposes its existence, whereas the

change in conﬁgurational entropy due to the formation of a vacancy favours its

Fig. 2.12 Schematic diagram showing how a sheet of graphene might be rolled to form a tube

(courtesy of M. Endo).

Edwards, B. C.,Acta Astronautica 47, 735, 2000.

2.9 LIMITS TO STRENGTH 37

formation. The total change in free energy on forming n vacancies in a crystal

is given by:

G = ng − kT[(N + n)ln{N + n}−N ln{N}−n ln{n}],

where k is the Boltzmann constant, T is the absolute temperature, N is the num-

ber of atoms, g =h −Ts, h is the enthalpy of formation of one vacancy

and s is the entropy of formation of a vacancy excluding any contribution from

conﬁgurational entropy, which is the second term in the equation. The equilib-

rium mole fraction of vacancies (x) is obtained by writing ∂G/∂n =0 giving:

x = n/N ≃ exp{−g/kT}.

On this basis, and taking the energy of a vacancy in a nanotube as 7 eV, and

setting T to be the manufacturing temperature of the tubes (2000–4000 K), it is

possible to show that a carbon nanotube strand appropriate for a space elevator,

weighing 5000 kg, would roughly 10

–10

defects. It is not therefore possible to

scale the properties of a nanotube by some 18 orders of magnitude and assume

that the strength will be retained.

This emphasizes again that systems which rely on perfection in order to

achieve strength necessarily fail on scaling to engineering dimensions. Indeed,

there is no carbon tube which can match the strength of iron beyond a scale

of 2 mm.

2.9.3 Fracture

Suppose that gigatubes of carbon could be made capable of supporting a stress

of 130 GPa. Would this allow for safe engineering design? One aspect of safe

design is that fast fracture should be avoided; most metals absorb energy in the

form of plastic deformation before ultimate fracture. Energy absorption in an

accident is a key aspect of automobile safety. Carbon nanotubes are not in this

sense defect tolerant; their deformation prior to fracture is elastic. The stored

energy density in a tube stressed to 130 GPa, given an elastic modulus along its

length of E =1.2TPa is in excess of that associated with dynamite (Table 2.1).

Dynamite is explosive because of its high energy density and because this energy

is released rapidly, the detonation front propagating at some 6000 m s

−1

.The

speed of an elastic wave in the carbon is given by



E/ρ where ρ is the density.

In the event of fracture,the rate at which the stored energy would be released is

much greater than that of dynamite (Table 2.1),meaning that fracture is unlikely

to occur in a safe manner.

It follows that structures in tension, which reversibly store energy far in

excess of their ability to do work during fracture must be regarded as unsafe.

Christian, J.W.,Theory of Transformations in Metals and Alloys, 3rd edition, Pergamon Press,

Oxford, 2003.