Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


10 Fluctuation Phenomena in Superconductors 399
˛ˇ
(D)
=
4
e
2
˛T
p
v
˛
p
v
ˇ
p
"
3
p
(10.118)
= ı
˛ˇ
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
e
2
32
1
√
3D case,
e
2
16d
1
2D film, thickness: d ,
e
2
16S
1
3/2
1D wire, cross-section: S
2
.
One can compare this result with that carried out
in the Introduction from qualitative considerations,
based on the Drude formula. Those simple specula-
tionscorrectly reflectthephysicsofthe phenomenon
but were carried out with the assumption of the
momentum independence of the relaxation time
p
,
taken as
0
=
8(T−T
c
)
. As we have just seen, in reality
p
decreases rapidly with increase of the momentum,
the excess “2” appeared in (10.115) because of the
wave nature of fluctuation Cooper pairs; accounting
for this circumstance results in the precise coeffi-
cients of (10.119), which is different from (10.11).
An especially simple form of the paraconductiv-
ity results in the 2D case, where, calculated per unit
square, it depends on the reduced temperature only:
(T)=
e
2
16
T
T − T
c
. (10.119)
The coefficient in this formula turns out to be a uni-
versal constant and is given by the value /e
2
=
4.1k§.For electronic spectra of other dimensionali-
ties this universality is lost, and the paraconductivity
comes to depend on the electron mean free path.
Let us compare
(T) with the normal electron
Drude part
n
= n
e
e
2
/m by writing the total con-
ductivity
=
e
2
p
F
l
2
+
1
16
. (10.120)
One sees that at
cr
=0.4/(p
F
l) ∼ Gi
(2c)
the fluc-
tuation correction reaches the value of the normal
conductivity.Let us recall that thesameorderof mag-
nitude for the 2D Ginzburg–Levanyuk number was
obtained above from the heat capacity study.We will
discuss the region of applicability of (10.120) below
in Sect. 10.8.
Itis worthmentioning that the results derivedhere
for paraconductivity are valid with the assumption
of weak fluctuations: for the temperature range
Gi
(D)
they are no longer applicable. Nevertheless, one
can see that for not very dirty films, with p
2
F
ld 1,
a wide region of temperatures Gi
(2d)
1exists
where the temperature dependence of conductivity
is determined by fluctuations and in this region the
localization effects are negligible.
The transport equation (10.115) was originally
derived many years ago by L.G. Aslamazov and
A.I. Larkin [71]. Recently T. Mishonov et al. [72] red-
erived (10.115) and solved it for n
p
inthecaseofan
arbitrary electric field.
10.4.3 General Expression f or Paraconductivity
Unfortunately the applicability of the master equa-
tion derived is restricted to weak magnetic fields
(H H
c2
()). For stronger fields H
c2
() H
H
c2
(0) the simple evaluation of averages in (10.114)
turns out to be incorrect; thedensity matrix has to be
introduced and the master equation loses its attrac-
tive simplicity.At the same time,as we already know,
precisely these fields, which quantize the fluctuation
Cooper pair motion, deserve special interest. This is
why in order to include in the scheme the magnetic
field and frequency dependencies of theparaconduc-
tivity, we return to the analysis of the general TDGL
equation (10.104) without the objective to reduce it
to a Boltzmann type transport equation.
Let us solve it in the case when the applied elec-
tric field can be considered as a perturbation. The
method will much resemble an exercise from a
course of quantum mechanics. To carry out the nec-
essary generality side byside with a formal simplicity
of expressions we will introduce some kind of sub-
script {i}which includes the complete set of quantum
numbers and time.By a repeated subscript a summa-
tion over a discrete and integration over continuous
variables (time in particular) will be supposed.
We will look for the response of the order param-
eter to a weak electric field applied in the form
¦
k
z
(r,t)=¦
(0)
{i}
+ ¦
(1)
{i}
, (10.121)
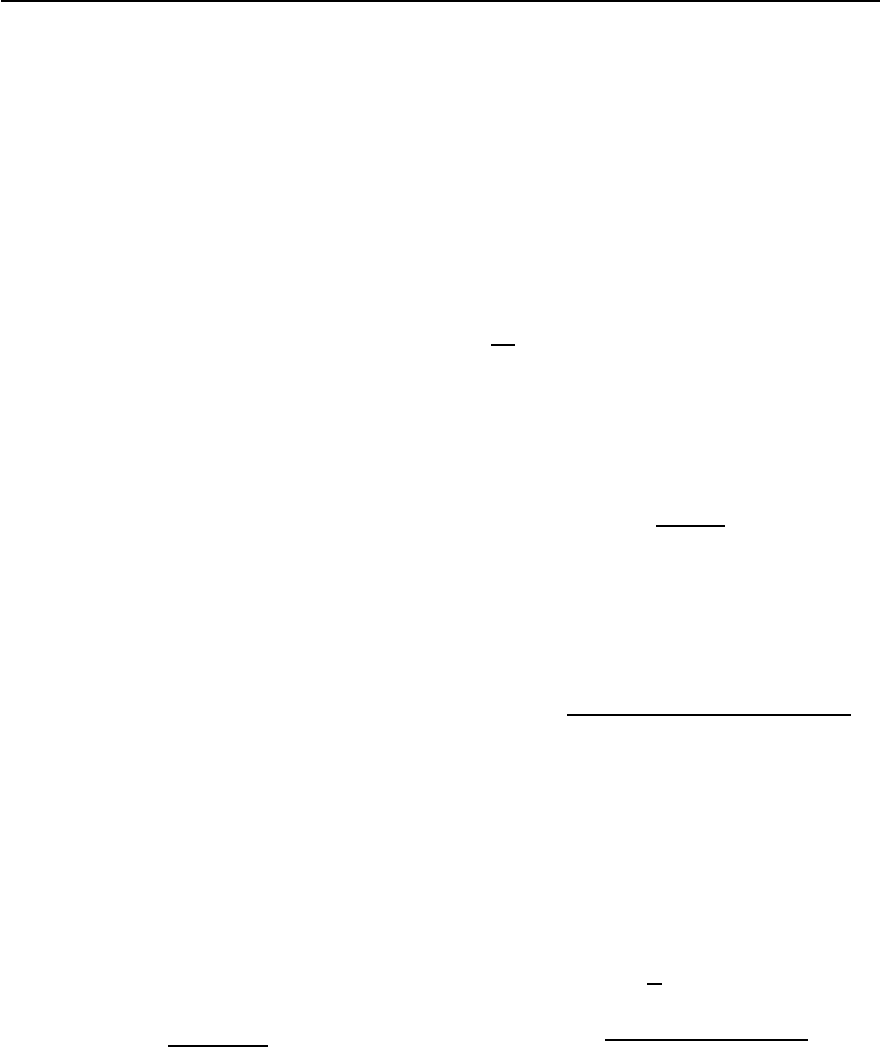
400 A.I. Larkin and A.A.Varlamov
where ¦
(0)
{i}
is determined by (10.107). Substituting
this expression into (10.105) and restrictingour con-
sideration to linear terms in the electric field we can
write
(
B
L
−1
)
{ik}
¦
(1)
{k}
=2ie
GL
'
{il}
¦
(0)
{l}
,
with the solution in the form
¦
(1)
{i}
=2ie
GL
B
L
{ik}
'
{kl}
B
L
{lm}
{m}
.
Let us substitute the order parameter (10.121) in the
quantum mechanical expression for current
j =2e Re
¦
(0)∗
{i}
Bv
{ik}
¦
(1)
{k}
+ ¦
(1)∗
{i}
Bv
{ik}
¦
(0)
{k}
, (10.122)
whereBv
{ik}
is the velocity operator, which can be ex-
pressedby means of the commutator of r withHamil-
tonian (10.107):
Bv
{ik}
= i{
B
H, r}
{ik}
. (10.123)
The second term of (10.122) can be written by means
of a transposed velocity operator (which is Hermi-
tian) as the complex conjugated value of the first one:
¦
(1)∗
{i}
Bv
{ik}
¦
(0)
{k}
=(¦
(0)∗
{k}
Bv
{ik}
¦
(1)
{i}
)
∗
, (10.124)
which results in
j =2Re{¦
(0)∗
{i}
(2eBv
{ik}
)¦
(1)
{k}
} (10.125)
=−8e
2
Im{
GL
B
L
∗
{ki}
Bv
{il}
B
L
{lm}
'
{mn}
B
L
{np}
∗
{k}
{p}
}.
Let us average now (10.126) over the Langevin forces
moving the operator
B
L
∗
{ki}
from the beginning to the
end of the trace and using (10.108). One finds
j =−16Te
2
Re(
GL
) (10.126)
×Im{
GL
Bv
{il}
B
L
{lm}
'
{mn}
B
L
{np}
B
L
∗
{pi}
}.
Now we choose the representation where the
B
L
{lm}
op-
erator is diagonal (it is evidently given by the eigen-
functions of the Hamiltonian (10.107)):
L
{m}
(§)=
1
"
{m}
− i§
GL
, (10.127)
where "
{m}
are the appropriate energy eigenvalues.
Then we assume that the electric field is coordinate
independent but is a monochromatic periodic func-
tion of time:
'(r,t)=−E
ˇ
r
ˇ
exp(−i!t) . (10.128)
In doing the Fourier transform in (10.127) one has
to remember that the time dependence of the matrix
elements '
{mn}
results in a shift of the frequency vari-
able of integration § → § − ! in both L-operators
placed after '
{mn}
or, what is the same, to a shift of
the argument of the previous
B
L
{lm}
for !:
j
˛
!
=16Te
2
Re(
GL
) (10.129)
×
d§
2
%
GL
Bv
˛
{il}
B
L
{l}
(§ + !)[−ir
ˇ
{li}
]
B
L
{i}
(§)
B
L
∗
{i}
(§)
E
ˇ
,
where %f (!) ≡ [f (!)+f
∗
(−!)]/2.
Let us express the matrix element r
{li}
by means
ofBv
{li}
usingthe commutation relation (10.123).One
can see that in the representation chosen
Br
ˇ
{li}
= i
Bv
ˇ
{li}
"
{i}
− "
{l}
, (10.130)
and, carrying out the frequency integration in
(10.129),one finally gets for the fluctuation conduc-
tivity tensor (j
˛
!
=
˛ˇ
(!)E
ˇ
):
˛ˇ
(, H, !)=8e
2
T Re(
GL
) (10.131)
×
∞
{i,l}=0
%
$
GL
Bv
˛
{il}
Bv
ˇ
{li}
"
{i}
(
GL
"
{i}
+
∗
GL
"
{l}
− i|
GL
|
2
!)("
{l}
− "
{i}
)
&
.
This is the most general expression describing the
d.c., galvanomagnetic and high frequency paracon-
ductivitycontribution.When we are interested in di-
agonal effects only, where it is enough to accept
GL
as real (
GL
=Re
GL
= ˛/8) omitting its small
imaginary part, the last expression can be simplified
by means of symmetrization of the summation vari-
ables:
˛˛
(, H, !)=
2
˛e
2
T (10.132)
×
∞
{i,l}=0
%
Bv
˛
{il}
Bv
˛
{li}
"
{i}
"
{l}
("
{i}
+ "
{l}
− i
GL
!)
,
Let us demonstrate the calculation of the d.c.para-
conductivity in the simplest case of a metal with an
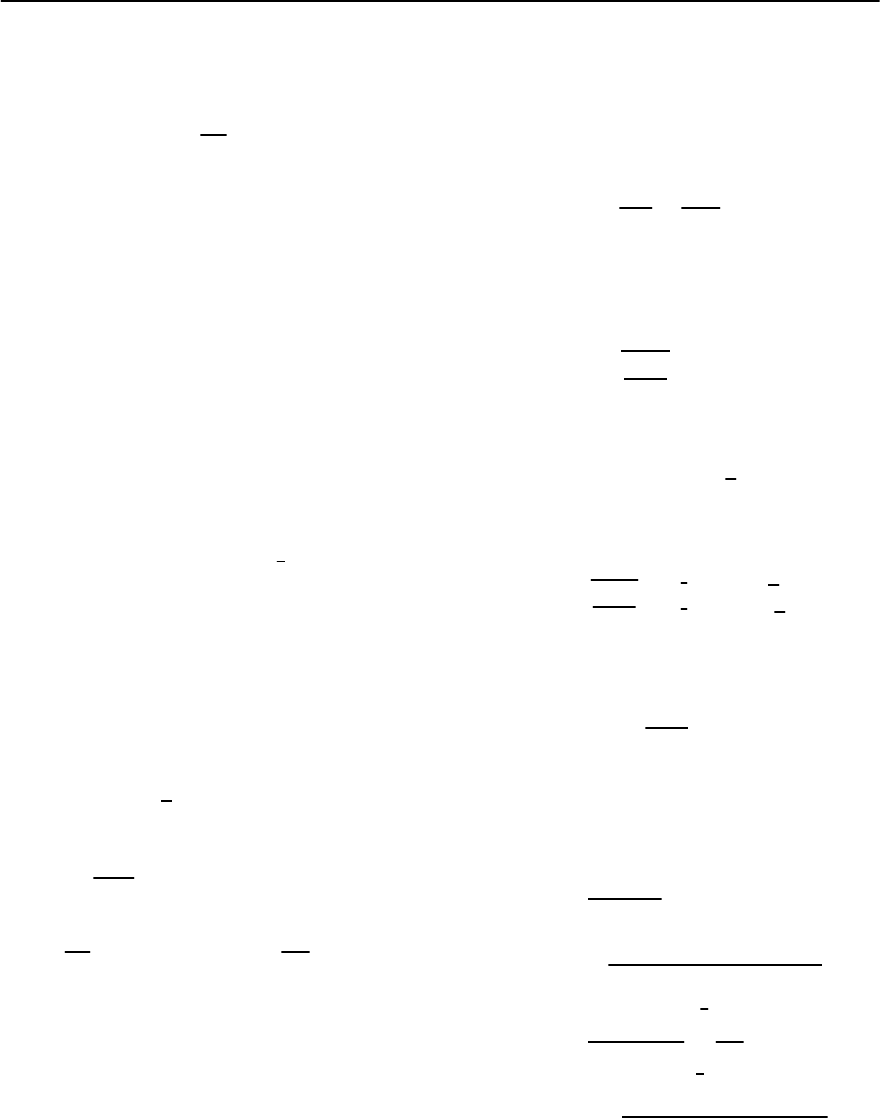
10 Fluctuation Phenomena in Superconductors 401
isotropic spectrum. In this case we choose a plane
wave representation. By using "
p
defined by (10.112)
one has
Bv
{pp
}
= v
p
ı
pp
, v
p
=
@"
p
@p
=2˛T
c
2
p . (10.133)
We do not need to keep the imaginary part of
GL
,
which is necessary to calculate particle-hole asym-
metric effects only. Then the fluctuation conductiv-
ity calculated from (10.133) coincides exactly with
(10.117).
10.4.4 Fluctuation Conductivity of Layered
Superconductors
Let us return to the discussion of our general for-
mula (10.133) for the fluctuation conductivity ten-
sor. A magnetic field directed along the c-axis still
permits separation of variables even in the case of
a layered superconductor. The Hamiltonian in this
case can be written as in (10.71),(10.107):
B
H = ˛T
c
−
2
xy
(∇
xy
−2ieA
xy
)
2
−
r
2
(1 − cos(k
z
s)
.
(10.134)
It it is convenient to work in the Landau representa-
tion, where the summation over {i}is reduced to one
over the ladder of the Landau levels i =0, 1, 2(each
is degenerate with a density H/¥
0
per unit square)
and integration over the c-axis momentum in the
limits of the Brillouine zone. The eigenvalues of the
Hamiltonian (10.134) can be written in the form
"
{n}
= ˛T
c
[ +
r
2
(1 − cos(k
z
s)) + h(2n +1)]
= "
k
z
+ ˛T
c
h(2n +1), (10.135)
where h =
eH
2m˛T
c
was already defined by (10.78). For
the velocity operators one can write
Bv
x,y
=
1
2m
(−i∇−2ieA)
x,y
; Bv
z
=−
˛rs
2
T
c
sin(k
z
s) .
(10.136)
In-Plane Conductivity
Let us start with the calculation of the in-plane com-
ponents.The calculation of the velocity operator ma-
trix elements requires some special consideration.
First of all let us stress that the required matrix el-
ements have to be calculated for the eigenstates of
a quantum oscillator whose motion is equivalent to
the motion of a charged particle in a magnetic field.
Thecommutationrelation for theoscillator’s velocity
components is well known (see [73]):
[Bv
x
,Bv
y
]=i
eH
2m
2
=
i˛T
c
m
h . (10.137)
In order to calculate the necessary matrix elements
let us present the velocity operator componentsin the
form of boson-type creation and annihilation opera-
torsBa
+
,Ba with the commutation relation [Ba,Ba
+
]=1:
Bv
x,y
=
7
˛T
c
h
2m
Ba
+
+Ba
iBa
+
− iBa
.
One can check that the correct commutation relation
(10.137) is fulfilled. Taking into account that
l|Ba|n = n|Ba
+
|l =
√
nı
n,l+1
,
it is seen that the only nonzero matrix elements of
the velocity operator are
l|Bv
x,y
|n =
7
˛T
c
h
2m
√
lı
l,n+1
+
√
nı
n,l+1
i
√
lı
l,n+1
− i
√
nı
n,l+1
.
Using these relations the necessary product of matrix
elements can be calculated:
l|Bv
x
|nn|Bv
x
|l =
˛T
c
h
2m
(lı
l,n+1
+ nı
n,l+1
) .
Its substitution into (10.133) and accounting of the
degeneracy of the Landau levels H/¥
0
=2m˛T
c
h/
givesfor thediagonalcomponent of thein-planecon-
ductivity tensor
xx
(, h, !)=
˛
2
T
2
c
e
2
4m
h
∞
{n,l}=0
% (10.138)
×
(lı
l,n+1
+ nı
n,l+1
)
"
{l}
"
{n}
"
{l}
+ "
{n}
− i
GL
!
=
e
2
(
˛T
c
)
3
h
2
2
s
−
s
dk
z
2
∞
n=0
%
×
n +1
"
n+1
"
n
("
n+1
+ "
n
− i
GL
!)
,
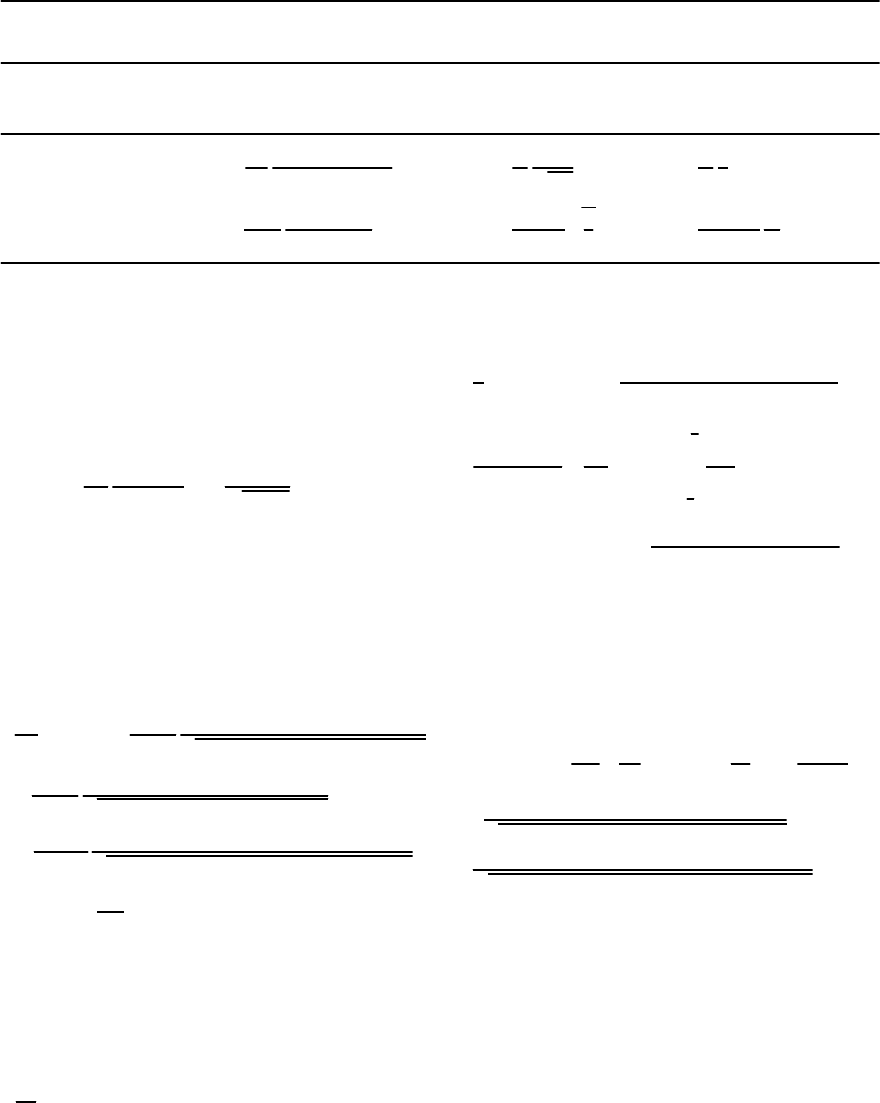
402 A.I. Larkin and A.A.Varlamov
Table 10.2.Results for the magnetoconductivity
h
h r
(3D)
max{, r}h
(2D)
xx
xx
(, h =0)−
e
2
2
8
s
[8( + r)+3r
2
]
[( + r)]
5/2
h
2
e
2
4s
1
√
2hr
e
2
8s
1
h
zz
zz
(, h =0)−
e
2
s
2
8
2
xy
r
2
( + r/2)
[( + r)]
5/2
h
2
3.24e
2
s
2
xy
7
r
h
7(3)e
2
s
2
9
2
xy
r
2
h
2
Expanding the denominatorinto simple fractions we
reduce the problem to the calculation of the c-axis
momentum integral, which can be carried out in the
general case by use of the identity:
2
0
dx
2
1
cos x − z
=−
1
√
z
2
−1
, (10.139)
which is valid for any complex parameter z =1with
the proper choice of the square root branch. Using
it we write the general expression for the in-plane
component of the fluctuation conductivitytensor
xx
(", h, !) =
e
2
h
8s
∞
n=0
(n +1)
1
h − i!
1
√
[ + h(2n + 1)][r + + h(2n +1)]
+
1
h + i!
1
√
[ + h(2n + 3)][r + + h(2n +3)]
(10.140)
−
2h
h
2
+ !
2
1
√
[ + h(2n +2)−i!][r + + h(2n +2)−i!]
.
where ! =
!
16T
c
.
Out-Of Plane Condu ctivity
The situation with the out-of plane component
of paraconductivity turns out to be even simpler
because of the diagonal structure of the Bv
z
{in}
=
−
˛rs
2
T
c
sin(k
z
s) × ı
in
× ı(k
z
− k
z
). Taking into ac-
count that the Landau state degeneracy we write
zz
(, H, !)=
1
2
˛e
2
T
∞
{i,l}=0
%
Bv
˛
{il}
Bv
˛
{li}
"
{i}
"
{l}
("
{i}
+ "
{l}
−2i˛T
c
!)
=
e
2
(
˛T
c
)
3
32
sr
xy
2
h
∞
n=0
s
−
s
dk
z
2
%
×
$
sin
2
(k
z
s)
"
2
n
(k
z
)["
n
(k
z
)−i˛T
c
!]
&
.
The following transformations are similar to the cal-
culationofthein-planecomponent:weexpandthe
integrand into simple fractions and perform the k
z
-
integration by means of the identity (10.139). The
final expression can be written as
zz
(, H, !)=
e
2
64s
sr
xy
2
h
∞
n=0
−
@
@
%
1
+ i!
×
1
√
( + h(2n +1)+)( + h(2n +1)+ + r)
(10.141)
−
1
√
( + h(2n +1)−i!)( + h(2n +1)−i! + r)
|
=0
.
Analysis of the General Expressions
In principle the expressions derived above give an
exact solution for the a.c.(! T) paraconductivity
tensor of a layered superconductor in a perpendicu-
lar magnetic field H H
c2
(h 1) in the vicinity
of the critical temperature ( 1). The interplay of
the parameters r, , ! h entering into (10.141) and
(10.142), as we have seen in the example of fluctua-
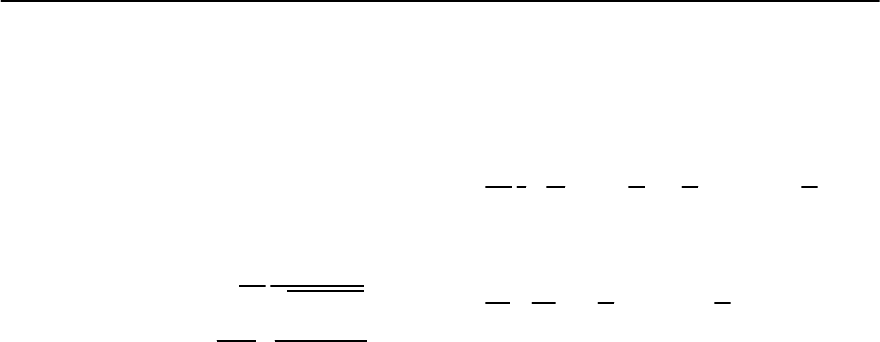
10 Fluctuation Phenomena in Superconductors 403
tion magnetization,yields a varietyof crossover phe-
nomena.
1. The simplest and most important results which
can be derived are the components of the d.c.
paraconductivity (! = 0) of a layered supercon-
ductor in the absence of magnetic field. Keeping
! =0andsettingh → 0 one can change the
summations over Landau levels into integration
and find
xx
(", h → 0, ! =0)=
e
2
16s
1
√
[(r + )]
,
zz
(, h → 0, ! =0)=
e
2
s
32
2
xy
+ r/2
[( + r)]
1/2
−1
.
2. 2. The Aslamazov–Larkin contribution to the
magnetoconductivity can be studied by putting
! = 0 and keeping magnetic field arbitrary. We
will not go into details and just report the re-
sults (following [153] with some revision of the
coefficient in the 3D case).
Here it is worth making an important comment.
The proportionality of the fluctuation magne-
toconductivity to h
2
is valid when using the
parametrization =(T − T
c0
)/T
c0
only. As is
well known, a weak field shifts the critical tem-
perature linearly, which often makes it attrac-
tive to analyze the experimental data by choos-
ing as the reduced temperature parameter
h
=
(T − T
c
(H))/T
c
(H). In this parametrization one
can get a term in the magnetoconductivity lin-
ear in h, which was previously canceled out by
the magnetic field renormalization of the criti-
cal temperature. So it is important to recognize
that the effect of a weak magnetic field on the
fluctuation conductivity cannot be reduced to a
simple replacement of T
c0
by T
c
(H)intheap-
propriate formula without the field. Vice versa,
this effect is exactly compensated by the change
in the functionaldependence of the paraconduc-
tivity in the magnetic field,and finally it contains
thenegativequadraticcontributiononly.
3. Letting the magnetic field go to zero and con-
sidering nonzero frequency of the electromag-
netic field one can find general expressions for
the components of the a.c.paraconductivity ten-
sor. They are cumbersome enough and in the
complete formcan be found,forinstance,in[76].
We recall here the simplified asymptotics for the
Re in the 2D regime only:
Re
xx
(2D)
(r , !) = (10.142)
e
2
16s
1
$
2
!
arctan
!
−
!
2
ln
$
1+
!
2
&&
,
Re
zz
(2D)
(r , !) = (10.143)
e
2
2
8
s
sr
xy
2
1
!
2
ln
$
1+
!
2
&
.
The general formulas (10.141) and (10.142) allow
one to study the different crossovers in the a.c. con-
ductivity of a layered superconductor in the presence
of magnetic fieldsof various intensities.Weleave this
exercise for the reader with some practical interest in
the problem.
10.4.5 Magnetic Field Angular Dependence
of Paraconductivity
We have seen above that in the case of a geometry
with a magnetic field directed along the z-axis many
sophisticated fluctuation features of layered super-
conductors can be studied in the most general form.
Nevertheless,even the attempt to explore the d.c.con-
ductivity in a longitudinal magnetic field (directed
in the xy-plane) [77] or, moreover, with the field di-
rected at some arbitrary angle with the z-axis leads
to the appearance of the vector potential component
in the argument of cos(k
z
s) and the problem requires
a nontrivial calculation of the matrix elements over
the Mathieu functions.
We already learned that at temperatures very near
to the critical one ( r)the3Dfluctuationregime
takes place. Here the size of the Cooper pairs along
the z-axis is so large that the peculiarities of the lay-
ered structure no longer play any role. This means
that only small values of k
z
are important in the k
z
-
integrations, where the cos(k
z
s) in (10.71) can be ex-
panded and the LD functional is reduced to its tra-
ditional GL form with an anisotropic effective mass
tensor:

404 A.I. Larkin and A.A.Varlamov
F[¦ ]=
d
3
r
a|¦ |
2
+
b
2
|¦ |
4
(10.144)
+
3
=1
1
4m
1
i
d
dx
−2eA
¦
2
+
B
2
8
−
H · B
4
.
We will demonstrate below that in this case a scaling
approach provides a direct access to the most gen-
eral results by rescaling the anisotropic problem to
the corresponding isotropic one on the initial level
of the GL approach [78].
Let us suppose that the external field H is chosen
to lie in the y − z plane and makes an angle with
the z-axis. For the sake of simplicity and because
the oxide superconductors are within high accuracy
uniaxial materials, we choose m
x
= m
y
= m
∗
,while
m
−1
z
=2˛Ts
2
r (compare with (10.69)). The effective
anisotropy parameter
2
a
= m
∗
/m
z
=2˛Ts
2
rm
∗
< 1
is introduced. In (10.145) the anisotropy enters only
in the gauge-invariant gradient term, so the sim-
ple rescaling of the coordinate axes: x = x, y =
y, z =
a
z together with the scaling of the vector
potential: A =(
A
x
,
A
y
,
A
z
/
a
) will render this term
isotropic. The magnetic field evidently is rescaled
to B =(
B
x
/
a
,
B
y
/
a
,
B
z
) and the last three terms in
(10.145), describing the magnetic field energy, are
transformed to
ıF[¦ ]=
a
8
d
3
r
1
4m
3
=1
i
d
dx
−2e
A
¦
2
+
B
2
xy
a
+
B
2
z
%
−2
B
xy
· H
xy
a
+
B
z
H
z
%&
.
In short, we have removed the anisotropy from the
gradient term but reintroduced it into the magnetic
energy term. In general it is not possible to make
both terms isotropic in the Gibbs energy simultane-
ously. However, depending on the physical question
addressed, we can neglect fluctuations in the mag-
netic field, as was mostly done above.
Let us demonstrate how the method works for the
example of the d.c. fluctuation conductivity tensor
calculated above for a magnetic field directed along
the z-axis. We restrict our consideration to the 3D
region ( r). One can write the scaling relations
between the electric field and current components
beforeand after the scaling transformationby means
of a conductivity tensor and the anisotropy parame-
ter:
j
x,y
=
j
x,y
, j
z
∼ ev
z
∼
a
j
z
, (10.145)
E
x,y
=
E
x,y
, E
z
∼
@'
@z
∼
1
a
E
z
.
Now let us rewrite the relations between the current
and electric field vectors before and after the scale
transformation
j
˛
=
˛ˇ
E
ˇ
,
j
˛
=
˛ˇ
E
ˇ
.
Comparing them with (10.145) and introducing the
operator of the direct scaling transformation T
˛ˇ
T
˛ˇ
=
10 0
01 0
00
a
%
,
one can write j
˛
= T
˛
j
, E
˛
=(T
−1
)
˛
E
and ex-
press the conductivity tensor as
˛ˇ
= T
˛
T
ˇ
.
Now let us work in the already isotropic coordi-
nate frame. We suppose that initially the magnetic
field was directed perpendicular to layers and now
we rotate it in the x–z plane by the angle
with re-
spect to the initialdirection.The conductivity tensor
will be transformed by the usual matrix law:
˛ˇ
(
)=R
˛
(0)R
T
ˇ
= R
˛
(T
−1
)
&
&
(0)(T
−1
)
ı
R
T
ıˇ
and
˛ˇ
(
)=T
˛
ı
(
)T
ıˇ
= T
˛
R
(T
−1
)
&
&
(0)(T
−1
)
ı
R
T
ı
T
ˇ
,
where
R
˛ˇ
=
⎛
⎝
cos
0−sin
01 0
sin
0cos
⎞
⎠
.
Finally the fluctuation conductivity tensor
˛ˇ
()in
the initial tetragonal system with the magnetic field

10 Fluctuation Phenomena in Superconductors 405
directed at the angle with respect to the direction
normal to layers can be expressed by means of the
effective transformation operator M
˛ˇ
:
˛ˇ
()=M
˛&
(
)
&
(0,
H)M
T
ˇ
(
) ,
with
M
˛ˇ
(
)=T
˛ı
R
ı
(T
−1
)
ˇ
=
⎛
⎝
cos
0−
1
a
sin
01 0
a
sin
0cos
⎞
⎠
.
The angle
can be expressed via the renormalized
magnitude of the magnetic field
H =
H
2
z
+
2
a
H
2
x
:
cos
=
H
z
H
=
cos
cos
2
+
2
a
sin
2
;
sin
=
a
sin
cos
2
+
2
a
sin
2
.
Inthecaseoftheparaconductivityofalayeredsu-
perconductor with the magnetic field applied at an
arbitrary angle the answer can be written in the
general form by means of the three diagonal compo-
nents of conductivity
ii
(0,
H) in the perpendicular
field
H:
˛ˇ
()=
1
R
2
,
a
(10.146)
×
⎛
⎜
⎜
⎝
xx
cos
2
+
zz
sin
2
R
,
a
xy
cos
2
a
2
xx
−
1
2
zz
sin 2
R
,
a
yx
cos R
2
,
a
yy
R
,
a
yx
2
a
sin
2
a
2
xx
−
1
2
zz
sin 2
R
,
a
xy
2
a
sin
xx
4
a
sin
2
+
zz
cos
2
⎞
⎟
⎟
⎠
,
where
R
,
a
=
cos
2
+
2
a
sin
2
.
In the simplest case of a longitudinal field =90
0
:
˛ˇ
(90
0
, H)=
⎛
⎝
zz
/
2
a
0 0
0
yy
yx
a
0
xy
a
xx
2
a
⎞
⎠
.
10.5 Fluctuations Near the
Superconductor–Insulator Transition
10.5.1 Quantum Phase Transition
It is usually supposed that the temperature of the
superconducting transition does not depend on the
concentration of nonmagnetic impurities (Ander-
son’s theorem [79, 80]). Nevertheless, when the de-
gree of disorder is very high Anderson localization
takesplace,andit wouldbe difficultto expect thatun-
der conditions of strong electron localization super-
conductivity can exist, even if there is inter-electron
attraction. This means that at T = 0 the phase
transition takes place with a change of the disorder
strength or carrier concentration. Such a transition
is called a quantum phase transition, since at zero
temperature the classical fluctuations are absent. In-
deed,one can see from (10.7) that in the limit T → 0
the thermal fluctuation Cooper pairs vanish.
In the metallic phase of a disordered system the
conductivity is mostly determined by the weakly de-
caying fermionicexcitations,theirdynamics yielding
the familiar Drude formula (the method accounting
forthe fermionic excitations will be referred to as the
Fermi approach later on). Inside the critical region
the charge transfer due to fluctuation Cooper pairs
turns out to be more important. In some approxima-
tion, the pairs may be considered as Bose particles.
Therefore the approach dealing with the fluctuation
pairs will hereinafter be called the Bose approach.
Let us suppose that at temperature T =0thesu-
perconducting state occurs in a weakly disordered
system. In principle, two scenarios of the develop-
mentofthesituationarepossiblewithanincrease
of the disorder strength: the system at some critical
disorder strength can go from the superconducting
state to the metallic state or to the insulating state.
The first scenario is natural and takes place in the
following cases: if the effective constant of the inter-
electron interactionchanges its sign with the growth
of the disorder; if the effective concentrationof mag-
netic impurities increases together with the disorder
growth; if the pairing symmetry of superconduct-
ing state is nontrivial it can be destroyed even by
the weak disorder level. We will study here the sec-
ond scenario where the superconductor becomes an
406 A.I. Larkin and A.A.Varlamov
insulator with disorder increase. This means that at
some disorder degree range,higher than the localiza-
tion edge when the normal phase no longer exists at
finite temperatures, superconductivity can still sur-
vive. At a first glance this statement seems strange:
what does superconductivity mean if the electrons
are already localized? And if it really can take place
beyond the metallic phase, at what value of disorder
strength and in which way does the superconductiv-
ity finally disappear?
Onehasto bear in mind thatlocalizationisaquan-
tum phenomenonin its natureand with theapproach
to the localization edge the coherence length of local-
ization grows. From the insulator side of the tran-
sition vicinity this means the existence of large scale
regions where delocalized electrons exist. If the en-
ergy level spacing in such regions does not exceed
the value of superconducting gap Cooper pairs still
can be formed by the delocalized electrons of this
region.
The problem can be reformulated in another, al-
ready familiar, way: how does the critical tempera-
ture of the superconducting transition decrease with
the increase of the disorder strength? In the pre-
vious sections we have already tried to solve it by
discussing the critical temperature fluctuation shift.
We have seen that the fluctuation shift of the critical
temperature is proportional to
Gi
(3)
for a 3D su-
perconductor and to Gi
(2)
ln{1/Gi
(2)
} for a 2D super-
conductor. This means that the critical temperature
is not changed noticeably as long as the Ginzburg–
Levanyuk number remains small. So one can ex-
pect the complete suppression of superconductiv-
ity when Gi ∼ 1 only. For further consideration it
is convenient to separate the 3D and 2D cases be-
cause their physical pictures of the superconductor-
insulator transition are quite different.
10.5.2 3D Superconductors
As one can see from Table 10.1 in the 3D case
the Ginzburg–Levanyuk number remains small at
p
F
l ∼ 1: Gi
(3d)
≈
T
c
E
F
1. Nevertheless, approach-
ing the edge of localization, the width of the fluc-
tuation region increases [81]. In the framework of
the self-consistent theory of localization [82] such
growth of the width of the fluctuation region was
found in [83].
Instead of the cited self-consistent theory let us
make some more general assumptions concerning
the character of the metal-insulator (M-I) transition
in the absence of superconductivity[13].We suppose
that in the case of very strong disorder and not very
strong Coulomb interaction the M–I transition is of
second order.The role of“temperature”for this tran-
sition is played by the “disorder strength”, which is
characterized by the dimensionless value g =
p
F
l.
2
.
With its decrease the conductivity of the metallic
phase decreases and at some critical value g
c
tends
to zero as
= e
2
p
F
(g − g
c
)
. (10.147)
This is the critical point of the Anderson (M-I) tran-
sition. We assume that the thermodynamic density
of states remains constant at the transition point.
The electron motion in metallic phase far enough
from the M–I transition has a diffusion character
and the conductivity can be related to the diffu-
sion coefficient D = p
F
l/3m by the Einstein relation:
= e
2
D. One can say that diffusion-like “excita-
tions” with the spectrum !(q)=iDq
2
propagate in
the system. At the point of the M–I transition nor-
mal diffusion terminates and conductivity, together
with D, turns zero. In accordance with scaling ideas,
the diffusion coefficientcan be assumed here to be a
power function of q: D(q) ∼ q
z−2
,withthedynam-
ical critical exponent z2. The anomalous diffusion
excitation spectrum in this case would take the form
! ∼ q
z
.
In the insulating phase (g < g
c
)somelocal,
anomalous diffusion,confined to regions of the scale
, is still possible. It cannot provide charge transfer
throughout the entire system, so D(q =0)=0,but
for small distances (q
−1
) anomalous diffusion
takes place.Analogously, in the metallic phase (gg
c
)
the diffusion coefficient in the vicinity of the transi-
tion has an anomalous dependence on q for q
−1
and weakly depends on it for q
−1
. So one can
conclude that the diffusion coefficient for q
−1
from both sides of the transition has the same q-
dependence as for all q in the transition point. It can
bewrittenintheform

10 Fluctuation Phenomena in Superconductors 407
D(q)=
g
3m
'(q)
p
F
z−2
,
'(x)=
⎧
⎨
⎩
x, x 1
1, x 1, g > g
c
0, x 1, g < g
c
, (10.148)
where the localization length , characterizing the
spatial scale near the transition, grows with the ap-
proach to the transition point like
(g)=
1
p
F
(g − g
c
)
−
z−2
. (10.149)
The critical exponent in this formula is found from
the Einstein relation in the vicinity of the M–I tran-
sition.
At finite temperatures, instead of the critical point
g
c
, a crossover from metallic to insulating behavior
of (g) takes place. The width of the crossover re-
gion is g − g
c
,whereg is determined from the re-
lation D
−2
(g) ∼ E
F
[p
F
(g)]
−z
∼ T (we have used
the second asymptotic of (10.148)). In this region the
diffusion coefficientis
D(T) ∼ T
2
∼
T
p
2
F
E
F
T
2
z
(10.150)
and it depends weakly on g − g
c
. Beyond this region
the picture of the transition remains the same as at
T =0.
Let us consider now what happens to supercon-
ductivityinthe vicinityof the localizationtransition.
In the mean field approximation (BCS) the thermo-
dynamic properties of a superconductor do not de-
pend on the character of the diffusion of excitations.
This should be contrasted with the fluctuation the-
ory, where such a dependence clearly exists. We will
show that the type of superconducting transition de-
pends on the dynamical exponent z.Ifz3,the transi-
tion to superconductivity occurs on the metallic side
of the localization transition (we will refer to such a
transition as an S–N transition).If z < 3, the transi-
tion to superconductivity occurs from the insulating
state directly (S–I transition).
Letus study how the superconducting fluctuations
affect the transition under discussion.In spirit of the
GL approach fluctuation phenomena in the vicinity
of the transition can be described in the framework
of the GL functional (10.27). The coherence length
in the metallic region, far enough from the Ander-
son transition, was reported in Introduction to be
equal
2
=
c
l =0.42D/T.In the vicinity of the M–I
transition we still believe in the diffusive character
of the electron motion resulting in the pair forma-
tion. The only difference from the previous consid-
eration is the anomalous character of the quasipar-
ticle diffusion. So in order to describe the supercon-
ducting fluctuations simultaneously near supercon-
ducting (in temperature) and Anderson (in g) tran-
sitions let us use the GL functional (10.27) with the
k-dependent diffusion coefficient (10.148).
The value of Gi can be estimated from the expres-
sion forthe fluctuation contributionto heat capacity
(10.30)taken at ∼ Gi,where the fluctuation correc-
tion reaches the value of the heat capacity jump:
1 ∼
T
d
3
q
TGi + D(q)q
2
2
, (10.151)
withT T
c
.Let us approach theM–I transition from
themetallic side.If weare far enoughfromtransition,
Gi is small and the integral in (10.151)is determined
by the region of small momenta D(q)q
2
TGi:
Gi ∼
T
2
D
3
(q =0)
. (10.152)
Two scenarios are possible: Gi becomes of the order
of 1 in the metallic phase, or it remains small up to
the crossover region, where finally reaches its satu-
ration value. In the first case we can use the second
asymptotic of (10.148) for D(q) and find:
Gi ∼
T
c
E
F
(p
F
)
3z−6
. (10.153)
One can see that Gi becomesoftheorderof1
at p
F
M
∼
(
E
F
/T
)
1
3z−6
. Comparing this value with
p
F
(g) ∼
(
E
F
/T
)
1/z
at the limit of the crossover re-
gion we see that for z3 the first scenario is realized.
Concluding our discussion of the first scenario we
can see that the superconducting critical tempera-
ture goes to zero at =
M
, still in the metallic phase,
so at T = 0 a superconductor-normal phase (S–N)
type quantum phase transition takes place.
408 A.I. Larkin and A.A.Varlamov
The second scenario takes place for z < 3whenGi
remains small even at the edge of crossover region,
reaching there the value
Gi ∼
T
c
E
F
2(3−z)
z
1 . (10.154)
In the crossover region the diffusion coefficient, and
hence Gi, almost do not vary. This is why the temper-
ature of superconducting transition remains almost
frozen with further increase of disorder driving the
system through the Anderson transition. The abrupt
growth of Gi and decrease of T
c
take place when
the system finally goes from the crossover to the in-
sulating region. In the insulator phase the diffusion
coefficient D(q l
−1
) = 0 and from (10.151) one can
find for Gi:
Gi ∼
E
F
T
c
1
(p
F
)
3/2
. (10.155)
Comparing this result with the Table 10.1 it is easy
to see that it coincides with the Ginzburg–Levanyuk
number for a zero-dimensional granule of size
(T). Hence we see that in the second scenario
the Ginzburg number reaches 1 and, respectively,
T
c
→ 0atp
F
I
∼
E
F
T
c
1/3
, which is far enough
from the M–I transition point. This is why in this
case one can speak about the realization at T =0ofa
superconductor-insulator (S–I) type quantum phase
transition. The scale
I
determines the size of the
“conducting”domains in the insulating phase, where
the level spacing reaches the order of the supercon-
ducting gap. It is evident that in the domain of scale
I
superconductivity cannot be realized.
In the vicinity of a quantum phase transition one
can expect the appearance of nonmonotonic depen-
dencies of the resistance on temperature and mag-
netic field. Indeed, starting from the zero resistance
superconducting phase and increasing temperature
from T = 0, the system passes through the local-
ization region, where the resistance is high, to high
temperatures where some hopping charge transfer
will decrease the resistance again. The analogous
speculations are applicable to the magnetic field ef-
fect:firstthe magneticfield“kills”superconductivity
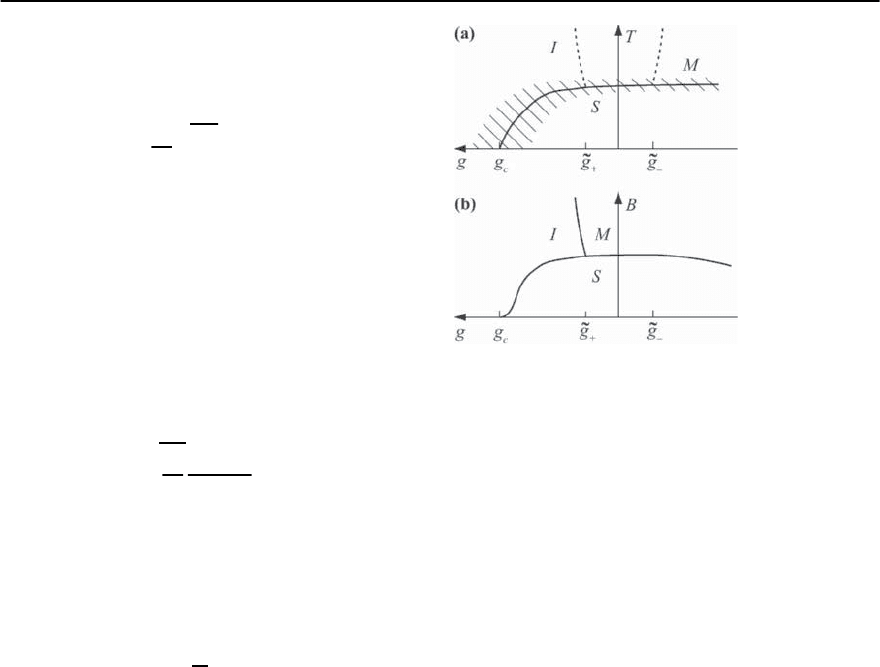
Fig. 10.5. Phase diagram in the temperature-disorder plane
for a 3D superconductor
and increases the resistance, then it destroys local-
ization and decreases it. The phase diagram in the
(T, g) plane has the form sketched in Fig. 10.5. For
g
I
= g
c
−(T
c
/E
F
)
3(z−2)/
,an S–I transition takes place
at T = 0. Increasing the temperature from T =0in
the region 0 g g
I
we remain in the insulating
phase with exponential dependence of resistance on
temperature. For g
I
g g
−
at low temperatures
0 ≤ T < T
c
(g) the system stays in the supercon-
ducting state, which goes to the insulating phase at
higher temperatures. In the vicinity of the Ander-
son transition (g
−
g g
+
) the superconducting
stategoeswithgrowthofthetemperaturetosome
crossover metal-insulator state which is character-
ized by a power decrease of the resistivity with the
increase of temperature. Finally at g
c
g the super-
conducting phase becomes of the BCS type and at
T = T
c
it goes to a metallic phase.
The phase diagram in the magnetic field-disorder
plane is similar to that in the (T, g) plane with the
only difference that at T = 0 there is no crossover
region, instead a phase transition takes place.
10.5.3 2D Superconductors
Preliminaries
As was demonstrated, according to the conventional
theory of paraconductivity, the sheet conductivity
in the vicinity of the superconducting transition is
given by a sum of the electron residual conduc-
