Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


10 Fluctuation Phenomena in Superconductors 429
are suppressed by the square of the barrier trans-
parency and the DOS contribution, which has a
weaker temperature dependence but depends only
linearly on the barrier transparency.
10.8 Manifestation of Fluctuations in
Various Properties
In this section we will demonstrate the applications
of themicroscopictheoryof fluctuations.Thelimited
volume does not permit us to deliver the systematic
review of the modern theory here and we restrict
ourselves by only presenting the several representa-
tive recent studies.
It is necessary to underline that the comparison of
the results offluctuation theory with the experimen-
tal findings on HTS materials has to be considered
sooner in a qualitative context than in a quantitative
context. Indeed, as is clear now, the superconductiv-
ity in the most of HTS compounds has the nontrivial
symmetry. Moreover, as was discussed in the previ-
ous section, these compounds are rather clean than
dirty. Both these complications can be taken into ac-
count (see for example [97,111]), but this was not
done in the majority of the cited papers.
10.8.1 The Effects of Fluctuations
on Magnetoconductivity
The experimental investigations of the fluctuation
magnetoconductivity are of special interest first be-
cause this physical value weakly depends on the nor-
mal state properties of superconductor and second
due to its special sensitivity to temperature and mag-
netic field. The role of AL contribution for both
the in-plane and out-of-plane magnetoconductivi-
ties was studied above in the framework of the phe-
nomenological approach. The microscopic calcula-
tions of the other fluctuation corrections to the in-
plane magnetoconductivity conductivity show that
the MT contribution has the same positive sign and
temperature singularity as the AL one. In the case
of weak pair-breaking it can even considerably ex-
ceed the latter. The negative DOS contribution, like
in the case of the zero-field conductivity,turnsout to
be considerably less singular and many authors (see,
e.g. [125–136]) successfully explained the in-plane
magnetoresistance data in HTS using the AL and MT
contributions only [137–140].
Turning to the out-of-plane magnetoconductivity
of a layered superconductor one can find a quite dif-
ferent situation. Both the AL and MT contributions
here turn out to be of the second order in the in-
terlayer transparency, and this circumstance makes
a less singular DOS contribution, which however
remains of first order in transparency, to be com-
petitive with the main terms [142]. The large num-
ber of microscopic characteristics involved in this
competition, like the Fermi velocity, interlayer trans-
parency,phase-breaking and elastic relaxation times,
gives rise to the possibility of occurrence of different
scenarios for various compounds. The c-axis mag-
netoresistance of a set of HTS materials shows a
very characteristic behavior above T
c0
.Incontrast
to the ab-plane magnetoresistance which is posi-
tive at all temperatures, the magnetoresistance along
the c-axis has been found in many HTS compounds
(BSSCO [143,145–147],LSSCO [148],YBCO[149] and
TlBCCO[150]) to havea negativesign not too closeto
T
c0
and turn positive at lower temperatures. We will
show how this behavior finds its explanation within
the fluctuation theory [97].
We consider here the effect of a magnetic field
parallel to the c-axis. In this case both quasiparticles
and Cooper pairs move along Landau orbits within
the layers. The c-axis dispersion remains unchanged
from the zero-field form.Inthe chosen geometry one
can generalize the zero-field results reported in the
previous section to finite field strengths simply by
the replacement of the two-dimensional integration
over q by a summation over the Landau levels
d
2
q
(2)
2
→
H
¥
0
n
=
h
2
(2)
n
(let us recall that
(2)
=
2
xy
). So the general expres-
sions for all fluctuation correctionsto the c-axis con-
ductivityin a magnetic field can be simply written in
the form [97]:
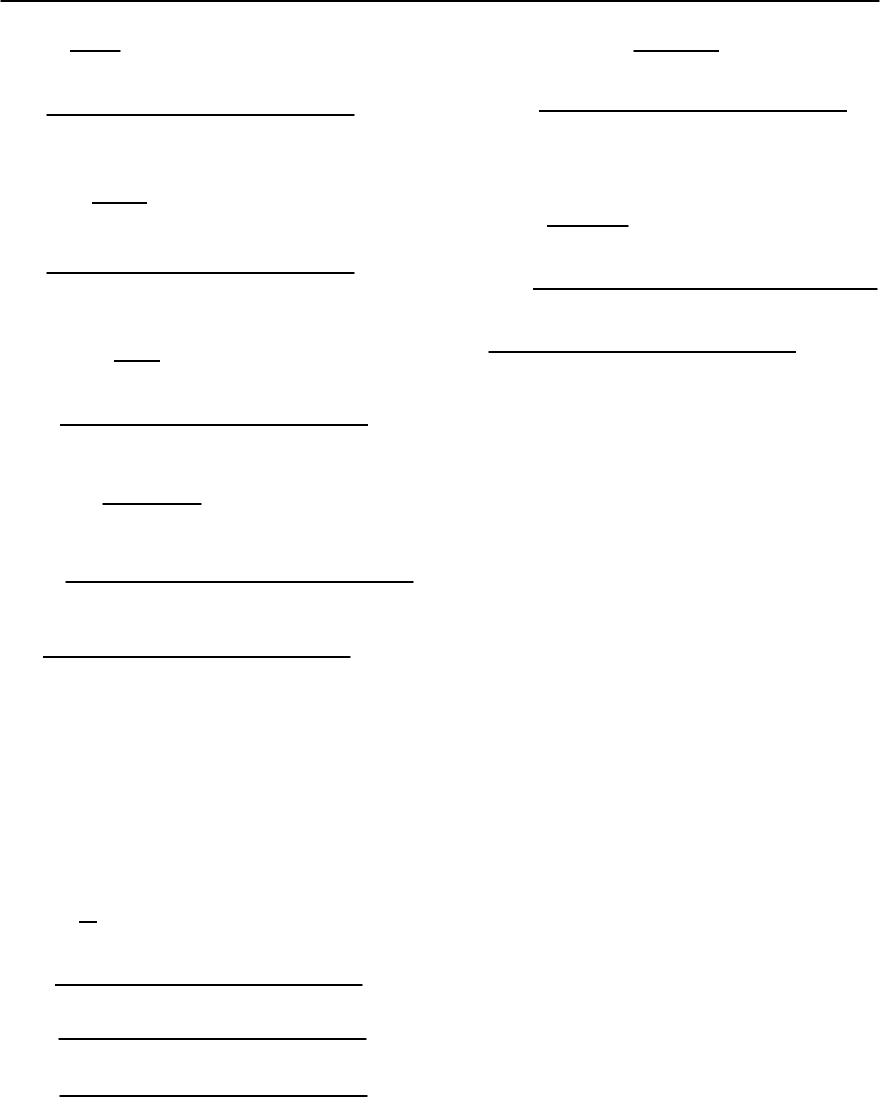
430 A.I. Larkin and A.A.Varlamov
AL
zz
=
e
2
sr
2
h
64
2
xy
(10.217)
∞
n=0
1
{[ + h(2n + 1)][r + + h (2n +1)]}
3/2
,
DOS
zz
=−
e
2
srh
8
2
xy
(10.218)
1/h
n=0
1
{[ + h(2n + 1)][r + + h (2n +1)]}
1/2
,
MT(reg)
zz
=−
e
2
s ˜h
4
2
xy
(10.219)
∞
n=0
+ h(2n +1)+r/2
{[ + h(2n + 1)][r + + h (2n +1)]}
1/2
−1
,
MT(an)
zz
=
e
2
sh
8
2
xy
(" −
'
)
(10.220)
∞
n=0
'
+ h(2n +1)+r/2
=
[(
'
+ h(2n + 1)][
'
+ h(2n +1)+r)]
>
1/2
−
+ h(2n +1)+r/2
{[ + h(2n + 1)][r + + h (2n +1)]}
1/2
.
For the in-plane component of the fluctuation
conductivity tensor the only additional problem ap-
pears in the AL diagram, where the matrix elements
of the harmonic oscillator type,originatingfrom the
B
(q
) blocks, have to be calculated. How to do this
was demonstrated in detail in Sect. 10.4. The other
contributions are essentially analogous to their c-
axis counterparts:
AL
xx
=
e
2
4s
∞
n=0
(n + 1) (10.221)
1
{[ + h(2n + 1)][r + + h (2n +1)]}
1/2
−
2
{[ + h(2n + 2)][r + + h(2n +2)]}
1/2
+
1
{[ + h(2n + 3)][r + + h(2n +3)]}
1/2
,
DOS
xx
+
MT(reg)
xx
=−
e
2
h( + ˜)
2s
(10.222)
×
1/h
n=0
1
{[ + h(2n + 1)][r + + h(2n +1)]}
1/2
,
and
MT(an)
xx
=
e
2
h
4s( −
'
)
(10.223)
×
∞
n=0
1
=
[(
'
+ h(2n + 1)][
'
+ h(2n +1)+r)]
>
1/2
−
1
{[ + h(2n + 1)][r + + h (2n +1)]}
1/2
.
These resultscan,in principle,already be used for nu-
merical evaluations and fitting of the experimental
data, which was indeed successfully done in a series
of papers [149–151].
The detailed comparison of the cited results with
the experimental data [149,152], especially in strong
fields, raised the problem of regularization of the
DOS contribution. If in the absence of the mag-
netic field its ultra-violet divergence was success-
fully cut off at q ∼
−1
, in the case under consid-
eration the cut-off parameter depends on the mag-
netic field and makes the fitting procedure ambigu-
ous. The solution of this problem was proposed
in [153], where the authors calculated the differ-
ence
DOS
zz
=
DOS
zz
(h, )−
DOS
zz
(0, )applyingto
(10.219) and (10.222) the same trick already used
in Sect. 10.2 for the regularization of the free en-
ergy in magnetic field (10.79). The corresponding
asymptotics for all out-of-plane fluctuation contri-
butions are presented in Table 10.3: The procedure
described gives an excellent fitting up to very high
fields [154], which is shown in Fig. 10.13. Let us start
the analysis from the 2D case (r ). One can see
that here the positive DOS contribution to magne-
toconductivity turns out to be dominant. It grows
as H
2
up to H
c2
() and then crosses to a slow log-
arithmic asymptote. At H ∼ H
c2
(0) the value of
DOS
zz
(h ∼ 1, )=−
DOS
zz
(0, ), which means the
total suppression of the fluctuation correction in
such a strong field. The regular part of the Maki–
Thompson contribution does not manifest itself in

10 Fluctuation Phenomena in Superconductors 431
Table 10.3.Results for the out of plane contribution of the fluctuations to the conductivity
h h r (3D)
DOS
zz
e
2
s
32
5
2
xy
r( + r/2)
[( + r)]
3/2
h
2
0.428
e
2
s
16
2
xy
r
7
h
r
MT(reg)
zz
e
2
s ˜
32
6
2
xy
r
2
[( + r)]
3/2
h
2
0.428
e
2
s ˜
8
2
xy
r
7
h
r
−
AL
zz
e
2
s
2
8
2
xy
r
2
( + r/2)
[( + r)]
5/2
h
2
AL
zz
(0, )−
3.24e
2
s
2
xy
7
r
h
−
MT(an)
zz
min{, r}
'
e
2
s
32
7
2
xy
r
2
[( + r)]
2
h
2
MT(an)
zz
(0, )−
e
2
s
32
2
xy
7
r
'
−
MT(an)
zz
'
min{, r}
e
2
s
32
7
2
xy
√
r
3/2
'
h
2
MT(an)
zz
(0) −
3.24e
2
s
64
2
xy
7
r
h
max{, r}h (2D)
DOS
zz
e
2
s
8
2
xy
r ln
√
h
√
+
√
+ r
MT(reg)
zz
−
MT(reg)
zz
(0, )−
2
e
2
s ˜
2
8
2
xy
r
2
h
−
AL
zz
AL
zz
(0, )−
7(3)e
2
s
2
9
2
xy
r
2
h
2
−
MT(an)
zz
min{, r}
'
MT(an)
zz
(0, )−
3
2
e
2
s
2
8
2
xy
max{r,
'
}
h
−
MT(an)
zz
'
min{, r}
MT(an)
zz
(0, )−
3
2
e
2
s
2
8
2
xy
(r + )
h
this case while the AL term can compete with the
DOS one in the immediate vicinity of T
c
,wherethe
small anisotropy factor r can be compensated by the
additional
3
in thedenominator.The anomalous MT
contribution can contributein the case of small pair-
breaking only, which is opposite to what is expected
in HTS.
In the 3D case ( r) the behavior of the magne-
toconductivity is more complex. In weak and inter-
mediate fields the main,negative, contribution to the
magnetoconductivity occurs from the AL and MT
terms. At H ∼ H
c2
()(h ∼ ) the paraconductivity
is already considerably suppressed by the magnetic
field and the h
2
-dependence of the magnetoconduc-
tivity changes through the
r
h
tendency to the high
field asymptote −
(fl)
zz
(0, ). In this intermediate re-
gion of fields ( h r), side by side with the
decrease (∼
r
h
) of the main AL and MT contribu-
432 A.I. Larkin and A.A.Varlamov
Fig. 10.13. Magnetoconductivityversus temper-
ature at 27 T for an underdoped Bi-2212 single
crystal. The solid line represents the theoretical
calculation. The symbols are the experimental
magnetoconductivity
zz
(B c I) [154]
tions,the growthof the still relatively small DOS term
takes place.At the upper limit of this region (h ∼ r)
its positive contribution is of the same order as the
AL one and at high fields (r h 1) the DOS con-
tribution determines the slow logarithmic decay of
the fluctuation correction to the conductivity, which
is completely suppressed only at H ∼ H
c2
(0). The
regular part of the Maki–Thompson contribution is
not of special importance in the 3D case. It remains
comparable with the DOS contribution in the dirty
case at fields h r, but decreases rapidly (∼
r
h
)at
strong fields ( h r), in the only region where the
robust
DOS
c
(h, ) ∼ ln
h
r
shows up surviving up to
h ∼ 1.
The temperature dependence of the different fluc-
tuation contributions to the magnetoconductivity
calculated for an underdoped Bi-2212 single crystal
at the magnetic field 27 T is presented in Fig. 10.14.
The formulas for the in-plane magnetoconductiv-
ity are presented in Table 10.4: Analyzing the table
one can see that in almost all regions the negative
AL and MT contributions govern the behavior of in-
plane magnetoconductivity.Nevertheless, similar to
the c-axis case, the high field behavior is again deter-
mined by the positive logarithmic (
DOS
xx
+
MT(reg)
xx
contribution, which is the only one to survive in
strong field. It is important to stress that the sup-
pression of the DOS contributionby a magnetic field
takes place very slowly. Such robustness with respect
to the magnetic field is of the same physical origin
as the slow logarithmic dependence of the DOS-type
corrections on temperature.
Another important problem that appears in the
fitting of the resistive transition shape in relatively
strong fields with the fluctuation theory is the much
larger broadening of the transition than predicted
by the Abrikosov–Gor’kov theory [155]. Kim and
Gray[96] explainedthebroadening of thec-axis peak
with increasing magnetic field in terms of Josephson
coupling, describing a layered superconductor as a
stack of Josephson junctions. In [69, 156] the self-
consistent Hartree approach was proposed for the
extension of fluctuation theory beyond the Gaussian
approximation. It results in the considerable shift of
T
c
(H) toward low temperatures with a correspond-
ing broadening of the transition. The renormalized
reduced temperature ˜"
h
is determined according to
the self-consistent equation [69]:
"
h
= ˜"
h
−4Gi
(
2
)
h (10.224)
×
1/h
n=0
1
[( ˜"
h
+ hn)( ˜"
h
+ h(n +1)+r)]
1/2
.
The authors of [157], following the procedure pro-
posed by Dorsey and Ullah [69], modified (10.218)–
(10.224) to account for (10.225). As a result they
succeeded to fit quantitatively both in-plane resis-
tivity transition and the transverse resistivity peak
for BSCCO films strongly broadened by the applied
magnetic field.
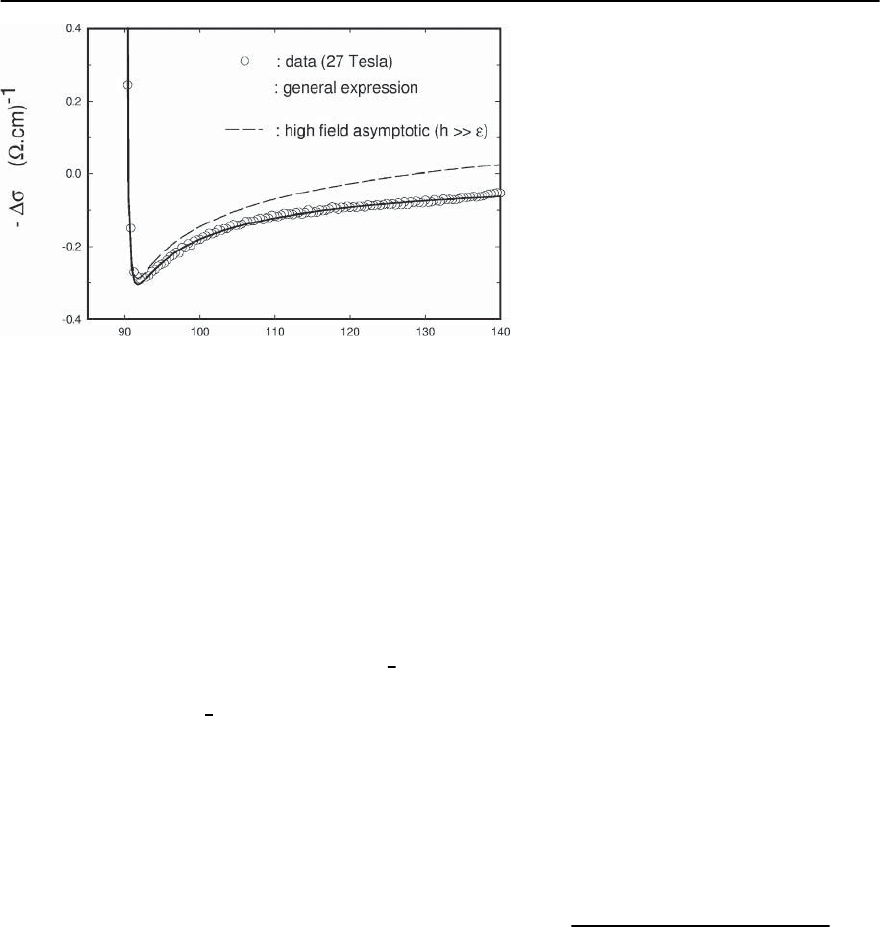
10 Fluctuation Phenomena in Superconductors 433
Fig. 10.14. Decomposition of the calculation of
total theoretical magnetoconductivity for an
underdoped Bi-2212 single crystal at 27 T. The
inset shows the regular and anomalous parts
of the MT contribution that are too small to be
presented on the same scale as the AL and DOS
contributions[154]
Table 10.4.In-plane magnetoconductivity contributions due to fluctuations
h
h r;max{, r}h
AL
xx
−
e
2
2
8
s
[8( + r)+3r
2
]
[( + r)]
5/2
h
2
−
AL
xx
(0, )+
e
2
4s
1
√
2hr
;
−
AL
xx
(0, )+
e
2
8s
1
h
MT(an)
xx
(min{, r}
'
)
−
e
2
32
5
s
( + r/2)
[( + r)]
3/2
h
2
−
MT
xx
(0, )+
e
2
8s
1
'
ln
√
'
√
2h +
=
√
2h + r
MT(an)
xx
(
'
min{, r})
−
e
2
32
5
s
1
3/2
r
1/2
h
2
−
MT
xx
(0, )+
0.2e
2
s
1
√
hr
;
−
MT
xx
(0, )+
3
2
e
2
32s
1
h
(
DOS
xx
+
MT(reg)
xx
e
2
( + ˜)
32
7
s
( + r/2)
[( + r)]
3/2
h
2
0.428
e
2
( + ˜)
2
6
s
7
h
r
;
e
2
( + ˜)
32s
ln
√
h
(
√
+
√
+ r)
10.8.2 Fluctuations Far from T
c
or in Strong Magnetic
Fields
As was mentioned above the role of fluctuations is
especially pronounced in the vicinity of the critical
temperature.Nevertheless for some phenomena they
can still also be considerable far from the transition.
In these cases the GL theory is certainly unapplica-
blesincetheshort-waveanddynamicalfluctuation
contributions have to be taken into account. It can
be done in the microscopic approach, which we will
demonstrate by several examples.
434 A.I. Larkin and A.A.Varlamov
Fluctuation Magnetic Susceptibility Far from Transition
The given above qualitative estimations (10.57)–
(10.64) for the fluctuation diamagnetic susceptibil-
ity,based on the Langevin formula,demonstrate that
even at high temperatures T T
c
it turns to be of
the order of
P
forclean 3D superconductorsand no-
ticeably exceeds this value for 2D systems. In order
to develop the microscopic theory [29,158,159] let us
start from the general expression for free energy in
the one-loop approximation:
F = T
§
k
Tr{ln[1 − g¢(§
k
, r, r
)]}, (10.225)
where g is the effective interaction constant related
with the transition critical temperature by (10.173).
This approximation corresponds to the ladder one
(see (10.166)) for the fluctuation propagator. The
polarization operator ¢(§
k
, r, r
) is determined by
expression (10.167). In the case of an applied mag-
netic field the homogeneity of the system is lost and
¢(§
k
, r, r
) depends not on the space variable dif-
ference r− r
, but on each one separately. Expanding
¢(§
k
, r, r
) one can express the magnetic suscepti-
bility of a layered superconductor in a weak mag-
netic field perpendicular to the layers in terms of the
derivatives ¢
x
=
@
@q
x
¢(q) [29]:
=−
@
2
F
@H
2
(10.226)
=−
2
3
e
2
T
§
k
d
3
q
(2)
3
L
3
¢
x
(¢
x
¢
yy
− ¢
y
¢
xy
) .
The final expressions for thefluctuationdiamagnetic
susceptibility in the clean and dirty cases for wide
range of temperatures can be written as:
(2)
fl
(T)=
P
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0.05
p
F
s
P
E
F
T
1
ln
3
(T/T
c
)
,
−1
T !
D
2
2
3
ln ln
1
T
c
−lnln(T/T
c
)
, T
c
T
−1
,
(10.227)
(2)
fl
(T)=
0.05
p
F
s
P
E
F
T
1
ln
3
(T/T
c
)
. (10.228)
Letusstressthattheseresultsarealsovalidfor
the fluctuation diamagnetism of a normal metal
with g0, if by T
c
one uses the formal value T
c
∼
E
F
exp(
1
g
).
Fluctuation Magnetoconductivity Far from Transition
Let us discuss the conductivity of the 2D electron sys-
tem with impurities in a magnetic field at low tem-
peratures. Even in the absence of the field the effects
of quantum interference of the noninteracting elec-
tronsintheir scatteringsonelasticimpuritiesalready
results in the appearance of a nontrivial temperature
dependence of the resistance. This result contradicts
the statement of the classical theory of metals re-
quiring the saturation of the resistance at its resid-
ual value at low temperatures. In a superconductor
above the critical temperature this, so-called weak
localization (WL), effect is amplified by the Andreev
reflection of electrons on the fluctuation Cooper pair
leading to appearance of the MT correction to the
conductivity. The characteristic feature of both the
MT and WL corrections is their extreme sensitivity
to the dephasing time
'
and to weak magnetic fields.
Beyond the GLregion (T T
c
)theMTcorrection
is determined by the same diagram 2 in Fig. 10.9 but
now the dynamic (§
k
= 0) and short-wave-length
(q ∼
−1
) fluctuation modes have to be taken into
account. The corresponding calculations were per-
formed in [98,160] and the result can be written in
the form:
ı
WL+MT
=
e
2
2
2
˛ − ˇ(T)
Y
§
L
'
, (10.229)
where we introduced the effective Larmour fre-
quency for the diffusion motion §
L
=4DeH with
the diffusion coefficient D
28
and the function
Y
(
x
)
=lnx +
1
2
+
1
x
=
⎧
⎨
⎩
x
2
24
, x 1
ln x, x 1
.
(10.230)
28
A comparison of the expressions (10.78), (10.135) and (10.229) relates the Larmour frequency with the dimensionless
field: h = §
L
/2T
c
introduced in Sect. 10.2 and the diffusion coefficient with the phenomenological GL constants
D =1/m˛.
10 Fluctuation Phenomena in Superconductors 435
The first term in this formula corresponds to the
WL contribution (˛ =1ifthespin-orbitinteraction
of the electrons with the impurities is small while
in the opposite limiting case ˛ =−1/2), the sec-
ond describes the MT contribution to magnetocon-
ductivity. The function ˇ[ln(T/T
c
)] was introduced
in [160]. At T → T
c
ˇ(x)=1/x and (10.229) re-
duces to the already studied MT correction in the
vicinity of critical temperature. For T T
c
ˇ(x)=
1/x
2
and the MT contribution gives a logarithmi-
cally small correction to the WL result. Its zero-field
value, being proportional to ln
−2
(T/T
c
), decreases
with the growth of the temperature faster than both
the AL contribution (in the dirty case ı
AL
∼
1/ ln(T/T
c
)) and the especially slow DOS contribu-
tion
(
ı
DOS
∼ ln ln(1/T
c
) − ln ln(T/T
c
)
)
(see [98,
99]).
It worth mentioning that for the region of temper-
atures T T
c
, analogous to (10.227)–(10.228), the
result (10.229) can be applied both to superconduct-
ing and normal metals (g0), if in place of the crit-
ical temperature the formal value T
c
∼ E
F
exp(
1
g
)
is undermined. The interplay of the localization and
fluctuation corrections was extensively studied (see,
for example, [161–165]).
Fluctuations in Magnetic Fields near H
c2
(0)
Asone can see from (10.222)–(10.224),inthe vicinity
of the upper critical field H
c2
(T)thefluctuationcor-
rections diverge as
−1
h
forthe2Dcaseandas
−1/2
h
for
the 3D case
29
(it is enough to keep just the terms with
n = 0 in these formulas). This behavior is also pre-
served in strong magnetic fields, but the coefficients
undergo changes.A case of special interest is T T
c
(which means H → H
c2
(0)), which represents an
example of a quantum phase transition [166]. Mi-
croscopic analysis of the magnetoconductivity per-
mits us tostudy the effect of fluctuations inmagnetic
fields of the order of H
c2
(0), where the GL functional
approach is inapplicable.
We restrict our study to the case of a dirty metal
(T 1). In this limit |˜!
n+
− ˜!
−n
|≈
−1
and the
Green function correlator (10.169) can be written in
the form
P(q, "
1
, "
2
)=2
2
(−"
1
"
2
) (10.231)
×
−1
− |"
1
− "
2
| −
B
Dq
2
.
Expressing ¢(q, §
k
)intermsofP(q, "
1
, "
2
)by
means of (10.187) and using the definition of the
critical temperature one can find an explicit formula
for the fluctuation propagator:
L
−1
(q, §
k
)=−g
−1
+ ¢(q, §
k
) (10.232)
=−
$
ln
T
T
c
+
1
2
+
|§
k
| +
B
Dq
2
4T
%
−
1
2
&
.
The prominent characteristic of this expression is
that it is valid even relatively far from the critical
temperature (for temperatures T min{
−1
, !
D
})
and for |q|l
−1
, |§
k
|!
D
.
One can rewrite this expression in a magnetic field
applied along the c-axis in the Landau representation
by simply replacing
B
Dq
2
⇒ §
L
(n +1/2) [158]:
L
−1
n
(q
z
, §
k
)=−
ln
T
T
c
+
1
2
+
|§
k
|
4T
(10.233)
+
§
L
(n +1/2) + 4J
2
sin
2
q
z
s/2
4T
%
−
1
2
&
.
In the case of arbitrary temperatures and mag-
netic fields the expression for the AL contribution to
the conductivity takes the form:
Q
AL
xx
(!
)=
−4e
2
T
§
k
∞
{n,m}=0
B
n,m
(§
k
+ !
, §
k
)L
m
(§
k
)
×B
m,n
(§
k
, §
k
+ !
)L
n
(§
k
+ !
) (10.234)
(we have restricted our consideration to the 2D case).
The expression for B
n,m
(§
k
, !
) can be rewritten as
B
n,m
(§
k
+ !
, §
k
) = (10.235)
−4
2
D
(2)
eH(n +1)ı
m,n+1
+
√
eHnı
m,n−1
×T
"
i
n
("
i
+ !
, §
k
− "
i
)
m
("
i
, §
k
− "
i
)
with
m
("
1
, "
2
)=
1
Ÿ
(
−"
1
"
2
)
|"
1
− "
2
| + §
L
(m +1/2)
. (10.236)
29
h
is the renormalized by the magnetic field reduced temperature
h
= + h

436 A.I. Larkin and A.A.Varlamov
The critical field H
c2
(T) is determined by the
equation L
−1
0
(q
z
=0, §
k
= 0) = 0. This is why
in the vicinity of H
c2
(T)thesingularcontribution
to (10.234) originates only from the terms with
L
0
(0, §
k
). The frequency dependencies of the func-
tions B
n,m
(§
k
+ !
, §
k
)andL
1
(§
k
) are weak al-
though we cannot omit them. It is enough to restrict
ourselves to the linear approximation in their fre-
quency dependencies. If the temperature T T
c0
the sum over frequencies in (10.235) can be approx-
imated by an integral. Transforming the boson fre-
quency §
k
summation to a contour integration as
was done above and making the analytic continua-
tion in the external frequency !
one can get an ex-
plicit expression for the d.c. paraconductivity. In the
same spirit the contributionsof all other diagrams in
Fig. 10.9 which contribute to fluctuation conductiv-
ity in the case under discussion are calculated side
by side with the AL one. The final answer can be
presented in the form:
ı
tot
=
2e
2
3
2
−ln
T
c0
2 T
+
3
E
T
T
c0
H
c2
(T)
H − H
c2
(T)
+
T
c0
2
E
T
H − H
c2
(T)
H
c2
(T)
(10.237)
+4
T
c0
2
E
T
H
c2
(T)
H − H
c2
(T)
×
T
c0
2
E
T
H − H
c2
(T)
H
c2
(T)
−1
,
where
E
is the Euler constant. Let us consider some
limiting cases. If the temperature is relatively high
T/T
c0
(
H − H
c2
(T)
)
/H
c2
(T), we obtain the fol-
lowing formula for the fluctuation conductivity:
ı =
2
E
e
2
2
T
T
c0
H
c2
(T)
H − H
c2
(T)
. (10.238)
If HH
c2
(0), we can introduce T
c
(H) and rewrite
(10.238) in the usual way
ı =
3e
2
2
E
2
T
c0
T − T
c
(H)
. (10.239)
If HH
c2
(0), in the low-temperature limit T/T
c0
(
H − H
c2
(T)
)
/H
c2
(T)wehave
ı =−
2e
2
3
2
ln
H
c2
(T)
H − H
c2
(T)
. (10.240)
One can see, that even at zero temperature a loga-
rithmic singularity remains and the corresponding
correction is negative.It results from all three fluctu-
ation contributions, although the DOS one exceeds
the others by numerical factor. Let us recall that in
the case of the c-axis conductivityof a layered super-
conductor, or in granular superconductors above T
c
,
the DOS contribution exceeds the MT and AL ones
parametrically [167].
10.8.3 The Effect of Flu ctuations on the Hall
Conductivity
Let us start with a discussion of the physical meaning
of the Hall resistivity
xy
.In the case of only one type
of carriers it depends on their concentration n and
turns out to be independent of the electron diffusion
coefficient:
xy
= H/
(
en
)
. The fluctuation processes
of the MT and DOS types contribute to the diffusion
coefficient,so their expected contributionto the Hall
resistivity is zero.For the Hall conductivity in a weak
field one can write
xy
=
xy
2
xx
=
xy
(n)2
xx
+2
xy
(n)
xx
ı
xx
=
(n)
xy
1+2
ı
xx
xx
, (10.241)
so, evidently, the relative fluctuation correction to
Hall conductivity is twice as large as the fluctuation
correction to the diagonal component. This qualita-
tive speculation is confirmed by the direct calcula-
tion of the MT type diagram [168].
The AL process corresponds to an independent
charge transfer which cannot be reduced to a renor-
malization of the diffusion coefficient. It contributes
weakly to the Hall effect, and this contribution is
related to the Cooper pair particle-hole asymme-
try. This effect was investigated in a set of papers:
[69,168–173]. Let us recall that the proper general
expression describing the paraconductivity contri-
bution to the Hall conductivity in the general case
10 Fluctuation Phenomena in Superconductors 437
of arbitrary magnetic fields and frequencies (in the
TDGL theory limits) was already carried out above in
the phenomenological approach (see (10.131)). The
microscopic consideration of this value can be done
in the spirit of the calculation of
AL
xx
(see (10.200))
and after the analytical continuation results in
AL
xy
=
2h (0)
2
∞
n=0
(
n +1
)
/s
−/s
dk
z
2
∞
−∞
coth
z
2T
dz
×
Im L
R
n
(z)
@
@z
Re L
R
n+1
(z)
−ImL
R
n+1
(z)
@
@z
Re L
R
n
(z)
, (10.242)
where dimensionless magnetic field h was intro-
duced by (10.78). The phenomenological expression
(10.131) can be obtained from this formula by carry-
ing out the frequency integration in the same way as
was done in the calculation of (10.200) (the essential
region of integration is z T).
One can see from (10.242) that if Im L
R
n
(−z)=
−ImL
R
n
(z)andReL
R
n
(−z)=ReL
R
n
(z)theHallcon-
ductivity is equal to zero, or, in terms of the phe-
nomenological parametrization, the reality of
GL
results in a zero Hall effect. Physically it is possi-
ble to say that this zero is the direct consequence of
electron-hole symmetry. However, from the formula
(10.167) one can see that an energy dependence of
the density of states or the electron interaction con-
stant g immediately results in the appearance of an
imaginary part of
GL
. In the weak interaction ap-
proximation
Im
GL
=−
(0)
2
@ ln T
c
@E
E=E
F
. (10.243)
Usually this value is small in comparison with Re
GL
by a ratio of the order of T
c
/E
F
. Taking into account
the terms of the order of Im
GL
in (10.242) and us-
ing the explicit form of the fluctuation propagator
for layered superconductor (10.190) one can find
AL
xy
= (10.244)
e
2
T
Im
GL
2 (0)
h
×
/s
−/s
dk
z
2
1
+ r sin
2
(
k
z
s/2
)
2
×F
+ r sin
2
(
k
z
s/2
)
2h
%
,
where
F(x)=4x
2
(x)+x
(x)−1− (
1
2
+ x)
.
(10.245)
For H → 0 the expression for the fluctuation Hall
paraconductivity takes the form
AL
xy
=
e
2
T
6s
Im
GL
(0)
h
+ r/2
[
(
+ r
)]
3/2
. (10.246)
One can see that in the 2D case the temperature de-
pendenceoftheALfluctuationcorrectionontheHall
conductivity
AL
xy
≈
e
2
12s
T
c
E
F
h
2
turns out to be more singular than the MT one.
10.8.4 Fluctuations in the Ultra-Clean Case
When dealing with the superconductor electrody-
namics in the fluctuation regime, it is necessary to
remember that in the vicinity of the critical temper-
aturetheroleoftheeffectivesizeofafluctuation
Cooper pair is played by the GL coherence length
GL
(T)=
0
/
√
. So, as has already been mentioned
above,thecase of a pure enoughsuperconductor with
electron mean free path
0
has to be formally
subdivided into the clean (
0
GL
(T)) and
ultra-clean (
GL
(T) ) limits. The nontrivial can-
celation of the contributions, previously divergent in
T (see, for example, (10.206)), will be shown in this
section. This results in a reduction of the total fluc-
tuationcorrectionintheultra-cleancasetotheAL
term only. We will base our considerations on [174],
restricting our analysis to the case of a 2D electron
system.
438 A.I. Larkin and A.A.Varlamov
In terms of the parameter T,usedinthetheory
of disordered alloys, three different domains of the
metal purity can be distinguished: T 1(dirty
case),1 T 1/
√
(clean case),and 1/
√
T
(ultra-clean case of nonlocal electrodynamics). The
latter case has rarely been discussed in the litera-
ture [139,175,176]in spite of the fact that it becomes
of primary importance formetals of very modest pu-
rity, let us say, with T ≈ 10.Really,inthiscasethe
condition T ≥ 1/
√
, which in terms of the reduced
temperature is read as 10
−2
≤ 1,practically cov-
ers all the experimentally accessible range of tem-
peratures for the fluctuation conductivity measure-
ments. As regards the usually considered local clean
case(1 T 1/
√
) for the chosen value T ≈ 10,
it would not have any range of applicability. Indeed,
the equivalent condition for the allowed tempera-
ture interval is (T)
−2
anditalmostcontradicts
the 2D thermodynamical Ginzburg–Levanyuk crite-
rion for the mean field approximation applicability
(Gi
(2)
=
T
c
E
F
). Moreover, as we will show below,
for transport coefficients the higher order correc-
tionsbecome comparable with themean-field results
much before they are important for thermodynam-
ical quantities, namely at ∼
Gi
(2)
[177,178]. So
in practice one can speak about the dirty and the
nonlocal ultra-clean limits only.
As we saw abovethe 2D AL contribution turns out
to be completely independent of the electron mean
freepath [5].Theanomalous Maki–Thompsoncon-
tribution, beinginduced by the pairing on the Brow-
nian diffusive trajectories [76], naturally depends
on T, but in an indirect way. It turns out to be -
independent up to T ∼ 1/
√
(see (10.215)) and
diverges as T ln(T) for T 1/
√
[139, 175].
The analogous problem takes place in the case of
the DOS contribution: its standard diagrammatic
technique calculations lead to a negative correction
(10.206) [95], which is evidently strongly divergent
when T →∞. In the derivation of all these re-
sults the local form of the fluctuation propagator and
Cooperons were used. This is why the direct exten-
sion of their validity for T 1/
√
→∞is incor-
rect.
One can notice [174] that at the upper limit of
the clean case, when T ∼ 1/
√
,boththeDOSand
anomalous MT (10.215) contributions turn out to be
ofthesameorderofmagnitudebutofoppositesigns.
So one can suspect that in the case of a correct pro-
cedure of impurity averaging in the ultra-clean case
the large negative DOS contribution can be canceled
with the positive anomalous MT one. In the case of
a 2D electron spectrum the Cooperon can be cal-
culated exactly for the case of an arbitrary electron
mean free path:
(q, "
1
, "
2
)=
1−
Ÿ(−"
1
"
2
)
("
1
− "
2
)
2
+ v
2
F
q
2
%
−1
.
(10.247)
One can see that this expression can be reduced to
(10.184) in the case of v
F
q |"
1
− "
2
|. Let us stress
that this result was carried out without any expan-
sionovertheCooperpaircenterofmassmomentum
q and is valid in the 2D case for arbitrary q.
The fluctuation propagator in the 2D case of an
arbitrary mean free path can be written as [174]
−[ L(q, §
k
)]
−1
=ln
T
T
c
+
∞
n=0
1
n +1/2
(10.248)
−
1
n +
1
2
+
§
k
4T
+
1
4T
2
+
v
2
F
q
2
16
2
T
2
−
1
4T
.
Near T
c
ln
T
T
c
≈ and in the local limit, when
only small momenta q 1 are involved in
the final integrations, (10.248) can be expanded in
v
F
q/ max{T,
−1
} and reduces to the appropriate lo-
cal expression.
Let us demonstrate the specifics of the nonlocal
calculations for the example of the Maki–Thompson
contribution.We restrict our study to the vicinity of
the critical temperature, where the static approxima-
tion is valid. Using the nonlocal expressions for the
Cooperon and the propagator one can find after in-
tegration over electronic momentum:
Q
(MT )
(
!
)
=−4v
2
F
e
2
T
2
"
n
d
2
q
(2)
2
L(q, 0)
×
M
∼
n
,
∼
n+
, q
+ M
∼
n+
,
∼
n
, q
,
(10.249)
