Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

10 Fluctuation Phenomena in Superconductors 389
h r as an expansion over 1/,and it does not work
any more. Handling with the Hurvitz zeta-function
the summation in (10.81) for the 3D case can be car-
ried out for an arbitrary field [34]:
M
(3)
(; h r)=3
T
¥
0
s
2
r
1/2
√
h (10.82)
×
−
1
2
,
1
2
+
2h
−
1
2
,
1
2
+
2h
2h
.
One can see from this formula that for large fields
the magnetization saturates at the value M
∞
[49]:
M(h r) → M
∞
=−
ln 2
2
T
¥
0
s
=−0.346
T
¥
0
s
,
(10.83)
which is a typical for 2D superconductors. Therefore
at h ∼ r we have a 3D → 2D crossover in M(H)
behavior in spite of the fact that all sizes of fluctua-
tion Cooper pair considerably exceed the lattice pa-
rameters.The effective“bidimensionalization”of the
fluctuations is related to the effect of a strong mag-
netic field which “freezes out” the rotations along its
direction.Letusstressthatthiscrossoveroccursin
the region of already strongly nonlinear dependence
of M(H) and therefore for a rather strong magnetic
field from the experimental point of view in HTS.
Fixing the temperature r in the formula
(10.81) one can find the general formula for 2D fluc-
tuation regime [45]:
M
(2)
( r, h)=
T
¥
0
s
ln
1
2
+
2h
−
1
2
ln
(
2
)
(10.84)
−
2h
1
2
+
2h
−1
,
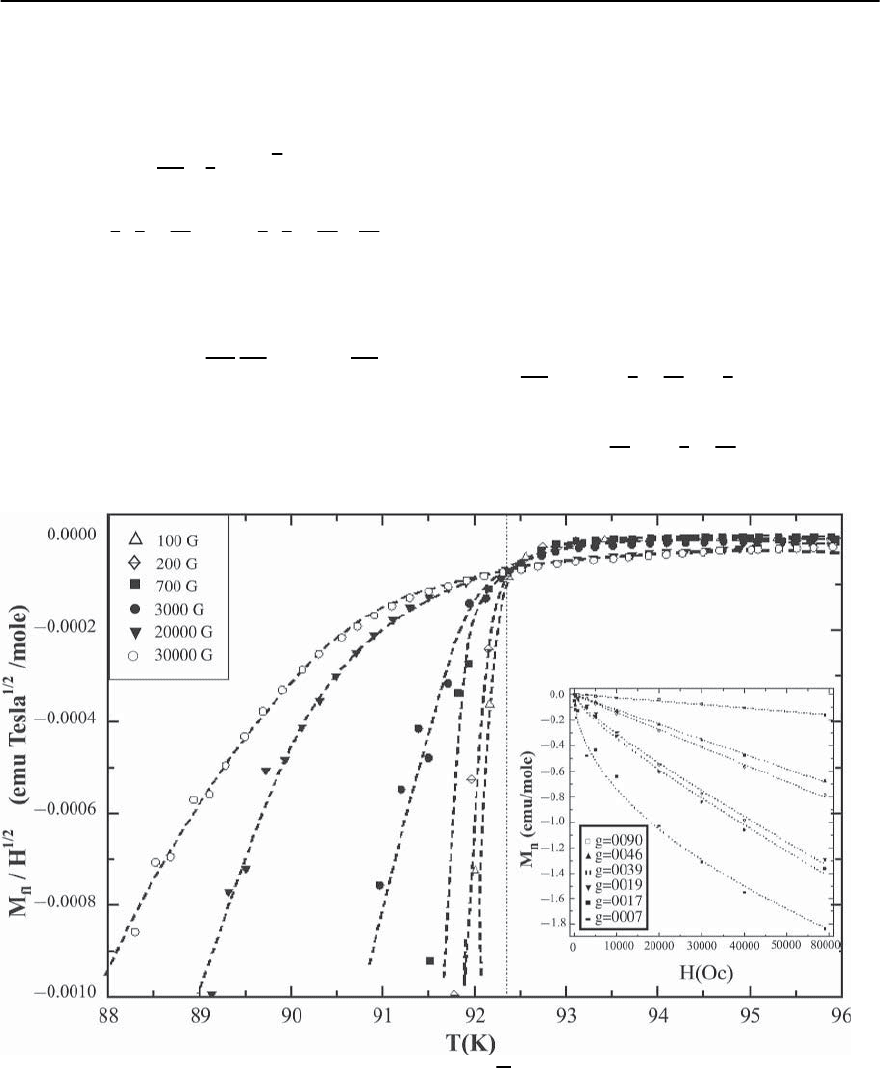
Fig. 10.4. Fluctuation magnetization of a YBCO123 normalized on
√
H as the function of temperature in accordance with
the described theory shows the crossing of the isofield curves at T = T
c
(0) = 92.3 K.The best is fit obtainedforanisotropy
parameter r =0.09. Inset: magnetization curves as the function of magnetic field
390 A.I. Larkin and A.A.Varlamov
where
(
x
)
is the Euler gamma-functionand
(
x
)
=
d ln (x)/dx was already cited in the introduction
digamma function. Using (10.84) one can directly
pass from the linear regime in a weak magnetic field
corresponding to (10.59) to the saturation of magne-
tization (10.83) in strong fields.
Near the line of the upper critical field (h
c2
()=
−)thecontributionofthetermwithn =0inthe
sum (10.81) becomes most important and for the
magnetization the expression
M(h) = −0346
T
¥
0
s
h
√
(h − h
c2
)(h − h
c2
+ r)
can be obtained.It contains the already familiar to us
“0D”regime(r h−h
c2
1),where the magnetiza-
tion decreases as −M(h) ∼
1
h−h
c2
(compare this with
(10.66)), while for h − h
c2
r the regime becomes
“1D” and the magnetization decreases more slowly,
as −M(h) ∼
1
√
h−h
c2
(see Fig. 10.3).
Such an analogy is observed in the next orders in
Gi too. In [50] the analogy was demonstrated for the
example of the first eleven terms for the 2D case and
nine for the 3D case. Summation of the series of high
order fluctuation contributions to the heat capacity
by the Pade–Borel method resulted in a temperature
dependence similar to the 0D and 1D cases without
the magnetic field. Nevertheless, a considerable dif-
ference should not be forgotten: in the 0D and 1D
cases no phase transition takes place, while in the
2D and 3D cases in a magnetic field a phase tran-
sition of first order to the Abrikosov vortex lattice
state occurs. In conclusion, the fluctuation magne-
tization of a layered superconductor in the vicinity
of the transition temperature turns out to be a com-
plicated function of temperature and magnetic field,
and it evidently cannot be factorized on these vari-
ables.Thefit of the experimental data is very sensitive
to the anisotropy parameter r and allows determina-
tion of the latter with a rather high precision [51,52].
In Fig.10.4 the successful application of the described
approach to fit the experimental data on YBa
2
Cu
3
O
7
is shown [53].
10.3 Fluctuations Below the Critical
Temperature
10.3.1 Effect of Fluctuations on Superfluid Density
and Critical Temperature
Superfluid Density
Among the important thermodynamical properties
of a superconductor is the magnetic field penetration
depth (T).Itis evidently asymmetric with respect to
the critical temperature, growing when the tempera-
ture tends to T
c
in the superconducting phase and is
infinite in the normal phase.The simple London elec-
trodynamics of a superconductor relates the current
density j and (T) to the superfluid density n
s
:
j =−n
s
2e
2
m
A =−
1
4
2
(T)
A,
2
(T)=
m
8n
s
e
2
.
(10.85)
GL theory permits calculating the temperature de-
pendence of (T) in the vicinity of the critical tem-
perature, identifying the superfluid density with the
average value of the order parameter
n
s
=
¦
2
=−
a
b
and, hence, predicting its inverse square root diver-
gence as a function of the reduced temperature:
(T)=
m
8e
2
b
˛T
c
||
. (10.86)
Let us study how the appearance of fluctuation
Cooper pairs affects the expulsion of the applied
magnetic field. The superfluid density goes to zero
at the transition point from below and its value de-
termines (T), so the effect of fluctuations may be
well pronounced.
Let us first convince ourselves that the presence
of fluctuation Cooper pairs above T
c
does not re-
sult in the appearance of a superfluid density. One
can calculate the fluctuation part of the supercur-
rent as ( [54,55] and a private communication from
A. Koshelev in 1999)

10 Fluctuation Phenomena in Superconductors 391
9
j
fl
:
=
−
@F
fl
(A)
@A
= T
@ ln Z(A)
@A
=−
D¦ (r)D¦
∗
(r)
@F [¦ (r),A]
@A
exp
−
F [¦ (r),A]
T
D¦ (r)D¦
∗
(r)exp
−
F [¦ (r),0]
T
.
This expression can be written in the form of two
contributions:
9
j
fl
:
= j
1
+j
2
=−
2e
2
m
A
9
|¦ (r)|
2
:
A=0
(10.87)
−
e
m
9
Im[¦ (r)∇¦
∗
(r)]
:
A
.
The first one, j
1
, just reproduces the London expres-
sion with the replacement of n
s
by
9
|¦ (r)|
2
:
.Inthe
average the GL free energy with A =0canbeused.
The second term, j
2
, has a more sophisticated na-
ture. To get it different from zero one has to include
the field dependent part of the GL free energy in
the process of further averaging in fluctuationfields.
Supposing the vector potential A to be weak enough
one can expand the Gibbs exponent in it and find
j
2
=−
e
2
m
2
T
'
Im[¦ (r)∇¦
∗
(r)] (10.88)
dV
1
Im[¦ (r
1
)∇¦
∗
(r
1
)]A(r
1
)
(
A=0
.
In the following we will restrict ourselves to a super-
conductor of the strongly second order ( 1). In
this case the characteristic scale of the space varia-
tion of A(r
1
) is much larger than that of the order
parameter, and the vector potential can be taken out
of the integral in (10.88).Thinking about the GL re-
gion above T
c
, one can expand the order parameter
in a Fourier series and reduce the averaging to the
expression
j
2
=
2e
2
m
k
k
A
@
@k
9
|¦
k
|
2
:
,
which yields
9
j
fl
:
= 0, as intuitively expected.
Below T
c
the situation is more cumbersome. In
order to calculate j
2
here let us separate the equilib-
rium value of the order parameter and its real and
imaginary fluctuating parts: ¦ (r)=
¦ +
r
+ i
i
.
This allows us to calculate the space integral in the
expression (10.88):
dV
1
Im[¦ (r
1
)∇¦
∗
(r
1
)] = 2i
k
k
rk
i,−k
.
The further functional integration can be carried out
in the spirit of the previous calculations for the fluc-
tuation contribution to the heat capacity below T
c
resulting in
9
j
fl
:
=−
2e
2
m
A
$
9
|¦ (r)|
2
:
A=0
−
k
T
(2˛T
c
|| + k
2
/4m)
&
.
Let us calculate the remaining
9
|¦ (r)|
2
:
=
¦
2
+
9
2
r
:
+
9
2
i
:
+2
¦
9
r
:
. The averaging of the first two terms
does not create any problem:
9
2
r
:
=
T
2
k
1
2˛T
c
|| + k
2
/4m
,
9
2
i
:
=
T
2
k
1
k
2
/4m
. (10.89)
In order to carry out the
9
r
:
term the anharmonic
contributionsin the GL functional, originatingfrom
the fourth order term, have to be taken into account:
9
r
:
=−
1
2
¦
3
9
2
r
:
+
9
2
i
:
. (10.90)
Finally one finds
9
j
fl
:
=−
2e
2
m
A
$
¦
2
−2
k
T
(2˛T
c
||+ k
2
/4m)
&
and the superfluid density takes the form
n
s
(T)=
˛
b
$
T
c
|| −
2b
˛
2
k
1
(2||+ k
2
/4m˛T
c
)
&
.
(10.91)
It is seen that in the 3D and 2D cases the sum over
momenta in (10.91) is formally divergent at large
k. This is not a first time when such problem has
arisen and we know how to deal with it: this ultra-
violet divergence is related to the restrictions on the
applicability of the GL functional for |k|
−1
,so
the integral has to be cut off at ·|k|= C ∼ 1.
392 A.I. Larkin and A.A.Varlamov
For the 3D case the transparent way to cut off the
sum is to separatethe upper and lower limit contribu-
tionsofthesum,which havedifferent physical senses,
by adding and subtracting the term ∼
|k|
−2
.Asa
result one obtains two contributions: the first one,
||-independent, originates from the upper limit cut
off and the second turns out to be proportional to
√
|| and appears from the lower limit. Using the
microscopic relations between the GL parameters
˛
2
/b =
8
2
7(3)
and 4m˛T
c
=
−2
one can finally find
n
s3
(T)=
32m
2
7(3)
T
c
2
(10.92)
×
2||T
c
−
7(3)
16
3
3
C
3
+
7(3)
16
2
3
2||
.
In the 2D case the problem of the ultra-violet diver-
gence is less important, since the cut off parameter
turns out to be involved in a logarithm:
n
s2
(T)=
32m
2
7(3)
T
c
2
T
c
||−
7(3)
16
3
2
ln
C
2
||
.
(10.93)
Fluctuation Shift of the Critical Temperature
Let us discuss the second term appeared in (10.93).
It evidently determines the fluctuation shift of the
critical temperature ıT
c
= T
c
− T
c0
,whereT
c0
is the
mean field (BCS) value of the transitiontemperature.
This shift
ıT
(3)
c
T
c0
∼ −
7(3)
16
3
T
c0
3
=−
8
Gi
(3)
coincides with that found in the framework of the
renormalization groupapproach(see(10.49)).In fur-
thercalculationswewillincludethis shiftin ||renor-
malizing the critical temperature to the value of T
c
and identifying it with the experimentally observed
transition temperature. The next order corrections
demonstrate that the substitutionof T
c0
→ T
c
is also
necessary in the last term of (10.93), so for the su-
perfluid density one can finally write
n
s3
(T)=n
BCS
s3
$
1+8
2Gi
(3)
||
&
.
In spite of the slower decrease of the fluctuation cor-
rection to the superfluid density when temperature
tends to the critical value, in comparison with the
main contribution (
√
|| instead of ||), it becomes
important only at ||∼Gi
(3)
.
The2Dsuperfluid density (10.93) canbealsowrit-
ten in terms of the 2D Ginzburg–Levanyuk number:
n
s2
(T)=
mT
c
Gi
(2)
|| −2Gi
(2)
ln
C
2
||
(10.94)
and finally expressed in terms of the fluctuations
renormalized criticaltemperature.It is enough to in-
clude the cut off parameter in the T
c
-shift (compare
with the RG estimation (10.47)):
ıT
(2)
c
T
c0
=−2Gi
(2)
ln
C
2
Gi
(2)
,
which results in
16
n
s2
(T)=n
BCS
s2
1−2
Gi
(2)
||
ln
Gi
(2)
||
. (10.95)
10.3.2 Phase Fluctuations in 2D Systems
Let us discuss the results obtained for the superfluid
density in the 2D systems. Being in the limits of the
GL theory we cannot enter into the critical region,
so the result (10.95) is valid for ||Gi
(2)
only.
At the same time the Berezinski–Kosterlitz–Thouless
(BKT) theory of critical fluctuations in 2D systems
establishes the value of superfluid density at the crit-
ical temperature (Nelson–Kosterlitz jump [56]) as:
n
s2
(T
c
)=
4mT
c
. (10.96)
An interpolation formula for the superfluid density
of the 2D system can be written [13] by the unifica-
tion of (10.95) and (10.96):
n
s2
(T)=
mT
c
||
Gi
(2)
−2ln
Gi
(2)
||+ Gi
(2)
+4
.
16
For sake of simplicity we still call the reduced temperature
T
c
−T
T
c
as .
10 Fluctuation Phenomena in Superconductors 393
One can notice that the fluctuation correction to
the average value of order parameter
9
:
=
9
r
:
below
T
c
is divergent (see (10.89)). This means that the ap-
propriate correctionscannot be supposed to be weak
even relatively far from the transition ||Gi
(2)
,
where the fluctuations of the value
9
|¦ (r)|
2
:
are still
small. Neglecting the order parameter modulus fluc-
tuations one can write the effective functionalwhich
describes the order parameter phase fluctuations
only:
F[']=
n
s
4m
d
2
r
∇'
2
=
n
s
4m
k
k
2
'
2
k
.
Let us calculate now the average value of the order
parameter using this functional without the assump-
tion of weak fluctuations:
¦ = |¦ |
9
e
i'
:
= |¦ |
/
exp
−
k
4mT
n
s
k
2
%0
.
(10.97)
In the 2D case the sum in (10.97) diverges and
¦ = 0 [57]. Nevertheless a phase transition in such
system exists. In order to see this let us study the
behavior of the correlation function ¦
∗
(0)¦ (r) at
large distances.
Above the mean field critical temperature the
Fourier component |¦
k
|
2
can be easily calculated
with the use of expression (10.27):
|¦
k
|
2
=
D¦
k
D¦
∗
k
|¦
k
|
2
exp
=
−˛( +
2
k
2
)|¦
k
|
2
>
D¦
k
D¦
∗
k
exp
=
−˛( +
2
k
2
)|¦
k
|
2
>
=
1
˛( +
2
k
2
)
, (10.98)
and the correlator ¦
∗
(0)¦ (r) takes the form:
9
¦
∗
(0)¦ (r)
:
(TT
c0
)=
k
9
|¦
k
|
2
:
exp
(
ikr
)
=
1
4˛
2
K
0
r
()
, (10.99)
where K
0
(x) is the modified Bessel function.At large
arguments K
0
(x 1) =
2x
e
−x
and we find that in
the normal phase this correlator decreases exponen-
tially at distances r ().
Below the transition point it is
9
¦
∗
(0)¦ (r)
:
= |¦ |
2
9
exp
i' (0) − i'(r)
:
= |¦ |
2
/
exp
i
k
1−exp
(
ikr
)
'
k
%0
(10.100)
= |¦ |
2
exp
−
1
2
k
|1−exp
(
ikr
)
|
2
9
'
2
k
:
%
.
The average value
9
'
2
k
:
has already appeared in our
calculations (for instance, in (10.89)) as the phase
fluctuationmodebelowT
c
:
9
'
2
k
:
=4mT
n
s
k
2
−1
.The
last integral (sum) in the exponent of (10.100) evi-
dently converges at small k. After the angular inte-
gration it can be expressed in terms of an integral
of a Bessel function and it logarithmically diverges
at the upper limit. This divergence must be cut off
at k ∼
−1
, where the expression for
9
'
2
k
:
is no longer
valid. As a result below the transition point the cor-
relator takes the form
9
¦
∗
(0)¦ (r)
:
|r|
(T < T
c0
) (10.101)
= |¦ |
2
exp
−
mT
n
s
ln
r
= |¦ |
2
r
−
mT
n
s
.
These two (10.99) and (10.101), quite different,
asymptotics of the correlator for the low and high
temperaturelimitswereobtainedfortheregions
|| Gi
(2)
. Nevertheless it is clear that there must
be some point at which the high temperature expo-
nential asymptotic changes to the low temperature
power one. This temperature is reasonably called the
point of the superconducting transition. In the 2D
case such a transition is called the BKT transition.We
do not discuss its properties in this review (see, for
instance,the review articles of P.Minnhagen [58,59]).
It is worth mentioningthat,in spite of the fluctuation
destruction of
9
:
, in the low temperature phase the
observable physical quantity n
s
is renormalized by
fluctuations finitely and is not zero. In the GL region
(|| Gi
(2)
) this renormalization even turns out to
be weak.
10.3.3 Phase-Slip Events in 1D Systems
In the case of a 1D wire (10.91) also gives a small
correction to n
s
. At the same time it is clear that at
T = 0 the phenomenon of the superconductivity in

394 A.I. Larkin and A.A.Varlamov
1D does not exist. This results from: (a) the general
statement about the absence of the phase transitions
in 1D systems; (b) the evident exponential decrease
of the correlator (10.100) for a 1D system below the
transition point; and (c) the partition function in 1D
can be calculated exactly.
17
So, if the phase fluctuations are unable to destroy
n
s
, what is the mechanism for killing superconduc-
tivity in 1D systems? It turns out that it is phase-
slip events, which can also be called instantons or
topological excitations. At temperatures beyond the
critical region (|| Gi
(2)
) the probability of such
excitations is exponentially small and they cannot be
found by the methods of perturbation theory.
There is a general statement of the absence of
phase transitions in one-dimensional systems. The
superconductive phase should be unstable and su-
percurrents cannot persist for a long time and must
decay. Phase-slips are the mechanism of the super-
current decay. Let us consider a closed loop made
from a one-dimensional superconducting wire. The
magnetic flux through this loop is a constant. If the
phase of the wave function is a continuous func-
tion of the position, then it is not possible to change
the supercurrent in the loop gradually. However, due
to fluctuations, there is a finite probability to have
the modulus of the order parameter vanish at some
point.Thus,the phase is not defined at this point and
a phase-slip may occur (a change of the phase along
the loop by 2). Thus, the supercurrent that is de-
termined by the gradient of the phase decays. Let us
note that this reasoning works for one-dimensional
systems only. In higher-dimensional systems, it is al-
ways possible to connect any two points by a path
along which the phase is a continuous function.
With the aim of understanding the origin of
phase-slip events let us start from a discussion of
a small Josephson junction included in a supercon-
ducting ring of induction L. The potential energy
related with the phase difference at the junction is
the same as in a layered superconductor (10.69), so
the energy of the ring can be expressed in terms of
the magnetic flux ¥
18
E
r
= E
J
cos
2¥
¥
0
+
¥
2
2L
. (10.102)
Besides the ground state with ¥ =0therearemany
metastable states with ¥ near n¥
0
in such a system.
The energies of such states are also the minima of
the expression (10.102), but not absolute minima.
In the limit of large E
J
the energies of these min-
ima are equal to ¥
2
0
n
2
/2L.Inordertotransitfrom
one metastable state to another one with lower en-
ergy, the system has to pass through a potential bar-
rier.The heights of these barriers are determined by
the maxima of Ex.(10.102) and are equal to 2E
J
.The
probability of such a “jump” (so-called “phase-slip
process”) is proportional to exp{−2E
J
/T}.Theflux
flow decay, and respectively, the voltage in the circuit
are proportional to this probability:
U =
d¥
dt
∼ exp{−2E
J
/T}.
The positions of the maxima and minima of the
function (10.102) are determined by the condition
@E
r
/@¥ = 0. Let us consider the mechanism of the
phase slip process in the circuit when the super-
conducting wire does not have a weak link and its
free energy can be described by the GL functional
(10.16). The minima of this expression are equal
17
It is possible to demonstrate [60] that the free energy of a D-dimensional classical field is equal to the ground state
energy of the related D − 1-dimensional quantum mechanical system. Indeed, in the 1D case the functional integral
turns out to be the same as the Feynman integral for a particle moving in the potential a|¦ |
2
+
b
2
|¦ |
4
.Thegroundstate
energy in this case is an analytical function of a and does not have a singularity at any temperature.
18
The Josephson part of the Ginzburg–Landau energy, related to interlayer tunneling, was written as J |¦
n
− ¦
n−1
|
2
(see
(10.69)). Supposing ¦
n
= |¦ |e
i' n
one can rewrite the corresponding energy as 2J |¦ |
2
(1 − cos ').Applying this result
to the superconducting ring with a weak link one can express the phase difference by means of the magnetic field flux:
' =
∇'dl =2e
Adl =2¥/¥
0
.

10 Fluctuation Phenomena in Superconductors 395
to −a
2
U/2L+ ¥
2
0
n
2
/2L and they correspond to the
magnetic flux quantum ¥
0
. The transition between
the neighboring minima can only occur through the
saddle points of the functional (10.16).These saddle
points correspond to the unstable solutionsof the GL
equation
¦ +
b
a
¦
3
+
2
(T)¦
=0.
The solutions of this equation are continuous in the
same way as those corresponding to the minima of
the functional, but they can pass through zero at
some points where the modulus of the order parame-
ter is equal to zero [61].In the vicinity of these points
the solution of the GL equation takes the form of an
instanton:
¦ (x)=
7
−
a
b
th
x
2(T)
.
Substituting it into (10.16) one can find the energy
of such an instanton in the wire of the cross-section
S is [62]:
F
0
=
8
√
2
3
a
2
2b
S(T)=
√
2
3
||
Gi
(wire)
3/2
T .
So the probability for the superconducting ring to
change its magnetic flux by one flux quantum only
implies that, being thermically activated, it passes
over such a barrier. It turns out to be exponen-
tially small, and the wire resistance is equal to R ∼
exp{−F
0
/T}.
In the case of a thin film the topological defects
carrying the flux quantaare given by fluctuationvor-
tices. The energy of such a vortex is equal to
E =
n
s
4m
ln
.
In a thin film is very large.In the framework of the
BKT theory it is assumed to be infinite. Thusthe film
resistivity below the critical temperature turns out to
be zero.
10.3.4 Fluctuations of Magnetic Field
In the above consideration we discussed fluctuations
of the order parameter only supposing the magnetic
field to be a constant. At the same time the natural
question arises: what is the effect of the usual black-
body radiation fluctuations on the superconductor
properties? From the very beginning one can expect
this effect to be small at low temperature. The or-
der parameter fluctuation effects in bulk materials
also turned out to be negligible. In the case of type I
superconductors the coherence length can notice-
ably exceed the magnetic field penetration depth .
This means that the magnetic field fluctuations will
take place on a scale less than the characteristic su-
perconducting one,which can change some intrinsic
superconducting properties. In this section we will
show that magnetic field fluctuations, being small in
amplitude, can change the order of phase transition
of a type I superconductor.
The same GL functional formalism permits us
to take into account the fluctuations of a magnetic
field [63]. Let us suppose that the external magnetic
field H = 0, the system is below the critical temper-
ature, the value of the equilibrium order parameter
is
¦ , and we neglect its fluctuations.Further calcula-
tions can be done in the spirit of the order parame-
ter fluctuation calculations. One can rewrite (10.64)
as the functional of the fluctuating vector potential,
choosing the gauge · A = 0 and writing it in the
form of Fourier series:
F[A(r)] = F
N
+
dV
×
a|
¦ |
2
+
b
2
|
¦ |
4
+
e
2
|
¦ |
2
m
A
2
+
k
2
A
2
8
= F
s
[
¦ , 0] +
k
e
2
|
¦ |
2
m
+
k
2
8
A
2
k
.
The corresponding free energy can be written as
F = F
s
[
¦ , 0] + ln
DA
x
DA
y
× exp
−
1
T
k
e
2
|
¦ |
2
m
+
k
2
8
A
2
k
%
= F
s
[
¦ , 0] + T
k
ln
T
e
2
|
¦ |
2
m
+
k
2
8
. (10.103)
In the 3D case the sum in (10.103) evidently strongly
diverges. The most divergent term is nothing else
396 A.I. Larkin and A.A.Varlamov
than the consequence of the ultra-violet catastrophe
and,as usual, it can simply be attributed to the back-
ground value of the free energy. The next, propor-
tional to |
¦ |
2
, contribution to the sum in (10.103)
also turns out to be divergent. This divergence we
treat in the same way as above: renormalize the crit-
ical temperature of the superconducting transition
with respect to its mean field value. Regularized in
this way free energy can finally be rewritten as
F = F
N
+ a|
¦ |
2
−
16T
√
e
3
m
3/2
|
¦ |
3
+
b
2
|
¦ |
4
.
One can see that an unusual cubic term appears
in it due to the fluctuations of the electromagnetic
field. This contribution, even being small in magni-
tude,changestheorder of thesuperconducting phase
transition.Indeed,putting a = 0 one can see that the
minimum of the free energy takes place for a posi-
tive order parameter value. This means that already
for positive a thefreeenergyhastwominima(one
at ¦ = 0 and a second for positive ¦ )appropriate
to the normal and superconducting states.A first or-
der phase transition takes place when the values of
the free energy in both of these minima coincide,
i.e. ata = 128T
2
e
6
/bm
3
, or, using the microscopic
expressions for and ˛
2
/b,at
=
˛
2
b
2
13
T
4
e
6
(
4˛mT
)
3
=2·
(
2
)
4
Gi
(3)
(T)
(T)
6
.
From this result one can see that for a type I super-
conductor this region noticeably exceeds the critical
one and the phase transition,dueto electromagnetic
field fluctuations, turns out to be of first order.
For type II superconductors the region of temper-
atures
, where the electromagnetic field fluctuations
are important, turns out to be inside the critical one.
This means that these fluctuations have to be taken
into account in the equations of the renormalization
group, which also results in the conclusion of a first
order phase transition in type II superconductors.
Nevertheless for temperatures Gi
(3)
these effects
are negligible and in the following discussion we will
not take them into account.
10.4 Ginzburg–Landau Theory
of Fluctuations in Transport
Phenomena
The appearance of fluctuating Cooper pairs above T
c
leads to the opening of a “new channel” for charge
transfer. In the Introduction the fluctuation Cooper
pairs were treated as carriers with charge 2e while
their lifetime
GL
was chosen to play the role of the
scattering time in the Drude formula. Such a quali-
tative consideration results in theAslamazov–Larkin
(AL) pair contribution to conductivity (10.11) (so-
called paraconductivity.
19
)
Below we will present the generalization of the
phenomenological GL functional approach to trans-
port phenomena. Dealing with the fluctuation or-
der parameter, it is possible to describe correctly
the paraconductivity type fluctuation contributions
to the normal resistance and magnetoconductiv-
ity, the Hall effect, thermoelectric power and ther-
mal conductivity at the edge of transition. Unfor-
tunately the indirect fluctuation contributions are
beyond the possibilities of the description by the
time-dependent GL approach and they will be cal-
culated in the framework of the microscopic theory
(see Sects. 10.6–10.8).
10.4.1 Time-Dependent GL Equation
In previous sections we demonstrated how the GL
functional formalism allows one to account for fluc-
tuation corrections to thermodynamical quantities.
Let us discuss the effect of fluctuations on the trans-
port properties of a superconductor above the criti-
cal temperature.
In order to find the value of paraconductivity,
some time-dependent generalization of the GL equa-
tions is required.Indeed,the conductivity character-
izes the response of the system to the applied electric
field. It can be defined as E =−@A/@t but, in con-
trast to the previous section, A has to be regarded
19
This term may have different origins.First of all,evidently,paraconductivity is analogous to paramagnetism and means
excess conductivity.Another possible origin is an incorrect onomatopoeic translation from the Russian“paroprovodi-
most”, which means pair conductivity.

10 Fluctuation Phenomena in Superconductors 397
as time-dependent. The general nonstationary BCS
equations are very complicated, even in the limit of
slow timeandspace variationsof thefield and the or-
der parameter. For our purposes it will be sufficient,
following [64–70], to write a model equation in the
vicinity of T
c
, which in general correctly reflects the
qualitative aspects of the order parameter dynamics
and in some cases is exact.
Let us keep in mind the GL functional formalism
introduced above. If a deviation from equilibrium is
assumed, then it is no longer possible to derive the
GL equations starting from the condition that the
variational derivative of the free energy is zero. At
the same time, in the absence of equilibrium ¦ be-
gins to depend on time.For small deviations from the
equilibrium it is natural to assume that in the pro-
cess of order parameter relaxation its time derivative
@¦ /@t is proportional to the variational derivative of
the free energy ıF/ı¦
∗
, which is equal to zero at
the equilibrium.But this is not all: side by side with
the normal relaxation of the order parameter the ef-
fect of thermodynamical fluctuations on it has to be
taken into account. This can be done by the intro-
duction the Langevin forces (r, t)intherighthand
side of equation describing the order parameter dy-
namics.Finally,gauge invariance requires that @¦ /@t
should be included in the equation in the combina-
tion @¦ /@t +2ie'¦,where' is the scalar potential
of the electric field. By concluding all these specu-
lations one can write the model time-dependent GL
equation (TDGL) in the form
−
GL
@
@t
+2ie'
¦ =
ıF
ı¦
∗
+ (r, t) . (10.104)
with the GL functional F determined by (10.16),
(10.64), and (10.69). The dimensionless coefficient
GL
in the left hand-sideof theequationcan berelated
to pair lifetime
GL
(10.2):
GL
= ˛T
c
GL
= ˛/8by
the substitution in (10.104) ofthefirst termof (10.16)
only.
20
Neglecting the fourth order term in the GL func-
tional, (10.104) can be rewritten in operator form
as
[
B
L
−1
−2ie
GL
'(r, t)]¦ (r, t)=(r, t) , (10.105)
with the TDGL operator
B
L and Hamiltonian
C
H de-
fined as
B
L =
GL
@
@t
+
B
H
−1
, (10.106)
C
H = ˛T
c
−
B
2
(
B
∇ −2ieA)
2
.
We have introduced here the formal operator of the
coherence length
B
to have the possibility to deal
with an arbitrary type of spectrum. For example, in
the most interesting case for our applications to lay-
ered superconductors, the action of this operator is
defined by (10.69).
In the absence of an electric field one can write
the formal solution of (10.105) as
¦
(0)
(r, t)=
B
L(r, t) . (10.107)
The Langevin forces introduced above must satisfy
the fluctuation-dissipation theorem, which means
that the correlator ¦
(0)∗
p
(t
)¦
(0)
p
(t) at coinciding
momentsoftimehastobethesameas|¦
p
|
2
,
obtained by averaging over fluctuations in thermal
equilibrium (see (10.98)). This requirement is ful-
filled if the Langevin forces (r, t)and
∗
(r, t)are
correlated by the Gaussian white-noise law
∗
(r, t)(r
, t
) =2T Re
GL
ı(r − r
)ı(t − t
) .
(10.108)
To show itlet us restrict ourselves for sake of simplic-
ity to the case of A = 0 and calculate the correlator
¦
∗
(r, t)¦ (r
, t) =
∗
(r, t)
B
L
∗
B
L(r
, t)
=2T Re
GL
dp
(2)
D
e
ip(r−r
)
(10.109)
×
∞
−∞
d§
2
L
∗
(p, §)L(p, §) .
L(p, §) can be found by performing the Fourier
transform in (10.107):
L(p, §)=(−i
GL
§ + "
p
)
−1
, (10.110)
20
It will be shown below that taking into account the electron–hole asymmetry leads to the appearance of an imaginary
part of
GL
proportional to the derivative @ ln(v
2
)/@E|
E
F
∼ O(1/E
F
). This is important for such phenomena as the
fluctuation Hall effect or fluctuation thermopower and, having in mind the most general formula, we will suppose
GL
= ˛/8+i Im
GL
, where necessary.

398 A.I. Larkin and A.A.Varlamov
resulting in
9
¦
∗
(r, t)¦ (r
, t)
:
p
=2T Re
GL
(10.111)
∞
−∞
d§
2
1
2
GL
§
2
+ "
2
p
=
9
|¦
p
|
2
:
,
where
"
p
= ˛T
c
( +
B
2
p
2
) . (10.112)
is the Cooper pair energy spectrum.
10.4.2 Paraconductivity
Letus try to clear up the reason why the simple Drude
formula works so well for complex phenomenon like
paraconductivity.Forthispurpose let ustry to derive
the Boltzmann master equation for the fluctuation
Cooper pair distribution function
n
p
(t)=
9
¦ (r, t)¦
∗
(r
, t)
:
(10.113)
× exp(−ip(r − r
))d(r − r
) .
Let us recall that in the state of thermal equilibrium
n
(0)
p
= |¦
p
|
2
= T/"
p
.
In order to determine the electric field dependence
of n
p
let us write its time derivative using (10.104)
@n
p
(t)
@t
=
d(r − r
)e
−ip(r−r
)
×
'
@¦ (r, t)
@t
¦
∗
(r
, t)
(
+
'
¦ (r
, t)
@¦
∗
(r, t)
@t
(
=
d(r − r
)e
−ip(r−r
)
2
e
i
['(r)−'(r
)]¦ (r, t)¦
∗
(r
, t) .
+
2
GL
Re
'
¦ (r, t)
ıF
ı¦
(r
, t)
(
+
2
GL
Re
9
(r, t)¦
∗
(r
, t)
:
,
(10.114)
where F is determined by (10.64). Expressing the
scalar potential by the electric field E one can trans-
form the first term of the last integral into −2eE
@n
p
@p
.
The term with the variational derivative can be eval-
uated by means of (10.27) and expressed in the form
−
2
GL
"
p
n
p
. The evaluation of the last term is more
cumbersome because it contains the Langevin force.
To the first approximation it is possible to use here
the order parameter ¦
(0)
(r, t) (see (10.107)) un-
perturbed by the electric field as the convolution
B
L(r, t). In this way, using (10.108) and (10.109) we
calculate the last average in (10.114)
2
GL
d(r − r
)e
−ip(r−r
)
Re
9
∗
(r, t)
B
L(r, t)
:
=2T Re
∞
−∞
d§
2
L(p, §)=
2T
GL
=
2
GL
"
p
n
(0)
p
and obtain the transport equation
@n
p
@t
+2eE
@n
p
@p
=−
2
GL
"
p
n
p
− n
(0)
p
=−
2
p
n
p
− n
(0)
p
. (10.115)
In the absence of a magnetic field "
p
is determined
by (10.112) and the momentum-dependent lifetime,
corresponding to the Ginzburg–Landau one, can be
introduced:
p
=
GL
/"
p
=
GL
()
1+
2
()p
2
.
Letusstresstheappearanceofthecoefficient2onthe
right hand side of the equation (10.115). This means
that the real Cooper pair lifetime, characterizing its
density decay, is
p
/2.
The effect of a weak electric field on the fluctua-
tion Cooper pair distribution function in the linear
approximation is determined by
n
(1)
p
=−
eE
GL
"
p
@n
(0)
p
@p
=
eT
GL
"
3
p
E ·
@"
p
@p
. (10.116)
Substituting this formula into the expression for the
electric current (10.88) side by side with the Cooper
pair velocity v
p
= @"
p
/@p one can find
j
˛
=
p
2ev
˛
n
p
=
˛ˇ
E
ˇ
,
where the paraconductivity tensor components are:
˛ˇ
(D)
=
4
e
2
˛T
p
v
˛
p
v
ˇ
p
"
3
p
. (10.117)
In the case of an isotropic spectrum
