Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

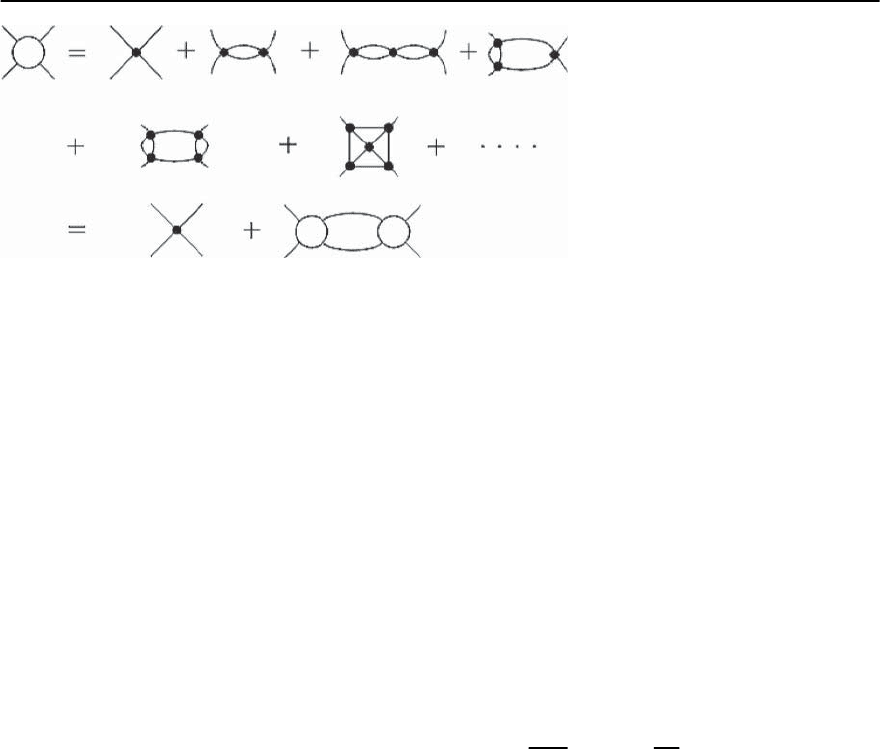
10 Fluctuation Phenomena in Superconductors 379
Fig. 10.2. Examples of diagrams for the
fluctuation contribution to b
is sufficient to sum the relatively simple “parquet”
type diagrammatic series. Such a summation results
in the substitution of the “bare” vertex b by some
effective interaction
b, which diminishes and tends
to zero when the temperature approaches the tran-
sition point. Such a method was originally worked
out in quantum field theory [15–17]. For the prob-
lem of a phase transition such a summation was first
accomplished in [18].
Instead of a direct summation of the diagrams it
is more convenient and physically obvious to use the
method of the renormalization group. In the case
of quantum field theory this method was known
long ago [19,20]. For phase transition theory it was
proposed in [18,21], but the most simple and evi-
dent formulation was presented by Wilson [22]. The
idea of the renormalization group method consists
in separating the functional integration over “fast”
(
|k|
)and“slow”(
|k|<
)fluctuationmodes.Ifthe
cut off is large enough the fast mode contribution
is small and the integration over them is Gaussian.
After the first integration over fast modes the func-
tional obtained depends on the slow ones only. They
can, in turn, be divided into slow (|k| <
1
)andfast
(
1
< |k| < ), and the procedure can be repeated.
Moving step by step ahead in this way one can calcu-
late the complete partition function.
As an example of the first step of renormalization,
the partition functioncalculationbelow T
c
can be re-
called. There we separated the order parameter into
the space-independent part
¦ (“slow”mode) and the
fluctuation part (r) (“fast” mode), which was be-
lieved to be small in magnitude. Being in the GL re-
gion it was enough to average over the fast variables
just once,while in the critical region therenormaliza-
tion procedure requires subsequent approximations.
The cornerstone of the method consists in the fact
that in the critical region at any subsequent step the
free energy functional has the same form.ForD close
to 4 this form coincides with the initial free energy
GL functional butwith the coefficientsa
and b
de-
pending on .We will perform these calculations by
the method of mathematical induction. Let us sup-
pose that after the (n − 1)-st step the free energy
functional has the form:
F [
¦
n−1
]=F
N,
n−1
+
dV
a
n−1
|
¦
n−1
|
2
+
b
n−1
2
|
¦
n−1
|
4
+
1
4m
|∇
¦
n−1
|
2
. (10.40)
Writing
¦
n−1
in the form
¦
n−1
=
¦
n
+
n
and
choosing
n
close enough to
n−1
it is possible to
make
n
so small that one can restrict the func-
tional to the quadratic terms in
n
only and per-
form the Gaussian integration in complete analogy
with (10.34). The important property of the spaces
with dimensionalities close to 4 is the possibility to
choose
n
n−1
and still to have
n
¦
n
.In
this case
¦
n
canbetakenasanindependentcoor-
dinate, and one can use the result directly following
from (10.34):
380 A.I. Larkin and A.A.Varlamov
F [
¦
n
]=F
N,
n−1
+
dV
a
n
|
¦
n
|
2
+
b
n
2
|
¦
n
|
4
+
1
4m
|∇
¦
n
|
2
−
T
2
n
|k|
n−1
1
ln
T
c
(3b
n
|
¦
n
|
2
+ a
n
+
k
2
4m
)
+ln
T
c
b
n
|
¦
n
|
2
+ a
n
+
k
2
4m
2
.(10.41)
Expanding the last term in (10.41) in a series in
¦
n
one can get for F[
¦
n
] the same expression (10.40)
with the substitution of
n−1
→
n
. From (10.41) it
follows that
F
n,
n
= F
n,
n−1
− T
n
|k|
n−1
ln
T
c
a
n
+
k
2
4m
,
a
n
= a
n−1
+2T
n
|k|
n−1
b
n
a
n
+
k
2
4m
, (10.42)
b
n
= b
n−1
−5T
n
|k|
n−1
b
2
n
a
n
+
k
2
4m
2
.
Passing to a continuous variable
n
→ one can
rewrite these recursion equations as the set of differ-
ential equations:
@F()
@
=−T
D
D−1
ln
T
c
a()+
2
4m
, (10.43)
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎩
@a()
@
=−2T
D
b()
D−1
a()+
2
4m
@b()
@
=5T
D
b
2
()
D−1
a()+
2
4m
2
. (10.44)
These renormalization group equationsareevidently
valid for small enough only, where the transition
from discrete tocontinuousvariablesisjustified.This
means at least
2
/4m T
c0
Gi
(D)
(10.45)
in order to move away from the first approximation.
Let us recall that in the framework of the Landau
theory of phase transitions the coefficienta(T
c0
)=0
at the transition point and this can be considered as
the MFA definition of the critical temperature T
c0
.
The same statement for the function a = a()in
the framework of the renormalization group method
canbewrittenasthea(T
c0
, ∼
−1
) = 0. With the
decrease of the effect of critical fluctuations is in-
creasingly taken into account and the renormalized
value of the critical temperature decreases, being de-
fined by the equation: a(T
c
(), ) = 0. Finally, after
the application of the complete renormalization pro-
cedure, one can define the real critical temperature
T
c
, shifted down with respect to T
c0
due to the effect
of fluctuations, from the equation:
a(T
c
, =0)=0. (10.46)
It is easy to find this shift in the first approximation.
Indeed, let us integrate the first equation of (10.44)
over in limits [0,
−1
]. The main contribution to
the integral will be determined by the region where
a()
2
4m
.Being far from the criticalpoint one can
assume that the coefficient b =const. and then
a(
−1
)=˛ıT
c
=
a(
−1
)
a(0)
da =−8mT
D
b
1/
0
D−3
d .
For the 3D case this gives the shift of the criticaltem-
perature ıT
c
due to fluctuations
11
11
In the same way we can also analyze the shift of the critical temperature in the 2D case and obtain:
ıT
(2)
c
T
c
=−2Gi
(2)
ln
1
4Gi
(2)
. (10.47)
As we will show below both 3D and 2D results for ıT
c
coincide with those obtained by the analysis of the effect of
fluctuations on superconducting density in the perturbation approach.
10 Fluctuation Phenomena in Superconductors 381
ıT
(3)
c
T
c
∼ −
2mb
˛
=−
b
2T
c
˛
2
1
3
(10.48)
=−
7(3)
16
3
T
c
3
=−
8
Gi
(3)
.
Let us comeback to study of properties of the system
of equations (10.44).Onecan find its partial solution
at T = T
c
in the form:
a(T
c
, )=
4−D
4m[5 + (4 − D)]
2
, (10.49)
b(T
c
, )=
5
16m
2
T
D
4−D
[5 + (4 − D)]
2
4−D
.
These power solutions are correct in the domain of
validity of the system (10.44) itself, i.e. for small
enough defined by the condition (10.45). Nev-
ertheless, in a space of dimensionality close to 4
(D =4−", " 1) it is possible to extend their valid-
ity up to the GL region and to observe their crossover
to the GL results: a(T
c
)=0;b(T
c
)=b
0
=const. In-
deed, in this case, due to proportionality of a()to
" → 0, one can omit it in the denominators of the
system (10.44) and to write down the solution for
b() in the form
b
−1
(T
c
, )=b
−1
0
+
80m
2
(4 − D)
T
D
(
D−4
−
4−D
) .
(10.50)
We have chosen the constant of integration as b
−1
0
−
80m
2
(4−D)
T
D
4−D
in order to match the renormaliza-
tion group and GL solutions at the value of =
max
∼
−1
. Now let us pass to study of the func-
tion a(T, ) for the same interesting case of space
dimensionality D → 4 for temperatures slightly dif-
ferent (but still close enough) from T
c
, where one
can write
a(T, )=a(T
c
, )+˛(T
c
, )T
c
.
The firsttermonthe righthand sideisdetermined by
(10.49).In order to determine ˛(T
c
, ) let us expand
the first equation in (10.44) in terms of
@˛(T
c
, )
@
=2T
D
b(T
c
, )
D−1
a(T
c
, )+
2
4m
2
˛(T
c
, ) .
(10.51)
For
2
/4m ˛(T
c
, )T
c
(10.52)
we can again use the solution (10.50) for b(T
c
, )
and omit a(T
c
, ) in the denominator of (10.51).
The constant of integration,appearing in the process
of solution of (10.51) is chosen in accordance with
the condition that for =
max
∼
−1
we match
˛(T
c
, )=˛(T
c0
,
−1
)=˛
0
with the GL theory:
˛(T
c
, )=˛
0
1+
80m
2
b
0
(4 − D)
T
D
(
D−4
−
4−D
)
−2/5
.
(10.53)
The condition (10.52) can be written as
−1
(T),
where (T) is the generalized coherence length, de-
termined by the equation:
−2
(T)=4m˛
T
c
,
−1
(T)
T
c
.
Such a definition is valid at any temperature. For
example, far enough from the critical point, in the
GL region, ˛
T
c
,
−1
(T)
= ˛
0
and one reproduces
the result (10.3). Vice versa, in the critical region
the main contribution on the right hand side of the
(10.53)results from the second term containing
D−4
so, putting
−1
(T)=, one can rewrite the self-
consistent equation for (T) and get
(T)=(4m)
(1−D)/2
4−D
20b
0
T
D
√
T
c
˛
0
−
, (10.54)
where 2 = [1 − (4 − D)/5]
−1
. As has already been
mentioned, strictly speaking this result was carried
out for " =4−D 1, so it is confident up to the
first in " expansion only: =1/2+"/10. Neverthe-
less, extending it to " =1(D = 3) one can obtain
3
=3/5.
Let us pass to the calculation of the critical expo-
nent of the heat capacity in the immediate vicinityof
the transition. Forthis purpose one can calculate the
second derivative of equation (10.43) with respect
to :
@C()
@
= T
2
D
D−1
˛
2
()
˛()T
c
+
2
4m
2
. (10.55)
The heat capacity renormalized by fluctuations has
the value C( = 0), which is the result of integration
over all fluctuationdegrees of freedom.Carrying out
382 A.I. Larkin and A.A.Varlamov
the integrationof (10.55)over all
−1
one can di-
vide the domain of integration on the right hand side
in two:
−1
(T)and
−1
(T)
−1
.Inthecal-
culation of the integral over the region
−1
(T)
the inequality ˛()T
c
2
4m
holds, and the func-
tion ˛() can be omitted in the denominator. In the
numerator of (10.55) one can use for ˛()theso-
lution (10.53). In the region
−1
(T)onehasto
use the partial solution (10.49) for˛() and can find
that the contribution of this domain has the same
singularity as that from the region
−1
(T), but
with a coefficient proportional to (4−D)
2
= "
2
,hence
negligible in our approximation. The result is
C( =0)=˛
2
0
(4mT)
2
D
1
5
4
5
(4 − D)
b
0
4/5
×
5
4−D
4−D
5
(T) .
Substituting the expression for (T) one can finally
find
C =2
12/5
˛
2
0
5
D
m
2
T
2
b
4
0
(4 − D)
1
5
−˛
, (10.56)
confirmingthe validity of the scaling hypothesis and
the relation(10.39).Thecriticalexponentin (10.56) is
˛ =
(4 − D)
10[1 − (4 − D)/5]
≈ "/10 .
Onecanseethat,generallyspeaking,thecriticalex-
ponents and ˛ appear in the form of series in pow-
ers of ".Morecumbersome calculations permit find-
ing the next approximations for them in " =4−D.
Nevertheless it is worth mentioning that even the
first approximation, giving
3
=3/5and˛
3
=1/10
for " = 1, is already weakly affected by the following
steps of the expansion in powers of " [23].
One can notice that the exercise performed in this
section has more of an academic than a practical
character.Indeed, the results obtained turn out to be
applicableto the analysis of thecriticalregion ofa3D
superconductor only if Gi is so small that the theo-
retical predictionsare hardly experimentally observ-
able. Nevertheless, we demonstrated the RG method,
which helps one to see the complete picture of the
fluctuations manifestation in the vicinity of the crit-
ical temperature.
10.2.4 Fluctuation Diamagnetism
Qualitative Preliminaries
In this section we discuss the effectof fluctuations on
the magnetization and the susceptibility of a super-
conductor above the transition temperature. Being
the precursor effect for the Meissner diamagnetism,
the fluctuation induced magnetic susceptibility has
to be a small correction with respect to the diamag-
netism of a superconductor,butit can be comparable
to or even exceed the value of the normal metal dia-
magnetic or paramagnetic susceptibility and can be
easily measured experimentally.As was already men-
tioned in the Introduction the temperature depen-
dence of the fluctuation induced diamagnetic sus-
ceptibility can be qualitatively analyzed on the basis
of the Langevinformula,butsome precautionsin the
case of low dimensional samples have to be taken.
As regards the 3D case we would like to mention
here that expression (10.12), presented in terms of
(T), has a wider region of applicability than the
GL one. Namely, the scaling arguments are also valid
for diamagnetic susceptibility and one can write the
general relation
(3)
∼ −e
2
T(T) ∼ −
P
−1/2
1
1, Gi
Gi
1/2−
, Gi ,
(10.57)
which is also valid in the region of critical fluctua-
tions in the immediate vicinity of the transition tem-
perature. Here, in order to define the scale of fluc-
tuation effects, we have introduced the Pauli para-
magnetic susceptibility
P
= e
2
v
F
/4
2
.Moreover,
the Langevin formula permits us to extend the esti-
mation of the fluctuation diamagnetic effect to the
other side beyond the GL region: to high tempera-
tures T T
c
. The coherence length far from the
transition becomes a slow function of temperature.
In a clean superconductor, farfrom T
c
, (T) ∼ v
F
/T,
so one can write
(3c)
(T T
c
) ∼ −e
2
T(T) ∼ −
P
(10.58)
and see that the fluctuation diamagnetism turns out
to be of the order of the Pauli paramagnetism even
10 Fluctuation Phenomena in Superconductors 383
far fromthetransition.Moreprecisemicroscopic cal-
culations of
(3)
(T T
c
) lead to the appearance of
ln
2
(T/T
c
) in the denominator of (10.58).
In the 2D case, (10.12) is applicable for the esti-
mation of
(2)
in the case when the magnetic field
is applied perpendicular to the plane, permitting 2D
rotations of fluctuation Cooper pairs in it:
(2c)
(T) ∼ e
2
n
m
R
2
∼e
2
T
2
(T) ∼ −
P
E
F
T − T
c
.
(10.59)
This result is valid for a wide range of temperatures
and can exceed the Pauli paramagnetism by factor
E
F
T
even far from the critical point (we consider the
clean case here).
For a thin film (d (T)) perpendicular to the
magnetic field the fluctuation Cooper pairs behave
likeeffective2Drotators,and(10.12)canstill beused,
though one has to take into account that the suscep-
tibilityin thiscase is calculated per unit square of the
film. So for the realistic case (from the experimen-
tal point of view) of the dirty film, one just has to
use in (10.59)the expression (10.6) forthe coherence
length:
(2d)
∼
e
2
T
d
2
(T) ∼ −
P
l
d
T
c
T − T
c
. (10.60)
Now let us discuss the important case of a layered
superconductor(for example,a high temperature su-
perconductor). It is usually supposed that the elec-
trons move freely in conducting planes separated by
a distance s. Their motion in the perpendicular di-
rection has a tunneling character, with effective en-
ergy J.The related velocity and coherence length can
be estimated as v
z
= @E(p)/@p
⊥
∼ J/p
⊥
∼ sJ and
z,(c)
∼ sJ /T for the clean case. In the dirty case the
anisotropy can be taken into account in the spirit of
(10.6), yielding
z,(d)
∼
√
D
⊥
/T ∼ sJ
√
/T.
We start from the case of a weak magnetic field
applied perpendicular to layers. The effective area of
a rotating fluctuation pair is
x
()
y
(). The density
of Cooper pairs in the conducting layers (10.10) has
to be modified for the anisotropic case. Its isotropic
3D value is proportional to 1/(), which now has to
be read as ∼ 1/
x
()
y
(). The anisotropy of the
electron motion leads to a concentration of fluctua-
tion Cooper pairs in the conducting layers,and hence
to an effectiveincrease of the Cooper pairs density of
x
()
y
()/
z
() times its isotropic value. This in-
crease is saturated when
z
() reaches the interlayer
distance s, so finally the anisotropy factor appears in
the form
x
()
y
()/ max{s,
z
()},andthesquare
root in its numerator is removed in the Langevin for-
mula (10.12), which is rewritten for this case as
(layer,⊥)
(, H → 0) ∼ −e
2
T
x
()
y
()
max{s,
z
()}
. (10.61)
The existence of a crossover between the 2D and 3D
temperature regimes in this formula is evident: as
the temperature tends to T
c
the diamagnetic suscep-
tibility temperature dependence changes from 1/ to
1/
√
. This happens when the reduced temperature
reaches its crossover value
cr
= r
z
(
cr
) ∼ s
.The
anisotropy parameter
r =
4
2
z
(0)
s
2
=
J
2
T
⎧
⎪
⎨
⎪
⎩
4
, T 1
7(3)
8
2
T
, T 1
(10.62)
plays an important role in the theory of layered su-
perconductors.
12
It isinterestingtonotethatthisintrinsiccrossover,
related to the spectrum anisotropy, has an oppo-
site character to the geometric crossover that occurs
in thick enough films when (T) reaches d.Inthe
latter case the characteristic 3D 1/
√
-dependence
takes place far enough from T
c
(where (T) d),
is changed to the 2D 1/ law (see (10.60)) in the
immediate vicinity of transition (where (T)
d) [24]. It is worth mentioning that in a strongly
anisotropic layered superconductor the fluctuation-
induced susceptibility may considerably exceed the
normal metal diamagentic and paramagnetic effects
even relatively far from T
c
[25,26].
Let us consider a magnetic field applied along the
layers. First it is necessary to mention that the fluc-
tuation diamagnetic effect disappears in the limit
J ∼
z
→ 0.Indeed,fortheformationof a circulating
12
We use here a definition of r following from microscopic theory (see Sect. 10.6).

384 A.I. Larkin and A.A.Varlamov
current it is necessary to tunnel twice, so
(layer,)
∼ −e
2
T
2
z
max{s,
z
(T)}
∼ −
P
sJ
v
F
J/T
√
max{
√
, J/T}
.
In the general case of an anisotropic superconductor,
choosing the z-axis along the direction of magnetic
field H, the following extrapolation of the results ob-
tained may be written:
∼ − e
2
T (10.63)
×
2
x
()
2
y
()
max{a,
x
()}max{b,
y
()}max{s,
z
()}
.
This general formula is useful for the analysis of the
fluctuation diamagnetism of anisotropic supercon-
ductors or samples of some specific shape: granular,
quasi-1D,quasi-2D,and3D.It is also applicable to the
case of a thin film (d
z
()) placed perpendicular
to the magnetic field: it is enough to replace
z
()by
d in (10.64). Nevertheless, (10.64) cannot be applied
to the cases of thin films in parallel fields, wires and
granules.In those cases theLangevin formula (10.12)
can still be used with the replacement of
9
R
2
:
→ d
2
:
(D)
∼ −
P
T
v
F
2−D
d
D−1
∼
D/2−1
.
The magnetic field dependence of the fluctuation
part of free energy in these cases is reduced only
to account for the quadratic shift of the critical tem-
perature versus magnetic field.
For 3D systems or in the case of a film in a per-
pendicular magnetic field the critical temperature
depends on H linearly, while the magnetic field de-
pendent part of the free energy for H H
∗
c2
(−)(the
line H
∗
c2
(−) is mirror-symmetric to the H
c2
()with
respect to y-axis passing through T = T
c
) is propor-
tional to H
2
. This is why the magnetic susceptibility
is determined by (10.64) for weak enough magnetic
fields H ¥
0
/[
x
()
y
()] = H
c2
() H
c2
(0) only.
In the vicinity of T
c
these fields are small enough.
Zero-Dimensional Diamagnetic Suscept ibility
For quantitative analysis of the fluctuation diamag-
netism we start by writing down the GL functional
for the free energy (see (10.16)) in the presence of
the magnetic field
F [¦ (r)] = F
N
+
dV
a|¦ (r)|
2
+
b
2
|¦ (r)|
4
+
1
4m
|
(
−i∇−2eA
)
¦ (r)|
2
+
B
2
8
−
H · B
4
,
(10.64)
where A is vector potential.As long as fluctuation ef-
fects are comparatively small, the average magnetic
field in the metal B may be assumed to be equal to
the external field H. Thus we omit the last two terms
in (10.64) (see later on).
The fluctuation contribution to the diamag-
netic susceptibility in the simplest case of a “zero-
dimensional” superconductor (spherical supercon-
ducting granule of diameter d ()) was consid-
ered by V. Shmidt [11]. In this case the order param-
eter does not depend on the space variables and the
free energy can be calculated exactly for all temper-
atures including the critical region in the same way
aswasdoneforthecaseoftheheatcapacityinthe
absence of a magnetic field. Formally the effect of a
magnetic field in this case is reduced to the renor-
malization of the coefficient a, or, in other words, to
the suppression of the critical temperature. This is
why one can use the same formula (10.23) for the
partition function with the critical temperature T
c
shifted by magnetic field as:
13
T
c
(H)=T
c
(0)
1−
4
2
2
¥
2
0
A
2
. (10.65)
Here ¥
0
=
e
is the magnetic flux quantum and ...
means the averaging over the sample volume.
Such a trivial dependence of the properties of 0D
samples on magnetic field immediately allows one to
understand its effect on the heat capacity of a gran-
ular sample. Indeed, with the growth of the field the
13
Let us stress the difference between the H
2
shift of the critical temperature for a zero-dimensional granule and the
linear shift in the case of bulk material.
10 Fluctuation Phenomena in Superconductors 385
temperature dependence of the heat capacity pre-
sented in Fig. 10.1 just moves in the direction of
lower temperatures.
In the GL region Gi
(0)
one can write the
asymptotic expression (10.23) for the free energy:
F
(0)
(, H)=−T ln
˛
+
4
2
2
¥
2
0
A
2
.
In the case of a spherical particle the relation A
2
=
(
1
2
H × r)
2
=
1
40
H
2
d
2
can be used in full analogy
with the calculation of the moment of inertia of a
solid sphere.In this way an expression for the0D fluc-
tuation magnetization valid forall fieldsH H
c2
(0)
can be found:
M
(0)
(, H)=−
1
V
@F
(0)
(, H)
@H
=−T
6
2
5¥
2
0
d
+
2
2
10¥
2
0
H
2
d
2
H . (10.66)
Onecanseethatthefluctuationmagnetizationturns
out to be negative and linear up to some crossover
field, which can be called the temperature dependent
upper critical field of the granule H
c2(0)
() ∼
¥
0
d()
=
d
H
c2
(0)
√
at which it reaches a minimum.At higher
fields H
c2(0)
() H H
c2
(0) the fluctuation mag-
netization of the 0D granule decreases as 1/H.In
the weak field region H H
c2(0)
() the diamagnetic
susceptibility is:
(0)
(, H)=−
6T
2
0
5¥
2
0
d
1
≈ − · 10
2
P
d
1
,
which coincides with our previous estimate in its
temperature dependence but the numerical factor
found is very large.Let us underline that the temper-
ature dependence of the 0D fluctuation diamagnetic
susceptibility turns out to be less singular than the
0D heat capacity correction:
−1
instead of
−2
.
The expression for the fluctuation part of free en-
ergy (10.28) is also applicable to the cases of a wire or
a film placed in a parallel field; as was already men-
tioned above all its dependence on magnetic field
is manifested by the shift of the critical tempera-
ture (10.65). In the case of the wire in a parallel field
one has to choose the gauge of the vector-potential
A =
1
2
H × r yielding
9
A
2
:
(wire,)
=
H
2
d
2
32
(the calcula-
tion of this average is analogous to that of the mo-
ment of inertia of a solid sphere). For a wire in a
perpendicular field, or a film in a parallel field, the
gauge has to be chosen in the form A =(0, Hx, 0) (to
avoid the appearance of currents perpendicular to
surface). One can find
9
A
2
:
(wire,⊥)
=
H
2
d
2
16
for a wire
and
9
A
2
:
(film,)
=
H
2
d
2
12
for a film.
Calculating the second derivative of (10.28) with
the appropriate magnetic field dependencies of the
critical temperature one can find the following ex-
pressions for the diamagnetic susceptibility:
(D)
()=−2
T
v
F
(10.67)
×
P
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
1
√
, wire in parallel field
2
√
, wire in perpendicular field
d
3
ln
1
, film in parallel field.
GL Treatment of Fluctuation Magnetization
Let us analyze quantitatively, on the basis of the GL
functional, the temperature and field dependencies
of the fluctuation magnetization. We will carry on
the discussion for a layered superconductor. As has
already been mentioned this system has great prac-
tical importance because of its direct applicability to
high temperature superconductors,wherethe fluctu-
ation effects are very noticeable. Moreover, the gen-
eral results obtained will allow us to analyze 3D and
2D situations as limiting cases. The effects of a mag-
netic field are more pronounced for perpendicular
orientation, so let us consider this case first.
The generalization of the GL functional for a lay-
ered superconductor (Lawrence–Doniach (LD) func-
tional [27]) in a perpendicular magnetic field can be
written as

386 A.I. Larkin and A.A.Varlamov
F
LD
[
¦
]
=
l
d
2
r
a |¦
l
|
2
+
b
2
|¦
l
|
4
(10.68)
+
1
4m
∇
−2ieA
|¦
l
2
+ J |¦
l+1
− ¦
l
|
2
,
where ¦
l
is the order parameter of the l-th supercon-
ducting layer and the phenomenological constant J
is proportional to the Josephson coupling between
adjacent planes. The gauge with A
z
=0ischosen
in (10.69). In the immediate vicinity of T
c
the LD
functional is reduced to the GL one with the effec-
tive mass M =(4J s
2
)
−1
along c-direction, where s
is the inter-layer spacing. One can relate the value
of J to the coherence length along the c-direction:
J =2˛T
c
2
z
/s
2
. Since we are dealing with the GL re-
gion the fourth order term in (10.69) can be omitted.
As it is well known the Landau representation is
the most appropriate one for problems related with
the motion of a charged particle in a uniform mag-
netic field. Basic wave functionscan be chosen as the
products of a plane wave propagating along the mag-
netic field direction and a Landau state wave func-
tions
n
(r). Let us expand the order parameter ¦
l
(r)
on the basis of these eigenfunctions:
¦
l
(r)=
SH
¥
0
n,k
z
¦
n,k
z
n
(r)exp(ik
z
l). (10.69)
The factor SH/¥
0
takes into account the degeneracy
of Landau state n while k
z
is the momentum compo-
nent along the direction of the magnetic field.Substi-
tuting this expansion into (10.69)onecan find the LD
free energy as a functional of the ¦
n,k
z
coefficients:
F
LD
¦
n,k
z
=
n,k
z
˛T
c
+
H
2m¥
0
n +
1
2
(10.70)
+ J
(
1−cos(k
z
s)
)
|¦
n,k
z
|
2
.
In complete analogy with the case of an isotropic
spectrum the functional integral over the order pa-
rameter configurations ¦
n,k
z
in the partition func-
tion can be reduced to a product of ordinary Gaus-
sian integrals, and the fluctuation part of the free
energy in a magnetic field takes the form:
F (, H)=−
SH
¥
0
T
n,k
z
ln (10.71)
×
T
˛T
c
+
H
2m¥
0
n +
1
2
+ J
(
1−cos(k
z
s)
)
.
The sum in (10.72) is evidently divergent and in or-
der to regularize it we introduce a formal cut-off pa-
rameter n
c
, the number of the last Landau level, at
which the summation is interrupted. Its value can
be evaluated by appealing to the restrictions of the
GL theory, which breaks down for short wave length
fluctuations and is valid for k k
max
,where
k
2
max
/4m ∼ ˛T . (10.72)
In terms of the Landau level summation this condi-
tioncanberewrittenas:
n
c
∼ ˛T/!
c
∼ ˛Tm¥
0
/H
∼ ¥
0
/
2
xy
H
∼ H
c2
(0)/H .
(10.73)
The formal divergence of the GL free energy does not
effect on such observable properties as the heat ca-
pacity and the diamagnetic susceptibility. Being the
second derivatives of the free energy these physical
values are well defined, the momentum (or Landau
levels) summation converges well for them. Never-
theless, the problem of regularization arises for ex-
ample in calculation of the 3D fluctuation magne-
tization. Being only the first derivative of the free
energy it turns out to be also divergent and must be
cut off.Let us stress that the ultraviolet divergence of
the fluctuation part of the GL free energy is the re-
sult of the limitedness of the GL functionalapproach,
unapplicable to the description of short wavelength
fluctuations. This problem does not appear at all in
the consistent microscopic theory, which correctly
accounts for the short wavelength fluctuations and
does not require any renormalization procedure.
In the limit of weak fields one can carry out the
summation over the Landau states by means of the
Euler–Maclaurin transformation
10 Fluctuation Phenomena in Superconductors 387
N
n=0
f (n)=
N+1/2
−1/2
f (n)dn
−
1
24
f
(N +1/2) − f
(−1/2)
,
and obtain
F(, H)=F(, 0) +
STH
2
24m¥
2
0
/s
−/s
N sdk
z
2
(10.74)
×
1
˛T
c
+J
(
1−cos(k
z
s)
)
.
Here N is the total number of layers. After the mo-
mentum integration one gets:
F(, H)=F(, 0) +
VH
2
24m˛s¥
2
0
1
√
( + r)
,
with the anisotropy parameter defined as
14
r =
2J
˛T
=
4
2
z
(0)
s
2
. (10.75)
The magnetic susceptibility in a weak field turns
out [28,29] to be
(layer,⊥)
=−
e
2
T
3s
2
xy
√
( + r)
. (10.76)
These results confirm the qualitative estimation
(10.61), additionally providing the exact value of the
numerical coefficient and the temperature depen-
dence in the crossover region. In the limit r
(10.76) transforms into the diamagnetic susceptibil-
ity of the 3D anisotropic superconductor [30].
For a film of thickness d the integral over k
z
in ex-
pression (10.75) has to be replaced by a summation
over the discrete k
z
and when
z
(T) d only the
term with k
z
= 0 has to be taken into account:
(film,⊥)
=−
e
2
T
3d
2
xy
. (10.77)
Note that these formulas predict a nontrivial increase
of diamagnetic susceptibility for clean metals [29].
The usual statement that fluctuations are most im-
portant in dirty superconductors with a short elec-
tronic mean free path does not hold in the particular
case of susceptibility,because here turns out to be
in the numerator of the fluctuation correction.
Now we will demonstrate that, besides the
crossovers in its temperature dependence, the fluc-
tuation induced magnetization is also a nonlinear
function of magnetic field, and these nonlinearities,
different for various dimensionalities, take place at
relatively low fields. This manifestation of the non-
linear regime in fluctuation magnetization, which
is strong in comparison with the expected scale of
H
c2
(0), and hence, field-dependent fluctuation sus-
ceptibility,wasthe subject of the intensive debates in
early 1970s [30–39] (see also the older excellent re-
view of W.J.Skocpol and M. Tinkham [40]) and after
the discovery of HTS [41–44] (see also the very re-
cent detailed essay of T. Mishonov and E. Penev [45]
and references therein). We will mainly follow here
the paper of Buzdin et al. [46], dealing with the fluc-
tuation magnetization of a layered superconductor,
whichpermitsobserving in a unique way all varieties
of the crossover phenomena in temperature and the
magnetic field.
Let us go back to the general expression (10.72)
and evaluate it without taking the magnetic field to
small.The difficulty in dealing with it consists in the
divergence of the sum over Landau levels n.Thisdi-
vergence can be regularized (see [45,47]), but let us
observe that in order to calculate the magnetization
we must know the magnetic field dependent part of
the free energy only.A very convenient method to by-
passthedivergenceproblem[48]istocalculatethe
difference F(H)−F(0), turning the sum over Landau
states in F(, 0) into an integral and then, in turn,
turning this integral into a sum of integrals over the
14
Let us stress the difference between J and J in the two definitions (10.62) and (10.75) of the anisotropy parameter r.
The first one was introduced as the electron tunneling matrix element, while the second one enters in the LD functional
as the characteristic Josephson energy for the order parameter. Later on, in the framework of the microscopic theory, it
will be demonstrated that,in accordance with our qualitative definition, r ∼J
2
,whileJ turns out to be proportional to
J
2
too.In the dirty case it depends on the relaxation time of the electron scatteringon impurities: J ∼ ˛J
2
max{, 1/T}.
Hence both definitions (10.62), appearing in the qualitative consideration, and (10.75), following from the LD model,
are consistent.

388 A.I. Larkin and A.A.Varlamov
Fig. 10.3. Schematic representation of the dif-
ferent regimes for fluctuation magnetization in
the (H, T)diagram.ThelineH
∗
c2
(T) is mirror-
symmetric to the H
c2
(T) line with respect to a
y-axis passing through T = T
c
.Thislinede-
fines the crossover between linear and nonlin-
ear behavior of the fluctuation magnetization
above T
c
unit length intervals x ∈ [n −1/2, n +1/2]. Then
F(, 0) = − lim
H→0
VH
¥
0
T
/s
−/s
dk
z
2
∞
n=0
1/2
−1/2
dx
×ln
T
˛T
c
+
H
2m¥
0
x + n +
1
2
+J
(
1−cos(k
z
s)
)
.
and by introducing the dimensionless variable
15
h =
H
H
c2
(0)
, H
c2
(0) = 2m˛T
c
/e = ¥
0
/2
2
xy
,
(10.78)
one can write
F (, H)−F(, 0) = −
TV
2s
2
xy
h
−
dz
n=0
1/2
−1/2
dx ln
×
(2n +1+2x)h + r/2(1 − cosz)+
(2n +1)h + r/2(1 − cosz)+
. (10.79)
Performing the integrations over z and x in (10.79)
and differentiating with respect to h we finally obtain
a very convenient general expression for the fluctua-
tion magnetization in a layered superconductor:
M(, H)=
T
¥
0
s
∞
n=0
n ln
'(R
n
+1)
'(R
n
)
(10.80)
+ln
'(R
n
+1)
'(R
n
+1/2)
−
n +1/2
(R
n
+1/2)
2
−
2
with '(x)=x +
x
2
−
2
, R
n
= n + /2h + and
= r/2h. The sum in (10.81) converges as 1/n
2
and
it provides a volume magnetization expression that
can be compared with experiment.
Let us comment on the different crossovers in the
M(, H) field dependence analyzing the general for-
mula (10.81). Let us fix the temperature r.In
this case the c-axis coherence length exceeds the in-
terlayer distance (
z
s)andintheabsenceofa
magnetic field the fluctuation Cooper pairs motion
has a 3D character. Supposing the magnetic field to
be not too high (h r) we may perform an expan-
sion in (10.81) in 1/ and obtain
M
(3)
( r, h r)=
T
√
2h
1/2
¥
0
z
(10.81)
×
n
(
n +1
)
n +1+
2h
1/2
−n
n +
2h
1/2
−
3
2
(n +1+
2
3h
)
n +
1
2
+
2h
.
For weak fields (h ) the magnetization grows lin-
early with magnetic field, justifying our preliminary
qualitative results. Nevertheless, this linear growth
is changed to the nonlinear 3D high field regime
M ∼
√
H already in the region of a relatively small
fields H
c2
() H ( h). The further increase of
magnetic field leads to the next crossover in the mag-
netization field dependence at h ∼ r. However the
expression (10.81) was obtained in the assumption
15
Let us recall that the exact definition of H
c2
(0) contains the numerical coefficient A(0) (see footnote3).
