Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

9 Principles of Josephson-Junction-Based Quantum Computation 349

pulsed gate.The repetition time of 64 ns between the

pulses is long enough (compared with the quasipar-

ticle relaxation time of 10 ns) to let the system decay

through a Josephson-quasiparticle, and give rise to

a probe current proportional to p

1,2

.Theestimated

amplitude of the applied pulses is V

≈ 30 mV.

The results obtained in this way are presented in

Fig.9.38.First,bycontrollingN

orN

,individually,

the system can be brought to the points R or L; one

thenperformssingle qubit measurementsby exciting

autonomous oscillations in one of the qubits (upper

two traces in Fig. 9.38).The spectra of the oscillations

can be fitted to a cosine function with an exponential

decaytimeofabout2.5ns.Thespectraoftheoscilla-

tions (right panels of Fig. 9.38) obtained by Fourier

transforming contain one pronounced component at

13.4GHz for the firstqubitandat 9.1 GHz forthe sec-

ond qubit. These values are identified with E

and

. From the experiments (see, for example, [82])

one concludes that the values obtained are close to

those expected for the device fabrication parameters

(i.e., overlap area and oxidation conditions).

By controlling both N

and N

, the system can

be driven to the vicinityof the co-resonance point,X,

and the induced quantum oscillations traced using

the same technique. The oscillation patterns, shown

in the lower two traces in Fig. 9.38 (with the Fourier

transforms given to the right), are then more com-

plex; two clear frequencies now appear in the spec-

trum. For the above parameters (E

=13.4 GHz and

=9.1 GHz) measured in the single qubit exper-

iments, and a value for E

=15.7GHzestimated

from independent measurements of dc current–

voltage/gate-voltage characteristics, the two peaks in

the spectrum are close to the expected frequencies

§ + " and § − " predicted from Eq. (9.70); these fre-

quencies are indicated by the arrows and dotted lines

in lower right of Fig. 9.38. The decay time (0.6 ns)

of the coupled oscillations near X is shorter than

that observed for the independent oscillations near

R or L, as is expected because an extra decoherence

channel appears for each qubit after coupling it to

its neighbor. The amplitudes of the spectral peaks do

not agree that well with those predicted by Eq. (9.70).

This is attributed to the non-ideal pulse shape (fi-

nite rise/fall time 35 ps), and the fact that a small

shift of N

and V

off the co-resonance drastically

changes the oscillation pattern. Also, even far from

the co-resonance, a small contribution to the initial

state is still observed which arises from charge states

other than |00 distorting the oscillations. Numer-

ical simulations have been performed of the oscil-

lation pattern, taking into account a realistic pulse

shape and an initial condition corresponding to a

non-pure |00 state, but assuming the system is ex-

actly at co-resonance. The resulting fits are shown in

Fig. 9.38 as solid lines. A slightly different value of

=14.5 GHz, close to the value estimated above

from the d.c. measurements, gives better agreement

with the experimental data.

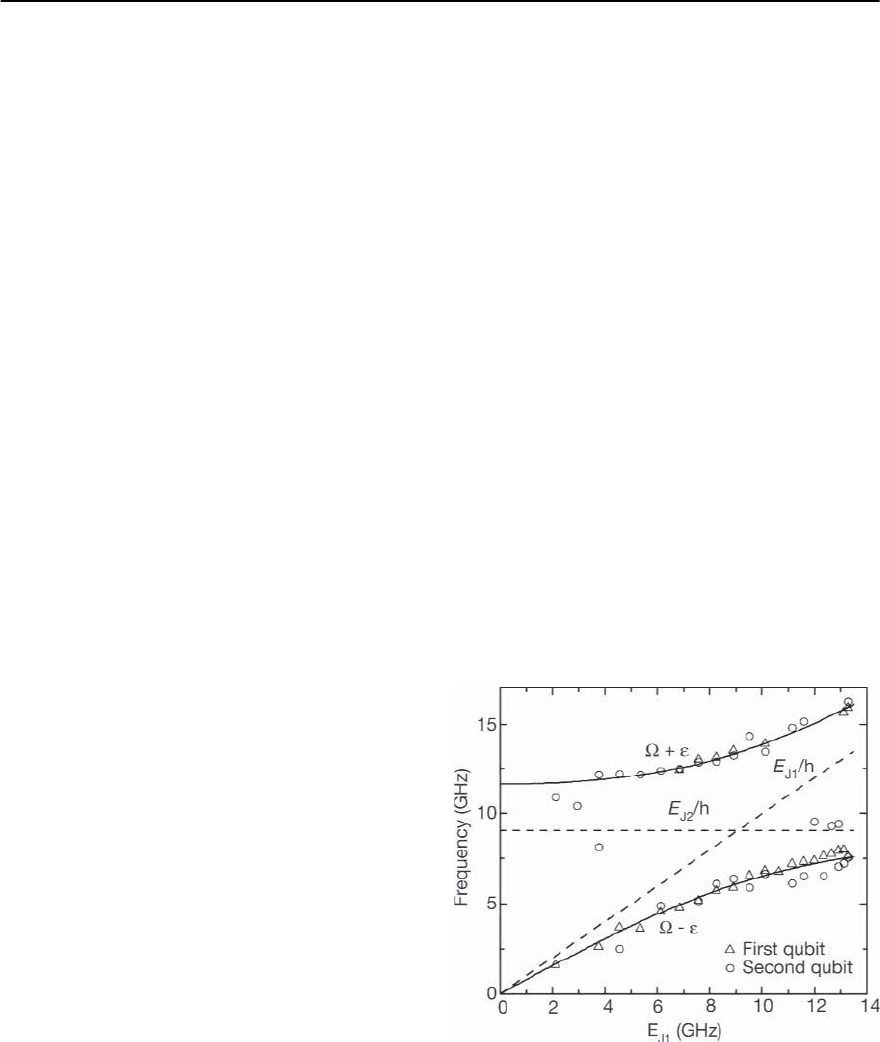
Finally,the dependence of the oscillation frequen-

cies on E

was controlled by a weak magnetic field

(up to 20 G). The results are shown in Fig. 9.39. The

plot contains the data from both qubits represented

by open triangles (first qubit) and open circles (sec-

ond qubit). Without coupling (E

= 0), the single

peaks in each qubit would follow the dashed lines

with an intersection at E

= E

. The coupling intro-

duced modifies this dependence by creating a gap,

and shifting the frequencies to higher and lower val-

ues; the spacing between the two branches is equal

to E

/2h when E

= E

.Acomparisonoftheob-

Fig. 9.39. E

-dependence of the spectrum components ob-

tained by Fourier transform of the oscillations at the co-

resonance

350 S.E. Shafranjuk and J.B. Ketterson

Fig. 9.40.

Possible sources of de-

coherence

served dependence with the prediction of Eq. (9.68)

(given by solid lines) gives excellent agreement. The

observed quantum coherent dynamics of coupled

qubits in the vicinity of the co-resonance, in particu-

lar,the double-frequency structureof the probability

oscillations in both qubits,structureof the probabil-

ity oscillations in both qubits,and frequency ’repul-

sion’ at E

≈ E

(see Fig. 9.38b) indicates that the

two qubits become entangled during the course of

coupled oscillations, although a direct measurement

of the degree of entanglement was not possible. Sim-

ple calculations [83] based on the standard expres-

sion for the entanglement of the pure states show

that,with an ideal pulse shape and the|00initialcon-

dition, the wave function given in Eq. (9.69) evolves

through a maximally entangled state in the case of

equal Josephson energies.The numerical simulations

confirm that the amount of entanglement does not

decrease significantly when realistic experimental

conditionsare taken into account.The relativelylarge

observed oscillation amplitude (about50% of the ex-

pectedvalue) also suggests the existence of entangled

states even in multi-pulse averaged experiments.For

decoherence effects see Fig. 9.40.

9.5 SISIS Two-Qubit Gate with Intrinsic

Coupling

In majority of realistic systems under consideration,

there are usually several discrete energy levels. How-

ever a qubit utilizes only two of these levels and

therefore care must be taken to isolate these lev-

els from the remaining Hilbert space. We consid-

ered a multi-terminal double barrier SISIS junction

(S and I denote a superconductor and an insulat-

ing barrier respectively) is suggested as a two-qubit

gate with tunable intrinsic coupling. The presenta-

tion in this section is based on [84]. Two quantum

wells are formed in vicinitiesof the left and right SIS

subjunctions.Thisgives two individual qubits,which

are intrinsically coupled via the middle S layer due to

phase coherence. The inter-qubit coupling J is tuned

by two bias supercurrents I

and I

across each of

the SIS subjunctions independently. Additional cou-

pling is accomplished by transport supercurrents I

along adjacent S layers. Using a microscopic model

we compute major qubit characteristics and study

sources of the intrinsic decoherence. One computes

the entanglement of the two qubit states, leakage

and fidelity characteristics versus J,anddiscussthe

readout process. Each qubit is a two-state quantum

9 Principles of Josephson-Junction-Based Quantum Computation 351

system, which behaves like a spin-1/2 particle and

can be entangled with other qubits. In recent ex-

periments [85,86] a quantum-coherent dynamics of

two Josephson qubits coupled through a capacitance

was studied. A tunable interaction between different

types of Josephson qubits was examined also theo-

retically (see [76,87] and the references therein).The

qubit gate [88,89] consisted of two current-biased

Josephsonjunctions coupledvia a capacitance,which

allowed performing of arbitrary two-qubit quantum

logic operations (see Fig. 9.40).

The method of capacitive coupling has, however,

certain disadvantages. In particular, additional cir-

cuit elements and wiring serve as potential sources

of disturbance in the system: the electric charges,

accumulated on the capacitance, disturb the quan-

tum states and cause errors during quantum logic

operations. An alternative way to introduce a tun-

able coupling between different quantum subsys-

tems is exploiting of a bias-tuned intrinsic coupling

taking place in multilayered multiterminal struc-

tures [90–92]. Though general properties of the in-

trinsic entanglement in a solid state device were con-

sidered earlier (see, e.g.,[93] and references therein),

its implementation to the two-qubit gates is not well

known yet.

We payed our attention to a simple two-qubit gate

based upon intrinsic properties of a double-barrier

multi-terminal SISIS junction(S is the superconduc-

tor, I is the insulating barrier) with a proximity-type

coupling between the left and right SIS subjunctions

(see Fig.9.4) across their common S layer.Elementary

quantum logic operations on qubits [75,94–98] are

associated with controlled manipulations involving

two states 0 and 1 ofthesamequbit,thesuperpo-

sition of which forms a mixed state | ¦ .

Quantum computing presumes also superposi-

tion | ¥

1,2

of the states | ˛

and | ˇ

of two different

qubits, 1 and 2. An ideal two-qubit Hamiltonian in

spin-1/2 notations takes the form [3]



k=1, 2

(k)

ˆ

+ 

(k)

ˆ

+ ˆ˛

]





i ˆ



⊗



i ˆ



(9.71)

where "

(k)

and 

(k)

are the energy level spacing

and the inter-level tunneling matrix element in the

k-th qubit, ˆ

and ˆ

, are Pauli matrices associ-

ated with the first and second qubits; J

is the

inter-qubit coupling energy, {n, m} = {x, y, z}.Each

of the qubits is independently controlled by fields

ˆ˛

= ˛

exp( ˆ



(t)), where ˛

and 

are control

field amplitudes and phases, and k =1, 2. For con-

trolled manipulations of the qubit the coefficientsof

the Hamiltonian are modified by adiabatic change

of the Josephson supercurrents. The adiabaticity is

required to eliminate transitions between different

two-qubit gate states. The parameters of Eq. (9.71)

depend also on particular design of the qubit gate.

Each of the qubits in the two-qubit gate described

by Eq. (9.71) should behave individually. One as-

sumes that r.f. control pulses address both qubits

with no disturbance of other circuit elements. The

two qubits labeled as 1 and 2 are builtusing the tilted

washboard Josephson energy potentials U

)and

), where '

and '

are the phase differences

across the left (1) and right (2) SIS sub-junctions.

The sets of quantized energy levels QL positioned

at "

(

)

(l is the qubit index and n is the level quan-

tum number) are formed in the washboard quantum

wells U

and U

.ThetiltingofU

and U

is controlled

by the bias supercurrents I

and I

as shown in the

Fig. 9.41. We will see that directions and magnitudes

of I

and I

not only affect the inter-level spacing

= "

− "

(l =1, 2) in both the qubits but actually

determine the strength of the inter-qubit interaction

. In this way one accomplishes arbitrary single-

and two-qubitquantumlogic operations with apply-

ing appropriate r.f. and d.c. bias currents to the SIS

sub-junctions.

9.5.1 Proximity Coupling in a Multilayered Junction

The coupling between the left and right SIS sub-

junctions of the SISIS junction (see Figs. 9.41, 9.42)

is conveniently described in terms of Andreev reﬂec-

tion. Here we are interested in a non-local process

when an incoming electron and the reﬂected hole be-

long to different electrodes spatially separated by a

distance ∼  ,where being the superconducting co-

herence length (see, i.e., [91] and references therein).

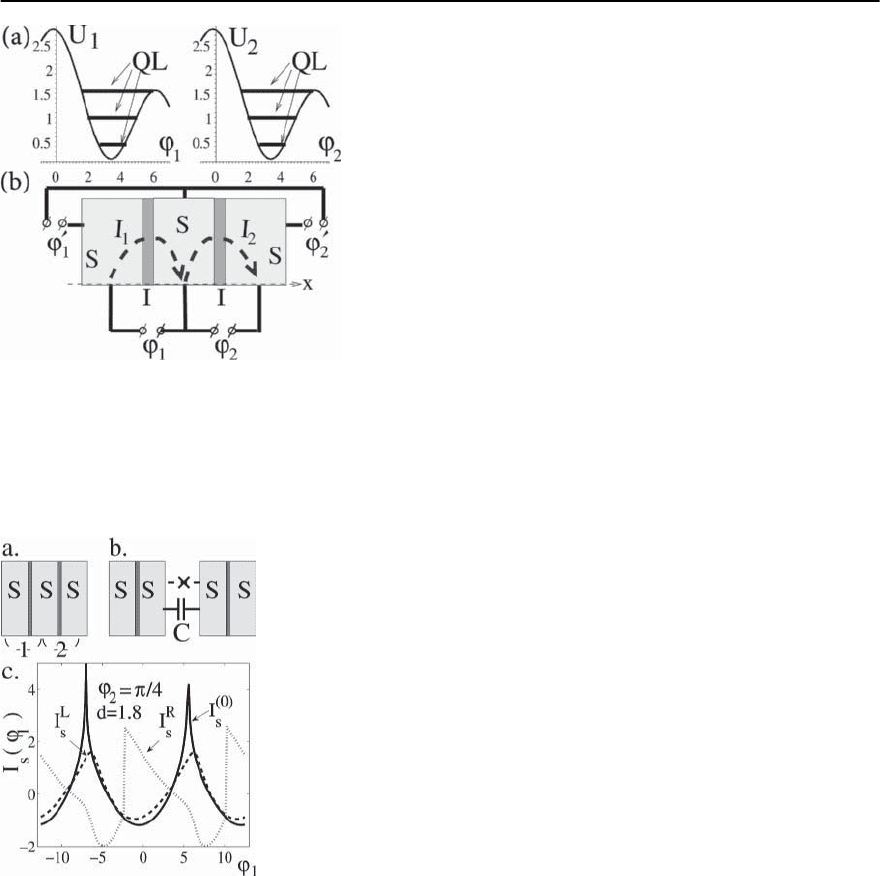
352 S.E. Shafranjuk and J.B. Ketterson

Fig. 9.41. (a) The quantized levels (QL) formed inside the

quantum wells U

and U

controlled by bias supercurrent

and I

across the SIS subjunctionsof a multiterminal SI-

SIS junction. The phase differences '

and '

if transport

supercurrents I

ﬂow along the S electrodes. (b)Schematic

illustration of the current biasing of the SISIS junction

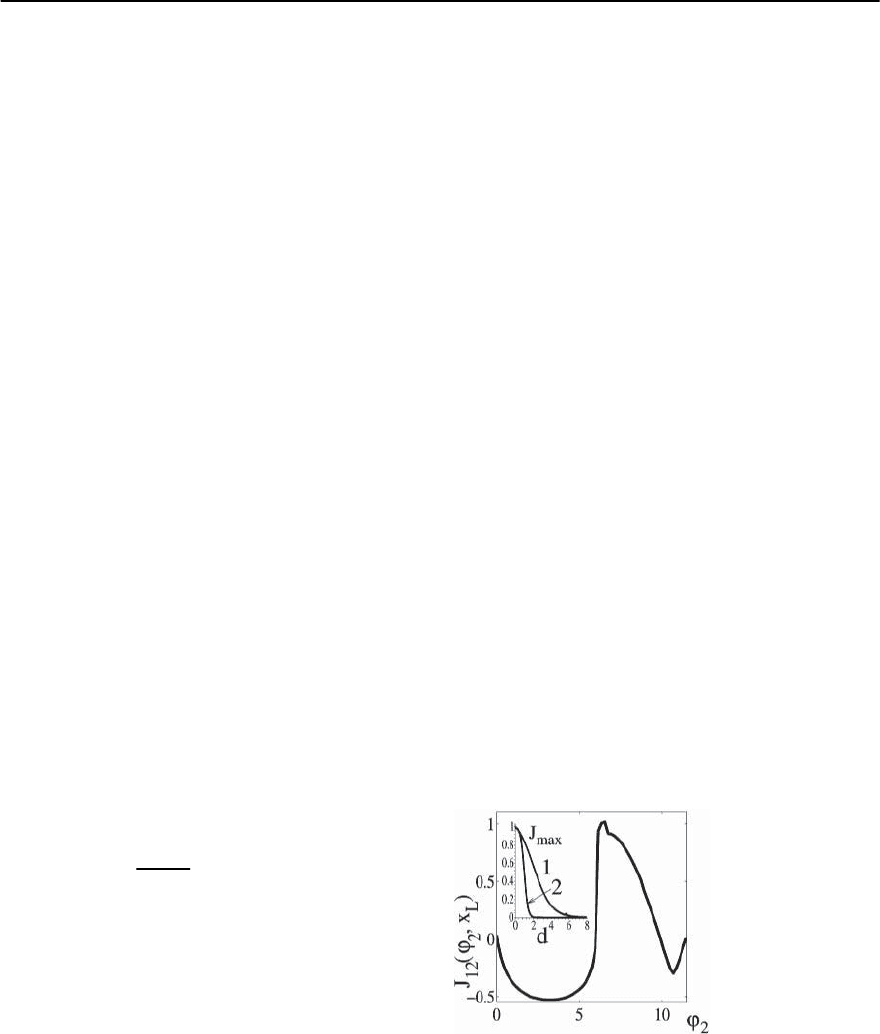
Fig. 9.42. (a)Thetwosubjunctions.(b)TwoSISjunctions

coupled capacitively. The dashed line with a cross indi-

cates that the coupling is not phase coherent (see Fig. 9.40).

titerminal junction

Though the two electrodes are separated,they couple

via the superﬂuid condensate. Following [91,99] we

quote this process as a non-local Andreev reﬂection

(NA). The NA process is actually equivalent to in-

jecting of two spin-entangled electrons, which form

a singlet state of a Cooper pair spread between two

different leads . The NA was studied experimentally

in [99] using a double-barrier three-terminal NISIN

junction. Similar double-barrier three-terminal SI-

NIS devices were recently examined also in [92]. The

quantized oscillation spectrum of a highly transpar-

ent SISIS junction was studied in [91]. The coherent

interaction through the double-barrier junction is

noticeable even if the barrier transparency is rela-

tively low (i.e., D ≈ 10

−5

, as in the NISIN structures

used in [99]).Then, quantum coherence (QC) estab-

lished across the whole SISIS junction yields a finite

coupling between the right and the left SIS subjunc-

tions via their common middle S layer.

The QC coupling energy J

between the two sub-

junctions 1 and 2 (see Fig. 9.42) is defined as

)=max

W − W

(0)

, (9.72)

where







SISIS



)d'



(9.73)

is the energy of the whole SISIS junction. The energy

of two single SIS junctions connected in series is

(

)







SISIS



)d'



. (9.74)

The two energies W and W

(0)

are not equal to each

other because the current across the middle elec-

trode of SISIS junction is evidently a phase-coherent

supercurrent,while the electric current between two

single SIS junctions connected in a sequence [as

shown by the dash line with a cross in Fig. 9.41c]

is not phase-coherent. This difference between W

and W

(0)

coming from the phase coherence in SI-

SIS serves as a source of our inter-subjunction cou-

pling. The QC coupling between the left and right

SIS subjunctions may be tuned by attaching a third

terminal to their common S layer.Then the phase dif-

ferences '

and '

across the left and right barriers

of the SISIS junction are controlled independently

from each other and the quantum states of each sub-

junction are addressed individually. Though a mi-

croscopic calculation of J may be performed in vari-

ous ways, here we implement a quasiclassical Green

9 Principles of Josephson-Junction-Based Quantum Computation 353

function method with special boundary conditions

at the interface barriers [90,100–102]. The approach

allows a direct microscopic delineation of the inter-

junction coupling and is applicable to junctionswith

arbitrary interface transparency and pureness of the

electrodes.

TheQCcouplingistunedbythebiassupercur-

rents I

and I

. The bias is applied to each of the SIS

subjunctions individually, as shown in Fig. 9.41. If

= I

, then the corresponding phase differences '

and '

are not equal to each other (i.e., '

= '

while the net supercurrent I



, '

, x



inside the

middle S layer of the SISIS junction depends also on

the coordinate x in the direction perpendicular to

interfaces.

The approach [90,102–104] gives a tractable mi-

croscopic description of the bias-controlled QC ef-

fect in multilayered superconducting junctions.The

basic elementary process responsible for the coher-

ent coupling in the system is the Andreev reﬂection.

In this approach, a moving hole creates a new elec-

tron with a reversed trajectory of motion. Most im-

portant is that the multiple processes of the electron-

hole conversion keep the packet on a classical tra-

jectory in the r-p space. The particles may switch

to another classical trajectory at the knots, where

the scattering occurs with a certain probability de-

scribed by special boundary conditions. The quasi-

classical approximation had proven to be effective

when studying the phase coherent transport in mul-

tilayered superconducting structures [75,95,99].The

non-uniform supercurrent I



, '

, x



is obtained

from the one-point quasiclassical Green function ˆg



, '

, x



ep



−1

dTr

Imˆg (", , '

, '

, x)

(9.75)

where  =cos# , # being the electron incidence an-

gle,p

is the Fermi momentum, 

is the normal elec-

tron density of states at the Fermi level. The Green

function ˆg in Eq. (9.75) is expressed as

ˆg

(

)



−

(

)

(

)



−1



(

)

−

(

)

−

(

)

(

)



(9.76)

where spinors

(

)

are

¯ =−i

ˆ



v −u



, (9.77)

and T means transposing. The electron and hole en-

velope wavefunctions u and v are defined on classi-

cal trajectories. The trajectories are coupled to each

other at the knots,associatedwith the interfacebarri-

ers. The non-uniform supercurrent Eq.(9.75) is used

to control the coupling between the two SIS subjunc-

tions as will be discussed in the next section.

9.5.2 Inter-Qubit Coupling Energy

The inter-qubit coupling energy J

is computed us-

ing Eqs. (9.75), (9.76); see Fig. 9.43. The microscopic

equations (9.75), (9.76) describe the properties of

junctionswith arbitrary transparency.They allowac-

counting for the tunneling across the interface barri-

ers I, for the elastic electron scattering on atomic im-

purities, and for the inelastic scattering on phonons

in the junction’s electrodes.As a first step toward the

computing J

we solve the quasiclassical Andreev

equation

= E

(9.78)

for ¦

(x)and¦

−

(x). The equation is completed by

special boundary conditions [96–99] at the interface

barrier positions x = x

L(R)

,andatx = ±∞ for the

geometry of Fig. 9.41. The solution serves as a plug

into Eq. (9.76) for the quasiclassical retarded Green

function ˆg

(

)

. Substituting ˆg

(

)

into Eq. (9.75) one

computes the total supercurrent I



, '

, x



.The

Fig. 9.43. The QC coupling energy of the left SIS subjunc-

tion.The inset shows the maximum coupling strength J

max

versusthethicknessofthemiddlelayerfor“clean”(curve 1)

and “dirty” limits (curve 2)

354 S.E. Shafranjuk and J.B. Ketterson

local current-phase relationships obtained for I

in-

side the middle layer of the SISIS junction are shown

in Fig. 9.42c where I

is denoted as I





for fixed

= /4 at the left barrier x = x

,asI

(0)





at the

middle of the junction x =0,andasI





at the

rightbarrierx = x

.Hereweassumethat'



1, 2

= '

1, 2

Then the local supercurrent I

(

)

depends upon two

phase differences '

and '

, therefore, one may de-

fine a criticalsupercurrent in respect just to one vari-

able(e.g.,'

),and consider its dependence versus an-

other variable (i.e., '

). This behavior is interpreted

as the QC coupling between the two SIS subjunctions

of a symmetric SISIS junction characterized by an

energy J('

, '

). The coupling energy of the left SIS

subjunction, which depends also on the phase differ-

ence across the right SIS subjunction '

is obtained

from Eq. (9.72). In Eq. (9.72)



, '



2

−



, '



−



, '



(9.79)

is the SISIS “washboard” Josephson energy. In

Eq.(9.79), I

is the absolute (i.e., in respect to both '

and '

) critical current of the SISIS junction while

the Josephson energy of the coupled SIS subjunction

1(2) is defined as

(

)



, '



2

(

)



−∞

, '

, x

)d'

(

)

. (9.80)

Equation (9.72) completed by Eqs. (9.75), (9.76),

(9.79),and (9.80) constitutesthe QC coupling J

)

of the left SIS subjunction to the right SIS subjunc-

tion versus '

and '

, tuned by corresponding bias

supercurrents I

and I

(assuming here that '



= '

and '



= '

). We emphasize that the coupling J

comes entirely from the phase coherence between

the two SIS subjunctions.

The computed dependence J

)atx = x

plotted in Fig. 9.43, from which one can see that

the sign and magnitude of J

) is controlled by

the phase difference '

across the counterpart SIS

subjunction. The QC coupling magnitude J(d)=

max

)} (d is the middle layer thickness in

units of the BCS coherence length) is plotted in in-

set to Fig. 9.43, which shows how J depends on the

thickness and purity of the middle layer character-

ized by the electron elastic mean free path l

:ifitis

very thick (d  ), the mutual interaction of sub-

junctions J vanishes. When the electron motion in-

side the middle layer is ballistic (l

≥ ),the SIS sub-

junctions interact with each other though the middle

layer is relatively thick (curve 1 in Fig. 9.43 for which

=5). If, however, the middle layer is impure, the

coupling range shortens: ∗

∼



l

, which is con-

firmed by our numerical calculations of J (see curve

2 in Fig. 9.43 computed for l

=0.3). This circum-

stance can be utilized to optimize the coupling in

two-qubit gates.

9.5.3 Control of the Inter-qubitCoupling

In the setup shown in Fig. 9.41, the two SIS sub-

junctions are used as two coherently coupled qubits.

The two-qubit idle state | ¥

1,2

is realized when the

strength J

of the inter-qubit coupling vanishes at

some value of '

. The manipulations with quantum

states and the inter-qubit coupling are controlled by

applying bias voltages and supercurrents between

the S electrodes.An additional independent control is

furnished when '



= '

and '



= '

(see Fig. 9.41)

as will be discussed in next section. In this section

we analyze basic two qubit gate parameters (i.e., the

level splitting " and the inter-qubitcoupling strength

J) semi-qualitatively. We give a simple illustration to

our description using approximate formulas. Prop-

erties of each individual SIS qubit either 1 or 2 are

conveniently described as a motion of a particle with

the mass C

1(2)

in the “tilted washboard”potential

1(2)

= W

(

)

−

2

1(2)

. (9.81)

The motion inside the quantum well leads to quan-

tized states as sketched in the upper part of Fig. 9.41.

The Josephson energy W

1(2)

of an SIS subjunction

1(2) entering Eq. (9.81) is given by Eq. (9.80). The

subjunction 1(2) is coupled to its counterpart sub-

junction 2(1).

The quantum eigenstates and eigenvalues of the

system in the potential U

1(2)

are obtained numeri-

cally for given geometry of the double barrier junc-

tion. The input parameters for numeric computa-

tions include the capacitances C

1,2

of the left (right)

9 Principles of Josephson-Junction-Based Quantum Computation 355

SIS subjunctions, the S layer thickness d

,thebar-

rier transparency D, the junction area A, the energy

gap , the elastic electron-impurity scattering rate



, and the control supercurrents I

1,2

.Theinter-level

spacing "

(l)

= "

(l)

− "

(l)

is tuned by altering I

.Typi-

cally, one sets the JE profiles to exploit just two lev-

els in each quantum well, while the third level (used

for the readout of the quantum state) is positioned

just below the top of the well (see the upper part

of Fig. 9.41), which is achieved in large area junc-

tions when I

/2  e

/2C and I

− I

1, 2

 I

.In

this approximation, the SISIS junction behaves like a

non-relativistic two-bodysystem.Then the wholebe-

havior of the SISIS gate is reduced to a trivial motion

ofthecenterofmass.Therelativeone-bodymotion

is executed by a particle of mass C = C

/(C

+ C

)

(where C

and C

are the capacitances of the left and

right SIS subjunctions). The motion is described by

a “coordinate” = '

− '

about a fixed center un-

der the action of an “elastic force”F



=−@U ()/@.

Here we are interested in a relative motion of the

reduced “mass” C in the two-well model potential

(



)

shown in Fig. 9.44. Simple analytical formulas

are obtained when the two-well U

(



)

is further ap-

proximated by a function pieced together from two

qubic parabolas. Each of the qubic parabolas has a

quadratic curvature at the bottom,which gives a clas-

sical oscillation frequency

1/4



2I



1−



1/4

(9.82)

controlled by the supercurrent I

The two characteristic barriers in the model po-

tential U() have the height

U

√

3



1−



3/2

, (9.83)

where l is related to the left (l =1)andright(l =2)

wells. The two wells are separated by a hump, which

in a symmetric case has the height U

∼



/2,

where 

is the distance between the two wells (see

Fig. 9.44).

Although the applicability of such an approxi-

mation is limited, it serves as a good illustration

when modeling qubit switches. Generally speaking,

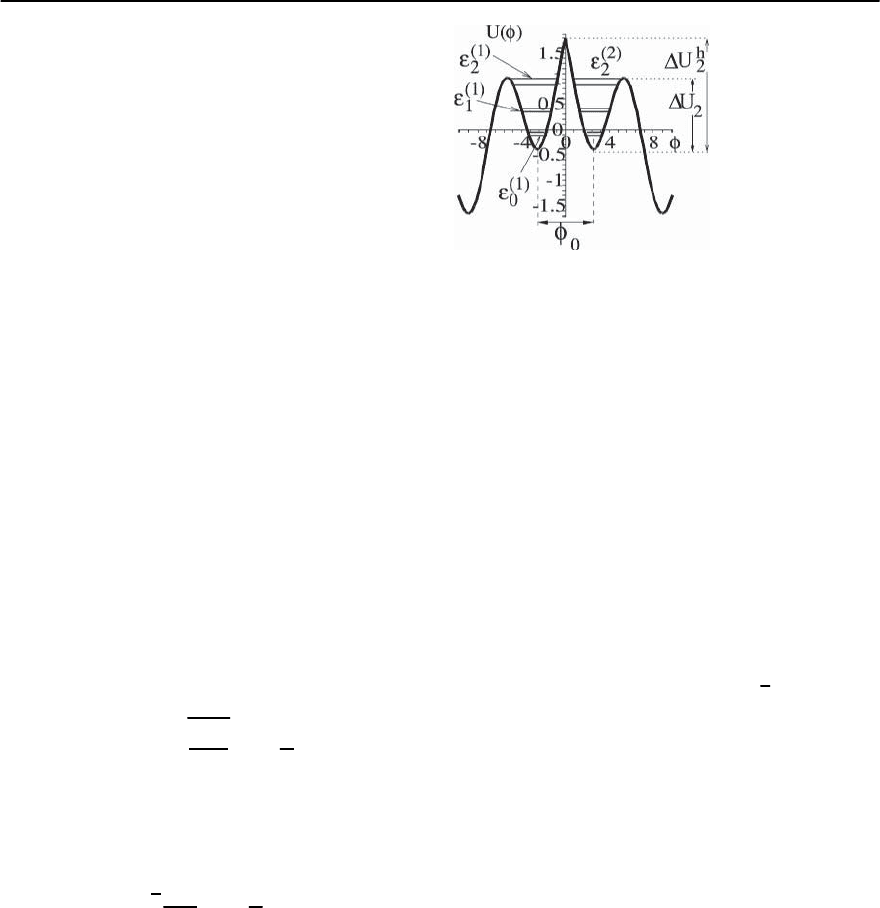
Fig. 9.44. A two-qubit gate potential with two wells sepa-

rated by a hump, which is controlled by the bias supercur-

rents I

and I

.Thequantized levels "

(l) are formed in each

of the wells,while the interlevel splitting "

is controlled by

the hump height

the energy spacing "

(l)

= "

(l)

− "

(l)

and the tun-

neling matrix element , which enter Hamiltonian

(9.71), depend on the reduced phase difference  in

quite a complicated way.A finite inter-qubitcoupling

J = 0 splits each level additionally, i.e., "

(

)

→ "

(

)

(n =0...3andl =1, 2 ), so the relevant splitting

magnitude is ı"

(

)

= "

(

)

− "

(

)

−

.Inthelimitofa

weak inter-qubitcoupling,fora symmetrictwo-qubit

gate,within our two-body motion model oneapprox-

imately finds [101,102]:

= P

−



" + 



/3 ,

1, 2

= E

=−P

−

/2+



" + 



/3 ∓ i

√

(9.84)

and

ı"

(

)

=2!

(

 /

)

1/2

exp

(

−

)

, (9.85)

where  = C!



/, and the quantized level ener-

gies of a non-interacting qubit are

= "

+ !



1−

(

5/36

)



!

/U



(9.86)

and

= "

+ !



1−

(

11/36

)



!

/U



. (9.87)

In the above formulas we omitted the qubit index l

for brevity.

9.5.4 Additional Control by Transport Supercurrents

The two-qubit quantum state | ¥

1,2

is controlled by

two bias supercurrents I

and I

as shown in Fig.9.41.

356 S.E. Shafranjuk and J.B. Ketterson

By changing the magnitude and direction of both I

and I

one shifts the quantized level positions "

(

)

and their splitting ı"

(

)

.However the two parameters

and I

are generally not enough for a full control

of the two-qubit gate. In addition to the manipulat-

ing with each individual qubit one must tune the

inter-qubit coupling as well. This requires three in-

dependent control parameters at least.An additional

independent control over the two-qubit gate is ac-

complished with applying transport supercurrents

(k =1...3)alongtheSelectrodesasshownin

Fig. 9.45a (see also Fig. 9.41). If the magnitudes of

ıI

= I

− I

and ıI

= I

− I

are finite, the

“washboard”Josephson energy U is modified, which

in turn changes the two-qubit state | ¥

1,2

. When the

SISIS junction in the lateral z-directionis sufficiently

long, i.e., L ≥ 

(where 

= c



8e(2

+ d



is the Josephson penetration depth, 

is the London

penetration depth, d

is the thickness of the insulat-

ing barrier, j

is the Josephson critical supercurrent

density), the distribution of Josephson supercurrent

(z) inside each of the SIS subjunctions becomes

non-uniform [103] and depends also on the lateral

coordinate z. Such an inhomogeneous distribution

of the supercurrent density j

across each of the SIS

subjunctions causes a finite phase change ı'

along

the z-directionproviding that ı'

= '



−'

=0and

ı'

= '



− '

= 0 (see also Fig. 9.41).

This situation resembles the penetration of mag-

netic ﬂux into a long Josephson junction [103]. In

our case ıI

plays a role similar to the y-component

of the external d.c. magnetic field H

, which was the

case in [94,105].Accordingto [102,106],thej

(z)pro-

file depends on the ratio L/

: the supercurrent den-

sity is highly inhomogeneous for large L/

when a

magnetic ﬂux enters the subjunction. Anactual j

(z)

dependence versus ıI

is obtained from the sine-

Gordon equation:



sin '

, (9.88)

completed by the boundary conditions



/@z



z=0

=0and



/@z



z=L

= ıI

/en

= ,

where n

is the superﬂuid charge carrier concentra-

tion [94]. In the BCS approximation one gets

= n







(2k +1)

+ 



−3/2

, (9.89)

n is the normal charge carrier concentration,T is the

temperature,  is the energy gap.

The solution '

(

)

of Eq. (9.88) is given in ellip-

tic functions [90,107]. In Fig. 9.45b we show a typ-

Fig. 9.45. (a) An additional control of the two-qubit

states with transport supercurrents I ﬂowing in the ad-

jacent S layers.(b)A nonuniform distribution of thesu-

percurrent j

(z) versus the lateral coordinatez (in units

of 10

/L) along adjacent S layers. (c) The Josephson

energy potential

9 Principles of Josephson-Junction-Based Quantum Computation 357

ical distribution of the supercurrent j

(

)

along

the left subjunction with L/

=10andıI

=0.

In Fig. 9.45c we plot the Josephson energy profile

, ı'

) in the left quantum well at fixed I

for a

longjunctionwith L/

= 10.OnecanseethattheU

profile depends on ı'

(which actually is ∝ ıI

).The

transport supercurrents I

1,2

renormalize the height

of the characteristic barriers U

1,2

(



)

whichacquire

the dependence on  = ıI

/en

. From Eq. (9.88) at

z  

and   I

/en

one finds

U

1, 2



, 



U

1, 2



,  =0





, 



, (9.90)

where U

1, 2



,  =0



= U

1, 2

(



)

and the renor-

malizing function is



, 



=1+











 +

1−



2







2



(9.91)

and we denoted





= U

(



)

/U

, U

= U

(



)

=0

, 



= @



/@.

For a non-interacting junction 



=1−cos,while

for the subjunctions of the SISIS junction the ex-

pression for 



is more complicated and is obtained

numerically for given S layer thickness d

, barrier

transparency D,junctionareaA,energy gap ,elastic

electron-impurity scattering time 

,andcontrolsu-

percurrents I

1,2

.When finite transport supercurrents

1, 2

= 0 are applied, the levels "

1,2

are shifted versus

. The characteristic barriers U

1,2

[see Eq. (9.90)]

entering Eqs. (9.86), (9.87) for "

1,2

are renormalized

by Z



, 



as follows from Eqs. (9.89), (9.91). In this

way,Eqs.(9.86),(9.87) inconjunctionwithEqs.(9.89),

(9.91) constitute the energy level dispersion versus

the control transport supercurrents I

1,2

.Oursolu-

tion demonstrates that the two-qubitstates | ¥

1,2

are

readily controlled by the transport supercurrents I

1,2

in addition to the bias supercurrents I

1,2

9.5.5 Leakage and Fidelity of the Two-Qubit Gate

The intrinsic inter-qubit coupling in the SISIS gate

is executed via weak Josephson supercurrents,which

switching frequency is relatively low (! ∼ 10

–10

−1

).The supercurrents produce no noise in the junc-

tion [103], thus the coupling is“quiet”. Since there is

no ac electric field in the SISIS junction, the distur-

bance to the surrounding circuit elements is negli-

gible. Therefore, the current and charge noises are

typically very low in the SISIS setup. However, the

supercurrent is generated by an external circuit and

the qubit will be exposed to noises of the circuit. Ad-

ditionally, dissipation in real SISIS gates is possible

due to a tunneling of a quantum state through the

characteristic barriersU

1, 2

() (see Fig. 9.44).Since

the tunneling rate  depends on the barrier height

and width exponentially,the populated upper level "

may in principle contribute to the dissipation, espe-

cially if one biases the system such that the tunneling

rate 

out of |2 is



=("

+ "

−2"

)/2 . (9.92)

The relevant tunneling probability is

(2)





dt . (9.93)

Although the P

(2)

magnitude may be significant, the

tunneling probabilities P

(0)

and P

(1)

out of states |0

and |1 are about 10

and 10

times lower as com-

pared to P

(2)

. The dissipation W

due to a transient

population [105] p

of state |2is estimated as:





dt/ . (9.94)

The last formula means that W

is roughly propor-

tional to p

and to the time of measurement t

.The

dissipation is eliminated by keeping the population

of "

as small as possible, and t

as short as possi-

ble during the quantum logic operations [105].

More essential in SISIS qubit gate is an intrinsic

source of errors. Such errors come up when the in-

teraction is turned on (J =0)andarecausedbythe

quan tum leakage. The leakage is taking place if the

Hilbert space of the real gate is larger than the qubit’s

computational subspace. A different time evolution

in the real space and in the computational subspace

causes an error in the gate operation.An ideal unitary

gate operation U

(

)

is obtained when turningon the

inter-qubitcoupling for a time t

.Bychoosingt

one

may accomplish an arbitrary gate operation [3].

358 S.E. Shafranjuk and J.B. Ketterson

The output of an operation is related to the input

stateviathemap¢U

(t)¢,whereU

(t)istheuni-

tary operator which acts on the full Hilbert space,

¢ is the projector to the computational subspace

acting as ¢

H¢ =(|00| + |11|)

H(|00| + |11|),

where |00| =(

1−

)/2, |11| =(

1+

)/2,

|01| =(

−i

)/2,and |10| =(

+i

)/2.Theer-

ror of an operation is minimized by setting ¢U

(t)¢

ascloseaspossibletoU

). In general an optimal

operation requires t = t

as all the system eigenval-

ues are modified by states outside the computational

subspace. The fidelity and leakage probabilities are

defined as

F =1−min

{t}

U

(

)

− ¢U

(t)¢ /2 (9.95)

and

(

)

=1−min





†

(t)¢U

(t)





. (9.96)

The norm ... of an arbitrary operator K is defined

K =Sup



K| 



=Sup





†



(9.97)

over the vectors

| :  |  =1

of the computa-

tional subspace. This definition implies that K =

√



,where

is the largest eigenvalue of K

†

K.The

evolution operator is

(t)=



−ie

|¥

¥

(we set here  = 1). For simple three-state analyses

one uses that

|0 =

⎛

⎝

⎞

⎠

; |1 =

⎛

⎝

⎞

⎠

. (9.98)

and that the eigenfunctions | ¥

 of the Josephson

energy potential of a non-interactive SIS junction at

1,2

= 0 are expressed in terms of Mathieu functions.

So, the evolution in the computational subspace for

atimeintervalt is:

¢U

(t)¢ =



−ie

¢|¥

¥

|¢



−ie

|00| + |11|•|¥



×¥

|(|00| + |11|)

The above Eqs. (9.95)–(9.98) allow modeling of the

basic two qubit characteristics and simulation of the

two qubitgate dynamics with qubitparameters com-

puted in the former sections.According to Eq.(9.98),

basic parameters include the qubit energy level posi-

tions "

0,1,2

, the inter-level tunneling matrix element

 and the inter-qubit coupling energy J

.Major

two-qubitgate characteristics,which are determined

by the inter-qubit coupling and readout, are studied

within the 3 ×3 state analysis. In that case one works

with the 6-dimensional Hilbert space of the real gate,

which includes 3 states | 0

, | 1

,and| 2

for each

of the qubits n =1, 2 affected by the interaction J.

The computation is done in a straightforward way,

using computer algebra and numeric methods. In

this way one begins with microscopic computation

of all the two-qubit parameters for given SISIS ge-

ometry, electrode purity and temperature. The next

stage involves a study of the inter-qubit interaction

J and coupling to external meters. Finally one com-

putes the major dissipative and dynamic properties

of the two-qubit gates, i.e., the leakage and fidelity

described by the Hamiltonian (9.71).

An illustrative insight into the two-qubit dynam-

ics and dissipative characteristics is given by ana-

lytical formulas derived in the former sections. An-

alytical solutions are available for a three-state sin-

gle qubit gate and a 2 × 2-state two-qubit gate. One

may for instance find an analytical expression for a

resonant contribution to the leakage of a three-state

system. The three-state system is described by the

Hamiltonian

⎛

⎝

−" 0

ı"

√

2

√

2ı"+ 

⎞

⎠

→

⎛

⎝

0 E

00E

⎞

⎠

, (9.99)

where the lowest level is positioned at −", ı,and

stand for the matrix elements of inter-level tunneling

with the external field factors included. The arrow in

Eq. (9.99) indicates the diagonalization of H

.The

eigenvectors of (9.99) are: