Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

9 Principles of Josephson-Junction-Based Quantum Computation 329
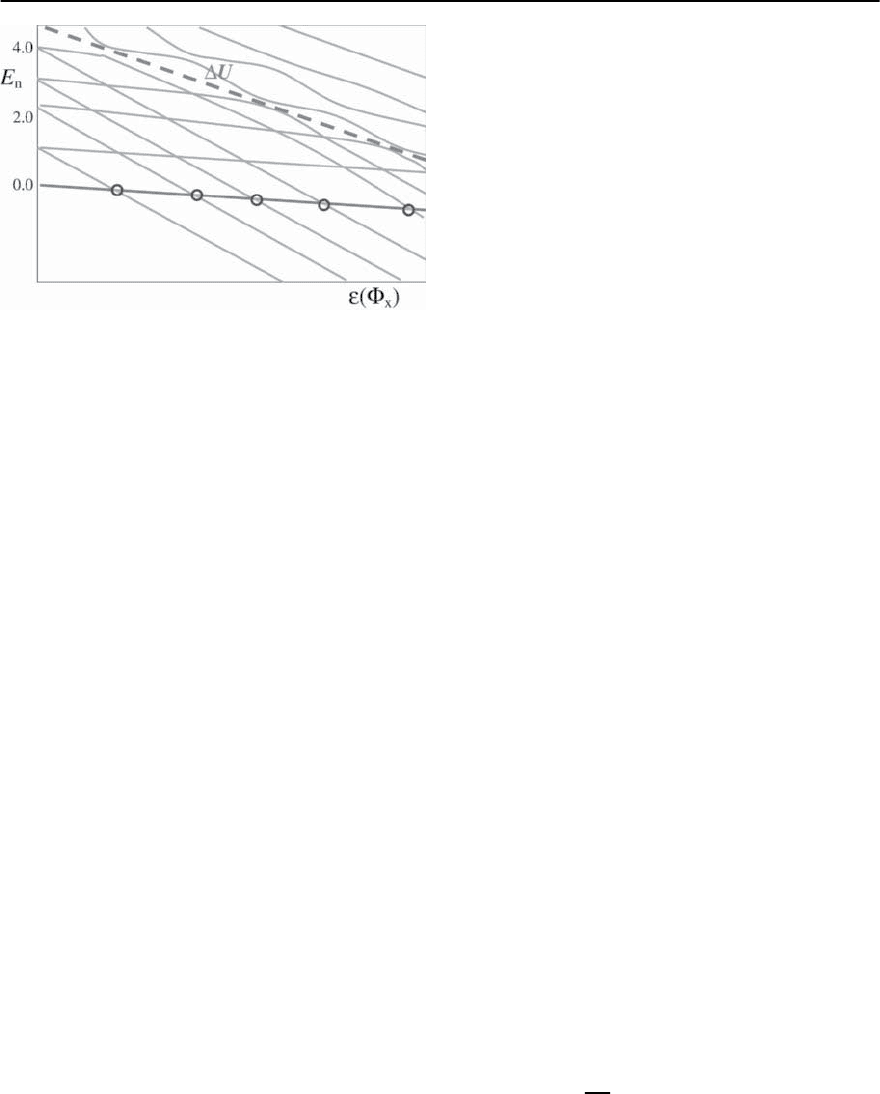
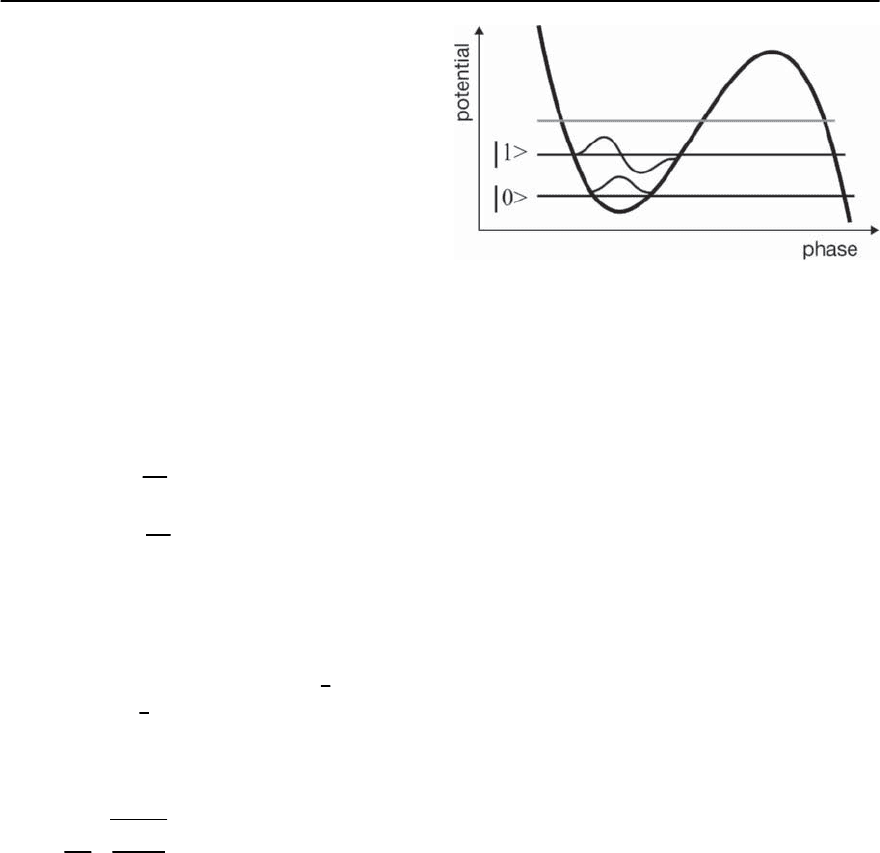
Fig. 9.19. The energy level positions versus the tilt of the
double well potential in a SQUID-type device.The avoided
level crossing is indicated by the dashed line
states typically create a magnetic flux ∼ 10
−3
¥
0
so-
called “persistent current (PC) states”. These states
obey all of the five requirements for a quantum bit:
(1) they can readily be prepared in the ground state
(at a sufficiently low temperature); (2) they can be
precisely manipulated with magnetic fields; (3) two
qubits can be coupled inductively, and that coupling
can be switched on and off; (4) the flux associated
with the PC states can be measured using a SQUID-
type detector; and (5), the states can be made insen-
sitive to background charges and effectively decou-
pled from their electrostatic environment (in con-
trast with charge quantum states in Josephson cir-
cuits); the magnetic couplingto the environment can
also be effectively suppressed.
Another important quantum effect has been re-
ported recently: The groups at Stony Brook [54] and
Delft [55] have experimentally observed the avoided
level crossing due to coherent tunneling of the flux
in a double-well potential. In principle, all other ma-
nipulations discussed in the previous section should
be possible with Josephson flux devices as well. The
group at Stony Brook probed, spectroscopically, the
superposition of excited states in different wells.The
experimental results are shown in Fig. 9.19 for an
r.f. SQUID with a self-inductance L = 240 pH and
ˇ
L
=2.33. In the experiment a substantial separation
of the minima of the double-well potential (of order
¥
0
) and a high inter-well barrier made the tunnel
coupling between the lowest states in the wells neg-
ligible. However, both wells contain a set of higher
localized levels (under suitable conditions one state
in each well) with relative energies that are also con-
trolled by ¥
x
and
˜
¥
x
. Because they were closer to the
top of the barrier, these states mixed more strongly
and formed eigenstates, which were superpositions
of localized flux states from different wells. External
microwave radiation was then used to pump the sys-
tem from a well-localized lowest state in one well
to one of these eigenstates. The energy spectrum
of these levels was studied for different biases ¥
x
,
˜
¥
x
, and the properties of the model associated with
Eq. (9.28) were confirmed. In particular, the level
splitting at the degeneracy point indicated a super-
position of distinct quantum states. They differed in
a macroscopic way: the authors estimated that the
parameters associated with the two superimposed
flux states differed by a flux ¥
0
/4, a current of 2–3
mA, and a magnetic moment of 10
10
B
.
9.3 Qubit Dynamics
In this section we begin by discussing the manipula-
tion of single qubit devices by an external time de-
pendent field. In realistic mesoscopic systems, there
are usually several discrete energy levels (e.g. the
three levels utilized in a phase qubit). However a
qubit utilizes only two of these levels and therefore
care must be taken to isolate these levels from the re-
maining levels. Assuming for the moment that this is
the case, we first review the quantum mechanics as-
sociated with transitions within a two-level system,
which is fundamental to the operation of all qubits.
9.3.1 Transitions Within Two-Level Systems;
the Rabi Frequency
Assume we are given a system with discrete levels
E
n
and states ¥ (q, t)(whereq denotes all spatial
coordinates) that is perturbed by an external time-
dependent field,
ˆ
V(t). We seek an approximate solu-
tion to the time-dependent Schr¨odinger equation,
i
@¦
@t
=
ˆ
H
0
+
ˆ
V(t)
¦ , (9.30)

330 S.E. Shafranjuk and J.B. Ketterson
by expanding in terms of the stationary states, ¦
0
k
,of
the unperturbed system in the form
¦ =
k
a
k
(t)¦
0
k
, (9.31)
where, as indicated, the coefficients a
k
(t)aretime-
dependent. Substituting (9.31) in (9.30),and keeping
in mind that
i
@¦
0
k
@t
=
ˆ
H
0
¦
0
k
, (9.32)
one gets
i
k
¦
0
k
@a
k
@t
=
k
a
k
ˆ
V
(
t
)
¦
0
k
. (9.33)
After multiplying both sides of (9.33) by ¦
0∗
m
and in-
tegrating over configuration space one finds
i
@a
m
@t
=
k
ˆ
V
mk
a
k
, (9.34)
where
V
mk
(
t
)
=
¦
0∗
m
ˆ
V¦
0
k
dq = V
mk
e
i!
mk
t
, !
mk
=
E
0
m
− E
0
k
.
(9.35)
In a two-level qubit one normally uses a weak peri-
odic perturbation of the form
ˆ
V =
ˆ
Fe
−i!t
+
ˆ
F
†
e
i!t
(9.36)
which yields
V
kn
(
t
)
= V
kn
e
i!
kn
t
= F
kn
e
i
(
!
kn
−!
)
t
+ F
∗
nk
e
i
(
!
kn
+!
)
t
.
(9.37)
The external field frequency is selected to satisfy
E
0
m
− E
0
n
=
(
! + "
)
, (9.38)
where " is a small detuning frequency. Near reso-
nance, one of the coefficients in the expansion (9.31)
becomes large since the essential contributioncomes
from terms for which !
mn
−! is small.One then ob-
tains the following system of equations
i
@a
m
@t
= F
mn
e
i
(
!
mn
−!
)
t
a
n
= F
mn
e
i"t
a
n
(9.39)
i
@a
n
@t
= F
∗
mn
e
−i"t
a
m
. (9.40)
Substituting
a
n
e
i"t
= b
n
(9.41)
we obtain the pair of equations
i ˙a
m
= F
mn
b
n
, i
˙
b
n
− i"b
n
˙a
m
= F
∗
mn
a
m
(9.42)
which give
¨
b
n
− i"
˙
b
n
+
1
2
|F
mn
|
2
b
n
=0. (9.43)
The two independent solutions of this equation are
chosen as
a
n
= Ae
i˛
1
t
, a
m
=−A
˛
1
F
∗
mn
e
i˛
2
t
, (9.44)
a
n
= Be
−i˛
2
t
, a
m
=−B
˛
2
F
∗
mn
e
i˛
1
t
, (9.45)
where A and B are integration constants (being de-
termined from initial conditions) and
˛
1
=−
"
2
+ § , ˛
2
=
"
2
+ § ,
§ =
7
"
2
4
+
2
, =
F
mn
,
(9.46)
where is the so-called Rabi frequency,whichdeter-
mines the rate at which the system cycles between the
states. Hence the perturbation transforms the wave
functions of a quantum mechanical two-level system
as
¦
0
m
, ¦
0
n
→ a
n
¦
0
n
+ a
m
¦
0
m
; (9.47)
i.e., it mixes the initial unperturbed states in a deter-
ministic manner.
A two-level system can be used to implement a
quantum bit provided it can be manipulated,projec-
tively readout, and coupled to similar devices in a
controlled way. But such systems, in practice, always
couple to the external environment at some level,
and that introduces a loss of coherence on a time
scale characterized by a coherence time.Thenum-
ber of single-qubit operations that can be conducted
during a coherence time is then a measure of the

9 Principles of Josephson-Junction-Based Quantum Computation 331
qubit performance. The coherence time is limited
by interactions with the other degrees of freedom
in the environment, including the manipulation and
readout systems.Achieving full control and long co-
herence times in a qubit are somewhat incompatible
goals; strong coupling is desirable when preparing a
state; in addition, readout requires strong coupling
to another physical system which is measured at the
macroscopic level. On the other hand, a high degree
of isolation is required as the prepared state evolves.
Although most qubit devices have their own unique
features, their coupling to the environment can often
be described in a generic way, which we now discuss.
9.3.2 Manipulation, Readout and Decoherence
We start by considering the effect on a qubit circuit
of a term in the Hamiltonian
ˆ
H
c
=
ˆ
X that cou-
ples a qubit variable
ˆ
X to an external variable. The
coupling entangles the qubit with the environment,
thereby introducing decoherence. The readout gives
the expectation value of
ˆ
X, and the measured signal
is X
01
=
1
ˆ
X
1
−
0
ˆ
X
0
.Thissignalisdirectly
related to variations of the qubit transition energy
!
01
(or frequency !
01
) with the average value of
the external variable treated as a control parame-
ter:
X
01
=
@(!
01
)
@
. (9.48)
When the coupling is weak, the decoherence is min-
imal and does not modify the qubit states; the
qubit will then be projected onto an eigenstate on a
time scale determined by a characteristic coherence
time [56–59].
Decoherencecan be describedin terms of two pro-
cesses: relaxation processes, in which an energy !
01
is exchanged between the qubit and its environment,
and dephasing processes,in which the relative phase
between the two qubit states grows randomly with
time. The latter, which formally represents an en-
tanglement between the qubit and its environment,
is characterized as arising from a modulation of the
qubittransitionfrequency caused by the fluctuations
of the control variable, measured by .
2
The random
phase-shift accumulatedbetween the two qubit states
in a time t is then given by
ı' =
t
0
@!
01
@
ı
t
dt
. (9.49)
To characterize ı
(
t
)
one introduces a fluctuation
spectrum, S
(!). This spectrum is usually modeled
as being constant below a characteristic cut-off fre-
quency !
C
, but for times longer than !
−1
C
,theco-
herence factor,
9
exp(iı')
:
, decays exponentially; the
characteristic time is given by [60,61]
T
'
=
2
@!
01
@
2
S
(! =0)
. (9.50)
In general, the spectral density S
(0) is the sum of
contributionsarising from many sources: 1) thermal
fluctuations of the environment (which are propor-
tional to temperature), 2) non-equilibrium excess-
noise arising from uncontrolled variables (e.g. sub-
strate charge fluctuations in charge qubits), and 3)
the readout system (e.g. noise arriving from in-
put/output leads).
3
On comparing (9.48) and (9.50) it is clear that the
dephasing time T
'
and the measured signal X
01
are
closely interrelated.In addition,coupling the qubitto
a readout system can introduce extra noise over that
required by the measurement process itself, which in
many cases cannot be avoided. However by working
at a stationary point where @!
01
/@ =0,longde-
phasing timescan still beachievedsince this will sup-
press the coupling to all noise sources to first order.
At such a point we have X
01
=0;hence must be
shifted prior to readout.Below we will discuss a read-
out strategy for a qubit circuit based on the Cooper
pair box(where quantum coherence hasalready been
demonstrated).In this so-called quantronium device,
activating the readout automatically drives the qubit
away from this optimal working point [62].
2
This semi-classical approximation (which breaks down in the zero-temperature limit) is applicable to Josephson
junction based qubits studied to date.
3
A special treatment is required when the spectral density diverges at low frequency (so called 1/f noise).
332 S.E. Shafranjuk and J.B. Ketterson
9.3.3 Phase Qubit Dynamics
The Hamiltonian
The basic ideas underlying the Josephson phase
qubit were discussed in Sect. 9.2.3. Here we discuss
their dynamics in more detail.If we restrict ourselves
to three levels,the Hamiltonian of a biased Josephson
junction is written as
H =
1
2C
Q
2
−
I
0
¥
0
2
cos ' −
I¥
0
2
' , (9.51)
where I is the bias supercurrent,I
0
is the critical cur-
rent, C is the junction capacitance, and ¥
0
is flux
quantum. The operators Q and ' correspond to the
charge and phase difference on the junction. The
above Hamiltonian can be approximated by [63]
H =
⎛
⎝
E
0
00
0 E
1
0
00E
2
⎞
⎠
+
¥
0
2
I
⎡
⎢
⎢
⎣
9
0
'
0
:9
0
'
1
:9
0
'
2
:
9
1
'
0
:9
1
'
1
:9
1
'
2
:
9
2
'
0
:9
2
'
1
:9
2
'
2
:
⎤
⎥
⎥
⎦
.
(9.52)
where I =−I
w
(t)cos(!t + ), ! is the frequency
ofther.f.current,and is the phase shift. Here E
0
, E
1
and E
2
are the energies of the three lowest levels. The
matrix elements
9
m
'
n
:
are calculated as follows.
We assume the presence of a dc current such that we
can approximate the potential as a cubic polynomial.
This Hamiltonian can be diagonalized numerically
in terms of the energies of the three lowest states and
the matrix elements
9
m
'
n
:
computed. Calculating
9
m
'
n
:
in this manner, one obtains
H ≈
⎛
⎜
⎜
⎝
E
0
g
(
t
)
e
i
(
!t+
)
0
g
(
t
)
e
−i
(
!t+
)
E
1
√
2g
(
t
)
e
i
(
!t+
)
0
√
2g
(
t
)
e
−i
(
!t+
)
E
2
⎞
⎟
⎟
⎠
+H
nr
(9.53)
where the basis states are |0, |1,and|2 from left to
right,! is the frequency of the applied time-varying
r.f. current, and g
(
t
)
=1.014I
w
(
t
)
√
/2!
01
C/2is
an “envelope function” related to the time-varying
current, I
w
(t). The numerical coefficient 1.014 has
been obtained from the bias supercurrent magni-
tude. A shaped pulse is generated using the envelope
function, g(t). The remaining contributions to the
Hamiltonian, H
nr
, involve additional diagonal and
non-diagonal elements, all of which are sufficiently
far from the resonances associated with !
10
and !
12
that they can be neglected. One can then perform
operations between the |0 and |1states while min-
imizing those between |1 and |2.
The Rotating Frame
To calculate the effect of the envelope function it is
convenient to move into a doubly rotating frame,de-
fined by the unitary operator
ˆ
V(t)=
⎛
⎜
⎜
⎝
10 0
0 e
i!t
0
00 e
2i!t
⎞
⎟
⎟
⎠
. (9.54)
Let | =
ˆ
V
:
be a state in the rotating frame gen-
erated by
ˆ
V where
:
is a state in the laboratory
frame. The equation of motion for | canthenbe
derived from the Schr¨odinger equation, and has the
Schr¨odinger-like form
i
@
@t
| =
˜
H | , (9.55)
where
˜
H is the rotating frame Hamiltonian given by
˜
H = V
†
HV − iV
†
(
@V /@t
)
and is given by
˜
H =
⎛
⎜
⎜
⎝
0 g
(
t
)
e
i
0
g
(
t
)
e
−i
E
1
− !
√
2g
(
t
)
e
i
0
√
2g
(
t
)
e
−i
E
2
−2!
⎞
⎟
⎟
⎠
, (9.56)
wherewehavesetE
0
= 0.We will limit ourselves here
to on-resonance excitation involving the |0↔|1
transition. Using E
1
= !
10
, !=!
10
, and defining
the energy difference between the two transitions as
E
2
−2E
1
= ı
!
, Eq. (9.56) becomes
H =
⎛
⎜
⎜
⎝
0 g
(
t
)
e
i
0
g
(
t
)
e
−i
0
√
2g
(
t
)
e
i
0
√
2g
(
t
)
e
−i
ı
!
⎞
⎟
⎟
⎠
.
(9.57)
This rotating frame Hamiltonian can be used to di-
rectly calculate the effect offlat topped (termed hard)

9 Principles of Josephson-Junction-Based Quantum Computation 333
pulses.“Shaped”pulses can be treated by discretizing
anassumedform for g(t) as a series of steps,g
j
,acting
fortimes,t.Duringthej
th
slice,U
j
=exp(−i
˜
H
j
t/)
and by multiplying a succession of these forms we
obtain the total evolution as
U =
A
j
U
j
=
A
j
exp (9.58)
×
⎡
⎢
⎣
−
it
⎛
⎜
⎜
⎝
0 g
j
e
i
0
g
j
e
−i
0
√
2g
j
e
i
0
√
2g
j
e
i
ı
!
⎞
⎟
⎟
⎠
⎤
⎥
⎦
.
From U we can calculate the“leakage”out of the two-
level qubit manifold. From Eq. (9.58) we see that the
effects of ı
!
scale as tı
!
/2;anappropriatetime
unit is therefore
pw
= tı
!
/2, and the results given
below are plotted in terms of this parameter.
Shaped and Comp osite Pulses
Shaped pulses are widely used in NMR quantum
computing since they can significantly enhance the
selective excitation of a qubit compared with hard
pulses. In contrast to NMR, where each qubit is rep-
resented by a spin-1/2 particle, the two transitions in
our phase qubit share the same potential well, lead-
ing to a more complex dynamics. Although it is not
immediately obvious that pulse shaping can be use-
ful, detailed calculations [63] (see below) show that
some benefit is possible. Here we will limit ourselves
to a 180
◦
rotation (a pulse in NMR jargon) which
involves the |0↔|1 and |1↔|0 transitions,
since it is usually most difficult to selectively carry
out this rotation. Calculations have been performed
for several pulse shapes including Gaussian and the
so-called Hermite forms. The r.f. envelope, g(t), for
the Gaussian is given by
g
gauss
(
t
)
=
a/t
g
exp
−t
2
/2t
2
g
; (9.59)
here t
g
is the characteristic pulse width and a is the
pulse amplitude. This form can be “truncated” by
setting g(t) = 0 for |t| > ˛t
g
,where˛ is a cutoff pa-
rameter (usually 3 to 5); the total pulse width t
pw
is
then 2˛t
g
. For 180
◦
pulses a ≈ 1.25 (for typical val-
ues of ˛ The Hermite shape is defined as a Gaussian
multiplied by a second order polynomial
g
hrm
(
t
)
=
1−ˇ
t/˛t
g
2
a/t
g
×exp
−t
2
/2t
2
g
,
(9.60)
where ˇ determines how strongly the Gaussian pulse
is modulated and the remaining parameters are the
same as above. For ˇ = 4 and a 180
◦
rotation angle,
a ≈ 2.2 for ˛ =3anda ≈ 1.67 for ˛ = 3. The per-
formance of various pulses has been calculated using
these parameters [63].
An error measure can be defined as " =1−
|U
(
3, 3
)
|
2
where U(3, 3) denotes the (3,3) element
of the resulting unitary transform; " is equivalent to
the probability of the system being in the state |2
after the application of the pulse, when starting from
an arbitrary superposition of the form a |0 + b |1.
Ideally, the error measure vanishes (" =0)ifoper-
ation is confined to the |0, |1 subspace. The mea-
sure " serves as a lower bound.Ofcourse,therota-
tion may deviate slightly from an ideal rotation even
when " = 0. One also has to account for the so-called
transient Bloch-Siegertshifts,similarto thoseseen in
NMR; however these effects can be corrected using a
method similar to the one described in [64].
One can calculate " numerically using Eq. (9.58),
however to gain an intuitive understanding of the
utility of a given envelope function one can use a
simple bandwidth argument.Given that the response
is approximately linear for small rotation angles, one
canFouriertransformagivenenvelopefunction;this
procedure is extensively used in NMR,even when the
rotation angles are large. For an untruncated Gaus-
sian pulse, the relative power at a frequency ı
!
from
!
10
is given by
"(
pw
) ≈ exp
−ı
!
t
2
g
=exp
−(
pw/
˛)
2
. (9.61)
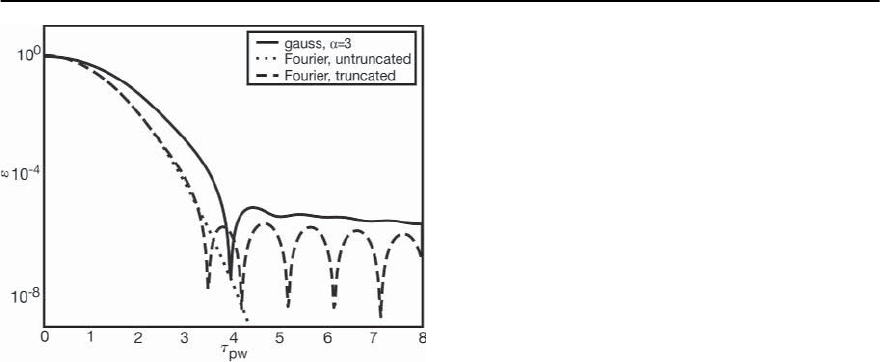
This form is plotted in Fig. 9.20 along with that for
a truncated Gaussian pulse and the exact calculation
using (9.58). For small pulse widths, the exact calcu-
lation and the one based on Fourier analysis of the
untruncated shape are similar, but the exact calcula-
tion flattens out for
pw
> 4. From this example it is
clear that Fourier analysis gives a rough estimate of
the error, especially when the pulses are truncated.
Fourier transforming tells us immediately that hard
334 S.E. Shafranjuk and J.B. Ketterson
Fig. 9.20. Numerical results for the error " as a function of
normalized pulse width
pw
= tı
!
/2 via Fourier analy-
sis using the untruncated and truncated Gaussian shape,
compared with the exact calculation
pulses are inferior relative to Gaussian or Hermite
shapes. In order to quantify the performance accu-
rately however, one must calculate the error numeri-
cally using Eq. (9.58).
One can also use a “composite pulse” consisting
of a sequence of individual pulses that is designed
to reduce certain types of errors, but possibly at the
expense of a longer total duration. The individual
pulses are typically square wave pulses (as they are
the easiest to generate via r.f. switches), but could
be shaped pulses as well. Such pulses have also been
utilized in NMR. The unitary evolution U of a com-
posite pulse is also calculated via Eq.(9.58),where U
j
are just the evolutions associated with the individual
pulses in the sequence.
Decoherence Studies in Phase Qubits;
Junction Resonances
Thusfarwehaveonlyconsideredtheidealcasewhere
the frequency connecting the two lowest levels of
the three-level system lies far from those connecting
the third, but no sources of decoherence are present.
However, in a real Josephson phase qubit, the quan-
tum state can tunnel through the barrier of the cubic
well,and this process acts as a source of decoherence.
Tunneling has the following consequences. First we
know that the tunneling rate depends exponentially
on the barrier height and width,and hence we expect
the upper level to be most susceptible to tunneling.
When the tunneling rate out of this level is high, it
acts as a significant source of decoherence of the |0,
|1 manifold if the |2 state becomes partially popu-
lated. Therefore it is important to keep the amplitude
of the |2stateassmallaspossibleduringsinglequbit
rotations. As discussed above, shaped and composite
pulses can improve the fidelity of single-qubitopera-
tions, but estimates of the associated rates show that
tunneling can still be the dominant source of deco-
herence; for this reason operating a Josephson phase
qubit with three level is problematic. The decoher-
ence can be reduced by using a four level scheme
(see Fig. 9.21b). For typical junction parameters (e.g.
!
10
/2 ≈ 10 GHz,U/!
p
≈ 4,and ı
!
=0.04!
10
),
the associated pulse widths t
pw
are a few to tens of
nanoseconds. The electronics needed to achieve ac-
curate circuit timings, and simultaneously allow the
application of shaped and composite pulses at these
time scales, is non trivial. Possibly some of the tech-
niques used in NMR spectroscopy can be applied to
superconductor-based qubit systems.
We now discuss some experiments that were de-
signed to specifically address microscopic decoher-
ence mechanisms. One such mechanism, studied by
the authors of [65], is coupling to unwanted elec-
tromagnetic modes. These workers found that deco-
herence arising from coupling to spurious junction
resonances strongly affects the amplitude of the os-
cillations. They proposed a model (to be discussed
below) in which these resonances arise from fluctu-
ations in the tunnel barrier, and related them to pre-
vious measurements of the I–V characteristics and
critical-current 1/f noise. Such resonances appear
to be a major source of decoherence and must there-
fore be minimized if a successful Josephson quantum
computer is to be constructed.
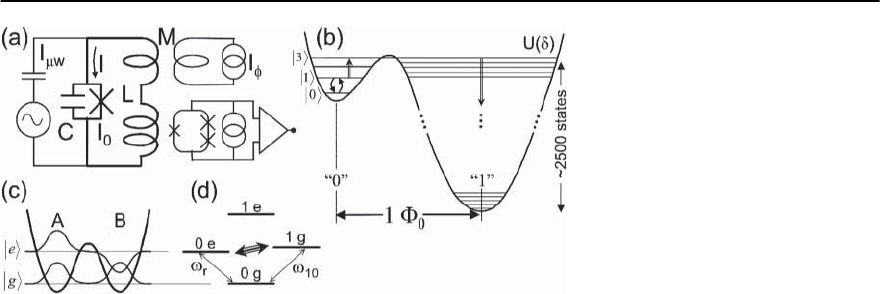
Figure 9.21a shows the circuit used in the ex-
periments. The junction, which is based on an alu-
minum technology, was placed in a superconduct-
ing loop with an inductance L (to minimize quasi-
particle generation and self-heating when the qubit
state is probed); by coupling flux through a trans-
former with a mutual inductance M,thejunction
9 Principles of Josephson-Junction-Based Quantum Computation 335
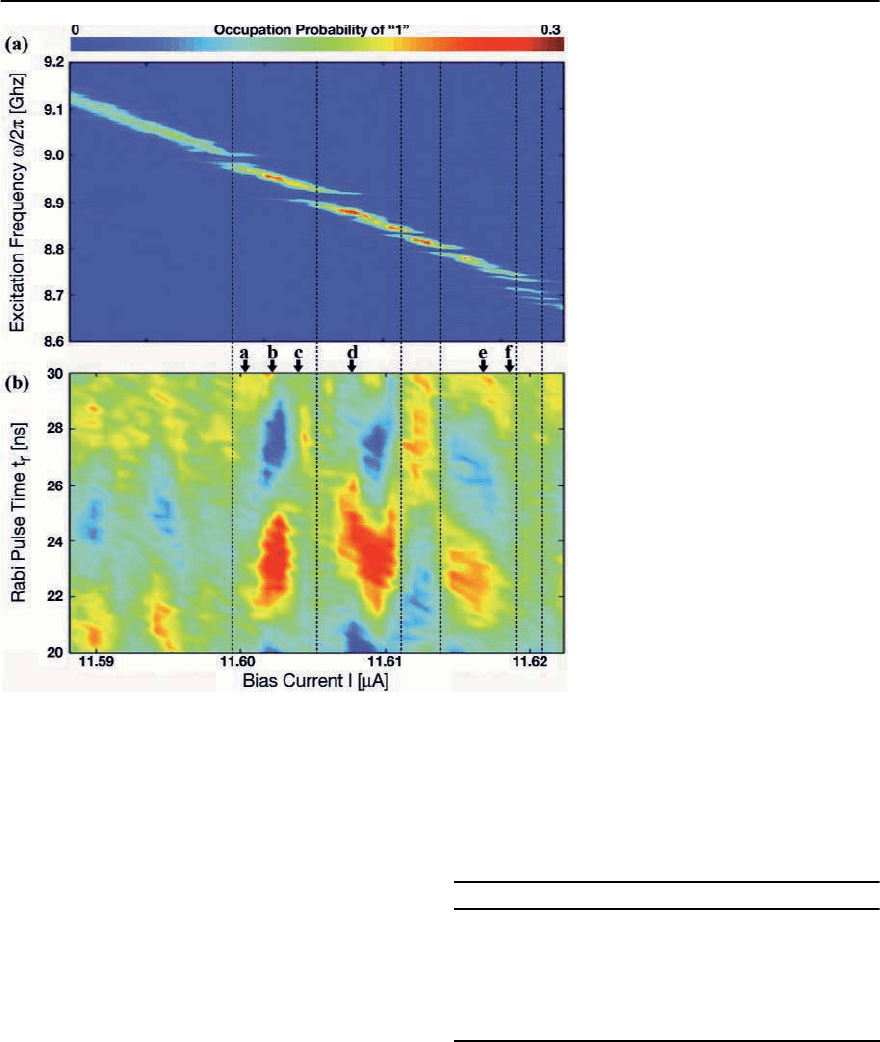
Fig. 9.21. (a) Circuit diagram for the Josephson junction qubit studied by the authors of [65]. Junction current bias I is
set by I
¥
and microwave source I
w
. Parameters are I
0
=11.659A, C = 1.2pF, L = 168pH, and L/M = 81. (b)Potential
energy diagram of qubit, showing a case where there are four levels, |0, |1, |2,and|4, in the cubic well to the left.
Measurement of |1 state is performed by driving the 1 → 3 transition,tunneling to right well, followed by relaxation of
state to bottom of right well.Post-measurement classical states“0”and“1” differ in flux by ¥
0
, which is readily measured
by the readout SQUID. (c) Schematic description of states in a symmetric well.Tunneling between states produces ground
g
:
and excited |e states separated in energy by !
r
.(d) Energy-level diagram for coupled qubit and resonant states for
!
10
≈ !
r
; coupling strength between states
1g
:
and |0e is given by
ˆ
H
int
can be biased close to its critical current I
0
. Unlike
the simple washboard potential discussed in Sect.
9.3.2,the circuitis configured such that there are two
asymmetric wells. With this arrangement the states
in the left well (which can be modeled with a cu-
bic potential) can tunnel into the right well where
(on decaying) they change the flux through the loop
by ∼ ¥
0
=h/2e, which can be read-out with a pulsed
critical-current measurement using an independent
SQUID detector. By applying a microwave current,
I
w
(!), in the presence of a d.c. current-bias pulse,
thevarious transition frequenciescan beprobed.Fig-
ure 9.22a shows the results for the 0 → 1 transition
frequency, !
10
,vs.biascurrent,I
0
; the resonance is
inferred from an increase in the tunneling rate. As
expected, the frequency falls as the bias current in-
creases (and the potential becomes shallower). The
currents used are such that the left well supports ap-
proximately 3–4 energy levels. Note that a number
of small spurious resonances (at the dotted verti-
cal lines in Fig. 9.22) are observed that are charac-
teristic of energy-level repulsion in a coupled two-
statesystem.Thesplittingoftheseextraresonances
is distributed in size; the largest ones are ∼ 25 MHz,
and there is approximately 1 spurious resonance per
∼ 60 MHz.
Rabi oscillations (see Sect. 9.3.1) were observed
between the |0 and |1 states by applying a mi-
crowave pulse at the 0 → 1 transition frequency,
!
10
, for a time t
r
, which is followed by measuring
the occupation probability of state |1 using a sec-
ond microwave pulse resonant at the 1 → 3 tran-
sition frequency, !
31
. Figure 9.23a–c shows the oc-
cupation probability vs. pulse width for three values
of the microwave power; the microwave frequencies
utilized correspond to currents I
0
following from the
spectroscopic studies shown in Fig. 9.22a. The decay
of the oscillations is approximately exponential and
yields a coherence time of 41 ns. The Rabi frequency
vs. microwave amplitude shows the expected linear
behavior, as can be seen in Fig. 9.23d.
Note that strong Rabi oscillations occur only be-
tween the spurious resonances (dashed lines) in
Fig. 9.22b, as is apparent from the coloring; i.e., the
spurious resonances strongly disrupt the Rabi os-
cillations. Figure 9.24 shows the time dependence of
thedecayoftheRabioscillationsforvariousbiascur-
rents ((a) through (f) in Fig. 9.22) in the neighbor-
hood ofthe spurious resonances.Near a spurious res-
onance non-exponential oscillatory decays are ob-
served which appear to involve beating, although the
overall decaytime may remain constant;clearly some
336 S.E. Shafranjuk and J.B. Ketterson
Fig. 9.22. (a) Measured probability of
state “1” versus microwave excitation
frequency !/2 and bias current I for
a fixed microwave power. Data indi-
cate the !
10
transition frequency. Dot-
ted vertical lines are centered at spuri-
ous resonances. (b)Measuredoccupa-
tion probability of the |1 state vs. the
Rabi-pulse time t
r
and bias current I.
In panel (b), a color change from dark
blu e to red corresponds to a probabil-
ity change of 0.4. Color modulation in
atimet
r
(vertical direction) indicates
Rabi oscillations.
kind of mode mixing is occurring. The maximum
amplitude of the Rabi oscillations is approximately
30%, which is significantly less than unity.
The spurious resonances appear to be distributed
randomly,both in size and frequency,and a few small
resonances are likely to be near an arbitrary bias
point. Even for the major resonances, the presence
of several small resonances can still degrade the am-
plitude, thereby reducing the overall amplitude. Spu-
rious resonances have been found in other exper-
iments [68, 69], although the Rabi oscillation data
is usually reported only for the maximum response.
Coherence times and Rabi amplitudes for several ex-
periments are collected in Table 9.1 [65,69]; all the
experiments show some reduction in amplitude.
Table 9.1. Coherence times and Rabi amplitudes observed
in various experiments. All data show a coherence ampli-
tude smaller than unity. Materials for the junction elec-
trodes and barrier are also listed.Values in parentheses are
estimated from published data
Reference Junction Coh. Time Coh. Amp.(%)
[69] Al/AlO
x
/Al 150 ns 50
[65] Al/AlO
x
/Al 1 ‹s (30)
[66] NbAl/AlO
x
/Nb 20 ns (15)
[67] NbN/AlN/NbN 4.9 ‹s(1)
[68] Al/AlO
x
/Al 41 ns 30

9 Principles of Josephson-Junction-Based Quantum Computation 337
Fig. 9.23. (a)–(c) The measured occupation probability of state |1as a function of the Rabi pulse width t
r
for three values
of microwave power, taken at a bias of I =11.609 ‹A (see Fig. 9.22). The microwave power for the responses shown in
(a), (b), and (c) is 0.1, 0.33, and 1.1 mW, respectively. (d) The Rabi oscillation frequency ( in Eq. 9.40) versus microwave
amplitude; the theory predicts a linear dependence
Fig. 9.24. Measured occupation proba-
bility of state |1 versus time duration
of the Rabi pulse t
r
for current biases
a–f as noted by arrows in Fig.9.22.Data
a–e is offset for clarity. Note that when
the bias is changed, the coherence is de-
graded mainly as a loss in amplitude,
not by a decrease in coherence time
338 S.E. Shafranjuk and J.B. Ketterson
Time-Dependent Decoherence
The NIST group [65] also observes that the frequen-
cies and magnitudes of the spurious resonances oc-
casionally change in time, not only when thermally
cycled to room temperature, but even when the de-
vice is cold. The latter strongly implies that at least
some resonances are microscopic in origin, as op-
posed to modes arising from leads to the device or
other sources. These authors constructed a model,
similar to one describing 1/f fluctuationsinthejunc-
tioncriticalcurrent[66,67],involvingtwo-levelstates
within the barrier having large tunneling matrix ele-
ments corresponding to a microwave frequency [67].
Consider two states in the barrier having configu-
rationsA and B that produce criticalcurrents I
0A
and
I
0B
; the interaction Hamiltonian between the reso-
nance and the critical current is then
H
int
=−I
0A
¥
0
2
cos ˆ' ⊗|¦
A
¦
A
|
− I
0B
¥
0
2
cos ˆ' ⊗|¦
B
¦
B
| ,
(9.62)
where ˆ' is an operator corresponding to the
phase difference across the junction, and ¦
A,B
are
wave functions for the two configurations. As-
suming a symmetric potential with energy eigen-
states separated by !
r
,thegroundandexcited
states will be
g
:
=
(
|¦
A
+ |¦
B
)
/
√
2and|e =
(
|¦
A
− |¦
B
)
/
√
2. Using matrix elements for cos ˆ'
appropriate for a phase qubit [70],and including only
the dominant resonant terms arising from this inter-
action Hamiltonian, one has
˜
H
int
=
I
0
2
2!
10
C
×
|01|⊗|e
9
g
+ |10|⊗
g
:
e|
,
(9.63)
where I
0
= I
0A
− I
0B
. Figure 9.25 shows an en-
ergy level diagram for the case where !
r
≈ !
10
.
The coupling of the two intermediate energy lev-
els through
˜
H
int
produces repulsion in the energy
eigenstates. From the magnitude of the level repul-
sions at resonance 2
˜
H
int
/ ≈ 25 MHz,oneobtains
I
0
≈ 65 × 10
−6
I
0
, which is consistent with param-
eters obtained from the current-voltage characteris-
tics.
Fig. 9.25. The energy level diagram in the Josephson junc-
tion potential versus the phase difference
A mesoscopic theory [71] involving a non-
uniform tunnel barrier has been invoked to account
for the Josephson and quasiparticle currents. The
model assumes the current is carried by an ar-
ray of independent tunneling channels. The asso-
ciated transmission coefficients
i
can be obtained
from steps in the quasiparticle current of mag-
nitude 2/
i
that arises from n-th order multiple
Andreev reflections at voltages 2/n [72]. If it is
assumed that the current is carried by only N
ch
channels, then the measured current-voltage char-
acteristics [73] imply a characteristic =4× 10
−3
for a critical-current density of ∼ 40 A/cm
2
.For
the 32 ‹m
2
junction with a normal-state resistance
R
N
=29§ used in the experiments, one obtains
N
ch
= h/2e
2
R
N
=1.3×10
5
,implying a channel den-
sity of 4 ×10
3
/‹m
2
=1/(16 nm)
2
,which in turn im-
plies that N
ch
(I
0
/I
0
) ≈ 8 channels are switched on
andoff between the two junction statesA and B.Since
typical junctionshave a distributionof channels and
the spectroscopy measurement is dominated by the
largest resonances, the magnitude of I
0
likely in-
volves single channels with
i
≈ 2 × 10
−2
.
As noted above the model of these microwave
resonances is similar to that describing 1/f critical-
current noise at audio frequencies.Measurements on
submicrometer Josephson junctions have shown dis-
crete changes in the critical current which are associ-
ated with fluctuatinglinks [66,67,74].A recent exper-
imentonan0.08‹m
2
aluminum junction showed a
change in critical current of I
0
≈ 10
−4
I
0
associated
with a single fluctuator [67].Assuming thislink turns
a channel on and off,the data imply an areal density
