Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

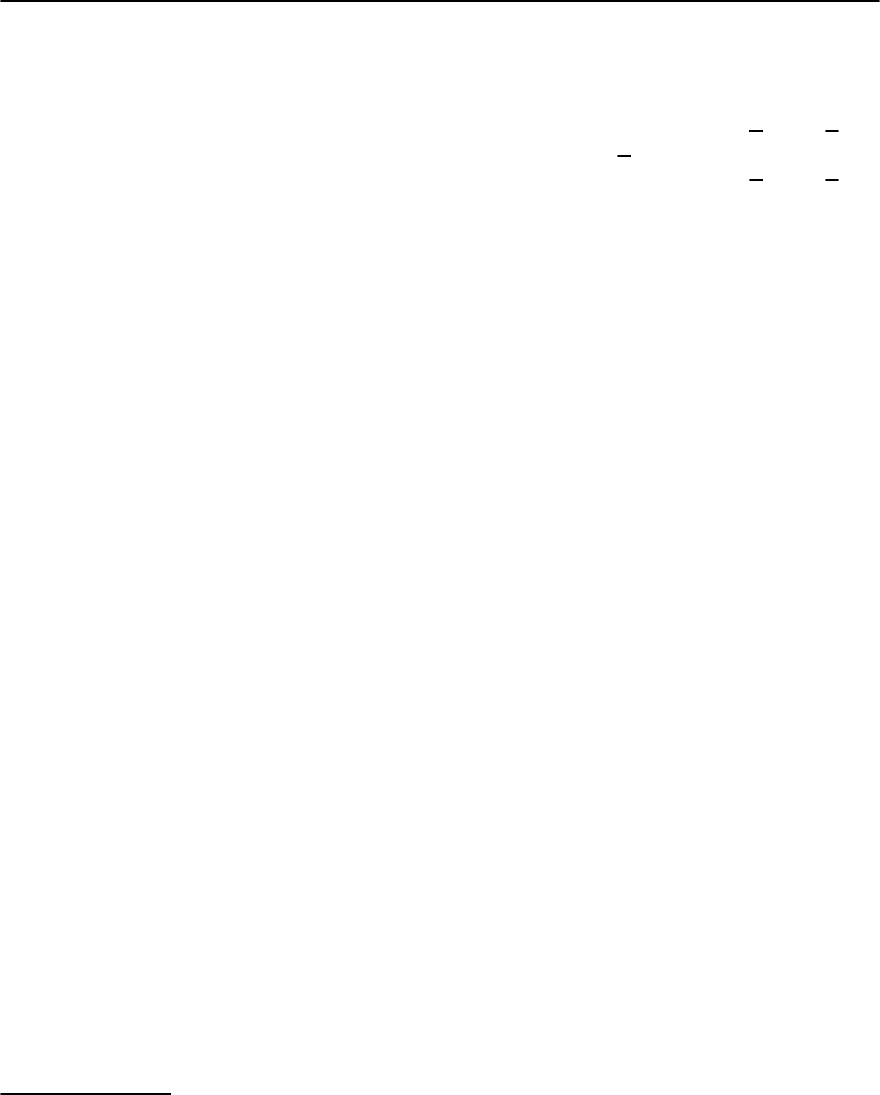
9 Principles of Josephson-Junction-Based Quantum Computation 339

of ﬂuctuating links N

/‹m

∼ 1.25×10

,whichis30

times greater than the channel density 4 ×10

/‹m

found in the above microwave resonance data. In ad-

dition, the density of frequency ﬂuctuators can also

be estimated from previous experiments.Various ex-

periments suggest there is approximately one reso-

nance per decade in frequency for junctions with an

area of 0.1 ‹m

[66,67]; this turns out to be twice

estimated for the microwave experiment described

above. Given they involved phenomena with char-

acteristic frequencies differing by orders of magni-

tude, the magnitude and density with frequency of

the microwave and 1/f noise measurements are in

rather good agreement; this strongly suggesting that

they arise from the same microscopic behavior in the

tunnel barriers. A compilation of 1/f noise data in-

dicates that junctions made from oxides of Al, Nb,

and Pb-In have similar magnitudes of 1/f noise [67].

Clearly alternatives to thermal or plasma oxidized

junctions should be investigated.

In conclusion,the spurious microwave resonances

in Josephson junction qubits significantly degrade

the amplitude of Rabi oscillations, and represent a

major challenge. These resonances can be under-

stood as arising from two-level ﬂuctuating links

within the tunnel barrier, which couple to the qubits

states through the critical current. Clearly, better

qubits will require better junctions.

9.3.4 Charge Qubits

We now discuss single qubit operations involving

charge qubits. As noted earlier all such operations

can be carried out using the gate voltage alone, and

we treat this approach first.

Operations Using the Gate Voltage Only

The Hamiltonian describing charge qubits was dis-

cussed in Sect. 9.2.4 [see Eq. (9.17)]. We start by as-

suming the qubit is in an“idle state”in which the gate

voltage V

is set at a value sufficiently far to the left

of the degeneracy point such that the eigenstates |0

and |1, Eq. (2.18), are close to the pure |↑ and |↓

states, Eq. (9.18), respectively. Switching the system

suddenly to the degeneracy point for a time t and

backproducesarotationinspinspace,

1−bit

(

)

=exp







⎛

⎜

⎝

cos

i sin

cos

⎞

⎟

⎠

(9.64)

where the angle ˛ = E

t. One can then produce a

superposition state with any chosen weights simply

by choosing the proper time interval t [62].On the

other hand when the system is biased slightly to one

side or the other, this produces a small shift in en-

ergies E

and E

with the result that these two states

precess at slightly different rates which, acting for a

time t, results in a rotation by an angle ˇ about the

x-axis; i.e., we can mimic a field B

.Henceacombi-

nation of the two parameters, V

and t, effectively

give control of B

and B

It turns out that unitary rotations by B

and B

are sufficient to perform all manipulations of a sin-

gle qubit. Implementing a sequence of no more than

three such elementary rotations one achieves any

unitary transformation of a qubit’s state.

The for-

mer example, with control of B

only, yields an ap-

proximate spin ﬂip for the situation in which the idle

point is far from degeneracy and E

 E

.Butaspin

ﬂip in the logical basis can also be performed exactly.

One switches from the idle point (corresponding to

Q = ...,−2, 0, 2,...,see Fig. 9.6) to the point where

the effective magnetic field is orthogonal to the idle

one (i.e., Q = ...,−1, 1,...),  = 

idle

+ /2. This

changes the Hamiltonian from

H =−E

(



idle

)

ˆ

H =−E

(



idle

+ /2

)

ˆ

/2. This is achieved by

increasing N

by E

/(4E

sin 2

idle

). When 

idle

 1

as above,the operating point lies near the degeneracy

point,  = /2.

Another way of manipulating the qubit is to use

resonant pulses, i.e., r.f. pulses with frequency close

to the qubit level spacing. We do not describe this

technique here as it is well known from NMR meth-

ods.

Up to this point we have been concerned with the

time evolution during elementary rotations involv-

This is the analogue of rigid body rotations where three successive rotations parameterized by the three Euler angles,

but involving only two axes, allow an arbitrary orientation of the body.

340 S.E. Shafranjuk and J.B. Ketterson

ing a single qubit. In practice, however, the quantum

state must be controlled for some time, for instance,

while other qubits are manipulated.Even when in an

idle state, = 

idle

,the energies of the two eigenstates

differ and hence their phases evolve relative to each

other, which leads to coherent oscillations, typical of

a quantum system in a superposition of eigenstates.

One must therefore keep track of this time depen-

dence with high precision, starting from the time t

when the manipulations are begun. In principle the

independent phase factors can be removed from the

eigenstates if all the calculations are performed in

the interaction representation, with the zero-order

Hamiltonian being the one at the idle point. How-

ever, one must then incorporate an additional time

dependence in the Hamiltonian during operations,

which is introduced by the transformation to the in-

teraction representation.

Thechoiceofthequbitlogicalbasisisbynomeans

unique. As follows from the preceding discussion,

one can perform x and z rotations in the charge ba-

sis, |↑ and |↓, which allows any unitary operation.

On the other hand, since one can perform any uni-

tary transformation, other logical basis can be used

as well. The Hamiltonian at the idle point is diago-

nal in the eigenbasis Eq. (9.23a,b) while the control-

lable part of the Hamiltonian, the charging energy,

favors the charge basis, Eq. (9.18). The preparation

procedure (thermal relaxation at the idle point) is

more easily described in the eigenbasis, while cou-

pling to the meter is diagonal in the charge basis. So

the choice of the logical states remains a matter of

convention.

Operations Combining SQUID Flux and Gate Voltage

The above discussion has shown that logic opera-

tions with a charge qubit can be performed using

the gate voltage alone. However it is clearly better

to have a second parameter available. The Josephson

coupling energy is such a parameter since it can be

tuned using the hybrid design; here two junctions

in a loop configuration replace the single Joseph-

son junction [61] as shown earlier schematically in

Fig. 9.12, and experimental realized with the de-

vices shown in Figs. 9.13 and 9.14. This so called “dc

SQUID”canbebiasedbyanexternalﬂux¥

,which

is coupled into the system through an inductive loop.

If the self-inductance of the SQUID loop is low, the

potential energy term in the Hamiltonian takes the

form [see Eq. (9.14)]

U =2E

cos





cos ' , (9.65)

where '

= ¥

/¥

and ¥

= hc /2e denotes the ﬂux

quantum. Here we assume that the two junctions are

identical with the same E

. The effective junction

capacitance is the sum of individual capacitances of

two junctions; in symmetric cases C

=2C

When the parameters are chosen such that only

two charge states play a role, one again arrives at

the Hamiltonian (9.14) but where now the effective

Josephson coupling,

= E

(¥

)=2E

cos '

, (9.66)

is tunable.Varying the external ﬂux ¥

by amounts of

order ¥

changes the coupling between 2E

and zero.

The SQUID-controlled qubitis thus described by the

ideal single-bit Hamiltonian, with the field compo-

nents B

(t)=ıE

(t)] and B

(t)=E

[¥

(t)]

controlled independently by the gate vol tage and the

ﬂux. If we fix conditions such that V

= V

deg

and

= ¥

/2, the Hamiltonian is zero, H

=0,andthe

state does not evolve in time. Hence there is no need

to control the total time t

from the beginning of the

manipulations. If we change the voltage or the cur-

rent, the modified Hamiltonian generates rotations

around the z or x axis respectively, which generate

the elementary one-bit operations. Typical time in-

tervals for single-qubit logic gates are determined

by the corresponding energy scales, which are of or-

der /E

, /ıE

for x and z rotations, respectively.

If only one of the fields, B

(t)orB

(t), is applied,

the time integrals of their envelopes determine the

result of the operation; these envelopes can then be

chosen to optimize the speed and simplicity of the

manipulations. The introduction of the SQUID not

only permits simpler and more accurate single-bit

manipulations, but also allows control of the two-bit

couplings.

Thetimeevolutionofthehybridqubitiscon-

trolled by i) applying microwave pulses (t)with

9 Principles of Josephson-Junction-Based Quantum Computation 341

Fig. 9.26. Relaxation time at the degeneracy point

frequency  = 

to the gate,and ii) by applying bias-

current pulses with a small amplitude (compared to

the critical current).Resonant modulation of the gate

voltage induces Rabi precession (see Sect. 9.3.1) be-

tween the two-qubit states; the bias-current can be

used to shift the qubit transition frequency. Starting

from |0, any superposition |¦  = a |0+ b |1can be

prepared. The relaxation following a  pulse for the

device shown in Fig. 9.14 is shown in Fig. 9.26.

For readout,one may implement a strategy similar

to the Stern and Gerlach experiment: theinformation

about the quantum state is transferred onto another

variable, the phase difference ' (' and '

are the

phase across the large junction and across the series

combination of the two junctions in the loop corre-

spondingly, see Fig. 9.14) and the two states are dis-

criminated via the supercurrent ﬂowing in the loop.

For this purpose,a trapezoidal readout N

pulse I

(t)

with a peak value slightly below the critical current,

= E

/

, is applied to the circuit. When start-

ing from

=0('

is the phase difference across

the large junction as shown in Fig. 9.14) the phases

' and '

grow during the current pulse, and con-

sequently a state-dependent supercurrent develops

in the loop. This current adds to the bias-current

in the large junction, and by precisely adjusting the

amplitude and duration of the I

(t)pulse,thelarge

junction switches during the pulse to a finite volt-

age state with a large probability p

for state |1 and

with a small probability p

for state |0. The effi-

ciency of this projective measurement is expected to

exceed = p

− p

for optimum readout conditions.

The readout part of the circuit has been tested [75]

by measuring the switching probability p as a func-

tion of the pulse height I

for a current pulse du-

ration of 

= 100 ns, at thermal equilibrium. The

discrimination efficiency was then estimated using

the calculated difference |0and |1 states. The value

obtained,  =0.6, was lower than the expected one,

possibly due to noise coming from the large band-

width current-biasing line.

Hybrid Qubit Manipulations

The switching of the large junction to the voltage

state was detected by measuring the voltage across it

with an amplifier at room temperature. By repeating

the experiment (∼ 10

times), the switching proba-

bility can be measured, which gives the weights of

the two states.One performs spectroscopic measure-

ments by applying a weak continuous microwave ra-

diation to the gate, which is suppressed just prior

to the readout current pulse. The variations of the

switching probability with the microwave frequency

display a resonance; Figure 9.27 shows the center fre-

quency as a function of the control parameters. Fig-

ure 9.28 shows the measured transition frequency

(symbols) as a function of reduced gate charge N

for a reduced ﬂux ' = 0 (right panel) and as a func-

tion of ' at N

=1/2 (left panel), at 15 mK. The

342 S.E. Shafranjuk and J.B. Ketterson

Fig. 9.27. Calculated transition frequency 

a function of the control parameters n

and

' = ı/2pi

Fig. 9.28. Measured center transition frequency (symbols)

as a function of reduced gate charge n

for reduced ﬂux

' =0(right panel)andasafunctionof' at n

=1/2(left

panel),at 15 mK. Spectroscopy is performed by measuring

the switching probability p (10

events) when a continu-

ous microwave radiation of variable frequency is applied

to the gate before readout. The continuous line shows best

fits used to determine circuit parameters. Inset:narrowest

lineshape, obtained at the saddle point (Lorentzian fit with

aFWHMof0.8MHz)

experimental measurement results of the narrowest

lineshape, obtained at the saddle point, are shown in

Fig. 9.29 along with a Lorentzian fit.

The linewidth in vicinity of the optimal point is

presented in Fig. 9.30. The optimal working point,

the linewidth was found to be minimal with a 0.8

MHz FWHM,corresponding to a Q of 2 ×10

.These

spectroscopic data allow one to determine the rele-

vant circuit parameters.

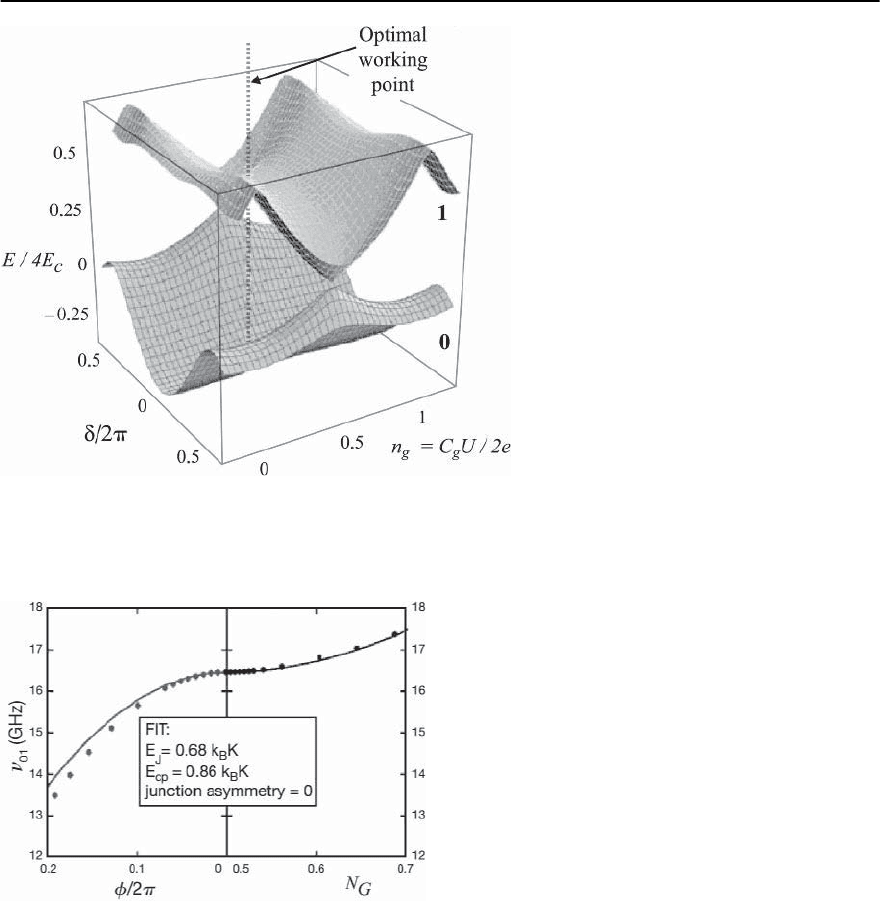
Preparation of a Coherent Superposition

Close to the optimal point, controlled rotations of

the spin can be performed using large amplitude

microwave pulses at the transition frequency. The

switching probabilityof a sinusoidal pulse as a func-

tion of pulse duration is shown in Fig. 9.31, and is

in agreement with the expected behavior for Rabi

oscillations (see Sect. 9.3.1). The linear dependence

of the Rabi frequency on the microwave amplitude

was used to calibrate the rotation angle.Note that the

amplitude of the Rabi oscillations is smaller than the

estimated efficiency. This may arise from relaxation

of the level population during the measurement it-

9 Principles of Josephson-Junction-Based Quantum Computation 343

Fig. 9.29. Narrowest lineshape, obtained at the

saddle point (Lorentzian fit with a FWHM of

0.8 MHz)

Fig. 9.30. Linewidth close to the optimal point

self. Better control is needed for achieving a perfect

“single-shot” readout.

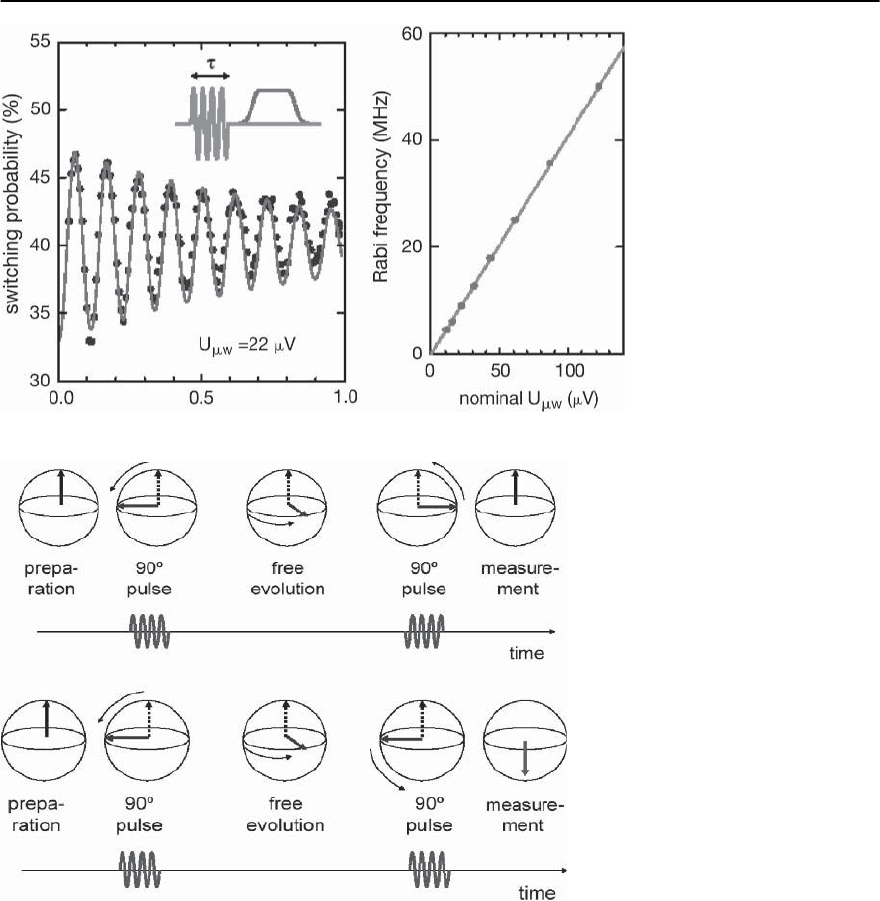
Measurement of the Coherence Time

The coherence time during free evolution can be ob-

tained using a two-pulse sequence with a delay dur-

ing which the qubit evolves freely; the sequence is

shown in Fig. 9.32. After the first pulse, the spin di-

rection rotates to a new position, which corresponds

to a mixed state.The final state depends on the phase

of the second pulse. If the pulse is inverted (shifted

by  as shown in the upper panel), the spin returns

to the initial position. However if the pulse is the

same, the spin ﬂips. Figure 9.33 shows the switching

probability for a given detuning of the microwave

frequency  after a two-pulse sequence as a func-

tion of the pulse delay t,at15mK.Noteitdisplays

decaying oscillations of frequency  , which corre-

spond to “beating” between the spin precession and

the external microwave field; this is equivalent to the

Ramsey fringe experiment.The envelope of the oscil-

lations yields the coherence time, which for the case

shown corresponds to 8000 free precession cycles.

344 S.E. Shafranjuk and J.B. Ketterson

Fig. 9.31. Left: Rabi oscillations

of the switching probability p

measured just after a resonant

microwave pulse of duration t.

Data taken at 15 mK for nomi-

nal amplitudes (dots,fromtop

to bottom). Solid lines are si-

nusoidal fits used to determine

the Rabi frequency. Right:test

of the linear dependence of the

Rabi frequency with the mi-

crowave amplitude

Fig. 9.32. Measuring the coherence life-

time

The measured coherence time is shorter than the

relaxation time T

=1.8 ‹s deduced from the expo-

nential decay of the switching probability when the

readout is delayed after a single pulse. Decoherence

of the quantum state is thus dominated by dephasing

and not by relaxation from the excited state to the

ground state.

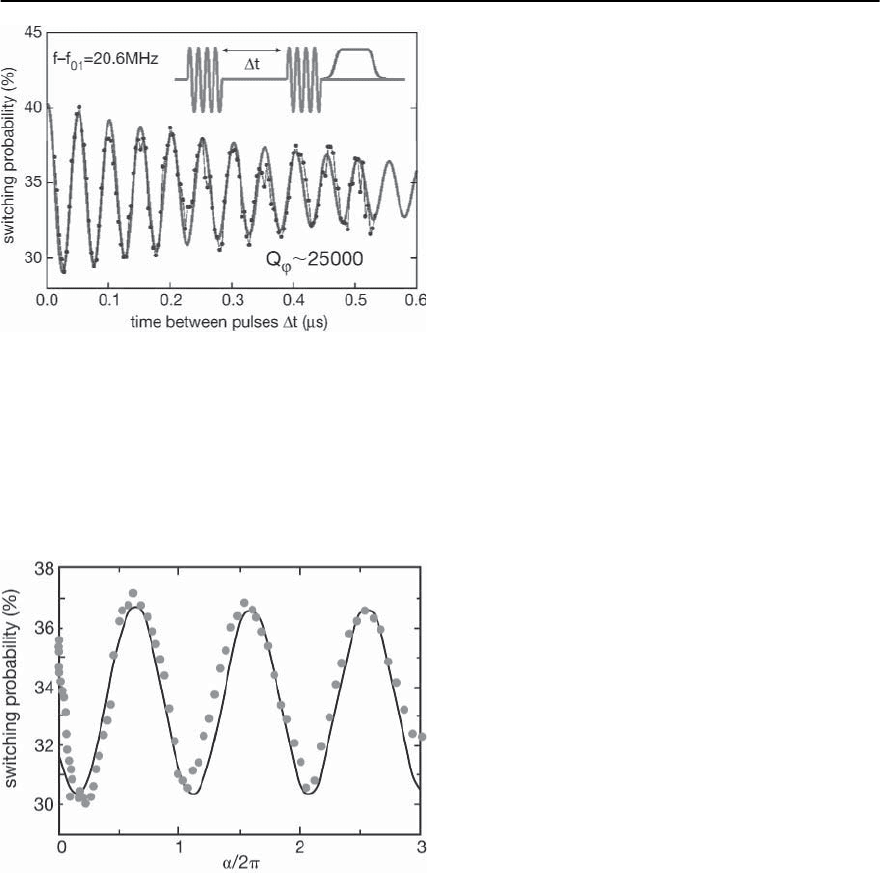
Full Qubit State Manipulation

When working at the optimal point, the two-pulse

sequence can be used to probe the phase shift that

is induced between both qubit states by a small adi-

abatic change of the bias current applied during a

pulse. The switching probability vs rotation angle ˛

induced by a 100 ns ramped bias supercurrent pulse

9 Principles of Josephson-Junction-Based Quantum Computation 345

Fig. 9.33. Do ts: switching probability after a two-pulse se-

quence as a function of the pulse delay t,at15mK.The

total acquisition time was 5 s. Continuous line: fit by an

exponentially damped sinusoid with frequency 20.6 MHz,

equal to the detuning frequency  ,anddecaytimecon-

stant T

=0.5 ‹s

Fig. 9.34. Switching probability following a two-pulse se-

quence as a function of the rotation angle ˛ induced by a

bias-current pulse with variable amplitude.The 100 ns bias

current pulse is applied between the two microwave pulses

applied between the two microwave pulses is shown

in Fig. 9.34. Combining bias-current pulses and mi-

crowave pulses, which correspond to two indepen-

dent rotation angles, one can produce any unitary

evolution of the qubit.

Adding and Removing Decoherence

When departing from the optimal point, the coher-

ence time T

decreases rapidly. By inserting a 

pulse between the two /2 pulses, NMR-like echo

experiments can be performed to probe the spec-

tral density of the noise sources responsible for de-

phasing (so-called homogeneous line broadening).

In this sequence, the random phases accumulated

during the two free evolution periods (i.e., between

the  pulses), with durations t

and t

,willcompen-

sate when t

= t

; provided the transition frequency

does not change on this time-scale. Echoes can be

observed at times for which Ramsey fringes (free in-

duction decay) are completely washed out.This indi-

cates that in this situation decoherence is essentially

due to charge ﬂuctuations at frequencies lower than

1 MHz. In the opposite limit, no echo was seen in ex-

periments attempting to probe the phase noise, sug-

gesting the phase noise extends over a wide range of

frequencies.

Controlling the quantum evolution of an individ-

ual qubit is a necessary first step towards functional

quantum circuits. It is however still necessary to im-

prove the coherence time by a factor ≈ 100,to achieve

high fidelity readout, and to implement controlled

qubit interactions. Coupling multiple quantronium

circuits can in principle be achieved using on-chip

capacitors and/or ultra small junctions. Coupling

schemes have been proposed for other Josephson

qubits as well [56, 57,76]. Thus in principle, quan-

tumgatescouldbeimplementedandprobedbymea-

suring quantum correlations induced in multi-qubit

entangled states.It seems that no fundamental obsta-

cle blocks the realization of an elementary quantum

processor based on Josephson junctions. Some ex-

periments on a two-qubitgate will be discussed next

in Sect. 9.4.

9.4 Quantum Oscillations in Two Coupled

Charge Qubits

9.4.1 The circuit

In this section we discuss experiments in which a

coherent coupling between two different qubits has

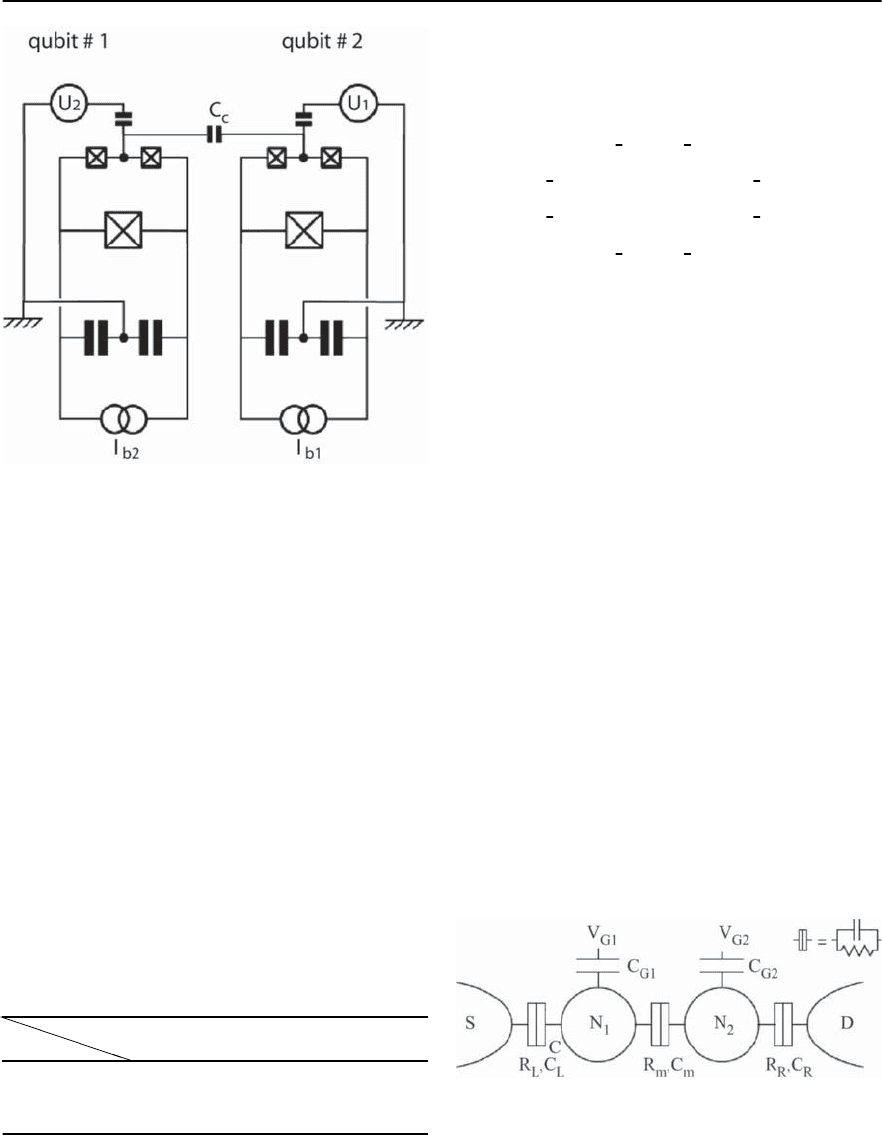
346 S.E. Shafranjuk and J.B. Ketterson

Fig. 9.35. Two-qubit gate with capacitive coupling

been observed [77]. A Cooper-pair box implemen-

tation was used for the individual qubits in which

two charge states, say |0 and |1, differing by one

Cooper pair are coherently mixed by Josephson cou-

pling [78–80]. As discussed in Sect. 9.3.4, quantum

state manipulation in such a system can be done us-

ing a non-adiabatic pulse technique and read-out can

be performed by a properly biased probe electrode.

However the experiments have been carried one step

further toward implementing quantum logic gates

by integrating two charge qubits which are coupled

electrostatically by an on-chip capacitor,C

,asshown

schematically in Fig. 9.35. The qubits have a SQUID

geometry to allow control of the Josephson coupling

to their reservoir. Both qubits have a common pulsed

gate (not shown in the figure) but separate dc gates,

probes and reservoirs.The pulsed gate has nominally

equal coupling to each box (see also Table 9.2).

Table 9.2. Quantum versus classical spin–spin correlations

for two qubits

Qubit 2

Qubit 1

xyz

x−10.5(< 0.33) 0.5 (< 0.33)

y0.5(< 0.33) −1 0.5 (< 0.33)

z0.5(< 0.33) 0.5 (< 0.33) −1

9.4.2 The Two-Qubit Hamiltonian

The Hamiltonian of the system in the two-qubit

charge basis |00, |10, |01 and |11 is given by:

H =

⎛

⎜

⎝

−

0−

−

0 E

−

0−

−

⎞

⎟

⎠

; (9.67)

here the total electrostatic energy of the system is

given by

− n2=E

− N

)

+ E

− N

)

+ E

− N

)(N

− N

) ,

(9.68)

, N

)=0, 1 is the number of excess Cooper

pairs in the first and the second box, E

J1,2

are the

Josephson coupling energies of the two boxes and

the reservoir, E

c1,2

=4e

2,1

/2(C

− C

)arethe

effective Cooper-pair charging energies, C

1,2

are the

sum of all capacitances connected to the correspond-

ing island 1(2) (including the mutual coupling ca-

pacitance C

, i.e., C

1,2

= C

L,R

+ C

G1,2

+ C

), and

G1,2

=(C

G1,2

+ C

)/2e are the normalized

charges induced on the corresponding qubit by the

d.c. and pulse gate electrodes. The detailed deriva-

tion of the Coulomb part of the Hamiltonian (9.67)

is given in [79]. The coupling energy E

depends not

only on C

, but also on the total capacitance of the

boxes: E

=4e

/(C

− C

); for spin effects see

Table 9.2.

A schematic of the classical electrostatic compo-

nents is shown in Fig.9.36.Applyingthe gate voltages

andV

controls diagonal elementsof the Hamil-

tonian given in Eq.(9.70).The circuit was designed to

Fig. 9.36. The electric circuit of the classic double-dot

system

9 Principles of Josephson-Junction-Based Quantum Computation 347

have E

J1,2

, E

< E

c1,2

; this ensures a coherent super-

position of the four charge states, |00, |10, |01,and

|11 in the vicinity of N

= N

=0.5(seealsoTa-

ble 9.2), while keeping other charge states separated

by large energy gaps, thereby justifying a four-level

description of the system. In the absence of Joseph-

son coupling,the ground-statecharging diagram(N

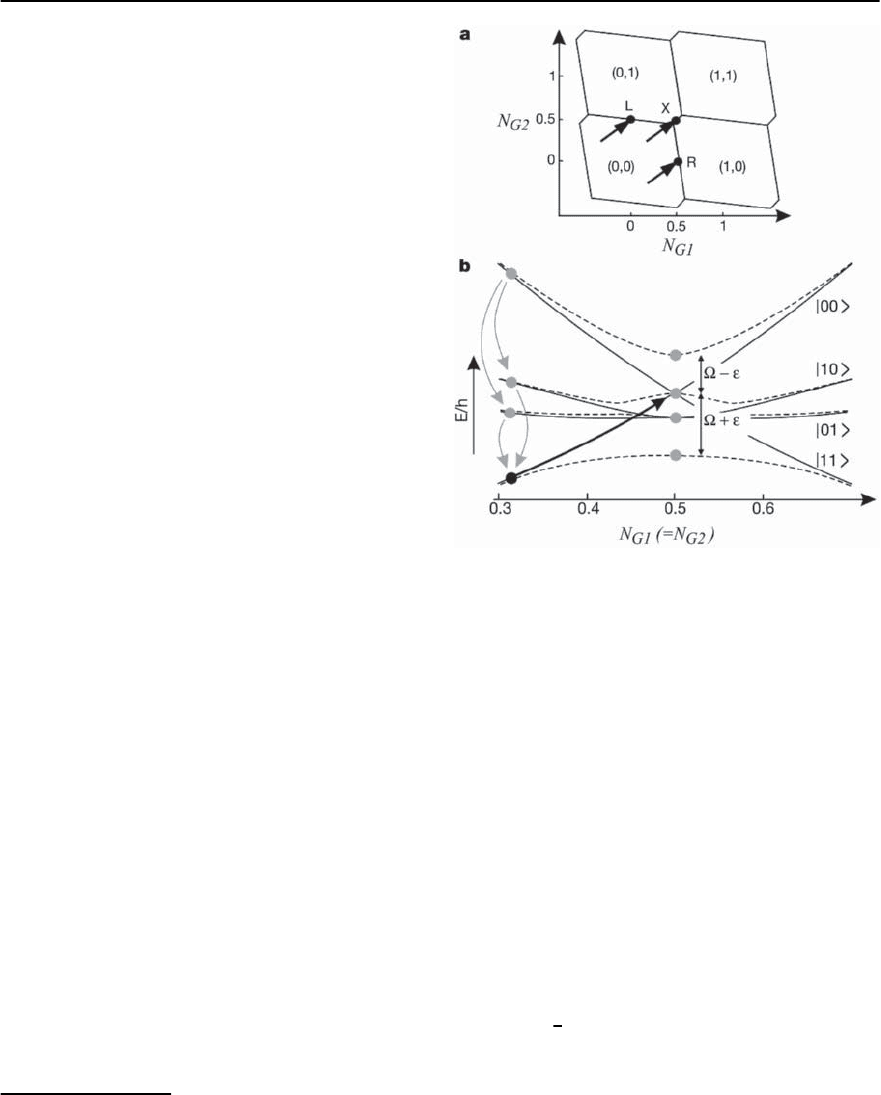
) shown in Fig. 9.37a consists of hexagonal cells

whose boundaries separate two neighboring charge

states with degenerate electrostatic energies.Accord-

ing to [81] the precise shape of the cells depends on

ratios of the inter-dotcapacitances.The points R and

L in Fig. 9.37a correspond to a degeneracy between

the states |00, |10 and the states |00, |01 differ-

ing by one Cooper pair in the first and the second

Cooper-pair box, respectively. If we choose the dc

gate charges n

and n

far from the boundaries

but within the (0,0) cell, then, because of the large

electrostatic energies, we can assume that the sys-

tem remains in the state |00. Since a pulse applied

to the gate couples equally to both qubits, the state

of the system moves along a line tilted by 45

◦

,as

indicated by arrows in Fig. 9.37a. The charging en-

ergy dominates except for the small Josephson cou-

pling which manifests itself on the boundaries where

charge states become superposed. If the system is

driven non-adiabatically to the points R or L, it be-

haves like a single qubit and oscillates between the

degenerate states with a frequency !

= E

J12

/.By

applyingvariouspulsesandmeasuringtheoscilla-

tions of the probe currents I

and I

, the Josephson

energies of each qubit can be determined. The ac-

curacy of the measured E

J1,2

is very high, since the

electrostatic coupling through C

has a minimal ef-

fect on !

1,2

near the points R and L.

At the ‘co-resonance’ point X (corresponding to

= N

=0.5), the system is doubly degener-

ate, i.e., E

= E

, E

= E

, and the dynamics of

the quantum evolution become more complex and

reﬂect the coupling between the qubits. The cross-

section of the energy bands through the point X is

showninFig.9.37b.Exactlyattheco-resonance,all

four-charge states are mixed and the state of the sys-

tem can be expressed in general as

Fig. 9.37. Pulse operation of quantum dot device: (a) tilting

of the two quantum dot states, (b) energy bands



(

)

= c

|00+ c

|10 + c

|01 + c

|11 , (9.69)

where |c

| (i =1, 2, 3, 4) are the time-dependent

probabilityamplitudes obeying anormalizationcon-

dition



i=1

= 1. Using the Hamiltonian (9.67)

and initial conditions, one can calculate the prob-

abilities |c

of each charge state. However, in the

read-out scheme, one measures a probe current I

proportional to the probability p

(1) of each qubit

having a Cooper pair on it, regardless of the state of

the other qubit; that is, I

∝ p

(1) ≡|c

+ |c

and

∝ p

(1) ≡|c

+ |c

. Assuming that the initial

state at t =0is|00, one obtains the time evolution

of these probabilities for an ideal rectangular pulse

shape of length t as

1,2

(

)



2−



1−

1,2



cos {

(

§ + "

)

t}

−



1+

1,2



cos {

(

§ − "

)

t}



(9.70)

In the spirit of our earlier analogy between the charging energy profiles and nearly free electron motion in one

dimension, for the coupled two qubit system the cell boundaries make up the two dimensional Brillouoin zone.

348 S.E. Shafranjuk and J.B. Ketterson

where 

1,2

=(E

J2,1

− E

J1,2

+ E

/4)/(4

), § =

((E

)

+(E

/2)

)

1/2

/2,and" =((E

−E

)

/2)

)

1/2

/2.Unlike the single qubit case,there are

two frequencies present, § + " and § − ",bothde-

pendent on E

, E

and E

.Onecanidentifythese

frequencies with the energy gaps in Fig. 9.37b.Note

that in theuncoupledsituation,whichcorrespondsto

= 0, each qubit oscillates with its own frequency

. However, the above consideration is valid only

in the ideal case when the pulse has zero rise/fall

time,andthetimeevolutionoccursexactlyatthe

co-resonance point.

9.4.3 Two Qubit Experiments

The idea of the experiment is shown schematically

in Fig. 9.37b. Startingfrom the |00state (shown as a

black dot), a gate pulse (represented by the solid ar-

row) brings the system to the co-resonance point. At

this point a microwave pulse is applied for a time t,

which produces a superposed state of theform (9.69).

as indicated by gray circles. After the pulse termi-

nates,the system evolvesin the superposed state until

it decays (indicated by the grey arrows) to the ground

state by emitting quasiparticles into the probe junc-

tions biased at V

b1,2

≈ 600 ‹eV. To accumulate a

signal, a series of 3 × 10

pulses was applied to the

Fig. 9.38. Quantum oscillations in two

coupled qubits. The upper two traces

depictsingle qubit like oscillations,cor-

responding to the points R and L in

Fig. 9.37a; the lower figures involve

states near theco-resonance pointX (in

the “corner”), where strong four-state

superpositions occur