Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

308 V. Chandrasekhar

=−

ET

cosh





⎡

⎣



(E, x)

⎤

⎦

−1

(8.239)

We then obtain from Eq. (8.193)

=−

DT



cosh

(E/2k

⎡

⎣



(E, x)

⎤

⎦

−1

. (8.240)

As with the electrical conductance, we can define a

thermal diffusion coefficient

(E, x)=DM

(E, x) , (8.241)

and a spectral thermal conductance

(E)=G

thN

⎡

⎣



(E, x)

⎤

⎦

−1

, (8.242)

where G

thN

is related to the normal state electrical

conductance by Eq. (8.17)

thN

= G



T . (8.243)

Finally, the thermal conductance itself is given by an

integral over energy



2(k



(E)

cosh

(E/2k

. (8.244)

Of course, as noted by Andreev [36], the thermal

conductance of a normal metal wire sandwiched be-

tween a normal-metal reservoir on one end and a

superconducting reservoir on the other end must

vanish, since the superconductor acts as a ther-

malinsulator,sothatnothermalcurrentcanﬂow

through the device as a whole.However,onemay con-

sider a normal-metal wire with the superconducting

reservoir connected off to one side, so that it does

not block the ﬂow of thermal current through the

proximity-coupled wire. One may then consider the

thermal conductance of the normal metal wire it-

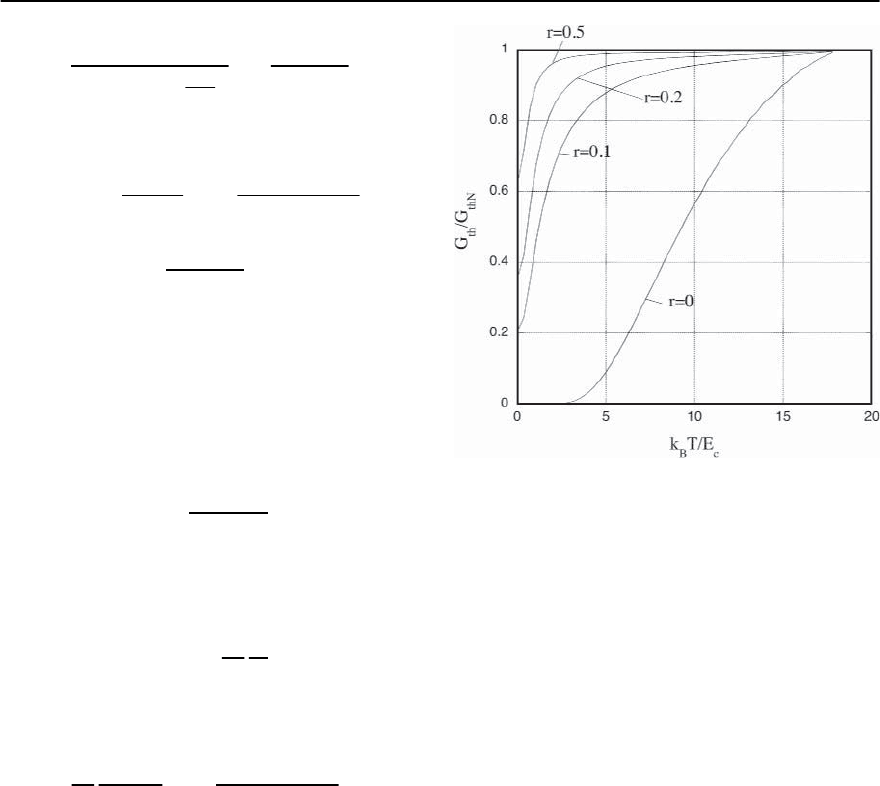
self. Figure 8.7 shows the thermal conductance of

Fig. 8.7. Thermal conductance G

of a normal wire con-

nected to a superconducting reservoir on one end, and a

normal metal reservoir on the other, as a function of the

normalized temperature T, for a number of different val-

ues of the interface barrier parameter r.Thegapissetto

be  =32E

, corresponding to a transition temperature of

T =18.14E

this geometry, as a function of temperature, for dif-

ferent transmissivities of the interface barrier. The

thermal conductance shows a monotonic decrease

as T is lowered below T

, although there are no dis-

tinct features at any particular temperature, unlike

for the electrical conductance. In a superconductor,

the exponential decrease in the thermal conductivity

is associated with the opening of the gap in the quasi-

particle density of states,since it is the quasiparticles

that carry the thermal current.Noting the decreasein

the density of states in the proximity-coupled normal

metal wire, shown in Fig. 8.6, it is not surprising that

this system will also show a decrease in the thermal

conductance. The thermal conductance of the wire

is strongly dependent on the transmission of the NS

interface, characterized by the parameter r,andap-

proaches the normal state thermal conductance as r

increases.

The thermal conductance of Andreev interferom-

eters has recently been measured [37], and calcula-

8 Quasiclassical Theory of Superconductivity 309

tions of the thermal conductance of this more com-

plicated geometry have also been performed [38].

We note here again that, in our current approxi-

mation, a small voltage drop across the S/n–wire/N

device will not result in a contribution to the thermal

current through the system, since any terms propor-

tional to voltage in the expansion of h

will cancel.

This is the converse of the case for the electrical cur-

rent, where a small temperature drop did not con-

tribute to the electrical current, emphasizing again

that the conventional quasiclassical approximation

cannot take into account thermoelectric effects.

8.9.2 Superconductor-Metal Bilayer

Instead of a normal reservoir on one side of the wire,

if we consider a wire of length L connected only

on one end to a superconducting reservoir (with

the other end open), then a true gap in the den-

sity of states opens up in the proximity-coupled nor-

mal metal. The magnitude of the gap is related to

; hence, one can consider the proximity-coupled

normal-metal in this case as a superconductor with

agapofE

If the superconductor is not a reservoir,but a thin

layer itself, then one will suppress superconductivity

in the superconducting layer due to the proximity of

the normal metal, an inverse proximity effect. The

suppression of superconductivity is expected to re-

duce the gap in the superconductor.It is an interest-

ing exercise to calculate the transition temperature

of the bilayer in the quasiclassical approximation.

We shall loosely follow here the treatment given by

Martinis et al. [39] and Gu´eron [40].

Let the thickness of the superconductor be t

,and

the thickness of the normal metal t

.Wetakethe

origin,x = 0, at the NS interface; the superconductor

extends from x =−t

to x =0,andthenormalmetal

from x =0tox = t

. Near the transition, the order

parameter in the superconductor is small, so we may

the small  limit of Eq. (8.215b). Since the phase is

not important in this problem, we take  =0.The

resulting equation is

 +2Ei −2i =0, (8.245)

wherewehaveassumedthatthegaugeischosenso

that  is real. Let us assume that  at x =0inthe

superconductor is 

, and that variations of  about

this mean value aresmall.Under these conditions,we

can also assume that the gap  in the superconductor

is uniform.We can then expand 

to second order

in x



= 

+ ax + bx

. (8.246)

Now, at x =−t

,(andalsoatx = t

), we have a vac-

uum interface, where @

 =0.Hencea =2bt

,and

from the differential equation (8.245) taken at x =0,

b =(i/D)( − E

), so that



= 

( − E

)(2t

x + x

) . (8.247)

Similarly



= 

E

(2t

x − x

) . (8.248)

From the boundary condition Eq. (8.222b), we have

the two equations

2irt

( − E

)=

− 

, (8.249a)

2irt

E

= 

− 

. (8.249b)

Solving this pair of equations for 

,wehave





+ t

)+4r

−2irDt

+ t

)

+4r

. (8.250)

Putting this into Eq. (8.229) for the gap, with T = T

and with the approximation that sinh()  ,we

obtain

1=N





tanh(E/2k

) (8.251)



1−

+ t

)

+ t

)

+(4r



The first term in the square brackets gives the bare

transition temperature T

of the superconducting

film, and the second term corresponds to the correc-

tions associatedwiththe inverse proximity effect.For

a perfect interface, with r = 0, the suppression of T

310 V. Chandrasekhar

is directly proportional to the normal fraction of the

bilayer,andT

→ 0ast

increases.For a highly resis-

tive barrier (r →∞), the second term in the square

brackets goes to zero, so that there is little effect of

the normal metal film on T

of the superconducting

film, as expected.

8.9.3 The SNS Junction and And reev Interferometers

As our final example of the application of the qua-

siclassical equations of superconductivity, we con-

sider the case of a dirty SNS junction. The model we

consider is a normal metal wire of length L sand-

wiched between two superconducting reservoirs. As

is well known, the application of a phase difference

between the two superconducting reservoirs will re-

sult in the ﬂow of a supercurrent through the nor-

mal wire. The phase difference can be applied, for

example, by connecting one of the superconducting

reservoirs to the other, thereby forming a loop with

two different arms, one superconducting and one

normal. This configuration is commonly called an

Andreev interferometer. The phase between the two

superconducting reservoirs can be varied by apply-

ing an Aharonov–Bohm type magnetic ﬂux through

the area of the loop; in this respect, we put together

all contributionsin the gauge-invariant phase .Due

to the single-valued nature of the wave functions, a

phase factorof 2¥/¥

is picked up in goingaround

the loop, where ¥ is the magnetic ﬂux threading the

Andreev interferometer, and ¥

= h/2e is the super-

conducting ﬂux quantum. In a superconductor, the

supercurrent I

that is generated is directly propor-

tional to the phase gradient; if I

is small compared

to the critical current I

, the phase dropped across

the superconductor will be small. Since I

of the su-

perconducting part of the Andreev interferometer is

so much greater than the critical current of the prox-

imity coupled normal-metal wire, most of the phase

change will occur across the length L of the normal

metal wire.

This fact allows us to map theAndreev interferom-

eter that is coupled with an Aharonov–Bohm ﬂux ¥

to a SNS system with a phase difference  =2¥/¥

across it. In terms of our model, we consider the su-

perconductors to be reservoirs; this means apply-

ing a boundary condition for the gauge-invariant

phase  at the superconducting reservoirs. For our

purposes, we apply this boundary condition anti-

symmetrically, with a phase 

=−¥/¥

at the

superconducting reservoir at x =0,and

= ¥/¥

at the superconducting reservoir at x = L.Wethen

must solve Eq. (8.215) in the normal-metal wire for

 and ,with = 0, subject to the boundary con-

dition for  noted above, and the boundary condi-

tion  = 

(where 

is given by Eq. (8.220)) at

both x =0andx = L. In general, both  and 

are complex functions of x and E, and the solution

of Eq. (8.215) must be done numerically. Following

Yip [41], we consider first the supercurrent Q,given

by Eq.(8.218).Some insight into the contributionsto

can be gained by looking again at the case of a bulk

superconductor. From Eq. (8.202), the major contri-

bution to j

comes from energies near the gap. For a

long proximity wire with E

< , however, the major

contribution comes from energies of order E

.Fig-

ure 8.8(a) shows a plot of Q as a function of energy

for various values of the phase difference  between

the two superconducting reservoirs, for the case of

a perfectly transparent interface, and  =32E

.Of

course, for zero phase difference, the supercurrent

vanishes. As  is increased from zero, there is a peak

in Q(E)atE  6E

. This peak moves down in en-

ergy as  increases. At larger values of E, Q becomes

negative. For shorter wires, this region of negative Q

is less prominent. The total supercurrent is given by

the second term in Eq. (8.192)

= eN



dEQ(E)h

(E) , (8.252)

and therefore depends also on the distribution of

quasiparticles. Any change in this distribution will

affect the supercurrent.For example,the distribution

can be changed by increasing the temperature, which

has the result of decreasing the supercurrent. As we

demonstratedinthe introduction,anon-equilibrium

quasiparticle distribution can also be generated by

injecting a normal current into the proximity wirein

the SNS geometry by attaching two additional leads

to the center of the normal wire, forming a normal

cross, with two of the wires attached to supercon-

ducting reservoirs, and the two other wires attached

8 Quasiclassical Theory of Superconductivity 311

Fig. 8.8. (a) Spectral supercurrent Q in a normal wire between two superconducting reservoirs, as a function of the nor-

malized energy E/E

, for different values of the phase difference  between the superconducting reservoirs. (b) Geometry

of an Andreev interferometer, essentially a cross with one arm connected to superconducting reservoirs, and the other

arm connected to normal reservoirs

to normal reservoirs, as shown in Fig. 8.8(b). The

current in the SNS junction is then a function of

the current injected between the normal reservoirs,

and the supercurrent can even change sign depend-

ing on the magnitude of the injected normal cur-

rent [41,42].This effect has been observed in recent

experiments [43].

Due to long-range phase coherence, the Green’s

function in the arms of the cross attached to the

normal reservoirs will also depend on the phase dif-

ference between the two superconducting reservoirs

in the structure shown in Fig. 8.8(b). Consequently,

the electrical and thermal conductance measured

between the two normal reservoirs will also be a

periodic function of the phase difference between

the two superconducting reservoirs. Experimentally,

both theelectrical conductance [44–46] and the ther-

mal conductance [37] of such Andreev interferome-

ters have been found to oscillate periodically with

an applied external ﬂux, with a fundamental period

of 

= h/2e. Periodic oscillations are also observed

in the thermopower of Andreev interferometers [47],

although these thermopower oscillations cannot be

described within the framework of the current qua-

siclassical theory.

8.10 Summary

The quasiclassical theory of superconductivity has

proved to be a powerful tool for the quantitative de-

scription of long-range phase coherent phenomena

in diffusive proximity coupled systems. As we have

shown,the linear electrical and thermal conductance

of complicateddevicesincorporating normaland su-

perconducting elements can be calculated in princi-

ple,although the solutionsfrequently involve numer-

ical techniques. Extension to the nonlinear regime,

with finite voltages across the normal reservoirs, is

also conceptually straightforward, although numer-

ically challenging.

Application of finitevoltages to the superconduct-

ing elements is trickier,as it involves time dependent

evolution of thephase,andis only beginning to be ex-

amined theoretically. Finally, the quasiclassical the-

ory for diffusive systems, in its present form, does

312 V. Chandrasekhar

not deal at all with thermoelectric phenomena. Ex-

tensions to incorporatethermoelectric effects in the

theoretical framework have been attempted [48], but

still require further work to be complete.

Acknowledgements

It is a pleasure to acknowledge illuminating dis-

cussions with Wolfgang Belzig, John Ketterson and

Zhigang Jiang. This work was supported by the US

National Science Foundation through grant number

DMR-0201530.

References

1. G. Eilenberger, Z. Phys 214,195 (1968)

2. A. Schmid and G. Sch¨on,J.Low.Temp.Phys.20, 207 (1972)

3. G.M. Eliashberg, Zh. Eksp. Teor. Fiz. 61, 1254 (1971), Sov. Phys. JETP 34, 668 (1972)

4. A.I. Larkin and Yu. N. Ovchinnikov, Zh. Eksp. Teor. Fiz. 68, 1915 (1976), Sov. Phys. JETP 41, 960 (1976)

5. A.I. Larkin and Yu. N. Ovchinnikov, Zh. Eksp. Teor. Fiz. 73, 299 (1977), Sov. Phys. JETP 46, 155 (1978)

6. C.-R.Hu,Phys.Rev.B21, 2775 (1980)

7. J.W. Serene and D. Rainer, Physics Reports 101, 221 (1983)

8. G. Sch¨on, In: Nonequilibrium Superconductivity, ed. by D.N. Langenberg and A.I. Larkin (Elsevier, 1986)

9. A.G. Aronov, Yu.M. Gal’perin,V.L. Gurevich and V.I. Kozub, Nonequilibrium properties of superconductors (transport

equation approach),In:Nonequilibrium Superconductivity, ed. by D.N. Langenberg and A.I. Larkin (Elsevier, 1986);

Adv. Phys. 30, 539 (1981)

10. J. Beyer, C.J. Pethick and J. Rammer, Pair breaking in nonequilibrium superconductors,In:Nonequilibrium Supercon-

ductivity, ed.by D.N. Langenberg and A.I. Larkin (Elsevier,Amsterdam, 1986)

11. J.Rammer and H. Smith, Rev. Mod. Phys.58, 323 (1986)

12. H. Smith and H.H. Jensen, Transport Phenomena (Clarendon, Oxford,1989)

13. A.F. Volkov,A.V. Zaitsev and T.M Klapwijk, Physica C 210, 21 (1993)

14. C.J.LambertandR.Raimondi,J.Phys.:Condens.Matter10, 901 (1998)

15. A.F.Volkov and V.V. Pavlovskii, In: Proceedings of the AIP Conference: Lectures on Superconductivity in Networks and

Mesoscopic Systems (New York,1998)

16. A.A. Golubov, F.K. Wilhelm,and A.D. Zaikin, Phys. Rev. B 55, 1123 (1997)

17. F.K. Wilhelm, A.D. Zaikin and G. Sch¨on,J.LowTemp.Phys.106, 305 (1997)

18. W.Belzig,F.K.Wilhelm,C.Bruder,G.Sch¨on and A.D. Zaikin, Superlattices and Microstructures 25, 1251 (1999)

19. Yu.V. Nazarov, Superlattices and Microstructures 25, 1221 (1999)

20. K.E. Nagaev, Phys. Lett. A 169, 103 (1992); Phys.Rev. B 52, 4740 (1995)

21. See, for example, F. Pierre, H. Pothier, D. Esteve, M.H. Devoret, A.B. Gougam, and N.O. Birge, In: Kondo Effect and

Dephasing in Low-Dimensional Metallic Systems, ed. by V. Chandrasekhar, C. Van Haesendonck and A. Zawadowski,

NATO Science Series, vol. II/50 (Kluwer, Dordrecht, 2001)

22. J.M. Ziman, Principles of the Theory of Solids, 2nd edn.(Cambridge University Press, Cambridge, 1972)

23. E.M. Lifshitz and L.P. Pitaevskii, Physical Kinetics, Vol. 10 of the Landau and Lifshitz Course of Theoretical Physics

(Pergamon, Oxford,1981)

24. L.P. Kadanoff and G. Baym, Quantum Statistical Mechanics (Addison-Wesley,Redwood City, 1962)

25. J.B. Ketterson and S.N. Song, Superconductivity (Cambridge University Press,Cambridge 1999)

26. A.A. Abrikosov, L.P. Gor’kov and I.E. Dzyaloshinski, M

ethods of Quantum Field Theory in Statistical Physics (Dover,

New York,1975)

27. M. Tinkham,Phys.Rev. B 6,1747 (1972)

28. A.L. Shelankov, J. Low Temp. Phys.60, 29 (1985)

29. K.D. Usadel, Phys.Rev. Lett.25, 507 (1970)

30. A.V.Zaitsev,Zh.Eksp.Teor.Fiz.86, 1742 (1984),Sov. Phys. JETP 59, 1015 (1985)

31. M.Yu.KuprianovandV.F.Lukichev,Zh.Eksp.Teor.Fiz.94, 139 (1988), Sov. Phys.JETP 67, 1163 (1988)

8 Quasiclassical Theory of Superconductivity 313

32. B.L.Altshuler,P.A. Lee and R.A.Webb, Mesoscopic Phenomena in Solids (North-Holland, Amsterdam, 1991)

33. See, for example, P. Charlat, H. Courtois, Ph. Gandit, D. Mailly, A.F. Volkov and B. Pannetier, Phys. Rev. Lett. 77, 4950

(1996)

34. P.G. de Gennes, Superconductivity of Metals and Alloys (Addison-Wesley, Redwood City, 1966)

35. S. Gu´eron,H.Pothier,N.O.Birge,D.Esteve,and M.H.Devoret,Phys.Rev.Lett.77, 3025 (1996)

36. A.F. Andreev, Zh. Eksp. Teor. Fiz. 46, 1823 (1964), Sov. Phys. JETP 19, 1228 (1964)

37. Z. Jiang and V. Chandrasekhar, Phys. Rev. B 72, 020502(R) (2005)

38. Z. Jiang and V. Chandrasekhar, Phys. Rev. Lett. 94, 147002 (2005)

39. J.M. Martinis, G.C. Hilton, K.D. Irwin and D.A. Wollman, Nucl. Instrum. Methods Phys. Res.A 444, 23 (2000)

40. S. Gu´eron, PhD thesis, Universit´e Paris 6 (1997)

41. S.-K.Yip, Phys. Rev. B 58,5803 (1998)

42. F.K.Wilhelm, G. Sch¨onandA.D.Zaikin,Phys.Rev.Lett.81, 1682 (1998)

43. J.J.A. Baselmans, A.F. Morpugo, B.J. van Wees and T.M Klapwijk, Nature 397, 43 (1999)

44. H. Pothier, S. Gu´eron, D. Esteve, and M.H. Devoret, Phys. Rev. Lett. 73, 2488 (1994)

45. V.T. Petrashov,V.N.Antonov, P.Delsing, andT. Claeson, Phys. Rev. Lett. 74, 5268 (1995)

46. S.G.denHartog,B.J.vanWees,T.M.Klapwijk,Yu.V.Nazarov andG.Borghs,Phys.Rev.B56, 13738 (1997)

47. J. Eom, C-J Chien and V. Chandrasekhar, Phys. Rev. Lett. 81, 437 (1998)

48. F.Wilhelm,PhD thesis, Universit¨at Karlsruhe (2000)

9 Principles of Josephson-Junction-Based Quantum Computation

S. E. Shafranjuk Department of Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA

J.B. Ketterson Department of Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA

9.1 Introduction ..............................................................................316

9.2 Josephson-Junction-Based Qubits ...........................................................319

9.2.1JunctionParametersandEnergetics.....................................................319

9.2.2TheBasicJosephsonQubitcategories....................................................320

9.2.3PhaseQubits..........................................................................320

9.2.4ChargeQubits........................................................................322

9.2.5FluxQubits...........................................................................327

9.3 Single Qubit Dynamics .....................................................................329

9.3.1TransitionsWithinTwo-LevelSystems;theRabiFrequency................................329

9.3.2Manipulation,ReadoutandDecoherence ................................................331

9.3.3PhaseQubits..........................................................................332

9.3.4ChargeQubits........................................................................339

9.4 Quantum Oscillations in Two Coupled Charge Qubits ..........................................345

9.4.1TheCircuit...........................................................................345

9.4.2TheTwo-QubitHamiltonian............................................................346

9.4.3TwoQubitExperiments................................................................348

9.5 SISIS Two-Qubit Gate with Intrinsic Coupling ................................................350

9.5.1ProximityCouplinginaMultilayeredJunction...........................................351

9.5.2Inter-QubitCouplingEnergy ...........................................................353

9.5.3ControloftheInter-qubitCoupling.....................................................354

9.5.4AdditionalControlUsingTangentialSupercurrents.......................................355

9.5.5LeakageandFidelityoftheTwo-QubitGate..............................................357

9.6 Conclusions ...............................................................................361

Appendix. Elementary Quantum Logic Operations ...............................................362

A.1BooleanLogic..........................................................................362

A.2RequiredProperties ....................................................................363

A.3UniversalQuantumGates ...............................................................363

A.4QuantumSumandCarry................................................................364

A.5Shor’sAlgorithm.......................................................................364

A.6Conclusions............................................................................365

References................................................................................365

316 S.E. Shafranjuk and J.B. Ketterson

9.1 Introduction

One of several approaches that have been proposed

for implementing quantum information process-

ing is to utilize mesoscopic, artificially fabricated,

solid-state structures which,based on the underlying

physics, can be designed to behave as single “quan-

tum particles.” The primary reason for a solid state

approach is that it offers the likelihood of scalabil-

ity by exploitingfabricationstrategies made possible

by the semiconductor industry; scalability is essen-

tial if quantum information processing is to become

a practical reality. Aside from practical applications,

the study of such mesoscopic structures is of interest

in its own right.

Quantum information processing is typically

based on an assembly of quantum bit devices, so-

called qubits [1], a term the community has adopted.

Such devices involve externally controlled transi-

tions between two quantum states, |0and |1,corre-

sponding to two different eigenenergies, E

and E

There are now many proposals for qubits involving

various two-level systems. However such elementary

quantum logic devices must satisfy strict require-

ments if they are to be used as quantum logic el-

ements in realistic information processing circuits.

A practical circuit utilizing qubits must permit: (i)

controlled manipulations of the quantum state of

each qubit without disturbing adjacent elements and

(ii) controlled inter-qubitcoupling;also required are

(iii) a limited inﬂuence of the external environment

and (iv) sufficientlylong dephasing and decoherence

times [2,3]. If these requirements cannot be fulfilled,

reliable qubit circuits cannot be realized, which cur-

rently eliminates many qubit proposals.

Quantum computation (QC) employs and re-

quires a programmable unitaryevolutionof the indi-

vidual qubits [4]. Because the proposed systems ex-

ploit quantum parallelism and quantum algorithms,

they are capable of efficiently solving certain classes

of problems, which are intractable on classical com-

puters. A striking example is the factorizing of large

numbers [5], which is far more efficient on a quan-

tum computer than on a conventional one.

Along with the developmentof the theory of quan-

tum information,there has been a parallel interest in

finding physical systems where quantum computa-

tioncanbeimplemented.Towardthisend,onemust

first identify a suitable two-level system, which is

sufficiently decoupled from any source of decoher-

ence [6], and for which the coupling among like el-

ements can be controlled, thereby allowing the real-

ization of single- and two-qubit operations. In prin-

ciple one can then carry out any computational task

if requirements (i)–(iv) are fulfilled [2,3,7]

For the implementation of quantum algorithms

various physical systems have been suggested. Some

of these proposals involve: ions in traps, [8] QED

cavities, [9] and NMR-based approaches [10]. To

achieve large-scale integrability and ﬂexibilityin the

design, approaches involving micro- or even nano-

technology are being examined including: small-

capacitance Josephson junctions [11–15], coupled

quantum dots [16, 17], neutral atoms in optical

lattices [18], and phosphorus dopants in silicon

crystals1 [19]. Most of the solid-state based ef-

forts concentrate on superconducting qubits,specif-

ically Josephson junction based qubits [3], and we

will review recent junction-based experiments and

their theoretical interpretation. The experimental

evidence for the superposition of charge states in

Josephsonjunctions[20,21]andrecentachievements

in controlling the coherent evolution of quantum

states in a “Cooper pair box” [22] make supercon-

ducting circuits very promising candidates to imple-

ment solid state quantum computing.

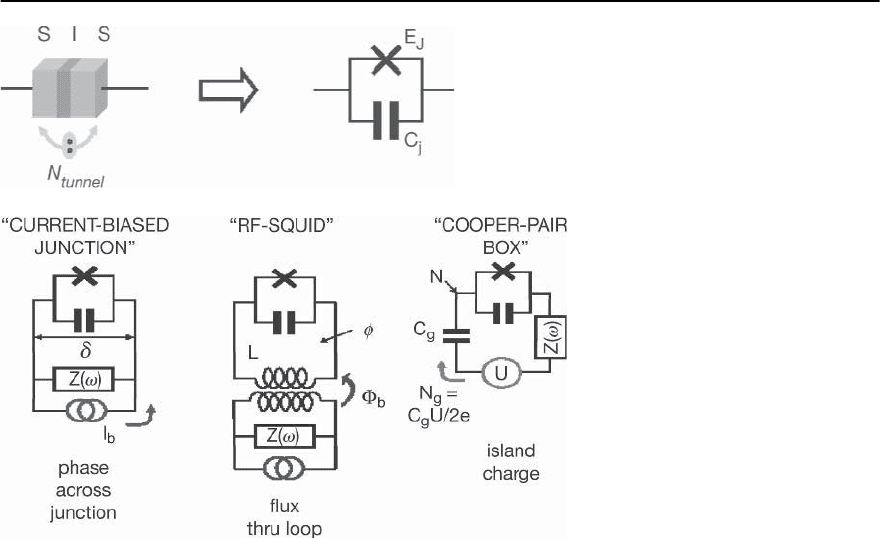
Figure 9.1 shows a schematic representation of

a Josephson junction. Superconducting qubits ex-

ploit Cooper pair tunneling between the superﬂuid

condensates in adjacent superconducting electrodes.

The Josephson interaction across a dielectric bar-

rier has an intrinsic non-linear origin, which plays

an important role in the design of the qubit devices.

Josephson junction based qubits, depending on the

external configuration, exploit the order-parameter

phase, magnetic ﬂux, or electric charge, as shown

schematically in Fig. 9.2. Combinationsof these con-

figurations are also exploited.

This chapter is organized as follows.In Sect.9.2 we

brieﬂy describe the three Josephson junction based

qubit devices, the phase qubit, the charge qubit, and

the ﬂux qubit,along with experiments on some spe-

9 Principles of Josephson-Junction-Based Quantum Computation 317

Fig. 9.1. A schematic representation of a Josephson

junction and the equivalent circuit

Fig. 9.2. The three major Josephson-

junction-based qubit implementations

cific implementations. We also discuss so-called hy-

brid qubits that combine aspects of both charge and

ﬂux qubits.

Section 9.3 starts with a review of the quantum

mechanics of two-level systems, which underlies all

qubit operations. This is followed by a discussion of

the effects of decoherence arising from coupling to

external degrees of freedom. It is crucial to maintain

the coherence of the two basic qubit states during

a quantum computation [2]. The decoherence time,



dec

, of the individual qubits should be larger, by a

factor of order 10

,thanatimet

, required to carry

out a single operation; one can then carry our ar-

bitrarily long quantum computations by exploiting

various error-correction techniques. In solid state

implementations, due to the complexity of the en-

vironment, there are many degrees of freedom that

can couple to the qubit states and cause decoherence.

Compared with the photonic andatomic qubit strate-

gies, the superconducting persistent current qubit

is subject to more severe decoherence. Dominant

sources of decoherence include both “internal” ef-

fects, such as dissipation, e.g., from quasiparticle re-

sistance, and dephasing from qubitinteractions with

the external environment. These mechanisms de-

pend strongly on the geometry, and on ﬂuctuations

of the environment (e.g., nuclear spin ﬂuctuations

in aluminum), on background charge noise, and on

noise in the control currents. It is also possible to

couple to an environmental degree of freedom,with-

out a dissipative mechanism, that will still lead to

decoherence. We will outline the general formalism

that can be used to deal with the dephasing caused

by thermal ﬂuctuations, including quasiparticle dis-

sipation, charge oscillations, nuclear spin relaxation,

etc. However we will not, for the most part, try to

analyze such mechanisms in detail.

Section 9.3 then goes on to discuss some experi-

ments on single qubit operations that have been car-

ried out on phase and charge qubits. The challenge

in performing accurate qubit operations lies in ef-

fectively isolating the two energy levels from the rest

of Hilbert space. In other words, how does one op-

erate as quickly, and with as little error as possible,

on the qubit subspace, while simultaneously isolat-

ing the remaining Hilbert space. This is especially

318 S.E. Shafranjuk and J.B. Ketterson

important when the coherence time of the system is

short.As an example, a Josephson phase qubit can be

described by three energy levels |0, |1,and|2,with

energies E

, E

,andE

. The qubit space is formed

by |0 and |1, and hence we wish to operate only

within this subspace. Clearly, the higher-order state

can be avoided when working in the |0,|1sub-space

provided the energies differ sufficiently and the ex-

citation pulse is long enough. However, because one

wants to maximize the number of logic operations

within a fixed coherence time, there is a need to mix

the |0 and |1 states as quickly as possible without

affecting other states.

Operations on charge qubits can be carried out

using the gate voltage alone. However much better

control is achieved using a hybrid qubit where the

charging and Josephson energies can be individually

controlled. Extensive experiments with this device

demonstrating controlled decoupling from the ex-

ternal environment are also described.

Section 9.4 describes a two-qubit gate involving

two capacitively coupled hybrid qubits and some as-

sociatedexperiments.Section 9.5 discusses a recently

proposed and promising two-qubit gate where the

qubitcoupling is engineered into a single device and

which is based on a multilayer SISIS junction.

Finally Sect. 9.6 discusses our conclusions where

we examine the outlook for Josephson-junction-

based quantum computing.

Although it is not the focus of this article, we

brieﬂy outline the elementary quantum logic oper-

ations that are necessary for performing quantum

computations in Appendix A.

Errors induced by the gate operations themselves

must be considered if fault-tolerant quantum com-

putation is to be achieved. The most obvious exam-

ple is ﬂuctuations in the control parameters of the

gate,which act as random noise and thus degrade the

unitarity of the time evolution of the computational

degrees of freedom.In addition,the actual gate oper-

ations can change the qubit coupling to the external

environment (even if the coupling is negligible dur-

ing storage periods) thereby enhancing decoherence.

Most sources of error can be analyzed by properly

modeling the qubit-environmentcoupling.However,

there are errors, which are not due to (or cannot be

described in terms of) the action of an external en-

vironment.An (intrinsic) source of error in gate op-

erations, [23] which is common to several of the pro-

posed solid-stateimplementations,is so-called quan-

tum leakage. Itoccurs when the computational space

is a subspace of a larger Hilbert space. The effects of

such states have been investigated for ion trap quan-

tum computers where estimates have been obtained

of the number of operations before decay processes

induce dissipative transitions outside the computa-

tional space [8].A procedure forestimating the leak-

age for a phase qubit will be given in Sect. 9.3.2.

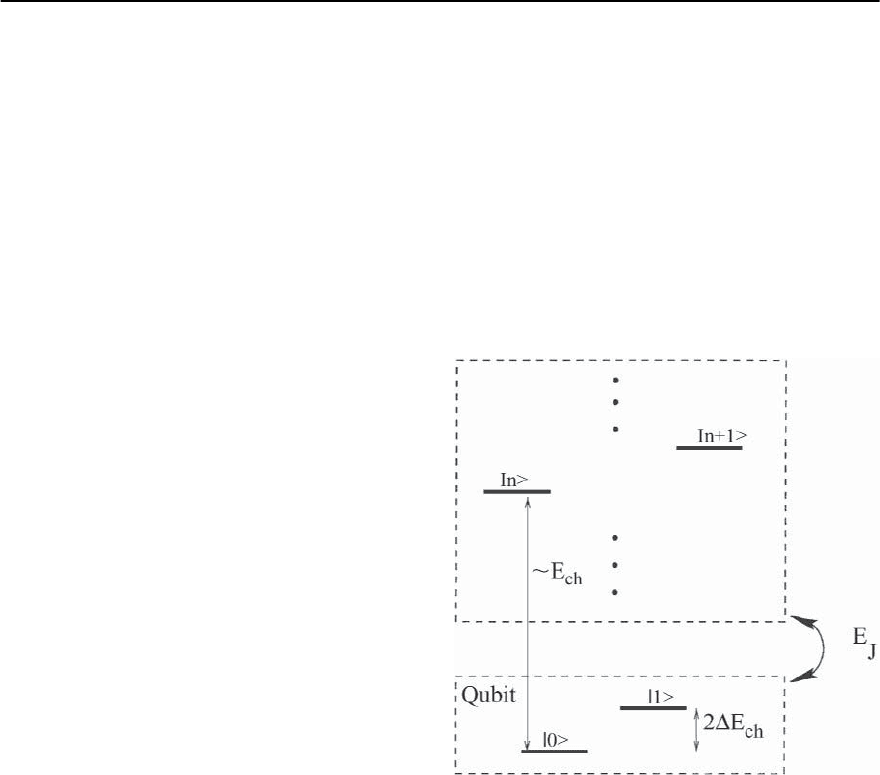
Fig. 9.3. Schematic view of a qubit with leakage (according

to [23]). The two low-energy states constitute the compu-

tational Hilbert space. The system, however, evolves under

the action of some unitary operator and can leak out to

the higher excited states. In the case of Josephson junc-

tion qubits, leakage is due to the Josephson tunneling to

higher charge states. In the case of two-qubit operations,

the computational space is spanned by the states |00, |01,

|10, |11 and the coupling with the higher charge states is

due both to E

and to inter-qubit coupling E

.Thetwolow-

energy states constitute the computational Hilbert space.

However the system can leak out to the higher states.If the

energy difference between the low-lying and the excited

states is large compared to the other energy scales of the

system, the probability to leak out is small