Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

298 V. Chandrasekhar

using the definition Eq. (8.127) of 1/.Ifwecon-

sider non-spin-ﬂip scattering alone, then ˆ can be

obtained by equating like terms in Eqs. (8.160) and

(8.162). If we include spin-ﬂip scattering, one can

write

ˆ

=−

2

ˆg

−−

2

ˆ

ˆg

ˆ

, (8.163)

as expected from Eqs. (8.133) and (8.134). For the

p-wave component, we consider only the contribu-

tion from non-spin-ﬂip impurity scattering, under

theassumption thatit is muchstrongerthan the spin-

ﬂip scattering.The second term under the integral in

Eq. (8.162) can be written as

−iN



d§



4

|v(

p ·



(

p ·



)ˆg



= (8.164)

−iN

ˆg



d§



4

|v(

p ·



[1 − (1 −

p ·



)] ,

where ˆg

can be taken out of the integral since it is

independent of the direction of p.Thefirsttermin

the square bracket can be seen to be related to the

elastic scattering rate 1/. The remaining terms can

be written in terms of the transport time, defined by



=2N



d§



4

|v(

p ·



(1 −

p ·



) , (8.165)

that is well known in the transport theory of metals.

With this definition, ˆ

canbewrittenas

ˆ

=−

(



−



)ˆg

. (8.166)

By putting Eq. (8.157) into the normalization condi-

tion for the quasiclassical Green’s function, and ne-

glectingterms quadratic in ˆg

,wealsoobtainthetwo

equations

ˆg

= 1 (8.167a)

and

ˆg

+ ˆg

ˆg

=0. (8.167b)

We now proceed to expand the Eilenberger equation,

Eq. (8.132), in terms of the s and p-wave expansions

of ˆg and ˆ . Replacing v

by v

p,weobtain

[ˆ

E −

, ˆg

p[ˆ

E −

, ˆg

] (8.168)

+ iv

p ·@

(ˆg

pˆg

)−[ˆ

, ˆg

]

−

p[ ˆ

, ˆg

]+[ˆ

, ˆg

p ·

p[ ˆ

, ˆg

]=0.

The last term is second order in the small quantity

ˆg

, and can be neglected. Collecting the terms that

are even in

p,weobtain

[ˆ

E +

, ˆg

]+iv

(

p ·

p)@

ˆg

=0. (8.169)

Averaging this equation over all directions of

p gives

[ˆ

E +

, ˆg

]+i

ˆg

=0. (8.170)

Ignoring spin-dependent scattering for the moment,

the terms that are odd in

p can be written

[ˆ

E +

, ˆg

]+iv

ˆg

−

2

[ˆg

, ˆg

]=0, (8.171)

where we have used Eqs. (8.163) and (8.166) to write

ˆ

and ˆ

in terms of ˆg

and ˆg

. If elastic scattering

is strong, the first term in the equation above can be

neglected compared to the third, so we obtain

ˆg



ˆg

=0, (8.172)

where we have used Eq. (8.167b) to simplify the sec-

ond term. Multiplying this equation by ˆg

on the left

and using Eq. (8.167a) we obtain

ˆg

=−



ˆg

, (8.173)

or writing ˆg

in terms of ˆg

we get

ˆg

= v



ˆg

=−ˆg

ˆg

. (8.174)

Here,we have introduced the elastic scattering length

 = v



. Putting this into Eq. (8.171) we obtain

[ˆ

E +

, ˆg

]−i



ˆg

=0. (8.175)

Writing this in terms of the diffusion coefficient

D =(1/3)v

, and reintroducing the spin-ﬂip scat-

tering term, we get

[ˆ

E +

 − ˆ

, ˆg

]−iD@

ˆg

=0. (8.176)

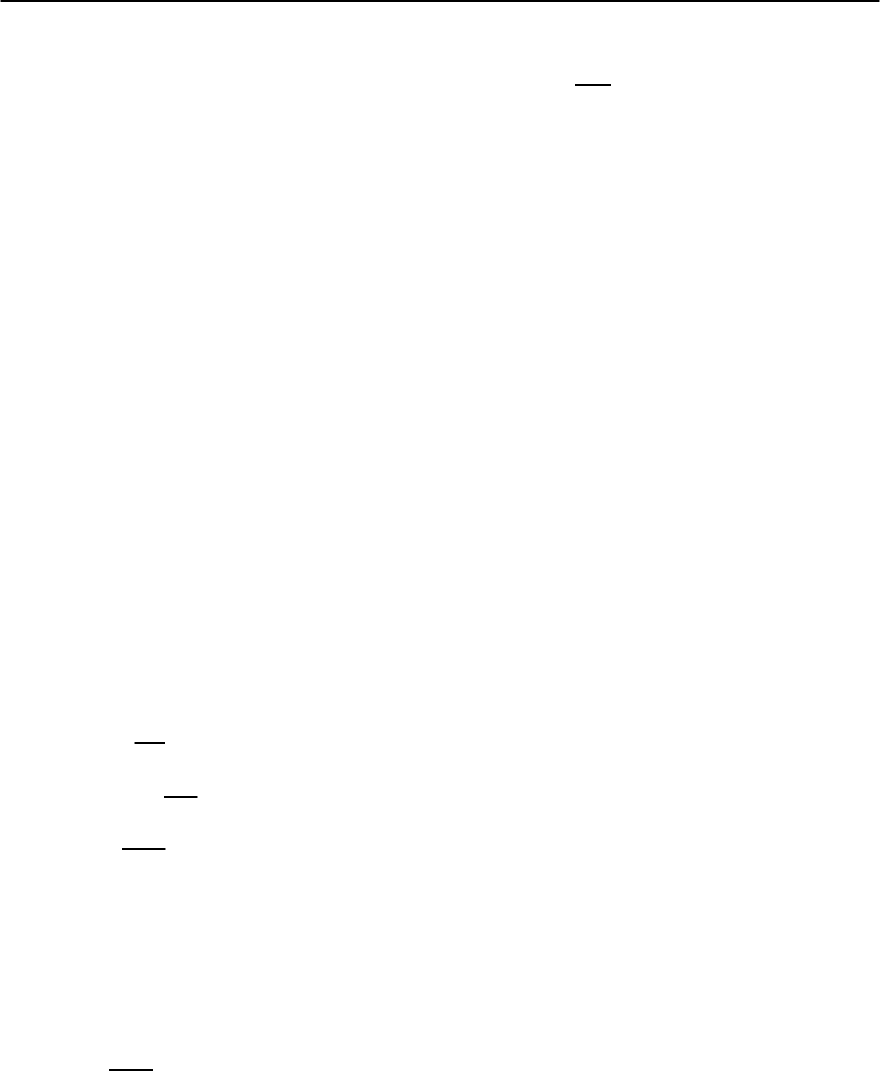
8 Quasiclassical Theory of Superconductivity 299

This is the equation first derived by Usadel [29] and

forms the starting point formost discussions of dirty

superconducting systems.

In the remainder of our development we shall ne-

glect the spin-ﬂip scattering term. Writing ˆg

as a

matrix

ˆg



˜g

0 ˜g



, (8.177)

we can write the matrix equation,Eq.(8.176),asthree

separate equations

[

E +

, ˜g

]=iD@

(˜g

˜g

) , (8.178a)

[

E +

, ˜g

]=iD@

(˜g

˜g

) , (8.178b)

and

[

E +

, ˜g

]=iD@



(˜g

˜g

)+(˜g

˜g

)



(8.178c)

As before, the first two equations come from the di-

agonal components of the Usadel equation, and de-

scribe the equilibrium properties of the system,while

the third equation comes from the off-diagonal or

Keldysh component,and represents the kinetic equa-

tion for the distribution function. These equations

are supplemented by the equations for measurable

quantities corresponding to Eqs.(8.138),(8.139) and

(8.138).Expanding ˜g

inEq.(8.138 using Eqs.(8.157)

and (8.138), we have

j(R, T)=−



dE (8.179)



d§

4

pTr







˜g

p˜g





dETr





(˜g

˜g

)



where the angular average over the p-wave compo-

nent gives a factor of (1/3), and we have replaced

(1/3)v

 by the diffusion coefficient D.Now

(˜g

˜g

)

=(˜g

˜g

)+(˜g

˜g

) (8.180)

so that Eq. (8.180) above can be rewritten as

j(R, T)=

(8.181)



dETr







˜g

+ ˜g

˜g



The equation for j

is obtained in a similar way

(R, T)=

(8.182)



dEETr



˜g

+ ˜g

˜g



The kinetic equation, Eq. (8.178c), can be recast

in terms of a differential equation for a distribution

function

h,in the hopesof separating the equilibrium

properties of the system, represented by ˜g

and ˜g

from the non-equilibrium properties of the system,

represented by

h.Tothisend,asbefore,wesubstitute

Eq.(8.143)for ˜g

inEq.(8.178c),which thenbecomes

[

E +

, ˜g

h]−[

E +

,

h˜g

iD@



˜g

)

h −

h˜g

˜g

)



+ @

h −



˜g

h˜g



. (8.183)

Taking the trace of both sides of the equation above

gives

0=iD@



h + ˜g

˜g

)

−

h˜g

˜g

)−˜g

h)˜g



, (8.184)

using Eqs.(8.178a) and (8.178b).Inthe linear regime,

we can use the diagonal representation of

h given by

Eq. (8.146) to obtain



)Tr



1−˜g

˜g



+ h







˜g

)−˜g

˜g

)





−(@

)Tr



˜g



˜g



=0. (8.185)

Here,wehaveusedthefactthat

(˜g

˜g

)

=Tr

(˜g

)˜g

+ ˜g

(˜g

)

=2Tr

˜g

(˜g

)

=0. (8.186)

Taking the trace after multiplying both sides of

Eq. (8.183) by 

gives



1−˜g



˜g



(8.187)

+ h





˜g

)−˜g

˜g

)

>

− @

˜g



>





[˜g

− ˜g

]

−2h

(˜g

+ ˜g

)



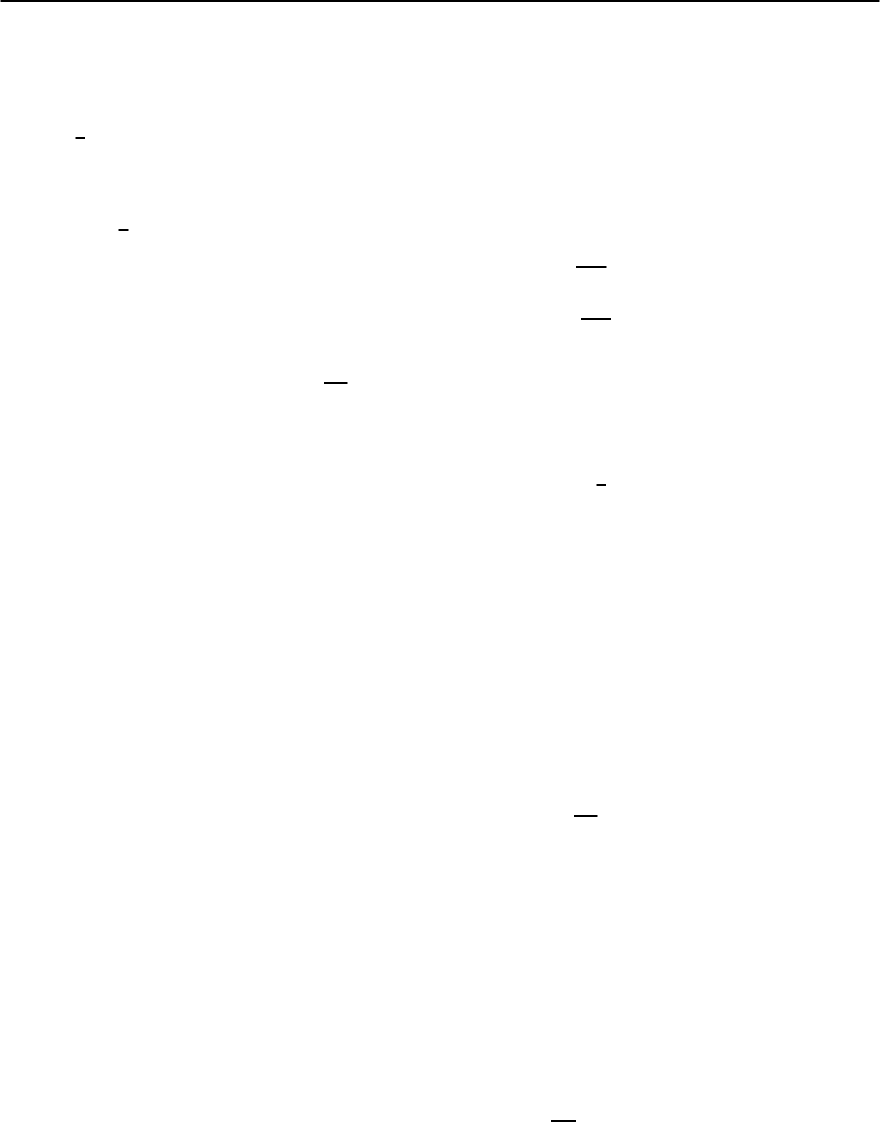
300 V. Chandrasekhar

Equations (8.185) and (8.188) form a set of coupled

differential equations for the distribution functions

and h

. Let us define the quantities

Q =





˜g

)−˜g

˜g

)

>

(8.188)

and



− ˜g



˜g



. (8.189)

Then Eqs. (8.185) and (8.188) can be written in the

form

[

)+Qh

+ M

)

]

=0, (8.190a)

[

)+Qh

+ M

)

]





[˜g

− ˜g

]

−2h

(˜g

+ ˜g

)



. (8.190b)

These equations are in the form of diffusion equa-

tions for the distribution function, more general

forms of the diffusion equation discussed for the

normal case in the introduction. As we shall see, the

quantity Q is related to the spectral supercurrent in

the system, DM

are now the energy and position

dependent diffusion coefficients, and Eq. (8.190) are

essentially continuity equations for the spectral ther-

mal and electric current.In the normal limit,g

= 

=−

,and

 =0,sothatM

= M

=1,and

Q = M

= M

= 0. Equations (8.190) then re-

duce to Eq. (8.1), as expected. Noting that the term

in square brackets in Eq. (8.178c) is the same as the

term in parenthesis in Eq. (8.182) and the term in

square brackets in Eq. (8.183), the electric current

can be written as

j(R, T)=eN

D (8.191)



dE (M

)+Qh

+ M

) .

The first term corresponds to quasiparticle (or dis-

sipative) current, and the second term to the super-

current. The third term, which is proportional to the

derivative of h

, is associated with an imbalance be-

tween particles and holes. The thermal current can

be written in a similar way

(R, T)=N

D (8.192)



dEE[M

)+Qh

+ M

] .

For the charge-imbalance Q

∗

, we note that only the

s-wave part of the Keldysh Green’s function in the

square brackets in Eq. (8.139) survives after an-

gular averaging. Writing g

in the form given by

Eq. (8.143), with

h given by Eq. (8.146), we have

∗

=−



dEh

− g

−



dEh



− g

)

=−eN



dEh

N(E) , (8.193)

since g

and g

are traceless. Here we have defined

the normalized superconducting density of states by

N(E)=



− g

)

, (8.194)

which reduces to the conventional BCS density of

states in the equilibriumcase.

We canalsorecast thekineticequationsEq.(8.190)

in a slightly different form sometimes used in the lit-

erature. To do this, we subtract Eq. (8.178b) from

Eq. (8.178a), multiply by 

, and take the trace. The

result is



− g

]

=−iD@

(Tr



[˜g

˜g

− ˜g

˜g

]

) . (8.195)

Using the definition of Q,wehave

Q =



− g

]

. (8.196)

If we choose a gauge in which  is real, the right

hand side of the equation vanishes, so that @

Q =0.

Clearly, @

Q = 0 also for a normal metal (even a

proximity-coupled normal metal),where  vanishes.

In either case, the spectral supercurrent Q is con-

served. The right hand side of the equation above

multiplied by h

isthesameasthesecondtermof

Eq.(8.190b).Subtracting Eq.(8.195) multiplied byh

from Eq. (8.190b), we obtain

[

)+M

)

]

+ Q(@

−



(˜g

+ ˜g

)



. (8.197)

8 Quasiclassical Theory of Superconductivity 301

For real ,when@

Q = 0, Eq.(8.190a) can be written

in a similar manner

[

)+M

)

]

+ Q(@

)=0. (8.198)

Finally, we can also write the kinetic equations in a

form similar to Eq. (8.150)

˜g

h]−B[

h]˜g

=0, (8.199)

by performing similar manipulations on Eq. (8.178)

as were performed on Eq. (8.148). For the diffusive

case, B[

h] is a functional of

h now given by

h]=[

E +

,

h]−iD



˜g

)(@



˜g

h)−(@

h)˜g



(8.200)

−(@

h)(@

˜g

)



Boundary Conditions for the Quasiclassical Equ ations

of Motion

Equation (8.178) or their derivatives form a set of

coupled differential equations for the quasiclassical

Green’s functions and the distribution function. In

order to obtain a solution, however, we need to spec-

ify the boundaryconditionsfor the Green’s functions

and the distribution function.To this end, we define

the concept of a reservoir, where the Green’s func-

tions and distribution function have well-defined

values.

For a normal reservoir, the retarded and advanced

quasiclassical Green’s functions are given by

= 

; g

=−

, (8.201)

and for the superconducting case, by Eq. (8.155),

which we reproduce here

˜g

⎛

⎜

⎝



− ||





− ||

−



∗



− ||

−



− ||

⎞

⎟

⎠

, (8.202)

with g

is given by Eq. (8.156).

The equilibrium distribution function

h is given

by Eq. (8.121) in both normal and superconduct-

ing reservoirs (since we are dealing only with ex-

citations), where, as we noted earlier the (1, 1) com-

ponent of the matrix applies to particle-like excita-

tions,and the (2, 2) component of the matrix applies

to hole-like excitations. From this point of view, the

Fermi functions in Eq. (8.121) are given in terms of

the usual equilibrium Fermi function Eq. (8.5) by

0↑

(E)=f

(E)andf

0↓

(E)=f

(−E). (Since we are

dealing with the static limit in all that follows, we

again use the symbol T to refer to the temperature.)

Looking ahead to where we might have a finite volt-

age V on a reservoir, the equilibrium form of

h can

then be written as

⎛

⎜

⎝

tanh



E + eV



0tanh



E − eV



⎞

⎟

⎠

. (8.203)

If we write

in the form of Eq. (8.146) the equi-

librium values of h

and h

can then be expressed

L,T



tanh



E + eV



±tanh



E − eV



(8.204)

If afinitevoltageis putonthesuperconductor,wewill

obtain a time evolution of the phase in accordance

with the Josephson relations.Since we have restricted

ourselves here to the static case,we must assume that

the voltage on the superconducting reservoir V =0.

In this case,h

= 0 for the superconducting reservoir.

For a system with perfect interfaces between the

superconducting and normal parts, the boundary

conditions defined by the equations above are suf-

ficient to solve the differential equations,the implicit

assumption being that the Green’s functions and the

distribution functions are continuous across any in-

terface.When the transparency of the interface isless

than unity,thisis no longer true.Zaitsev [30] derived

the boundary conditions for the Green’s functions at

an interface of arbitrary transparency. Kupriyanov

and Lukichev [31] simplified these equations for the

diffusive case in the limit of small barrier trans-

parency. Consider then an interface at x = 0 between

302 V. Chandrasekhar

two metals, say one a normal metal in the half-plane

x < 0 (labeled by the index ‘1’) and one a super-

conductor in the half-plane x > 0, (labeled by the

index ‘2’), although it also could be an interface be-

tween two different normal metals or superconduc-

tors. The boundary conditions of Kupriyanov and

Lukichev are then

ˆg

)=v

ˆg

) , (8.205a)

ˆg

[ˆg

, ˆg

] . (8.205b)

Here @

denotes a derivative in the positive x direc-

tion,and r = R

is a parameter that is nominally

the ratio of the barrier resistance R

to the normal

wire resistance per unit length R

/L,but is inversely

proportional to the transmission t of the interface.

The firstof the equations is clearly related tothe con-

servation of current across the interface. The right

hand side of the second equation has been shown

to be the first term in an expansion of terms of the

transmission coefficient t [14], and hence, it is only

valid for low t.

The diagonal part of Eq.(8.205b) gives the bound-

ary condition for the Green’s functions

˜g



˜g

− ˜g

˜g



. (8.206)

The off-diagonal part of Eq. (8.205b) gives the

boundary condition for the distribution function

˜g

+ ˜g

˜g



˜g

+ ˜g

˜g

− ˜g

˜g

− ˜g

˜g



(8.207)

If we put in Eq. (8.143) for ˜g

, with Eq. (8.146) for

h, and then take as before the trace of the resulting

equation, and the trace of the equation multiplied by



,we will obtain boundary conditions for h

and h

Noting that the left hand side of Eq.(8.207) is simply

the term in square brackets on the right hand side of

Eq. (8.178c), we obtain the two equations

[

)+Qh

+ M

)

]

= ˛

, (8.208a)

and

[

)+Qh

+ M

)

]

= ˛

, (8.208b)

where

=Tr

˜g

(˜g

−

˜g

)+(˜g

−

˜g

)˜g

− ˜g

(˜g

−

˜g

)−(˜g

−

˜g

)˜g

, (8.208c)

and

=Tr

(

˜g

(˜g

−

˜g

)+(˜g

−

˜g

)˜g

− ˜g

(˜g

−

˜g

)−(˜g

−

˜g

)˜g

)

. (8.208d)

We note that although the boundary conditions of

Kupriyanov and Lukichev are valid for large r,they

also give the correct boundary conditions (that of

continuity of the Green’s functions and distribution

functions) in the limit of r → 0. For arbitrary trans-

mission of a barrier with n channels, the boundary

condition can be represented as [19]

ˆg

=





[ˆg

, ˆg

]

4+T

(ˆg

ˆg

+ˆg

ˆg

−2)

(8.209)

where  is a constant factor, and T

is the transmis-

sion of the nth channel.It can be seen that for a single

channel with small transmission T,thisequationre-

duces to the boundary condition of Kupriyanov and

Lukichev.

8.8 Parametrization of the Quasiclassical

Green’s Function

The normalization Eq. (8.167a) permits a parame-

trization of the quasiclassical Green’s functions that

is very convenient forcalculations.Equation(8.167a)

isamatrixequationthatisequivalenttothethree

equations (8.142) for the s-wave component of the

Green’s function. To take into account the macro-

scopic phase of the superconductor, we note that a

gauge transformation that transformsthe vector and

scalar potentials according to Eqs. (8.93) and (8.94)

transformsthe fieldoperators accordingto the equa-

tions

ˆ →ˆ e

i

, (8.210a)

→ˆ

−i

. (8.210b)

The Nambu–Gor’kov Green’s functions defined in

Eq.(8.109) aretransformedaccordingly.Forexample,

8 Quasiclassical Theory of Superconductivity 303

two components of

ˇ˛

would transform according

[

ˇ˛

]

→ [

ˇ˛

]

−i

(

(r

)−(r

)

, (8.211a)

[

ˇ˛

]

→ [

ˇ˛

]

(

(r

)+(r

)

. (8.211b)

Making the transformation (8.42a) to mixed coor-

dinates, and taking the limit as r → 0, we see that

the off-diagonal components of the Nambu–Gor’kov

Green’s functions are multiplied by a phase factor

i(R)

or e

−i(R)

, while the diagonal components re-

main unchanged.Consequently, also transforms as

 → e

i(R)

. (8.212)

Keeping this in mind, we can express ˜g

˜g



cosh sinh e

i

−sinhe

−i

−cosh



, (8.213)

where  and  are complex functions of the energy E

and position R.This form satisfiesthe normalization

condition ˆg

ˆg

= 

. Note, one can also express ˆg

equivalently in terms of sin and cos. For complete-

ness, we also give the expression for ˜g

˜g



−cosh

∗

−sinh

∗

i

∗

sinh 

∗

−i

∗

cosh 

∗



. (8.214)

We now put this into the Usadel equation for ˜g

Eq. (8.178a). Keeping in mind that the matrix for



involves additional factors of e

i

and e

−i

due to the

gauge transformation, the diagonal (1,1) component

of this matrix equation is

D sinh

@

 + D sinh 2@

@



−2iIm()sinh =0, (8.215a)

and the off-diagonal component (1,2) is

 −

sinh 2 (@

)

+2Ei sinh 

−2iRe()cosh =0, (8.215b)

where we have used Eq. (8.215a) to simplify

Eq.(8.215b). Defining a current j

(E, R)bytheequa-

tion

(E, R)=sinh

(E, R)@

(E, R) , (8.216)

we can rewrite Eq. (8.215a) as

(E, R)−2iIm()sinh =0. (8.217)

(E, R) is proportional to sinh

, which is propor-

tional to the square of the pair amplitude, and it is

also proportional to the gauge-invariant gradient of

the phase. Consequently, it is similar in form to the

conventional definition of the supercurrent, and is

called the spectral supercurrent. Indeed, Eq. (8.217)

is simply another way of writing Eq. (8.196), and Q

and j

are related by

Q(E , R)=−Im(j

(E, R)) . (8.218)

As we noted before, @

Q =0if is purely real, and

from Eq. (8.217), it can be seen that @

(E, R)=0

also if  is real.

Equations(8.215) form a set of coupled equa-

tions that can be solved in principle for (E, R)and

(E, R).Inthecaseofanegligiblespectralsuper-

current, the equations decouple, and one needs to

solve only Eq. (8.215b). In the limit of a bulk super-

conductor with a uniform real order parameter and

no phase gradient, we recover the bulk value of the

Green’s function, Eq. (8.155). The differential equa-

tions must be supplemented by boundary conditions.

From Eq. (8.155),in a superconducting reservoir, we

have

cosh 



− ||

, (8.219)

so that the value of  in the superconducting reser-

voir is given by



⎧

⎪

⎨

⎪

⎩

−i



|| + E

|| − E

if E < || ,

E + ||

E − ||

if E > ||.

(8.220)

The value of  in a superconducting reservoir is just

the macroscopic phase of the superconductor. In a

normal reservoir,  =0.Thevalueof in a normal

reservoir is meaningless, of course, and any choice

that results in no phase gradient is valid.

In terms of the  parametrization, the boundary

conditions of Kupriyanov and Lukichev can be ex-

pressed as

r sinh 



)=sinh

sin(

− 

), (8.221a)

304 V. Chandrasekhar

and





+ i sinh 

cosh 



)



= (8.221b)

cosh 

sinh 

i(

−

)

−sinh

cosh 

Note, that for r = 0, the boundary conditions reduce

to 

= 

and 

= 

. In the absence of a supercur-

rent, (@



) = 0,so that the equations above simplify



= 

, (8.222a)

and

r(@



)=sinh(

− 

) . (8.222b)

Finally, we can write expressions for physical quan-

tities in terms of  and . These quantities can be

written in terms of the M



1+cosh cosh 

∗

−sinh sinh 

∗

cosh(2Im())



, (8.223a)



1+cosh cosh 

∗

+sinh sinh 

∗

cosh(2Im())



, (8.223b)

=−

sinh  sinh 

∗

sinh(2Im()), (8.223c)

and

sinh  sinh 

∗

sinh(2Im()) . (8.223d)

If  is real, then the M

= M

=0,andM

and M

simplify to

=cos

(Im()) (8.224a)

and

=cosh

(Re()) . (8.224b)

These relations will be used in the next section when

we discuss applying the Usadel equation to derive the

transport properties of some simple device geome-

tries.

To conclude this section, we shall write an expres-

sion for the gap in terms . Replacing Eq. (8.143) for

˜g

into Eq. (8.137) for the gap, we have

 = N





dE [˜g

h −

h˜g

]

, (8.225)

where performing the angular average in Eq. (8.137)

gives the s-components of the Green’s functions.

Putting in

h in the form of Eq. (8.146), we obtain

 = N





dE [h

(˜g

− ˜g

)+h

(˜g



− 

˜g

)]

(8.226)

With ˜g

and ˜g

given by Eqs. (8.213) and (8.214),we

obtain

 = N







(sinh e

i

+sinh

∗

i

∗

) (8.227)

− h

(sinh e

i

−sinh

∗

i

∗

)



As an example, consider the case of a bulk supercon-

ductor, where  =0andh

=0.Wethenhave

 = N





dEh

Re(sinh ) (8.228)



∞



dE tanh(E/2k

T)Re





√

−



which is the usual self-consistent equation for the

gap.

8.9 Applications of the Quasiclassical

Equations to Proximity-Coupled Systems

We shall conclude our discussion of the quasiclas-

sical theory by applying the equations that we have

derived to some simple devices incorporating nor-

mal metals in close proximity with superconductors.

Since the equations of motion in the diffusive limit

are in general nonlinear, solving them usually re-

quires numerical techniques, except in the limit of

large resistances between the superconductor and

the normal metal, where the Usadel equation can

be linearized. We shall restrict ourselves to one-

dimensional examples; these are the ones discussed

most in the literature.

8 Quasiclassical Theory of Superconductivity 305

8.9.1 Proximity-Coupled Wire

We start with the simplest possible device, a one-

dimensional normal-metal wire of length L con-

nected on one end to a superconducting reservoir

and at the other end to a normal metal reservoir.For

definitiveness,let us take the superconducting reser-

voir to be at x = 0 and the normal-metal reservoir at

x = L, and let us consider first the case of a perfect

SN interface, so that the interface barrier resistance

parameter r = 0. In this geometry, there can be no

supercurrent, so that Q (or alternatively, j

)iszero.

Furthermore, we can take the phase  to be zero in

the superconducting reservoir without loss of gen-

erality, and we note again that  =0inthenormal

metal. Under these conditions, only M

and M

are

non-zero in Eq. (8.190), which now read

)=K

, (8.229a)

and

)=K

, (8.229b)

where K

and K

are constants of integration. On in-

tegrating these equations from x =0tox = L,we

obtain

(x = L)−h

(x =0)=K



dx , (8.230a)

(x = L)−h

(x =0)=K



dx . (8.230b)

To calculate the conductance of the normal-metal

wire in the linear approximation, we apply a small

voltage V on the normal-metal reservoir, keeping the

superconducting reservoir at V =0.Ifweconsider

the second equation, h

(x = 0) = 0, and expanding

(x = L) in a Taylor’s expansion to first order, we

obtain from Eq. (8.230b)

T cosh





⎡

⎣



(E, x)

⎤

⎦

−1

(8.231)

The electric current in the linear response regime

can then be obtained from Eq. (8.192)

j =

(8.232)



cosh

(E/2k

⎡

⎣



(E, x)

⎤

⎦

−1

There are two differences between this equation and

the equivalent equation for a normal metal in the

classical regime (Eq. (8.10a)) that we derived earlier.

First, the equation above involves an integral over

energy and position. One can define a energy and

position dependent electrical diffusion coefficient

(E, x)=DM

(E, x) (8.233)

instead of the constant diffusion coefficient D in

Eq. (8.10a). Second, the current in Eq. (8.233) does

not involve temperature differentials. Indeed, if one

assumes that the superconducting reservoir is at a

temperature T, and the normal reservoir at a tem-

perature T + T, and expand h

(x = L)tofirstorder

in T,thetermsinvolvingT cancel, so that there

is no term proportional to T. As a consequence,

thermoelectric phenomena cannot be described us-

ing the quasiclassical equations, and an extension to

thetheoryisrequiredtotakethemintoaccount.

From Eq. (8.233),one can define a spectral or en-

ergy dependent conductance of the wire

G(E)=G

⎡

⎣



(E, x)

⎤

⎦

−1

, (8.234)

whereG

is thenormal state conductanceof the wire.

The total conductance is then

G =



G(E)

T cosh

(E/2k

. (8.235)

Figure 8.4 shows the results of a numerical calcu-

lation of G(E)/G

as a function of the normalized

energy E/E

. The normalization factor E

= D/L

is called the correlation energy or Thouless energy

(from the theory of disordered metals, where it also

occurs) [32], and is dependent on the length L of

See, for example, F. Wilhelm, PhD Thesis, Universit¨at Karlsruhe,2000.

306 V. Chandrasekhar

Fig. 8.4. Spectral conductance G(E) of a one-dimensional

wire of length L as a function of energy E,normalizedto

the correlation energy E

. The barrier interface parameter

r=0, and the gap is set to be  = 1000E

Fig. 8.5. Temperature dependent resistance R(T)normal-

ized to the normal state resistance R

,asafunctionof

the temperature T normalized to E

, for different values of

the interface resistance parameter r.Thegapissettobe

 =32E

the wire. At high energies, G(E) approaches its nor-

mal state value, as expected.As the energy is lowered,

the conductance increases, as might be expected in

a proximity-coupled normal metal. However, instead

of continually increasing as the energy is reduced,

it reaches a maximum of around 1.15 G

at an en-

ergy of E  5E

, and then decreases, reaching its

normal state value at E = 0. This non-monotonic be-

havior of the conductance is called reentrance, and

has been observed in experiments by a number of

groups [33].Itshould be emphasized that the relevant

energy scale where the maximum in conductance is

observed is set not by the gap  of the superconduc-

tor, but by E

, which itself depends inversely on the

square of the length of the sample L.Henceinvery

long or macroscopic samples,the energy (and corre-

spondingly, the temperature) at which the minimum

would occur is far below the experimentally accessi-

blerange,andoneregainsthemonotonicbehavior

expected from the simple Ginzburg–Landau theory

of de Gennes [34].

The temperature dependent conductance G(T)

can be obtained from G(E) using Eq. (8.235); the re-

sult of this calculation, plotted in terms of the nor-

malized resistance R (T)/R

, is shown in Fig. 8.5. In

obtaining this plot,we have used a value of  =32E

corresponding to a weak-coupling transition tem-

perature of T

=1.764/k

, typical parameters for

Al films. We have also assumed that the gap is tem-

perature dependent. Like G(E ), R(T)isalsonon-

monotonic, with a minimum at some intermediate

temperature.We would expect the minimum in R(T)

to be around T  5E

, based on the behavior

of G(E). However, the temperature dependence of

the superconducting gap modifies this behavior, so

that the minimum in resistance occurs at a some-

what higher temperature when the interface between

the normal metal and the superconductor is perfect.

Figure 8.5 shows additional curves corresponding to

progressively increasing values of the interface bar-

rier parameter r. Increasing the resistance of the NS

interface decreases the leakage of superconducting

correlations from the superconductor into the nor-

mal metal, and consequently results in a smaller in-

crease in the conductance of the proximity-coupled

normal metal. In addition, the temperature T

min

8 Quasiclassical Theory of Superconductivity 307

Fig. 8.6. Density of states N(E, X) normalized to the nor-

mal state density of states N

for a one-dimensional wire

of length L,asafunctionofE/E

and position x along the

wire. The superconducting reservoir is at x =1.0, and the

normal reservoir is at x = 0. The density of states is sup-

pressed at low energies near the superconducting reservoir

which the minimum in resistance occurs is also

shifted down.

From Eq.(8.194),the normalized density of states

N(E) can be expressed in terms of  as

N(E)=cosh

(

Re()

)

cos

(

Im()

)

. (8.236)

Figure 8.6 shows the density of states as a function of

energy and position along the wireof length L.There

is a proximity-induced decrease of N(E)nearthesu-

perconducting reservoir. In fact, at the NS interface,

there is a divergence in N(E) at the gap energy, and

it goes to zero at E = 0, just as one would expect for

a superconductor. However, unlike a superconduc-

tor, it is not strictly zero for E < ,butstillhasa

finite amplitude. As one moves away from the NS in-

terfaceinto the proximity-coupled normal wire,both

the amplitude of this effective gap and the divergence

are smoothly reduced,so that at the normal reservoir,

one recovers the normal density of states. This posi-

tion dependent variation of the density of states has

been observed in experiments [35].

In our analysis above of the proximity effect in a

normal metal coupled to a superconductor,we have

ignored the effects of electron decoherence on the

proximity correction.Phase coherence is essential to

observing the proximity effect; if the phase coher-

ence length L



is less than the length of the sample

L, a finite spatial cutoff of the proximity effect is in-

troduced.Phenomenologically,this can be taken into

account by saying that the length of the wire is now



instead of L.SinceL



is typically of the order of

a few microns even at low temperatures, this sets the

dimensions of the samples that are required to ob-

serve this mesoscopic proximity effect.

While L



sets the upper cutoff for observing the

proximity effect, a second relevant length scale for

the problem can be obtained by considering the

length at which E

is equal to k

T.Thislengthis



D

, (8.237)

where L

is called variously the thermal diffusion

length or the Thouless length, again from the theory

of disordered metals, where it also occurs [32]. (We

put in here explicitly the factor of .) In fact, here it

is simply the diffusive form of the superconducting

coherence length in the normal metal, familiar from

the de Gennes/Ginzburg–Landau theory of the prox-

imity effect [34], which in the clean limit is given by



v

. (8.238)

At low temperatures, when L

is longer than L,the

superconducting correlations induced in the normal

metal extend throughout its length. At higher tem-

peratures, they are restricted to a region of length L

near the superconductor. L

is also on the order of

a few microns in typical metallic samples in acces-

sible temperature regimes, so it also sets a limit on

the dimensions of the samples in which one can see

a proximity effect.

To calculate the thermal conductance of the wire,

we proceed from Eq. (8.230a). We now consider a

small temperature differential T applied across the

wire. Expanding h

in a first-order Taylor’s expan-

sion, as we did for h

,weobtain