Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

where S

' = {j€ TL

/ \y\ = 1}. Since S

N 1

is compact there exists y* € S

N 1

such

that

From (2.8) one has

We claim that

Indeed assume that

inf

yes"-'

Wi •

V = V Wfy*

i=-l i=-\

-y*>0.

Wi •

> 0.

•

(2.10)

Then

Vi = -l,0,...,fc u;i-y* < 0,

but from (2.8) one has

J2 frv>i

•

= o,

(o,

l).

Then

Wi- y" =0 Vi = 1,.. .,fc

and (2.7) implies that y* = 0 which contradicts the fact that y* 6 S^"

. Thus (2.10)

holds and

N^-r-^ Vies.

Vi=-i

i ' 2/

Therefore 5 is a bounded open set. Taking 0 = 5, one has

u € Wo

(ft).

Since the ujj's belong to W($) and u verifies (2.9) we deduce that it is a minimizer of the

minimization problem (1.6) with

= S. Then one can construct a minimizer on Q by

covering it with scaled copies of 5 using Vitali's covering lemma.

In the absence of minimizers we turn to the study of minimizing sequences. We will follow

the ideas in [C.C.] taking now into account of the data of our problem. Namely we will

use the fact that a Lipschitz function vanishing at the boundary and verifying (2.3) is

identically equal to 0. Then we have

Theorem 2. Assume that

W{<p)

C B+.

Let (u„)„ be a minimizing sequence of (1.6) such that

\\u

{x)\\,

||Vw

(z)|| <C a.e. in U (2.11)

for some constant C independent of n

(\\-\\

denotes a norm in R or K

), then one has

—y 0 uniformly in fi

Proof.

From (2.11), by a compactness argument there exist u G

WQ'°°(Q)

and a subse-

quence u

such that

u„,

—•

u uniformly in Q

->• Vu in L°°{Q)

- * weak (2.12)

when k

—¥

oo. Now, the bounded sequence of gradients generates a Young measure on

R" (see [P.]) in the sense that there is a probability measure v

on R

and a subsequence

of Vu

-still labeled

Vu„

such that for any continuous function F on ~R

one has

F{Vu

) -± f F{X)dv

(X) in L°°(Q) - * weak. (2.13)

JR."

3) with F =

and since (u

)

is a minimizin

f 1

•

<p(Vu

J —> 0 = f [ ip(X) dv

{\)dx

Jn JSIJR"

/R"

Considering first (2.13) with F =

and since (u

)

is a minimizing sequence one gets

It follows that

<p(X)

(X] = 0 a.e. in fi

/R"

One deduces that

Supply C W(p) C B+, for a.e. i£f! (2.14)

where Supply denotes the support of v

. Considering then for F in (2.13) the function

F(X) =

A •

Combining this with (2.12) one deduces that

(x)

• M

-*• / ^

•

(\) in L°°(n) - * weak.

12) one deduces that

Vu(i)

• M

= /

A •

fi dv

{\) a.e. in Q, (2-15)

but by (2.14) one has

/ X-n dv

(X) > 0 a.e. in Q. (2.16)

JR"

Combining (2.15), (2.16) and (2.4) one deduces that u = 0. Since the sequence has 0 as

unique limit point the whole sequence converges towards 0. One has finally obtained

u„

—•

0 uniformly in Q

Vu„

->•

0 in L°°(Q)

- * weak (2.17)

This completes the proof of theorem 2.

•

In the following theorem we express the behaviour of the minimizing sequences in terms of

Young measure. As we will see, they have a precise pattern governed only by the N wells

Wi and the boundary condition. More precisely we have

Theorem 3. We assume that

WW C H+.

If (u„) is a minimizing sequence of problem (1.6) satisfying (2.11) then

—>

0 uniformly in Q. (2-18)

Moreover the sequence of gradients

VM„

generates a unique homogeneous Young measure

on R

given by

»>i

(2.19)

i=l

where S

denotes the Dirac mass at the point

and the

cti

's are the constants appearing

(1.8).

Proof.

The assertion (2.18) is a simple consequence of theorem 2. Let

)

X€

be the

Young measure associated to Vu

verifying (2.13). Combining (2.13) and (2.17) one

obtains

A •

fj,

{\) = 0 a.e. in fl. (2.20)

Due to (2.20) and the fact that

Suppi^ C

W(<p)

and

W(<p)*

C H

one deduces that

Suppv

{uii,

i = 1,..., N}

so that there exist N measurable functions

j3i

X^<w

(

)

i=l

Since v

is a probability one has

$^ft = l, ft>0. (2.22)

i=l

Let B be a ball included in Q. From (2.13) applied to F(X) = \ and (2.17) we obtain

/ / A dv

{\)dx = 0.

JBJK

By (2.21) this reads

ax • W{.

(2.23)

,N.

)

,=I

Hence by (1.8), (2.22) and (2.23) one has

-- / pi(x)dx = a

{

Vi = 1,

Since this is true for any ball B, it comes out that

j5i(x) = oti(x) a.e. in Q, Vi = 1,..., iV

and thus (2.21) reads

= 2_,

i&wi a.e. in fi.

This shows that v

is necessarily the homogeneous Young measure in (2.19)

Remark 1. If W{ip)* n H is not empty, then the bounded minimizing sequences of (1.6)

converge toward 0 (cf Theorem 2) but they may not generate the same homogeneous

Young measure. Indeed when we have wells satisfying (1.8) one can construct a minimiz-

ing sequence of the minimization problem (1.6) satisfying (2.11) and whose sequence of

gradients generates a Young measure given by (2.19) (see [C.]).

Let us illustrate our results by the following example

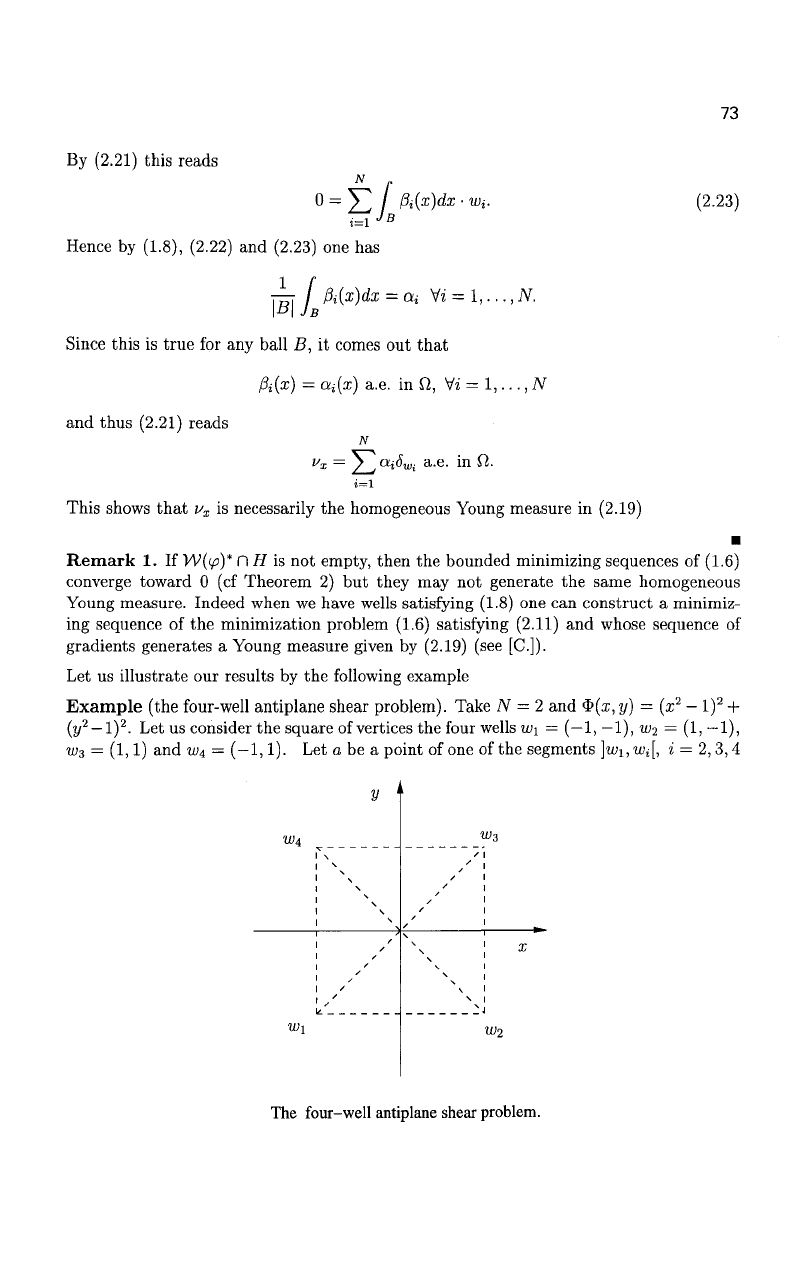
Example (the four-well antiplane shear problem). Take

= 2 and $(x, y) = (x

—

Let us consider the square of vertices the four wells «Ji =

(—1,

—1),

(1,

—1),

= (1,1) and

u>4

= (-1,1). Let a be a point of one of the segments

]u>i,Wi[,

i = 2,3,4

•

1 \

. \

I \

1 s

•

l /

1 /•

1 /

/ 1

\ 1

! x

\ 1

The four-well antiplane shear problem.

]w2,

uii[,

i = 3,4 or ]w

,u>4[ and consider the minimization problem (1.6) with the

boundary condition u(x) = a

•

x on T. If a belongs to the diagonals ]wi, »3[ or ]u>

,u>4[

one can immediately conclude that the problem in hand attains its infimum. Indeed for

example if a e]wi, w

[ then the two other wells w

and w\ are respectively in the two

half-

spaces separeted by the straight line passing by the wells w\ and w

. Now if a belongs to

one of the sides of the square for instance a €]wi, w

[ then the other wells are all in one of

the half-spaces determined by the straight line passing by the wells w

and w

. One can

conclude that the minimization problem does not admit minimizers. So we have studied

this problem, considering special boundary conditions, without computing the convex

envelope of $(z, y) = (x

- l)

+ (y

- l)

. Notice that if a belongs to the interior of the

square of vertices W\, w

, u>3 and UI4, one can also conclude that the problem (1.6) admit

minimizers using the second part of the proof of theorem 1. Now if a e {i«i, w

W3,

one can easily see that the Lipschitz function x

—>

•

x is a minimizer.

References

[C] M. Chipot : Numerical analysis of oscillations in nonconvex problems. Numerische

Mathematik, 59, (1991), p. 747-767.

[C.C.] M. Chipot and C. Collins : Numerical approximation in variational problems with

potential wells. SIAM J. of Numerical Analysis, 29, 4, (1993), p. 473-487.

[D.] B. Dacorogna : Direct Methods in the calculus of variations, Springer-Verlag, Berlin,

(1989).

[F.] G. Friesecke : A necessary and sufficient condition for nonattainment and formation

of microstructure almost everywhere in scalar variational problems. Proc. Royal Soc.

Edinburgh 124 A (1994), p.

437-471.

[P.] P. Pedregal : Parametrized measures and variational principles, Birkhauser, 1997.

Boltzmann Equation for Quantum Particles

and Fokker Planck approximation

Miguel Escobedo

Departamento de Matematicas

Universidad del Pais Vasco

Apartado 644

Bilbao 48080. Spain

Abstract

We consider in these short notes a simple case of homogeneous Boltzmann equation for

quantum particles and its Fokker Planck approximation. Namely the Boltzmann Compton

and Kompaneets equations. We solve the Cauchy problem associated to these two equations

and prove global well posedness for a large set of initial data. We describe the long time

behaviour of the solutions and prove in particular that the solutions of the Boltzmann

Compton equation with suficiently large initial data undergo Bose condensation in infinite

time.

We finally show that for some initial data, the Kompaneets equation is a good global

approximation of the Boltzmann equation for all time t > 0.

Boltzmann equations for quantum particles

Consider a homogeneous dilute gas of two species of interacting quantum particles.

Let f(p, t) and F(p, t) be the densities of particles of each species that at time t have a

momentum pel

. Following [UU], [GLW] and others, the evolution of / and F may

be described, under the hypothesis of molecular chaos, by the following system:

= Q

ltl

(F,F) + Q

(F,f) F(0,.) = F

The collision terms Qi

i(F,F) and Q2,2(f,f) stand for collisions between particles of

the same species and are given by

iii

(*,*)= fff W

[*'*',(l

T*)(l

T*,)-***(l

'-*')(l + '-*'.)]dp.dp'dp'.-

J J Js?

The collision terms Qi,2(F,f) and Q2,i(f,F) stand for collisions between particles of

the two different species, they are given by

Qi,

(F,/)= fff W

,a(F

f',(l+rF)(l+

f,)-Ff,(l+TF')(l+Kfl))dp,di/di/„

with a similar expression for Q2,i(f,F). In both cases, Wij(p,p

,p',p'

) are given

measures and r and re may take the values —1,0 or 1 depending on the quantum

properties of the particles. If F (respectively /) is the density function of particles

which obey the Fermi statistics (in short which are fermions), then r = — 1 (respectively

= —

1).

If on the other hand F (respectively /) is the density function of particles

which obey the Bose statistics (in short which are bosons), then r = 1 (respectively

= 1). Finally, if F (respectively /) is the density function of non quantum particles

then T = 0 (respectively re = 0).

We consider in these notes the interesting example of the Boltzmann-Compton equation

which describes the photon- electron scattering. We denote by F the density function

of the electrons (which are fermions) and / that of the photons (which are bosons).

This makes that r = — 1 and re = 1. We assume that the electrons and photons have

low energy and low density from where, after some physical considerations we may

(i) suppose that the electrons are at non relativistic and classical equilibrium F(p) =

(ii) neglect the photon-photon interaction and Bremstrahlung effects.

Since the electrons are assumed to be at equilibrium, the first equation in the corre-

sponding system (S) drops. Moreover, by (i), the main contribution in the right hand

side of the second equation of (S) comes from the Q2,i term, corresponding to photon-

electron interactions. Then, the system reduces to the following equation for the photon

density:

%(jp,t) = f S{p,p',m)[e-Mf(p',t)(l + f(p,t))-e-^y(p,t)a + f(p',t))}dp',

where m is the mass of the electron (the photons have no mass), and S(p,p',m) is

a function explicitly known (cf. for instance [EMV2]) which depends on the type

of the interaction photon- electron. If we assume, for the sake of simplicity, that

f(p,t) = f(\p\,t) = f(k,t) with k = \p\, after some straightforward calculations, using

in particular specific properties of the function S, one obtains the Boltzmann-Compton

equation

(1) k

^ = j^°{f

+ f)e~

- f(l + f')e-

')k

b(k,k',m)dk'

(f,f)

A similar homogeneous Boltzmann equation arises if we consider bosons-fermions in-

teraction, with fermions at equilibrium. This is also a short range interaction and is

considered in [LY1] and [LY2] by numerical computations.

The system describing the interaction of non quantum particles, corresponds to the case

r = K = 0. Moreover let us consider for our purpose, an homogeneous gas composed

of heavy particles, with density function F, and light particles with density function /,

under the physical assumptions:

(iii) low concentration of heavy particles: so that we may neglect the collisions of heavy-

heavy particles.

(iv) in the heavy-light collisions, the momentum of the heavy particle undergoes a

relatively small change.

We may then suppose that the heavy particles are at equilibrium, so that the first

equation drops, and the main contribution in the right hand side of the second equa-

tion comes from the Q2,i term, corresponding to heavy-lights particles interactions.

Therefore, the density of light particles satisfies the classical homogeneous Boltzmann

equation

(2)

%(p,t) = J

{w(p + q,q)f(p',t)-w{p,q)f{p,t)}dq.

where

w(j>,

q) is a given function, which depends on the equilibrium state of the light

particles and the kind of interaction heavy-light particles.

The behaviour of the solutions to these homogeneous Boltzmann equations may be very

different for quantum and non quantum particles. In particular, in the case of quantum

particles Bose-Einstein condensation is possible asymptotically in time as it is proved

in [EM2] and we briefly explain below (see Section 5).

Fokker Planck approximation

It is well known that Boltzmann equations for gases of classical particles may be approx-

imated by Fokker Planck equations (cf. [LP] §21). The interest of this approximation

is that, as we shall see below, the resulting equation is a partial differential equation

which is simpler than the original Boltzmann equation. But on the other hand this

approximation may happen to be only valid for p in a subdomain of R

Consider for example the classical Boltzmann equation (2). By the condition (iv) above,

the measure w(p,q) decreases rapidly as q increases. Therefore, the main contribution

in the integral term comes from the region where q is small. The idea is then to perform

the following formal Taylor's expansion:

w(p + q,q)f(p + q, t) ~ w(p, q)f(p, t) + q

•

(w(p,

q)f(p, t))

+ 5

5>*&

{W(P

9)/(P

))

from where we obtain the following Fokker Planck equation:

with

Ai = / qiw(p,q)dq,

itj

= - qiqjw(p,q)dq

This,

and more general situations for classical particles, have been extensively stud-

ied in the physical and mathematical litterature. Among the recent works where this

question is considered from a mathematical point of vue, we may quote in particular:

[D],

[DL], [AB] and [VI]. The general mathematical framework of these studies is to

consider a family of "regular" cross sections w

which concentrate as e

—>

0 to the region

where q = 0 and show that, under suitable conditions on w and w

, the solutions f

(P>

) = / {weip + q,q)fE{p + q,t)-w

(p,q)f

{j>,t)}dq,

converge to the solution of the Fokker Planck equation, as e

—•

We understand very well at this stage that, for classical particles, as soon as one of the

two species is at equilibrium, the remaining Boltzmann equation is linear, and so is the

approximating Fokker Planck equation.

If on the other hand, the particles which are not at equilibrium are supposed to have a

quantum nature, the equation remains nonlinear, and so is the resulting Fokker Planck

approximation. Let us show this with the Boltzmann Compton equation.

Fokker Planck approximation of (1): the Kompaneets equa-

tion

The Fokker Planck approximation of (1) which is known as Kompaneets equation [K]

reads:

(3)

-l^K +

/»-

>^>°-

The formal deduction of this equation from the original Boltzmann Compton equation

is as follows. One first considers that the main contribution in the collision integral

/>oo

/ {f'(l + f)e-

-f(l + f')e-

')k

k'H(k,k',m)dk',

comes from the region \k'

—

k\ « k so that:

/(*') ~ f(k) + (fc' - k)f{k) + i(*' - k)

f"(k)

' ~

- (k' - k)e~

+ -(fc' - fc)

from where

with

( r°°

/ (/' (1 + /) e"

- /

+ /') e~

') k

b(k,

k')dk'

. ~ A(k)f(k) + (A(k) + B(k))f'(k) + B(k)f"(k) + 2B(k)ff +

A(k)f.

r°° i

A(k) = / ((fc' -k)-Uk' - k)

)b{k, k', m)e-

dk'

Jo 2

B(k) =

/ (it' - k)

b(k, k', m)e~

dk'.

2 Jo

a(fc) = exp / -gf-^rda

{a)

(*) = B(fc)exp(-/' ^4da)

JO #((7)

So that, if we define

and

we have

*^~

7(fc

)^[a(

)(|+ / +

/')].

On the other hand, the law of conservation of the total number of particles in the process

of scattering requires that the equation should have the form:

-V-

where J is the photon flux in momentum space. Because of the isotropy of the photon

distribution function, the divergence of the flux has the form:

Therefore we get that j(k) is a constant.

Finally, using the explicitly known function b(k, k', m) (cf. for instance [EMV]) it is

easy to show that as k/m ->0we have, B(k) ~ fe

. This gives

dt dk

l x

for some positive constant C.

2df

-ci-[k\

J-

+ f +

f% as i-0.

It is important to notice that in the classical Boltzmann equation under condition (iv),

the collisions for which p

—

p' is small are much more important than collisions with

large momentum changes. On the other hand, since Compton scattering is a short range