Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

450

[8] A. Osses, J. P. Puel, Approximate controllability for a linear model of fluid structure

interaction,

ESAIM:

Contr. Optim. Calc. Var., 4 (1999) 497-513

[9] A. Osses, A rotated multiplier applied to the controllability of waves, elasticity and

tangential Stokes control, to appear in SIAM J. Control Optim.

[10] O. Pironneau, Conditions aux limites sur la pression pour les equations de Stokes et

Navier-Stokes, C.R.

Acad.

Sc. Paris, 303 (1986), Serie I, No. 9, 403-406

[11] R. Verfurth, Finite element approximation of incompressible Navier-Stokes equations

with slip boundary condition, Numer. Math., 50 (1987) 697-721

[12] R. Verfurth, Finite element approximation of incompressible Navier-Stokes equations

with slip boundary condition II, Numer. Math., 59 (1991) 615-636

Hyperbolic propagation of singularities in a parabolic

system of shell theory

J. Sanchez-Hubert

Mathematiques et Mecanique, Universite de Caen

Boulevard Marechal Juin, 14302 Caen, FRANCE

E-mail : jsanchez@mecaunicaen.fr

Abstract

The mechanical properties of shells are concerned with the membrane system.

When including the smoothing terms of flexion, which are small for thin shells, the

singularities become narrow layers, it is easily seen that the energy concentrates

in these layers. For parabolic surfaces, by choosing appropriate parameters, we

may solve the system step by step. Each step equation of order 1 is hyperbolic

with simple characteristics coinciding with the generators. Classical hyperbolic

propagation of singularities applies. We give the corresponding transport equation

of the singularities. At each step the effective data involve the components of the

loading and some derivatives of the unknowns considered in the previous steps, so

that this process implies singularities of increasing orders.

1 Introduction

We present a class of systems of PDE (issued from shell theory) which are parabolic.

Their structure is such that they may be solved by a sequence of step equations. Each

step equation is hyperbolic, so that classical propagation of singularities theory applies.

Moreover, at each step, the effective data involve some derivatives of the unknowns con-

sidered in the previous steps, so that this process implies singularities of increasing orders

along the chain. For instance, a singularity of the data f

along the characteristic y

= 0

of the form

where Y is the Heaviside function and F

denotes a smooth function, implies a singularity

of the unknown u

of the form

~ 6'" (y

) U

) ,

where C/3 (y

) satisfies genuine transport equation so that it may be different from zero in

regions where F

= 0.

451

452

Such a situation is in evident contrast with the behavior of the "model parabolic heat

equation" :

du d

u _

where the presence of the time derivative classically implies hypoellipticity (see for in-

stance [8], page 145) i.e. u is of class C°° in an open set whenever / is also C°°, so that

singularities cannot propagate.

The mechanical behavior of a shell (in the Kirchhoff Love model) in the static case is

described by two energy forms (see for instance [1] and [6]) :

(u, v) : membrane bilinear form

a,f (u, v) : flexion bilinear form.

Let A

and E

Af be the operators associated with the two bilinear forms a

(u, v)

and e

a,f (u, v) respectively. Then A; is elliptic and Am is of the same type as the points

of 5. Its characteristics are the asymptotic curves of S. For e > 0, the energy space V is

such that

+ e

a,f is continuous and coercive on V.

In the sequel, we only consider the case when the surface S, along with the kinematic

boundary conditions, is geometrically rigid in the linear sense. This amounts to the prop-

erty that a

(v,v) = 0 => v = 0. As the order of differentiation in Af is higher than

in A

, a singular perturbation phenomenon appears when e \ 0. Moreover, as the limit

process e \ 0 goes from a higher order elliptic problem to a lower order parabolic (or

hyperbolic) one, the limit process e \ 0 is non-standard.

For E \ 0, the limit problem involves a new energy space V

for which the bilinear

form a

is continuous and coercive :

is the completion of V for the norm y/a

(.,.) (which is norm as a consequence

of the above mentionned geometric rigidity).

contains functions less smooth than those of V.

Consequently, the solutions u

belong to V, but their limit as e \ 0 is a less smooth

Junction : u

exhibit boundary layers for small e.

We have the embeddings

VcV

VicV,

so that the usual loadings / 6 V are admissible for the variational problem for e > 0, but

it may happen and often happens that f £ V

It will proved useful to consider the system of PDE occuring in the membrane shell

theory (i.e. the limit problem for e = 0) :

f -Dpi** = f

\ -b

T°e = f

(1)

453

where

rpa(3 AafBXy.

(Dxu^ + D^ux -

Xli

)

(2)

are the stress components and u the displacement vector. The variables are y

and y

which describe the middle surface 5 of the shell, D

denotes the covaxiant differentiation

on the surface (Throughout this work, the notations are those of surface theory, see for

example [6]). The above coefficients b

p are smooth given functions. They are indeed the

coefficients of the second fundamental form of the surface S. The coefficients

a0X,x

are

also smooth given functions, namely the membrane elasticity coefficients. They satisfy the

classical symmetry and positivity hypotheses. The unknowns are the stresses T

a/3

and the displacement components

(the greek and latin indices run in {1,2} and {1,2,3}

respectively); u

are the covariant tangential components and

is the normal component

to the surface. The given loading / is defined by its contravariant components /* with f

normal to the surface. The system (l)-(2) contains six equations and six unknowns Uj,

, T

and T

; its total order is four.

In the sequel, we shall consider the case of an everywhere parabolic middle surface,

that is the second fundamental form is degenerated. It is easily checked that system (1)-

(2) will then be parabolic in the following sense. Denoting

(£) the principal symbol

of the system, det

[Do

(£)] = 0 has one root £ of multiplicity 4. More precisely, the

corresponding characteristic (with multiplicity 4) coincides with the asymptotic direction

of the corresponding points of 5 (which is double in the parabolic case).

It is well known in surface theory that the set of surfaces everywhere parabolic coincides

with the set of developable surfaces. Then, choosing the parameters y

and y

, with y

along the generators, we have

= b

= 0, b

^ 0. (3)

Moreover, taking the curve y

= 0 orthogonal to the generators, the Christoffel symbols

are such that

iTx = r£ = 0. (4)

We have the following criterion in order to determine if a given loading belongs to V^

or not :

Theorem 1.1 A necessary and sufficient condition for f to belong to V^ is that there

exists T

P G l? (S) satisfying (1) and the boundary conditions T

^n^ = 0, on the free

parts of the boundary. Here

is the unit normal to the boundary in the tangent plane.

This theorem and its proof are analogous to those of Section 2.2 in [4].

Using this criterion, let us give an example of loading / with a jump (then not so

much singular!) such that / does not belong to V^ :

454

Theorem 1.2 Let us consider a shell the middle surface of which is developable and such

that b

7^ 0. Let the loading f defined as /1 = /2 = 0, and with U

=/=

0 a piecewise

smooth with a jump discontinuity along a part of a generator. Then f does not belong to

V .

Proof.

The limit problem in terms of the stress components write

where l\™ = 0, since the sin-face is developable. The last equation immediately gives

n22 _ h

b22(y

Then, if we assume, to fix ideas, /

, y

) = F (y

) Y (y

), where Y (y

) is the Heav-

iside function, we get

= — -

F(y

)Y(y

)

b22(y\y

)

and (5) becomes

f -DjT

= 0

T- -

= ^6

)

+ (T£ + 21-) Wim ^

\ °22 022

The second equation is a differential equation with respect to y

with parameter y

the solution of which is classically

T" = 6(y

)<S>(y\y

)+y(y\y

)+K(y

where

and

*(2/V):= f exp-

/V^,!/

Jo Jo

F(n)

* (y\ y

) := Y (y

) J^ exp (- J^ 3I\

(£, y

) df) (i^ + 2r

) ^dn.

Clearly, * € L

((0, J^ x {-l

)), * € L

((0, Ji), tf"

(-I

, J

)) and A

€ H~

(-l

, l

As the function $ depends on y

and K is only a function of y

, the solution T

cannot

belong to L

(fi) and according to 1.1 the conclusion follows. •

We are mainly concerned with the propagation of the singularities of system (l)-(2).

We consider the classical sequence of distributions on R with increasing singularities

•••,xY(x),Y(x),S(x),6'(x), ••• (7)

455

where Y and S denote the Heaviside function and the Dirac mass respectively. More

precisely, these distributions are considered as singularities at x = 0 whereas their values

for x ^ 0 are discarded. For instance Y (x) is considered merely as the unit jump at x = 0.

For instance, in order to describe the singularity of T

along y

= 0, we consider

expansions of the form (for example)

T"~#(v

(

) + 6(v

)B"(y

) + ... (8)

where it is understood that the terms

• • •

are less singular than the previous ones at y

= 0.

Such kind of expansion is in the framework of discontinuous solutions (see for instance

works by Egorov & Shubin [2], Sanchez Palencia [5] and Gerard [3]).

We always assume that the geometric data and the coefficients are smooth, so that

the sequence (7) is consistent with the singularities of the solutions, provided that the

singularities of the data are in that sequence, which covers most of the usual examples.

2 Singularity along a characteristic due to a discon-

tinuity of the loading /

Let us assume that the parameters belong to the domain O = (0,1) x (0,1) and that the

boundary conditions are such that the shell is inhibited, for instance fixed along y

— 0

and free elsewhere :

u(0,y

)=0. (9)

Denoting by n the unit normal to the boundary in the tangent plane we have on the

free part Ti = {y

= 1} of the boundary the natural boundary conditions

afi

= 0

which give

f ^(l.V

) = 0,

(l,y

) = 0.

(10)

Indeed, n//a

which implies that n\ ^ 0 and «2 = 0. As an example, let us consider

the loading

r = o,

f = Y(y

-c

lalM]

(yi)F(y\y

where Y is the Heaviside function, 0[

i,f,i] is the characteristic function of an interval

[a'jfc

] C [0,1] and F denotes a smooth function. The jump of /

lies along the internal

characteristic y

= c

and according to 1.2 / does not belong to V

. Obviously a boundary

layer appears along y

= c

Equation (6)2 is hyperbolic of order one for T

. The main singularity (in the sense of

(7)) in the right hand side is 6 (y

—

) #[

i,j,i] {y

)

Fty

Consequently, we search T

^6(y

-c

(y')+---

Then, A

satisfies the transport equation

^ + 2r

= V,M](2/

)*(2/

), (11)

456

where

)

F^c

). The boundary condition T

(l,y

)

= 0

gives A

(1)

= 0.

Consequently, the equation (11) completely determines the unknown A

. More precisely,

we have

)

S(„)exp|T 2r

(£)d£

xexp (-2j

(Odt

drj

Cexpl 2rf

(0de

for 0

< y

for a

< y

< ft

for b

< 1,

where

the

constant

C is

such that

)

continuous

at y

= 6

We observe that

)

= 0, for 0 < y

< a

, but in

general

)

^ 0 for b

< y

< 1,

though

i (,i|

= 0 :

this

the phenomenon

propagation of the singularities.

the solution

the equation (similar

(6)i)

022

the main singularity

which

the right hand side

is in

8' (y

—

Consequently,

search the main singularity

T»c6'(y

-c

)A»(y

(12)

where

appears that

)

solution

the equation

dA"

dyi

the solution

which is determined

before using the boundary condition

(1)

= 0.

Now, we consider the system

(2)

+ r

yp/3A/i

D^ux -

)

At the leading order

singularities

the sense

(7) this gives

lUl

SuuT

2211

(ftui

9i«

)

1211

(13)

where Sapx^ are the comphance coefficients (5 is the inverse matrix of A). Then we search

the main singularity

the components

(

S'(y

-c

8"(y

-c

(14)

8"'{y

-^)U

457

Substituting (14) into (13), we immediately obtain, taking into account the boundary

condition at y

= 0

)

= [

(Z,c

(Od£.

Then U

is obtained from (13)3

which gives, with the boundary condition U

(0) = 0

)

= - jT U

fo)

exp

(- jf

2T\

(0 d£

)

drj.

Jo \ Jo /

At last, we obtain

yl) =

(yWY

3 Numerical simulations

In this section, we present numerical simulations for the system

(u, v) +

(u, v) = (f, v),

(see section 1) with e = 10~

. Numerical simulations allow us to exhibit the phenomenon of

propagation of singularities, more precisely, thin layers which converge to the singularities

for e \ 0 see [7].

The developable surface S is the cone parametrized by

^ / SI -> S

\{y\y

) ^ (y

,(y

-a) sin (2Try

),(y

-a) cos (2Try

)), a> 1

where ft = (0,1) x (0, |), the image of the mapping being presented in the following

figure :

The numerical computations are implemented with Hermite finite elements. The exact

numerical integration of the rigidity matrices needs six Gauss points. In this case, the

error estimate is of order O (ft

The meshes for the domain H are generated using the Modulef code. The mesh is

obtained in order to perform the refinement of the mesh in the vicinity of the layers (see

hereafter) using a distribution function of the points, according to a geometric progression

with ratio q.

458

Figure 1: Mapping of the cone : fi = (0,1) x (0,0,5) ; x = y

, y = (y

+ 2) sm2ny

z = {y

+ 2) cos 2ny

3.1 Characteristic internal layers and propagation of the singu-

larities

Let us consider the loading

where

= (0,0,-y(

-l)K(y

-i))

' 1 0 if y

< 0.

The numerical results are shown on figure 2

We observe an internal layer along the whole characteristic y

= 1/4, while the dis-

continuity of the data is only along the interval 1/2 < y

< 1.

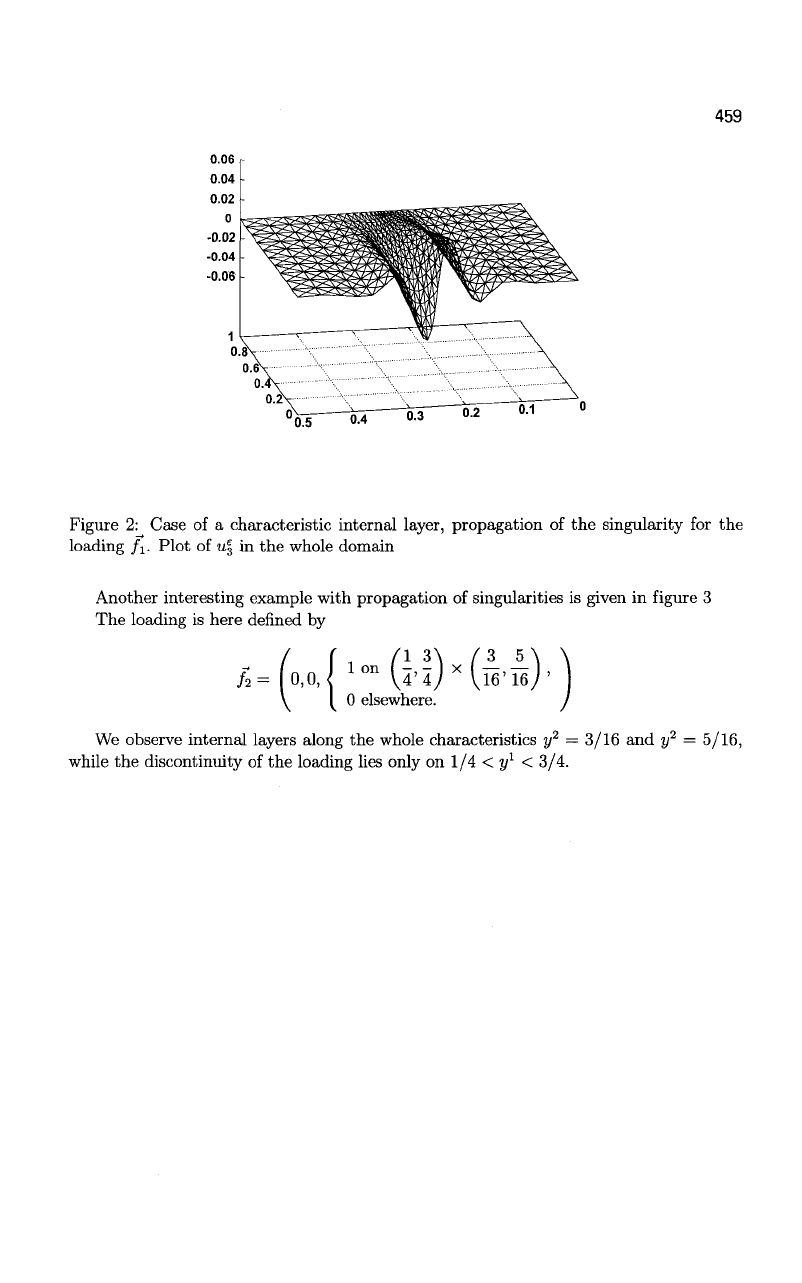
459

Figure 2: Case of a characteristic internal layer, propagation of the singularity for the

loading /j. Plot of u| in the whole domain

Another interesting example with propagation of singularities is given in figure 3

The loading is here defined by

£=(o,

ion

(i'£)

V I 0 elsewhere.

>•)

We observe internal layers along the whole characteristics y

= 3/16 and y

= 5/16,

while the discontinuity of the loading lies only on 1/4 < y

< 3/4.