Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

430

4 Qualitative properties of the solution

4.1 Nonnegativity of the solution

Proposition 4.1 For almost every [r,z,t) m]0,l[x]0, l[x]0,T[, and fori €

{1,...

,N},

one has : 0 < C;/ (r, z,t), 0 < C

(z,

t).

Proof.

This is proved multiplying the equations of (1) by the non-negative parts of df

or C

, respectively. •

4.2 Upper and lower bounds of the concentrations

Proposition 4.2 1. Let Si =

—1.

For almost every (r,z,t) in ]0, l[x ]0, l[x ]0,T[, we

have : 0 < C

(r, z,t) < A

; 0 < C

(z,t) < Am, with:

= max sup C

(r), sup

is0

(z)

Yre[o,il *e[0,i]

Let Si = 1. For almost every {r,z,t) in ]0,1[ x ]0,1[ x ]0,T[, we have: a

(r, z,t) , a

< C

(z,t),

with :

= min I inf C

(r), inf

is0

(z)

\7-e[o,i]

e[o,i]

Let 6i = l. For almost every (r, z, t) in ]0,1] x ]0,1[ x

]0,

T[ one has : df (r, z, t) <

, C

(z, t) < a

, with :

= max sup C

(r), sup

is0

(z)

I ;

= sup k

Yrslo.i] zs[o,i]

ki being the Lipschitz constant of the function r^.

4- Let Si = 1. There exist two positive constants a and b such that for every I in ]0,1[

and for every T > 0 :

i I {C

)

{r,l,t)r{l-r

)drdt < aT + b,

J o J o

/ (ds)

(z,T)dz < aT + b.

J o

Proof.

The verification of these qualitative properties of the solution is essentially

obtained multiplying the equations of (1) by the appropriate non-negative or non-positive

parts of the corresponding test-functions. •

431

5 Numerical simulation for the reaction CO + 0

—>

In the fluid, we use the following discretization method :

• If i is different of N (chemical species), we directly solve (l)i using the method of

finite differences or that based on finite elements. This requires that the equation

with i = N has already been solved in order to put the appropriate values of

UN-

• If i is equal to N (temperature) we evaluate the coefficients at the step before. This

possibly requires the use of some fixed point argument.

On the boundary, we still use some finite differences method or some finite element

method (see [2] for the details).

Let us take the following initial and boundary conditions:

within the cylinder

CO{r,Q,t) = 0.02

(r,0,t) = 0.05

(r,0,i) = 0

T(r,0,t) = 500,

on the boundary CO (z, 0)

(z,0)

T(z,0)

= 0.02

= 0.05

= 0

= 490,

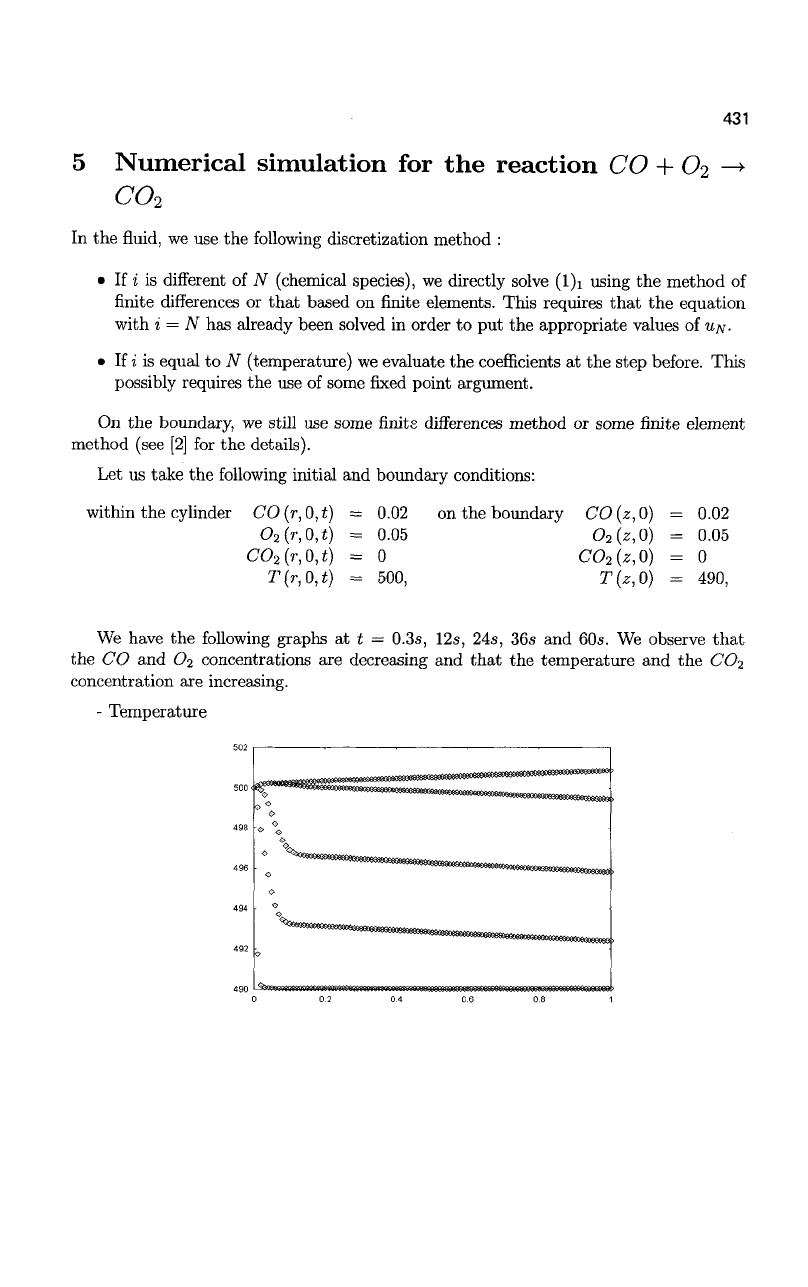
We have the following graphs at t = 0.3s, 12s, 24s, 36s and 60s. We observe that

the CO and O2 concentrations are decreasing and that the temperature and the CO2

concentration are increasing.

- Temperature

490

'^TOWMOMasMMqMffWireflagtBtwowgi 39TOt»?C0000C30OtO0eCMflC00Cfi0«»8C

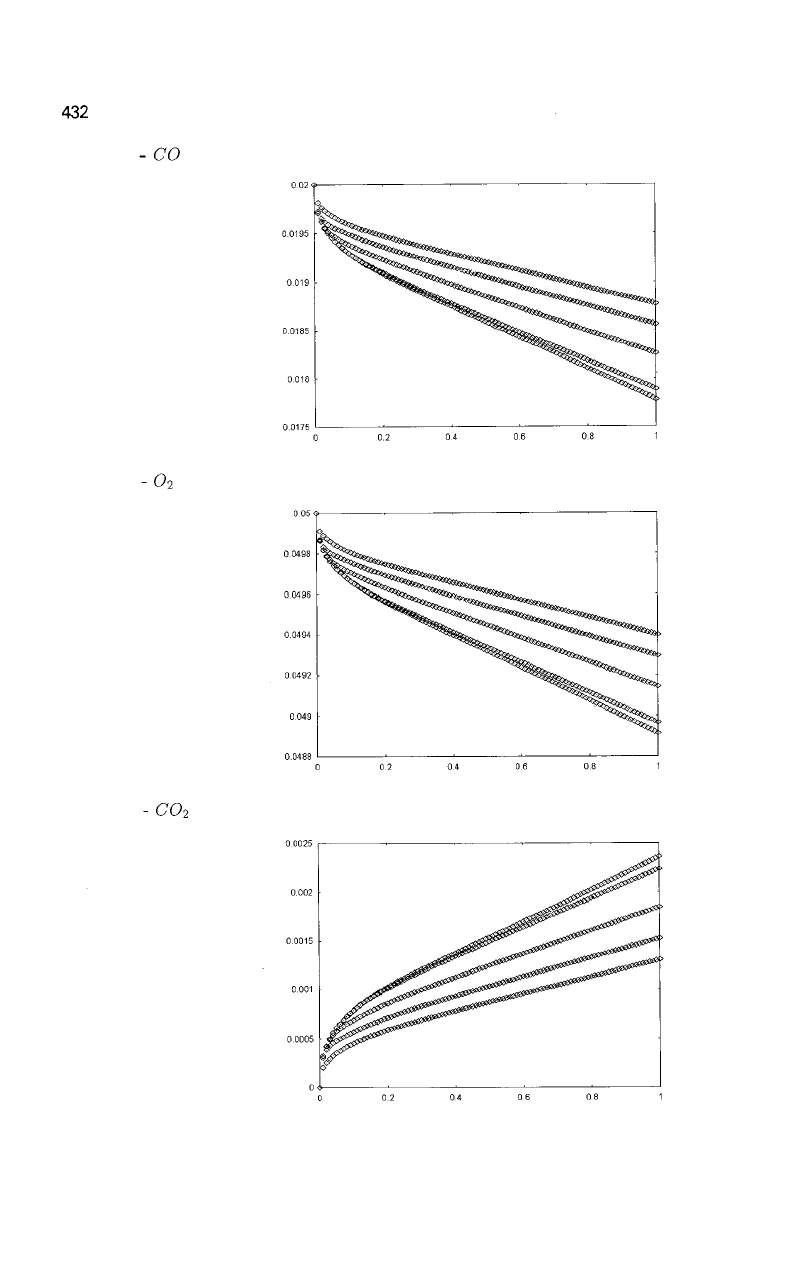
432

433

Remark 5.1 The reaction ends after 54s with the following values at the outlet of the

cylinder (z = 1):

(70(1,54) = 0.017777,

(1,54) = 0.048912,

(1,54) = 0.002355,

T(l,54) = 500.873497.

References

[1] J.-D. Hoernel, Etudes theorique et numerique d'un modele non-stationnaire de catal-

yseurs a geometrie cylindrique. PhD thesis, Universite de Haute-Alsace (2002).

[2] J.-D. Hoernel, Aspects numeriques de l'etude d'un modele non-stationnaire de catal-

yseurs a passages cylindriques. Actes de la journee CRESPIM du 24 Janvier 2002,

Universite de Haute-Alsace (2002).

[3] A. Kufner, Weighted Sobolev spaces. Teubner-Texte zur Mathematik, 31. BSB B. G.

Teubner Verlagsgesellschaft, Leipzig (1980).

[4] J. Malek, J. NeCas, M. Rokyta and M. RuziCka, Weak and measure-valued solutions to

evolutionary PDEs. Applied Mathematics and Mathematical Computation 13, Chap-

man & Hall, London (1996).

[5j M.J. Ryan, E.R. Becke, K. Zygourakis, Light-off performance of catalytic converters.

The effect of heat/mass transfer characteristics. SAE 910610 (1991).

[6] E. Zeidler, Nonlinear functional analysis and its applications. Springer-Verlag, New-

York (1985).

Exact controllability of piezoelectric shells

Bernadette Miara

Laboratoire de Modelisation et Simulation Numerique

Ecole Superieure d'Ingenieurs en Electrotechnique et Electronique

2 boulevard Blaise Pascal, 93160 Noisy-le-Grand, Prance

Email : miarab@esiee.fr

Abstract

We propose a dynamical model for piezoelectric thin shells and we establish,

using the multiplier technique, an observability result. Then, by applying Lions'

Hilbert Uniqueness Method, we prove that exact controllability can be achieved

with a control vector field acting on the whole boundary of the shell.

1 Introduction

Latin indices and exponents take their values in the set

{1,2,3},

Greek ones take their

values in the set

{1,2}.

Einstein's summation rule is used. Boldface symbols represent

vectors or vector spaces.

We examine first the linearized piezoelectric effect in a three-dimensional body. Let

T > 0 and n be a domain in R

with C

-boundary T. We denote by Q the domain

Q = fi x (0,T) and by E its boundary: E = T x (0,T). The equations modelling the

time-evolution of the elastic displacement field y = (jk) : Q —• R

, and of the scalar

electric potential 9

—>

R of a piezoelectric body without any volumic electric charges

or mechanical forces are given by:

f y" + A(y,0) = OinQ,

\ B(y,8) = OinQ,

with the boundary control and the initial conditions

y = w on E,

6 = w on E,

y(0) = y° in 0,

y'(0) = y

infi,

with

<9v —

y" =

y"(x,t)

-g^(x,t),

y(0) = y(x,0), y'(0) = -£{x,0), x 6 fi, 0 < t < T.

434

435

These equations are of the divergence type: A = —divT and B = — div<5 where the

second Cauchy stress tensor T and the electric displacement S are related through the

constitutive equations

TV(y,0) = c^

{y) + e^d

fi*(y,0) = -tPsuW + dVdjO,

where (s

i) is the linearized deformation tensor s

(y) = (d

yi + diy

)/2. The material is

characterized by three time-independent tensors: the symmetric positive-definite tensor of

three-dimensional elasticity

ufc

'),

the symmetric coupling tensor (e

*) and the symmetric

positive-definite dielectric tensor (d

«H

= c

ku^

3ac>0

Xij

ij:

\/X

= X

G R,

= e

ikj^

= d

ji^

3ctd>0

. tfiXiXj > a

XiXi, MXi € K.

We have shown in [6] that, for a star-shaped domain fi with respect to x° 6 R

it is possible to build a control (w,w) 6 L

(S) x L

(E) acting on the whole boundary

E such that system (1) can be driven to rest after time T° = 2max

jj |x

—

x°|, i.e.

y(t) = y'(t) = 0,t> T°.

The aim of this paper is to extend this approach to thin piezoelectric shells. In

section 2 we propose a new time-dependent model for Koiter-type piezoelectric shells.

In section 3 we study the properties of the homogeneous evolution problem and derive

direct and indirect inequalities obtained by the multiplier technique. This leads to an

observability condition which allows, in section 4, to establish the exact controllability

conditions. Finally, in section 5, we sum up all the results already obtained for three- and

two-dimensional structures.

2 A time-dependent model for Koiter-type piezoelec-

tric shells

In order to avoid introducing new notations, we will use the same ones for the two-

dimensional problem as for the three-dimensional problem. Thus, let

be a domain in

with boundary T of class C

and x = (xi, x

) € fi a system of curvilinear coordinates.

The middle surface 5 of the shell is given through an injective mapping ip e C

(f2;R

S =

<p{fl).

We assume that the vectors (a„ = d

ip) are linearly independent, so that they

define the tangent plane at each point of S. The reference configuration of the shell with

thickness 2e is the closure of the set

{<p(x) +

(x),

xeQ, \x

\ < e}.

where a

is the unit normal at each point of S.

|ai x a

436

2.1 The static problem

By an asymptotic analysis, Ch. Haenel has shown in [3] that the limiting two-dimensional

model of a piezoelectric shell depends on the geometry of the middle surface S. He

established that (as in the pure elastic case) the solution of the three-dimensional problem

converges, as the thickness of the shell goes to zero, to the solution of either a "membrane-

dominated" model with a piezoelectric coupling effect or a "flexural-dominated" model,

where the elastic and the electric effects are decoupled.

Following Koiter's approach for elastic shells, we propose the following static equa-

tions with mechanical clamping conditions on the lateral boundary and no electric sur-

face charges. The unknowns are the three covariant components (j/;) : O —> R

the elastic displacement field and the scalar electric potential 6 : fi —• K

. They

are,

for all applied volume forces f e L

(£2), the unique saddle-point in the space

[[^(Q) x ffi(n) x

Hg(Q.)]

x H^(Q)] of the functional

(v,V<)

- /

(v, v) + 2e (v,

ip) —

d(ip,

ip)]

i/adx

—

/ f

•

v^/adx

with

CM(y.v) = c^-

7a/3

(y)

(v),

<*(y,v) = <f*"

f,(y)p„{v),

c(y,v) = c

(y,v) + yCi?(y,v),

e(v,^) = e<"%

(v)cW,,

where (7

Q/3

) is the two-dimensional linearized change of metric tensor, (p

a/3

) the two-

dimensional linearized change of curvature tensor and where c

a/3

°"

, e

a/3r

and d

a/3

are two-

dimensional tensors with the same properties of symmetry and positivity of the analogous

three-dimensional tensors. (For a description of these tensors in the case of a Saint Venant-

Kirchhoff material, see Haenel [3]).

2.2 The time-dependent problem

Associated with the static problem, we can introduce the time-dependent problem. Let

T > 0 and, as for the three-dimensional problem, we note Q = fi x

(0,

T), E = T x (0, T).

The time-dependent covariant components of the displacement field and of the scalar

electric potential solve the following system of P.D.E.

(2)

f y" + A(y,0)

B(y,0)

dnVi

y(o)

y'(o)

y°

inQ,

on E,

in fi,

in SI,

437

where d

stands for the normal derivative.

The control problem, (see the differences in the boundary conditions between the three-

and the two-dimensional problems) we are interested in, is therefore: Is it possible to find

suitable initial conditions (y^y

), boundary control (w,w),u;) (i.e. in which functional

spaces does it belong) and minimal control time T° so that the system can be driven to

rest after T° ? As a first step to the study of this problem, we establish useful properties

of the related homogeneous problem.

3 The homogeneous problem

We consider the homogeneous problem

u" + A(u,4>) = 0 inQ,

B(u,<£) = 0 inQ,

u = 0 on E,

= 0 on E, (3)

= 0 onE,

u(0) = u° inO,

u'(0) = u

inQ,

We denote by V

= #

(Q) x H

(Q) x tf

(0) and V

= if*(ft) x Hl{U) x Hg(Q) the

functional spaces associated with the strong and the weak solutions of (3).

Theorem 3.1 Let fi be a domain in M

with boundary T £ C

and T > 0

(i) For (u°, u

) e V

n V

x V

system (3) has a unique strong solution

(u, u') e C(0, T; V

n V

x V

e C(0, T; H

(Q) n

H^(Q)).

(ii) For (ii^u

) e V x L

(fi), system (2) has a unique weak solution

(u,u') eC(0,T;V

(I!)),

<j>

e C(0,T;H*(Q)).

(Hi)

The

energy

E(t) = |

(|u'|

c(u,

u) +

d(<j>,

<j)))^/adx, associated with

weak solu-

tion,

constant over

all the

trajectories

E{t)

= E° = \ f

[|u

+ c

(u°,u°)

d{<j>°,<j>

)}

,/a~dx,

t > T,

f d{4>°,i>)^fa~dx

= /

e(u°,i/j)^dx, VV>

H^(n).

(iv)

The

weak solution satisfies Maupertuis' principle:

[|u'|

c(u,

u) -

d(<f>,

<(>)]^/a~dxdt

= /

[u'(T)

•

u(T)

—

•

u°]\fadx.

Jo Ja

where

438

(v)

The

weak solution satisfies

the

direct inequality also called "hidden regularity" prop-

erty:

for all

multipliers

q 6 C

(H)

[c(u,

u) +

2e(u,

<j>)

d{4>,

4>)]q •

n-^/arfE

<C(T+1)E°.

(vi)

For all x° £ K

there exists

constant

a = a(ip, Q),

that depends

on the

geometry

such that

the

weak solution satisfies

the

indirect inequality established with

the

multiplier

p = x

—

x°,

[c(u,

u) + 2e(u, 0) - dfa

4>)]p •

ny/ZdZ

> (1 -

<T)(T

T°)E°,

where

T° =

max

—

x°|.

Proof. The

proof

this theorem

obtained

for

steps

(i) and (ii) by

application

Hille-Yosida theorem.

For steps

(iii) and (iv) by

multiplying

the

equilibrium equations

by (u,

(/>),

(u',

<//)

and

by integrating

on n and Q.

For step

(v) we

make

use of the

multipliers technique. Indeed,

multiply

the

equi-

librium equations

gAii,

qidi(j>

and

integrate

on Q.

For step

(vi) we

the

same approach, with

the new

multiplier

q = p. •

Remark

3.2 1.

step

(v),

with

the

multiplier

q = n (the

unit normal vector)

on T, we get

[c(u,u)

2e(u,

<f>)

d(<f>,

4>)}y/E

(E).

Therefore

it is of

interest noting that

the

weak solution does

not

exhibit

the

classical

regularity condition obtained

for the

pure elastic shell

([5])

which

is c(u, u)^/a £

(E)

or, in

other words, <9

€

(E), <9

€

(E).

For a

computation

of a see

[5].

When

the

middle surface

S of the

shell reduces

to a

plane

the

quantity

vanishes.

The rest

this paper

devoted

to the

case

a < 1,

which

call

the

"shallow" shell

condition eventhough this differs from

the one

given

[2,

1].

For a < 1 and

T>T°

we get

-a){T-

T°)E°

< C J

[c(u,u)

d(<j>,

</>)]yfaIE.

Hence, when [c(u,u)

d(cj),

4>)]^fadT,

€

(f2),

we can

define

a new

norm

||(u°,

)!!

= y

[c(u,

u) +

d(0

0)]V^dS,

equivalent

to the

energy norm.

439

4 Exact controllability

The exact controllability is established thanks to Lions' Hilbert Uniqueness Method

(HUM). Associated with smooth initial conditions (u°, u

), we consider the adjoint back-

ward and the nonhomogeneous problem

with final conditions:

and boundary conditions:

v" + A(v,V;) = 0 iaQ,

B(v,V0 = 0 inQ,

v(T) = 0, v'(T) = 0 in fi,

v = d

u on E

V3 = 9nn«3 °n E

v = 0 on E \ E

= 0 onE\E

= —

<f>

on Ej

ip = 0 onE\Ei,

(4)

(5)

where E

= T

x (0,T), Ei = Ti x (0,T), T

and Ti being parts of the boundary dQ.

We introduce the operator A: (u^u

) 6 V(Q) x V{Q) -> A(u°,u

) = (v'(0),-v(0)).

Let (z,£) be the solution of the homogeneous problem with initial conditions (z^z

) e

V(Q) x D(fi). We formally have:

f A^u

)-^

)^ = f c(u,z)dE- /

e(z,<t>)dY,

JO. J So -'Si

+ ( e(u,C)d£+/ d(C,*)dS-

«/ So ^ Si

Therefore, when E

= E

= E, we can introduce, for (ii^u

) e V(Q) x £>(fi), the

semi-norm

IKu

)!!

/A(U°,U

)-(U°,U

)^=

/(c(u,u) + d(0,^))dE.

./n JE

Let us denote by F the Hilbert space which is the closure of V(Q) x

T>(SV)

for the norm

IKiAu

)!! and F' its dual, let

= (V

n V

) x V

, F

x L

C F C F

, (F^)' CF'C (F

))'.

Hence A is uniquely continued in an operator A : F —> F'. By transposition, for

, —y°) e F' and w £ L

(E), w e

(T,),

u e £

(E), there exists a unique weak

solution of (4) and we have the final result.