Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

150

Corollary

2.7.

Let K C

mxn

compact. Then

q>e

C(K)„,

)

K,,

particular,

c if,^

qfi

C^if),,,,).

Proof.

By the previous proposition C(K)

qfi

C(K)

qfix

and, clearly, .K^nC^-fiT),^

Remark

2.8. The

assertion that

qfiX

for

convex sets

implicitly contained

in [16,

Th. 1.5]. The

fact that

qfix

has

been pointed

out

[18].

Note that here

extended definition

2.5 to

nonquasiconvex sets.

Acknowledgment: Partial support

by the

grant

107

5005 (Grant Agency

of the

Academy

Sciences

the Czech Republic)

gratefully acknowledged.

References

[1]

ACERBI,

Fusco, Semicontinuity problems

in the

calculus

variations. Arch.

Rat. Mech. Anal.

(1986), 125-145.

[2]

E.M.

ALFSEN,

Compact convex sets

and

boundary integrals. Springer, Berlin, 1971.

[3]

J.M.

BALL,

version

the

fundamental theorem

for

Young measures.

In:

PDEs

and Continuum Models

Phase Transition. (M.Rascle, D.Serre, M.Slemrod,

eds.)

Lecture Notes

Physics 344, Springer, Berlin, (1989), pp. 207-215.

[4] K.

BHATTACHARYA,

N.B.

FIROOZYE,

R.D.

JAMES,

R.V.

KOHN,

Restriction on

microstructure. Proc.

Roy. Soc.

Edinburgh

124A

(1994), 843-878.

[5]

DOLZMANN,

KIRCHHEIM,

KRISTENSEN,

Conditions

for

equality

hulls

the

calculus

variations. Arch.

Rat.

Mech. Anal.

154

(2000), 93-100.

[6]

KINDERLEHRER,

PEDREGAL,

Characterizations

Young measures generated

by gradients. Arch.

Rat.

Mech. Anal.

115

(1991), 329-365.

[7]

KREIN,

MILMAN,

extreme points

regularly convex sets. Studia Math.

9 (1940), 133-138.

[8]

KRUZI'K,

Bauer's maximum principle

and

hulls

sets. Calc. Var.

and

PDEs

(2000),

321-332.

[9]

MATOUSEK,

PLECHAC,

functional separately convex hulls. Discrete Corn-

put. Geom.

(1998), 105-130.

[10]

C.B.

MORREY,

JR.,

Quasi-convexity

and the

lower semicontinuity

multiple inte-

grals.

Pacific

Math.

(1952),

25-53.

[11]

C.B.

MORREY,

JR.,

Multiple Integrals

in the

Calculus

Variations. Springer,

Berlin,

1966.

[12]

MULLER, Variational models

for

microstructure

and

phase transitions. Lecture

Notes

the Max-Planck-Institute No.

Leipzig, 1998.

[13]

PEDREGAL,

Laminates

and

microstructure. Europ.

Appl. Math.

(1993), 121-

149.

151

[14] R.T.

ROCKAFELLAR,

Convex Analysis. 2nd ed., Princeton, New Jersey, 1972.

[15] V. SvERAK, Rank-one convexity does not imply quasiconvexity. Proc. Roy. Soc.

Edinburgh 120 (1992), 185-189.

[16] K.

ZHANG,

On the structure of quasiconvex hulls. Ann Inst. H. Poincare, Ann.

nonlin. 15 (1998), 663-686.

[17] K.

ZHANG,

On various semiconvex hulls in the calculus of variations. Calc. Var. and

PDEs 6 (1998), 143-160.

[18] K.

ZHANG,

On the quasiconvex exposed points.

ESAIM:

Control Optim., Calc. Var.

6 (2001), 1-19.

The Richards equation for the modeling of a nuclear

waste repository

Olivier Lafitte and Christophe Le Potier

CEA/DM2S, Centre d'Etudes de Saclay

91191 Gif sur Yvette Cedex, France

E-mail : lafitte@math.polytechnique.fr

Abstract

We study a nonlinear degenerate parabolic equation (called the generalized

Richards equation) modeling the water pressure in a nuclear waste repository. We

show that this degenerate parabolic-elliptic equation has a unique solution, when

considering inhomogeneous Dirichlet boundary conditions induced by the surround-

ing geological material. We describe this solution (as in [2]) as the limit of a piecewise

linear function.

When studying a more general model taking into account the mechanical behav-

ior of the material, we show that the new equation on the water pressure h is a new

Richards equation, but no longer degenerate. We deduce that any model that will

take into account the mechanical behavior will be more regular than the Richards

equation.

1 Introduction

Modeling the saturation processes in a high level waste deep geological repository is a

crucial problem in the nuclear industry. This situation corresponds to the evolution of

the water flow in a saturated-instaturated medium. The equation used in this set-up is

the generalized Richards equation :

{9(h)) = C{h)d

h = div(K{h)Wh), (1)

which comes from the generalized Darcy's model

U = -K(h)Vh,

()

9{h) + div{U) = 0,

(

where h stands for the water pressure in the medium, 9(h) is the saturation and K(h) is

the permeability coefficient, see for example [8], [6], [4] for the justification of this model.

This model does not take into account the mechanical behavior of the material, which is

the aim of the third section of this paper.

152

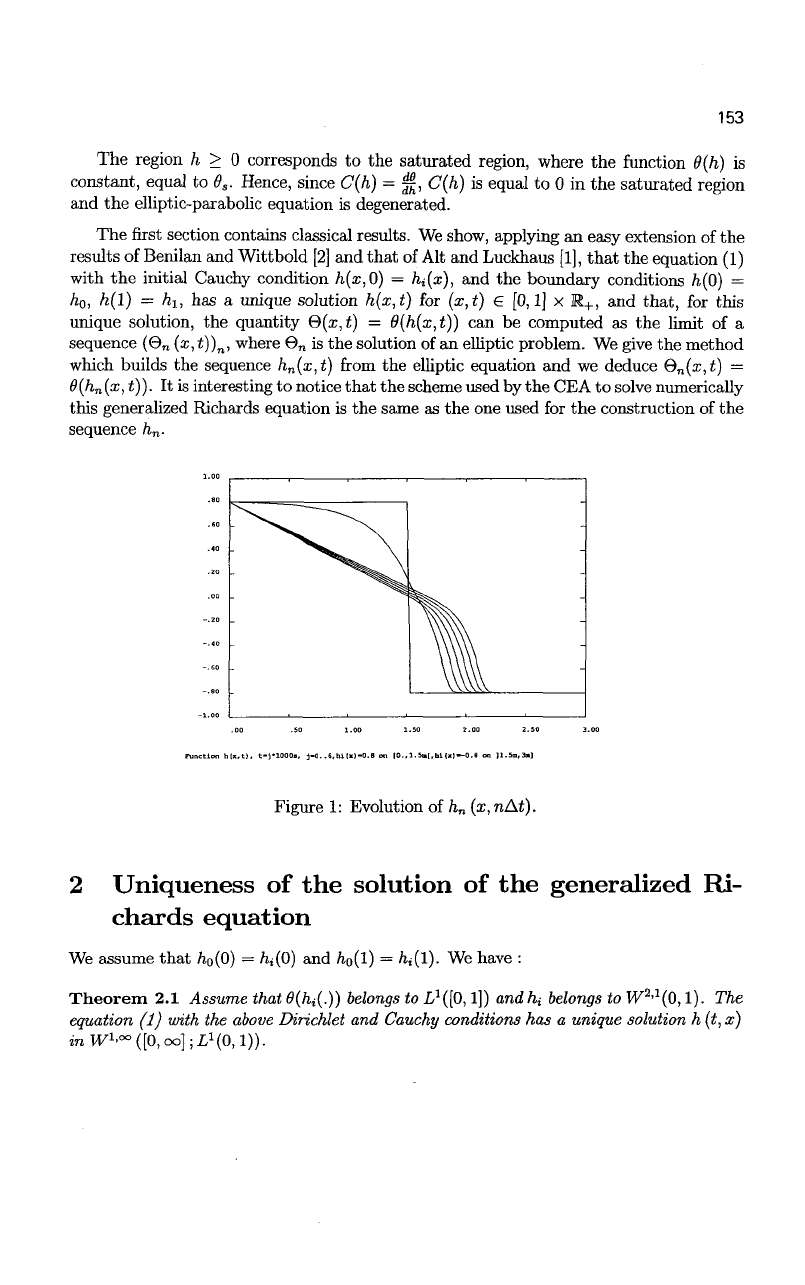
153

The region h > 0 corresponds to the saturated region, where the function 9(h) is

constant, equal to 6

. Hence, since C(h) = &, C(h) is equal to 0 in the saturated region

and the elliptic-parabolic equation is degenerated.

The first section contains classical results. We show, applying an easy extension of the

results of Benilan and Wittbold [2] and that of Alt and Luckhaus [1], that the equation (1)

with the initial Cauchy condition h(x,0) =

hi(x),

and the boundary conditions h(0) =

h(l) = hi, has a unique solution h(x,t) for (x,t) e [0,1] x K

, and that, for this

unique solution, the quantity Q(x,t) = 8(h(x,t)) can be computed as the limit of a

sequence (0„ (x, t))

, where Q„ is the solution of an elhptic problem. We give the method

which builds the sequence h

(x,t) from the elliptic equation and we deduce 0„(x,£) =

8(h

(x, t)). It is interesting to notice that the scheme used by the CEA to solve numerically

this generalized Richards equation is the same as the one used for the construction of the

sequence h

1.00

.80

-SO

-to

.00

-.20

-.ao

-.80

-1.00

.00 .50 1.00 1.50 2.00 2.50 3.00

Function h(x,t>, t-j*1000a, j-0. ,6,bl |«)-0.B m |0.,1.5a[,bl

Ul—

0.8 on ]1.5m,3n)

Figure 1: Evolution of h„ (x,nAt).

2 Uniqueness of the solution of the generalized Ri-

chards equation

We assume that h

{0) = M0) and h

(l) = hj(l). We have :

Theorem 2.1 Assume that 9(hi(.))

belongs

to ^([0,1]) andh

belongs to

1). The

equation (1) with the above Dirichlet and Cauchy conditions has a unique solution h (t, x)

in W

'™ {[0,oo};I?{0,l)).

154

The sketch of the proof is presented in [7]. We introduce : h

(x) = h

+ (hi - h

)x.

Under the assumption K(h) > C > 0, let us introduce Kirchoff's transform F of K :

rv+tm(x)

F(x,v)= / K(s)ds

The function v

\->

F(x,v) is strictly increasing. We denote by R(x,<fi) the function

such that F(x, R(x,

</>))

<p.

Notice that

{F(x, v(x,t) + ho(x))) = K {v(x,t) + h

{x)) (d

v(x,t) + d

(x)) - K(h

(x))(hi - h

Hence the equation (1) is equivalent to the following equation on v(x,t) = h(x,t)

—

(x) :

(0(v(x,t) + h

(x))) = d

(F(x,v(x,t))) + (hi - h

)-^(K{h

(x)))

and v satisfies the homogeneous Cauchy condition and the initial condition :

v(x,0) = hi(x) - h

(x).

We first show that the equation :

(F(x,v(x))) ~ (h - h

)^(K(h

(x))) = /(*), (3)

has a unique solution for / G i^QO, 1]) and that /

H->

V is increasing and continuous from

to W

. We thus introduce, for u e L^O, 1), the set

Au=

[ ~^

{F{x,v)) - (In - h

)±[K(h

(x))], v e W^ n Wo

, 1

u = 9(h

(x) +

v(x)).

For / in Au, we check that there exists v such that 9(ho(x) + v(x)) = u(x) and

f(x) = -^(^(*.«)) + d

(K(h

(x))).

This partial differential equation on v has a unique solution satisfying the homogeneous

Dirichlet boundary condition. Hence v constructed by the procedure is unique. This

proves the invertibility of A. The accretivity of A comes from the monotonicity of the

operator / i—> v. We thus prove the invertibility and accretivity of the multi-valued

operator A (in the sense described by Crandall and Ligget [3]). For all /, there exists

(through [3]) a unique (through Lemma 2.2) u in L

(0,1) such that / belongs to u + eAu,

e>0.

The main tool is the following Lemma.

Lemma 2.2 For v

G W

' , v'

G BV, the following assertions are equivalent :

155

• existence of v in L°°([0,

oo[;

n W

1,2

) such that 9{h

(x) + v(x,t)) belongs to

'°°([0, oo[; L

) and h

(x) + v(x,t) is a weak solution of (1), with the initial con-

dition : v{x, 0) = v

(x) (that is 9(h

(x) + v(x, 0)) = 0(fc/(x)) = 0i{x)),

• existence of a solution u in W

1,oo

([0,oo[;Z/

) such that 0 € u{t) + Au(t), a.e. and

u{0)=8(h

{x)).

The proof of this Lemma comes from the construction of a sequence approximating

the solution.

We thus construct the sequence

{x) = (I + eA)-

{x)) ; u°(x) = Oi(x).

We notice that this construction can be done as follows :

• find v\(x,t) solution of

8{vl{x) + h

(x)) - ei{x)

•

(F (x,vl(x))) + (h, - h

)£ (K (ho(x)))

• compute u\ (x) = 9{v\{x) + h

{x)) ;

• consider u\ instead of 8i(x) in the first step.

For e = 1/iV, we build u

(x,i) as the continuous function defined for t e [^, ^-] by

(x,t) = u$

{x) + {Nt - k)v*%{x).

As A is accretive, (u^(x,t))

converges, when N goes to infinity, to the same limit as

(7 + jjA)~ (9i). This limit is denoted by

u(x,t).

Denote by

v(x,t),

for almost every t,

the unique (through Lemma 2.2) solution of :

-d

,(F(x,v(x,t))) - (hi - ho)^{K{ho(x))) = ft«(a:.*)-

As0(u(x,t)+ho(a;)) = u(x,t) (using the definition of the limit), we check that h(x,t) =

v(x,t) + ho(x) is a solution of Richards' equation (1). As v(0,t) = v(l,t) = 0, by

construction, and v(x,0) = hi(x)

—

(x), h is a strong solution of the equation (1)

with h(0,i) = ho, h(l,t) = h\ and the initial condition 9(h(x,Q)) = 9(hi(x)). We thus

constructed h as this limit, and it is enough to construct v as the unique solution of (3)

to obtain the result of Lemma 2.2. •

Note that another initial condition gj(x) such that 9{hi{x)) = 9(gi(x)) leads to the

same solution h(x, t) of the problem on ]0, +oo[, through the uniqueness result.

We may also notice that the solution of this problem can be constructed in the following

way : introducing 0

n+1

(a;) = F(x,v

i(x)), we know that </>

n+1

(0) =

<j>„

i(l)

= 0 and

that :

156

-e^

(x) + 8(h

(x) + R(x,

</>

n+1

(x)))

= 9

(x) + efa - h

) — (K(h

(x))).

We have thus a fixed-end nonlinear elliptic equation. For each e, we build the sequence

(<p

(

))n

an<

i the- sequence {9

(x))

through :

{x) = 6{h

{x) + R{x,4>

{x))).

As before, let e = 1/N. The function 8

(x,t), which is continuous, piecewise linear

and equal to 6

(x) at t = n/N, converges to 8(x,t) and the unique solution of (1) is the

solution of Lemma 2.2 for f(x) = d

9(x,t).

This indeed proves the existence of the solution of the problem, and the uniqueness

comes from the results of Benilan and Wittbold for regular initial data. •

Note again that, in the above Figure 1, we gave a representation of h

(x, nAt) for

n = 0,..., 8 for a Van Genutchen model for 8(h) (see [6]).

3 Coupling with the mechanical behavior

The Richards equation was well studied by physicists, but it appears that it is not the

best equation to model a porous medium which is deformed under the pressure of a

liquid. Coupling Daxcy's law and the permeability law with the mechanical behavior of

the medium yields interesting results; in particular, the generalized Richards equation

obtained with this process is no longer a partial differential equation but can be seen as

a pseudo-differential equation, and it is no longer degenerate.

Recall that the displacement tensor e is given in terms of the stress tensor a through a

linear relation with constant coefficients, which is (i and j denote one of the coordinates)

= ^

( <>ii

i J

2(1 + 1/)

It is then easy to deduce the stress tensor in terms of the displacement (matrix D)

' (l-^eu + ^^T/r, ) ,

(l + */)(l-2z/)

0ii =

(1+ !/)(!-2«/) (2

""J

When we have air and water pressure in the medium (p

and p

) as well as other forces

6, the linear relation between the stress tensor, the water pressure p

and the deformation

tensor e is

157

da = D(de - h

d(p

- p

)),

1 (

where h

= — I * • We use the fundamental law of dynamics :

° \ 1 /

div

cr)

= -dtb,

dk , dk

dlj

to obtain the system on e and h = p

—p

. Using now e« = -^— and e;,- =

——

-—?-,

OTj era., oxi

obtain the following equation for the displacement (l

, l

= -d

b - h

dtVp

where K

is a matrix differential elliptic operator of order two and L

is a vector field

acting on d

- We use the relation between the porosity and the mechanical displacement

, l

), given by

+ djj. The total system is thus

' K

l + L

h = dt~b,

dt(8(h)) = ft(wS(/i))

= S(h)d

ui + u—o

= div{K(h)Vh), ^

u = ftTt(e)

= MB{x,V)d

= dt(dj

+ d

ly +

Note in this system that the function S(h) is the function 9(h) of the first part, the

notation considered depends on the physical problem studied. We have two ways of

rewriting the problem:

• The first approach uses the pseudo-differential calculus because the matricial linear

operator leads to a matricial symbol, and the calculus of K^

, where KT is elliptic,

is easier in this set-up. This system leads to the equation:

"IK ~

MB(

)^F

= div(K(h)Vh) - S(h)MB(x,V)K^d

~b.

In general, the operator R = UJ^

—

S(h)MB(x, V)K^

is a pseudo-differential

operator of order 0. When the Lame coefficients depend on the position (which may

be the case of a complicated geological structure), the pseudo-differential calculus

easily gives the leading order term of this zeroth-order operator.

'Note that it is not exactly the porosity as physically introduced, because in ti

we have u = gTre

and we omitted, for simplicity, the coefficient \ in the porosity given here.

158

The second more classical approach relies on the particular form of the operators and

of the constitutive relation of the material. In fact, considering the three equations

of the fundamental law of dynamics, and taking the divergence, we easily obtain

Jl^fc,-

h +

+ 9

div(6) = 0,

{l + u)(l-2u)

{l-2v)H

which implies that the function (

J)7

/)^

ai _

(i-L)H,^

oes no

^ depend on h,

hence the equality

{e{h))

= s{h)d

Lo~d

becomes, when d

—

ww-l-f +

irr^)**-^

Note that this equality becomes d

{6{h)) = L^f +

Ht(1

_„)ff(fe)] d

h+F when d = 2,

because we have

v°/

{l + v){\-2v)

/1\

\-2v

d = 2

d = 3.

Even in the region where S'(h) = 0 (which was the region where the Richards equation

was degenerate when the mechanical behavior was omitted) the coefficient of dh in the

equation (5) is greater than a constant equal to -=—

s~£7~>

where S

t is the constant

—

v) H

value of the function S(h) in the saturated region, equal to the minimum of S(h). We note

that the Richards equation without the mechanical behavior is u)—d

h = div(i

;

sr(/i)V/i) +

F, where a; is a constant. Hence the coefficient of d

h in this equation vanishes in the

saturated region, because S(h) is constant. Hence, when the mechanical behavior is

considered,

is non longer a constant as we saw and the elliptic-parabolic equation is

' dS 1

+ v .

h = div (K (h) V/i) + G,

159

where G is a source term. Introduce the function 0(h) such that :

"W-i+

££>>•

and h = 0

((7), with (0

)'(/t) < 1/C

and the equation (5) writes

U = d&(B(U)) + G,

which is a non-linear non degenerate elliptic parabolic equation.

A similar idea was used by Le Potier [6] in the numerical computation of the solution

of the coupled problem, splitting the term

S(h)d

into two terms, one being positive and

h (

leading to a non-degenerate Richards equation. Precisely, he writes d

e —— 1 I =

<J.

Hence using to = Tr(e) and d

cr = -MB (z,V)

K^dtib),

he obtains a new

system, where the modified Richards equation has a "mechanical" source term and a non

vanishing coefficient for the term d

h, which is w— +

—S(h).

It is still a coupled system

ah H

(because a depends on h and is still in the equation for h), but the coefficient of d

h is

positive, and a usual numerical method for the heat equation is convenient in most cases.

References

[1] H.W.Alt, S. Luckhaus, Quasilinear elliptic-parabolic differential equations. Math. Z.

183 (1983),

311-341.

[2] P. Benilan, P. Wittbold, Sur un modele parabolique-elliptique. Math. Mod. Num.

Anal. M2AN 33(1) (1999), 121-127.

[3] M.G. Crandall, T. Liggett, Generation of semigroups of nonlinear transformations on

general Banach spaces. Amer. J. Math. 93 (1971), 265-298.

[4] P.S. Huyakorn, G. F. Pinder, Computational methods in Subsurface Flow. Academic

Press,

New York, 1983.

[5] J. Kacur, Solution of some free boundary problems by relaxation schemes. SIAM J.

Numer. Anal. 36(1) (1999), 290-316.

[6] C. Le Potier, F. Cany, Couplage hydromecanique et transferts de gaz dans les milieux

poreux. Rapport DMT/SEMT/MTMS/RT/00-115+ du 5/12/2000.

[7] O. Lafitte, C. Le Potier, Quelques remarques sur le couplage du transfert hydrique

et du comportement mecanique en milieu poreux. Rapport DM2S/SFME/MTMS/01-

005Mars 2001.

[8] G. de Marshy, Quantitative

Hydrogeology.

Academic Press, New York, 1986.