Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
597
*9.11 BENDING-MOMENT DIAGRAMS BY PARTS
In many applications the determination of the angle u
DyC
and of the
tangential deviation t
DyC
is simplified if the effect of each load is
evaluated independently. A separate (MyEI) diagram is drawn for
each load, and the angle u
DyC
is obtained by adding algebraically the
areas under the various diagrams. Similarly, the tangential deviation
t
DyC
is obtained by adding the first moments of these areas about a
vertical axis through D. A bending-moment or (MyEI) diagram plot-
ted in this fashion is said to be drawn by parts.
When a bending-moment or (MyEI) diagram is drawn by parts,
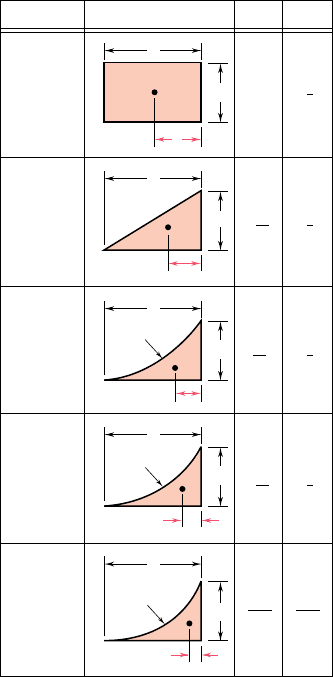
the various areas defined by the diagram consist of simple geometric
shapes, such as rectangles, triangles, and parabolic spandrels. For
convenience, the areas and centroids of these various shapes have
been indicated in Fig. 9.48.
9.11 Bending-Moment Diagrams by Parts
Shape Area c
b
b
3
Rectangle
Triangle
Parabolic
spandrel
Cubic
spandrel
General
spandrel
b
2
bh
bh
2
c
h
b
C
C
c
h
b
4
bh
3
b
C
c
h
b
5
bh
4
bh
n 1
b
n 2
y kx
2
b
C
c
h
y kx
3
b
C
c
h
y kx
n
Fig. 9.48 Areas and centroids of common
shapes.
bee80288_ch09_548-629.indd Page 597 10/30/10 11:24:01 PM user-f499bee80288_ch09_548-629.indd Page 597 10/30/10 11:24:01 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
598
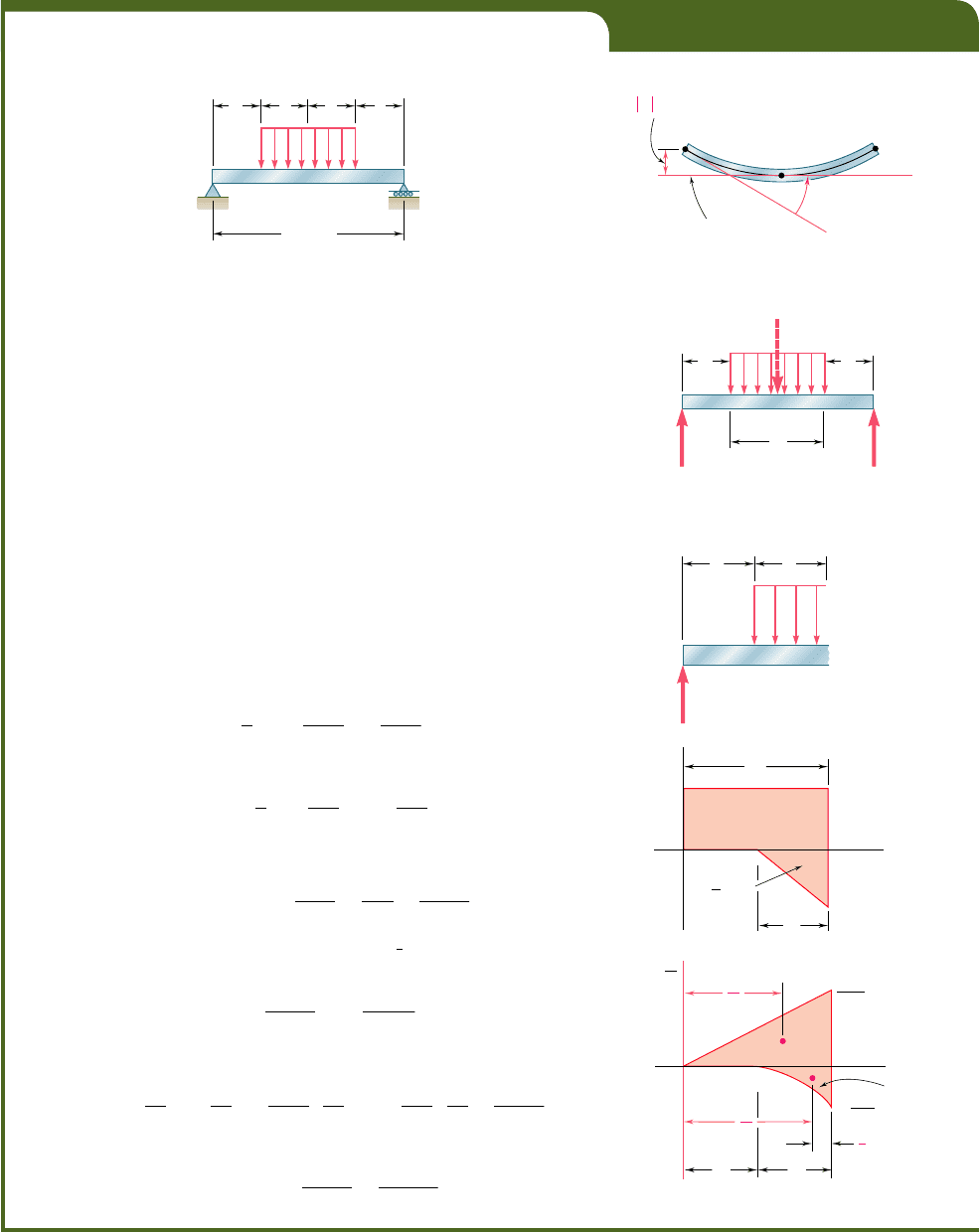
EXAMPLE 9.10
Determine the slope and deflection at end B of the prismatic beam of
Example 9.09, drawing the bending-moment diagram by parts.
We replace the given loading by the two equivalent loadings shown
in Fig. 9.49, and draw the corresponding bending-moment and (MyEI)
diagrams from right to left, starting at the free end B.
Applying the first moment-area theorem, and recalling that u
A
5 0,
we write
u
B
5 u
B
y
A
5
A
1
1
A
2
5
1
9 3 10
23
m
21
21
3 m
2
2
1
2
1
15 3 10
23
m
21
21
3 m
2
5 27 3 10
2
3
2 22.5 3 10
2
3
5 4.5 3 10
2
3
rad
Applying the second moment-area theorem, we compute the first moment
of each area about a vertical axis through B and write
y
B
5 t
B
y
A
5 A
1
1
1.5 m
2
1 A
2
1
2 m
2
5
1
27 3 10
2
3
21
1.5 m
2
2
1
22.5 3 10
2
3
21
2 m
2
5 40
.
5 mm 2 45 mm 524
.
5 mm
It is convenient, in practice, to group into a single drawing the two por-
tions of the (MyEI) diagram (Fig. 9.50).
3 m
AB
50 kN
90 kN · m
90 kN · m
3 m
3 m
3 m
1.5 m
2 m
150 kN · m
15 10
3
m
1
9 10
3
m
1
M
A
M
A
BA
BB
xx
A
1
A
2
A
B
A
B
xx
A
B
90 kN · m
M
EI
M
EI
50 kN
Fig. 9.49
3 m
1.5 m
2 m
15 10
3
m
1
9 10
3
m
1
A
A
1
A
2
B
x
M
EI
Fig. 9.50
bee80288_ch09_548-629.indd Page 598 11/18/10 8:57:52 PM user-f499bee80288_ch09_548-629.indd Page 598 11/18/10 8:57:52 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
599
EXAMPLE 9.11
For the prismatic beam AB and the loading shown (Fig. 9.51), determine
the slope at a support and the maximum deflection.
We first sketch the deflected beam (Fig. 9.52). Since the tangent at the
center C of the beam is horizontal, it will be used as the reference tangent,
and we have |y|
max
5 t
AyC
. On the other hand, since u
C
5 0, we write
u
C
y
A
5
u
C
2
u
A
52
u
A
or
u
A
52
u
C
y
A
From the free-body diagram of the beam (Fig. 9.53), we find that
R
A
5 R
B
5 wa
Next, we draw the shear and bending-moment diagrams for the portion
AC of the beam. We draw these diagrams by parts, considering separately
the effects of the reaction R
A
and of the distributed load. However, for
convenience, the two parts of each diagram have been plotted together
(Fig. 9.54). We recall from Sec. 5.3 that, the distributed load being uni-
form, the corresponding parts of the shear and bending-moment diagrams
will be, respectively, linear and parabolic. The area and centroid of the
triangle and of the parabolic spandrel can be obtained by referring to
Fig. 9.48. The areas of the triangle and spandrel are found to be,
respectively,
A
1
5
1
2
12a2
a
2wa
2
EI
b
5
2wa
3
EI
and
A
2
52
1
3
1a2
a
wa
2
2EI
b
52
wa
3
6EI
Applying the first moment-area theorem, we write
u
C
y
A
5 A
1
1 A
2
5
2wa
3
EI
2
wa
3
6EI
5
11wa
3
6EI
Recalling from Figs. 9.51 and 9.52 that
a
5
1
4
L and u
A
5 2u
CyA
, we
have
u
A
52
11wa
3
6EI
52
11wL
3
384EI
Applying now the second moment-area theorem, we write
t
A
y
C
5 A
1
4a
3
1 A
2
7a
4
5
a
2wa
3
EI
b
4a
3
1
a
2
wa
3
6EI
b
7a
4
5
19wa
4
8EI
and
0y0
max
5 t
A
y
C
5
19wa
4
8EI
5
19wL
4
2048EI
Fig. 9.51
aaaa
w
A
DE
B
C
L 4a
B
A
A
C
B
Reference tangent
C/A
y
max
t
A/C
Fig. 9.52
a
2wa
A
R
A
R
B
DE
B
C
B
a
2a
Fig. 9.53
a
(2wa
2
)
w
A
V
R
A
wa
R
A
wa
wa
( wa
2
)
D
C
x
D
A
C
a
a
a
a
a
2a
1
2
A
A
1
A
2
wa
2
D
C
x
M
EI
2 wa
2
2 EI
EI
4a
3
7a
4
1
4
Fig. 9.54
bee80288_ch09_548-629.indd Page 599 11/1/10 8:40:09 PM user-f499bee80288_ch09_548-629.indd Page 599 11/1/10 8:40:09 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
600
SAMPLE PROBLEM 9.10
The prismatic rods AD and DB are welded together to form the cantilever
beam ADB. Knowing that the flexural rigidity is EI in portion AD of the
beam and 2EI in portion DB, determine, for the loading shown, the slope
and deflection at end A.
SOLUTION
(MyEI) Diagram. We first draw the bending-moment diagram for the
beam and then obtain the (MyEI) diagram by dividing the value of M at
each point of the beam by the corresponding value of the flexural rigidity.
Reference Tangent. We choose the horizontal tangent at the fixed end
B as the reference tangent. Since u
B
5 0 and y
B
5 0, we note that
u
A
52
u
B
y
A
y
A
5 t
A
y
B
A
a
D
EI
2EI
a
P P
B
A
V
P
Pa
2P
3Pa
Pa
B
M
x
x
x
x
D
EI
EI
2EI
2EI
R
B
M
B
M
EI
Pa
EI
3Pa
2EI
P P
Reference tangent
B/A
A
A
B
y
A
t
A/B
aa
B
A
a
D
A
2
A
3
A
1
Pa
x
2EI
M
EI
Pa
EI
3Pa
2EI
5
3
a
4
3
a
2
3
Slope at A. Dividing the (MyEI) diagram into the three triangular
portions shown, we write
A
1
52
1
2
Pa
EI
a 52
Pa
2
2EI
A
2
52
1
2
Pa
2EI
a 52
Pa
2
4EI
A
3
52
1
2
3Pa
2EI
a 52
3Pa
2
4EI
Using the first moment-area theorem, we have
u
B
y
A
5 A
1
1 A
2
1 A
3
52
Pa
2
2EI
2
Pa
2
4EI
2
3Pa
2
4EI
52
3Pa
2
2EI
u
A
52u
B
y
A
51
3Pa
2
2E
I
u
A
5
3Pa
2
2E
I
a b
Deflection at A. Using the second moment-area theorem, we have
y
A
5 t
A
y
B
5 A
1
a
2
3
a
b
1 A
2
a
4
3
a
b
1 A
3
a
5
3
a
b
5
a
2
Pa
2
2EI
b
2a
3
1
a
2
Pa
2
4EI
b
4a
3
1
a
2
3Pa
2
4EI
b
5a
3
y
A
52
23Pa
3
12EI
y
A
5
23Pa
3
12E
I
w b
bee80288_ch09_548-629.indd Page 600 11/1/10 8:40:20 PM user-f499bee80288_ch09_548-629.indd Page 600 11/1/10 8:40:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
601
SAMPLE PROBLEM 9.11
For the prismatic beam and loading shown, determine the slope and deflec-
tion at end E.
SOLUTION
(MyEI) Diagram. From a free-body diagram of the beam, we deter-
mine the reactions and then draw the shear and bending-moment diagrams.
Since the flexural rigidity of the beam is constant, we divide each value of
M by EI and obtain the (MyEI) diagram shown.
Reference Tangent. Since the beam and its loading are symmetric
with respect to the midpoint C, the tangent at C is horizontal and is used
as the reference tangent. Referring to the sketch, we observe that, since
u
C
5 0,
u
E
5
u
C
1
u
E
y
C
5
u
E
y
C
(1)
y
E
5 t
E
y
C
2 t
D
y
C
(2)
Slope at E. Referring to the (MyEI) diagram and using the first
moment-area theorem, we write
A
1
52
wa
2
2EI
a
L
2
b
52
wa
2
L
4EI
A
2
52
1
3
a
wa
2
2EI
b
1a252
wa
3
6EI
Using Eq. (1), we have
u
E
5 u
E
y
C
5 A
1
1 A
2
52
wa
2
L
4EI
2
wa
3
6EI
u
E
52
wa
2
12EI
13L 1 2a2
u
E
5
wa
2
12E
I
13L 1 2a2
c b
Deflection at E. Using the second moment-area theorem, we write
t
D
y
C
5 A
1
L
4
5
a
2
wa
2
L
4EI
b
L
4
52
wa
2
L
2
16EI
t
E
y
C
5 A
1
a
a 1
L
4
b
1 A
2
a
3a
4
b
5
a
2
wa
2
L
4EI
b
a
a 1
L
4
b
1
a
2
wa
3
6EI
b
a
3a
4
b
52
wa
3
L
4EI
2
wa
2
L
2
16EI
2
wa
4
8EI
Using Eq. (2), we have
y
E
5 t
E
y
C
2 t
D
y
C
52
wa
3
L
4EI
2
wa
4
8EI
y
E
52
wa
3
8EI
12L 1 a2
y
E
5
wa
3
8EI
12L 1 a2
w b
B
A
L
CD
E
2
a
L
a
ww
B
A
CD
E
A
1
A
2
L
a
V
x
x
x
M
a
a
wa
wa
wa
2
2
L
2
wa
2
2EI
wa
2
2EI
3a
4
a
4
wa
2
2
L
4
M
EI
R
B
wa R
D
wa
w w
B
A
C
y
E
E
E
D
Reference tangent
t
D/C
t
E/C
bee80288_ch09_548-629.indd Page 601 11/1/10 9:34:12 PM user-f499bee80288_ch09_548-629.indd Page 601 11/1/10 9:34:12 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
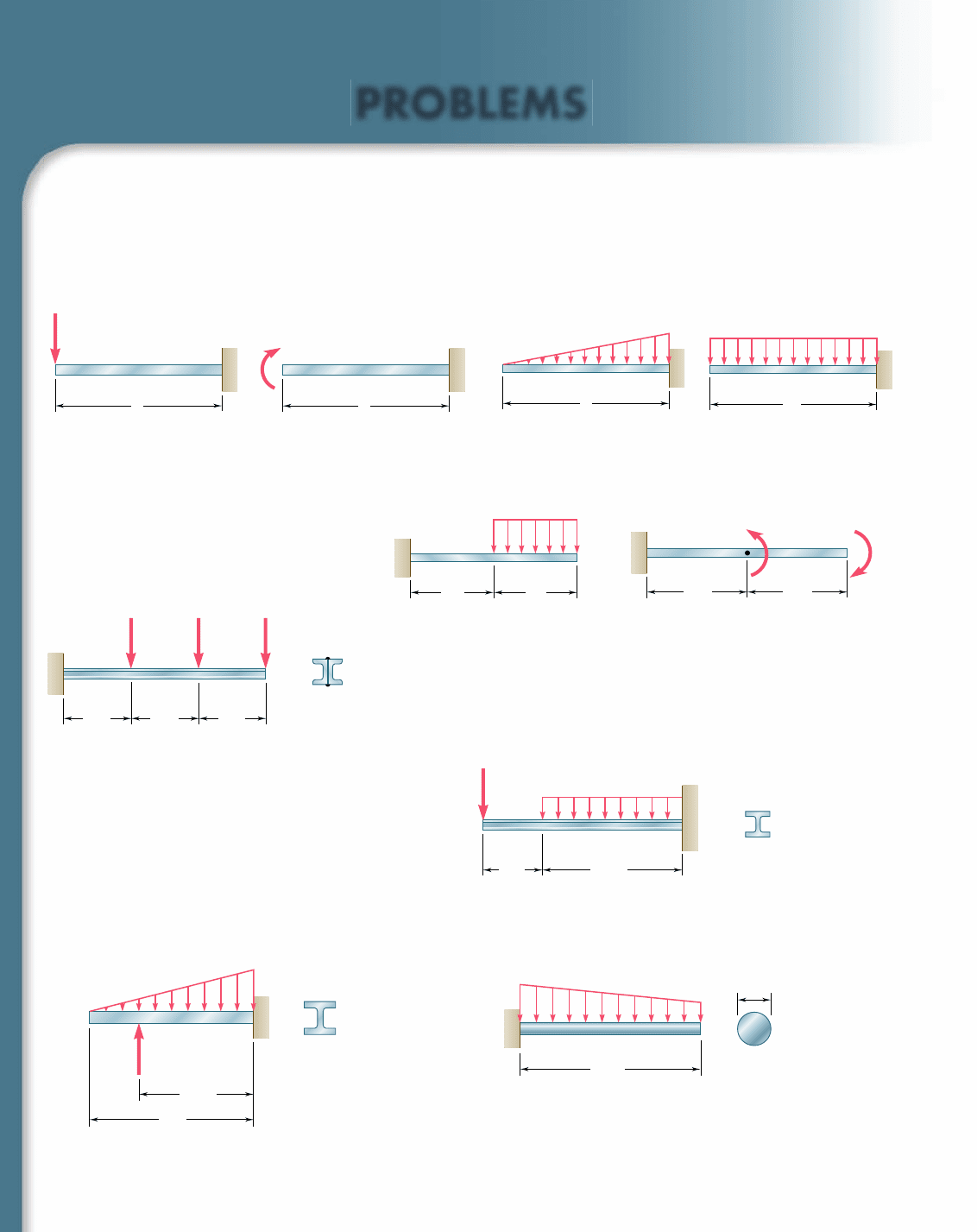
PROBLEMS
602
Use the moment-area method to solve the following
problems.
9.95 through 9.98 For the uniform cantilever beam and loading
shown, determine (a) the slope at the free end, (b) the deflection
at the free end.
L
A
B
P
Fig. P9.95
M
0
L
A
B
Fig. P9.96
B
w
L
A
Fig. P9.98
B
A
w
0
L
Fig. P9.97
9.99 and 9.100 For the uniform cantilever beam and loading shown,
determine the slope and deflection at (a) point B, (b) point C.
L/2 L/2
A
B
C
w
Fig. P9.99
2M
0
M
0
B
A
C
L/2 L/2
Fig. P9.100
9.101 Two C6 3 8.2 channels are welded back to back and loaded as
shown. Knowing that E 5 29 3 10
6
psi, determine (a) the slope
at point D, (b) the deflection at point D.
9.102 For the cantilever beam and loading shown, determine (a) the slope
at point A, (b) the deflection at point A. Use E 5 200 GPa.
D
A
CB
2 ft 2 ft 2 ft
C6 8.2
1.1 kips 1.1 kips 1.1 kips
Fig. P9.101
A
4 kN/m
C
B
1 m
2.5 m
W250 22.3
5 kN
Fig. P9.102
9.103 For the cantilever beam and loading shown, determine (a) the slope
at point B, (b) the deflection at point B. Use E 5 29 3 10
6
psi.
1.8 in.
30 in.
B
A
40 lb/in.
100 lb/in.
Fig. P9.103
3 m
2.1 m
A
BC
20 kN
120 kN/m
W360 64
Fig. P9.104
9.104 For the cantilever beam and loading shown, determine (a) the slope
at point A, (b) the deflection at point A. Use E 5 200 GPa.
bee80288_ch09_548-629.indd Page 602 10/30/10 11:24:37 PM user-f499bee80288_ch09_548-629.indd Page 602 10/30/10 11:24:37 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
603
Problems
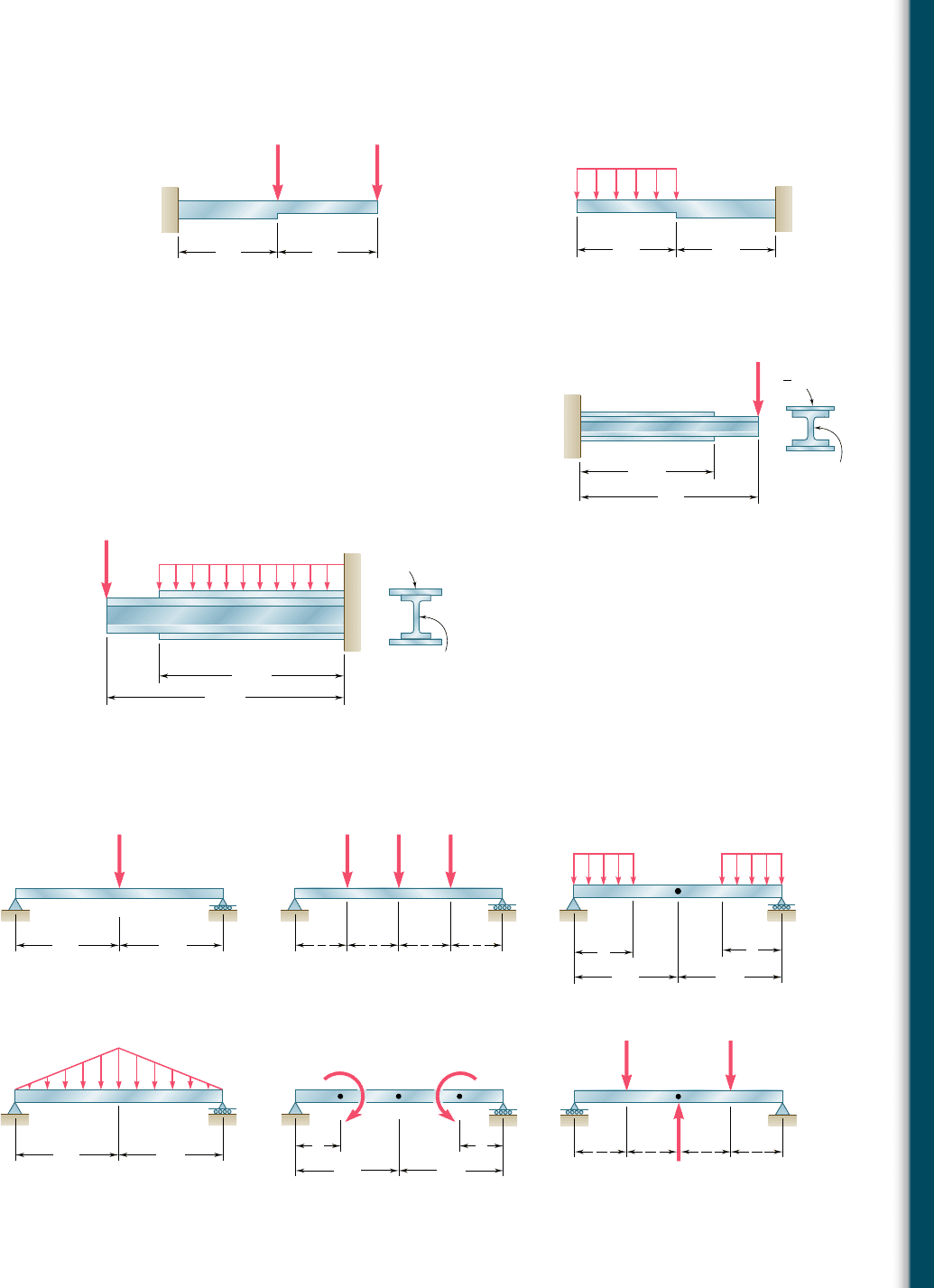
9.105 For the cantilever beam and loading shown, determine (a) the
slope at point C, (b) the deflection at point C.
B
A
C
L/2
1.5EI EI
L/2
PP
Fig. P9.105
A
BC
3EI
EI
L/2L/2
w
Fig. P9.106
9.106 For the cantilever beam and loading shown, determine (a) the
slope at point A, (b) the deflection at point A.
9.107 Two cover plates are welded to the rolled-steel beam as shown.
Using E 5 29 3 10
6
psi, determine (a) the slope at end C, (b) the
deflection at end C.
9.108 Two cover plates are welded to the rolled-steel beam as shown.
Using E 5 200 GPa, determine (a) the slope at end A, (b) the
deflection at end A.
W10 45
4.5 ft
6 ft
15 kips
A
BC
9 in.
1
2
Fig. P9.107
A
90 kN/m
C
B
2.1 m
2.7 m
W410 60
12 200 mm
40 kN
Fig. P9.108
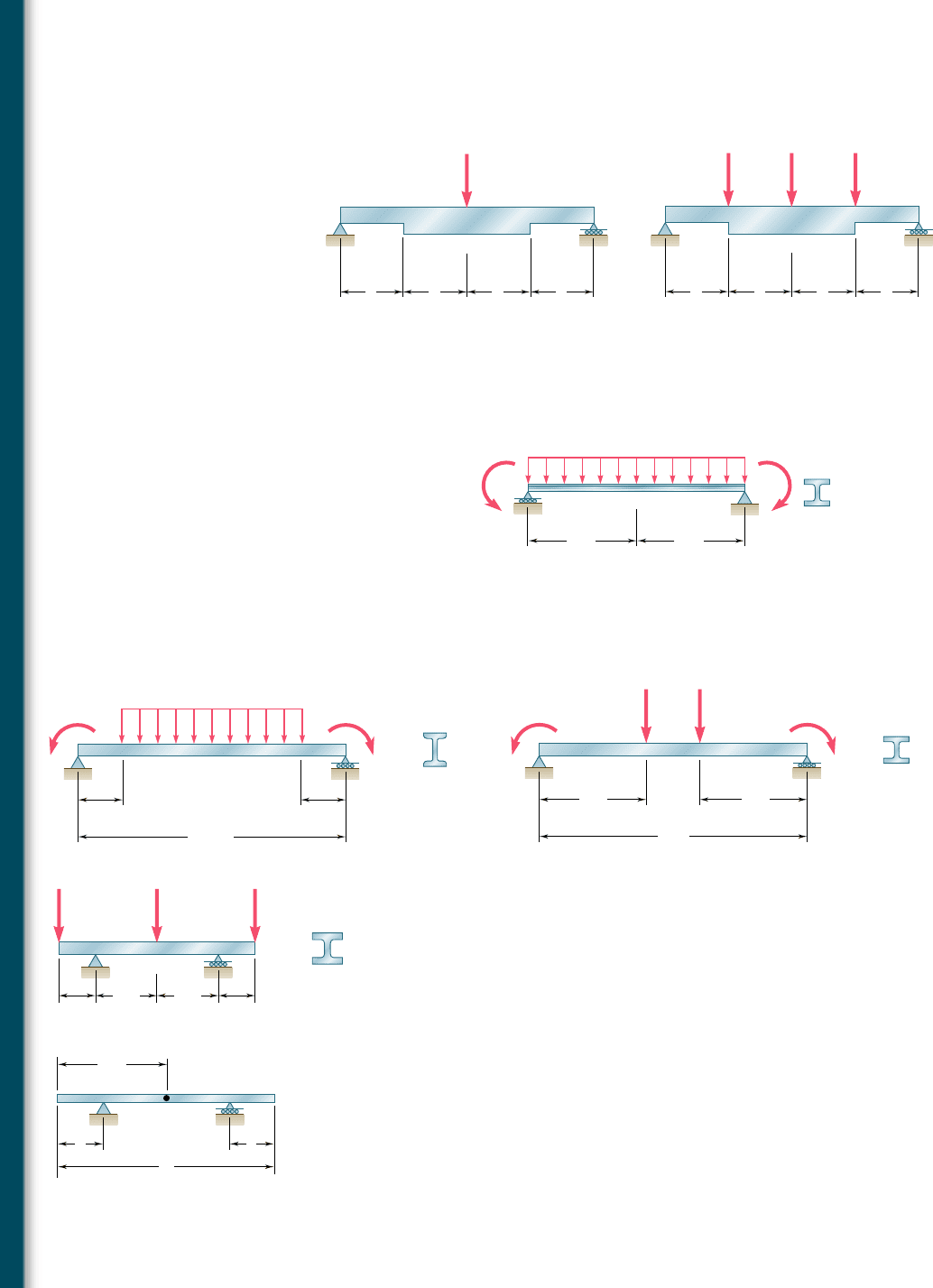
9.109 through 9.114 For the prismatic beam and loading shown,
determine (a) the slope at end A, (b) the deflection at the center
C of the beam.
Fig . P 9.111
A
a
a
E
CDB
L/2L/2
w
w
A
B
E
CD
L
4
L
4
L
4
L
4
P
P
P
Fig. P9.114
A
aa
E
C
D
B
M
0
M
0
L/2L/2
Fig. P9.113
A
B
C
w
0
L/2L/2
Fig. P9.112
A
L
C
E
B
P
D
4
L
4
L
4
L
4
P P
Fig. P9.110
A
L/2L/2
C
B
P
Fig. P9.109
bee80288_ch09_548-629.indd Page 603 11/1/10 8:40:39 PM user-f499bee80288_ch09_548-629.indd Page 603 11/1/10 8:40:39 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
604
Defl ection of Beams
9.115 and 9.116 For the beam and loading shown, determine (a) the
slope at end A, (b) the deflection at the center C of the beam.
A
DCB
E
2EI
a
EIEI
P
a a a
Fig. P9.115
A
D
CB
E
3EI
a
EIEI
a a a
P P2P
Fig. P9.116
9.117 For the beam and loading shown and knowing that w 5 8 kN/m,
determine (a) the slope at end A, (b) the deflection at midpoint C.
Use E 5 200 GPa.
A
5 m 5 m
B
C
40 kN · m 40 kN · m
W310 60
w
Fig. P9.117
9.118 and 9.119 For the beam and loading shown, determine (a) the
slope at end A, (b) the deflection at the midpoint of the beam. Use
E 5 200 GPa.
0.6 m
A
E
BD
10 kN · m 10 kN · m
40 kN/m
0.6 m
3.6 m
S250 37.8
Fig. P9.118
60 kN · m
150 kN
60 kN · m
150 kN
2 m 2 m
5 m
W460 74
AE
BD
Fig. P9.119
9.120 Knowing that P 5 4 kips, determine (a) the slope at end A, (b) the
deflection at the midpoint C of the beam. Use E 5 29 3 10
6
psi.
9.121 For the beam and loading of Prob. 9.117, determine the value of
w for which the deflection is zero at the midpoint C of the beam.
Use E 5 200 GPa.
9.122 For the beam and loading of Prob. 9.120, determine the magnitude
of the forces P for which the deflection is zero at end A of the
beam. Use E 5 29 3 10
6
psi.
*9.123 A uniform rod AE is to be supported at two points B and D. Deter-
mine the distance a for which the slope at ends A and E is zero.
*9.124 A uniform rod AE is to be supported at two points B and D. Deter-
mine the distance a from the ends of the rod to the points of support,
if the downward deflections of points A, C, and E are to be equal.
W8 13
5 kipsPP
3 ft
3 ft
5 ft5 ft
A
BD
E
C
Fig. P9.120
A
a
a
L
E
L/2
C
B
D
Fig. P9.123 and P9.124
bee80288_ch09_548-629.indd Page 604 11/18/10 8:57:57 PM user-f499bee80288_ch09_548-629.indd Page 604 11/18/10 8:57:57 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
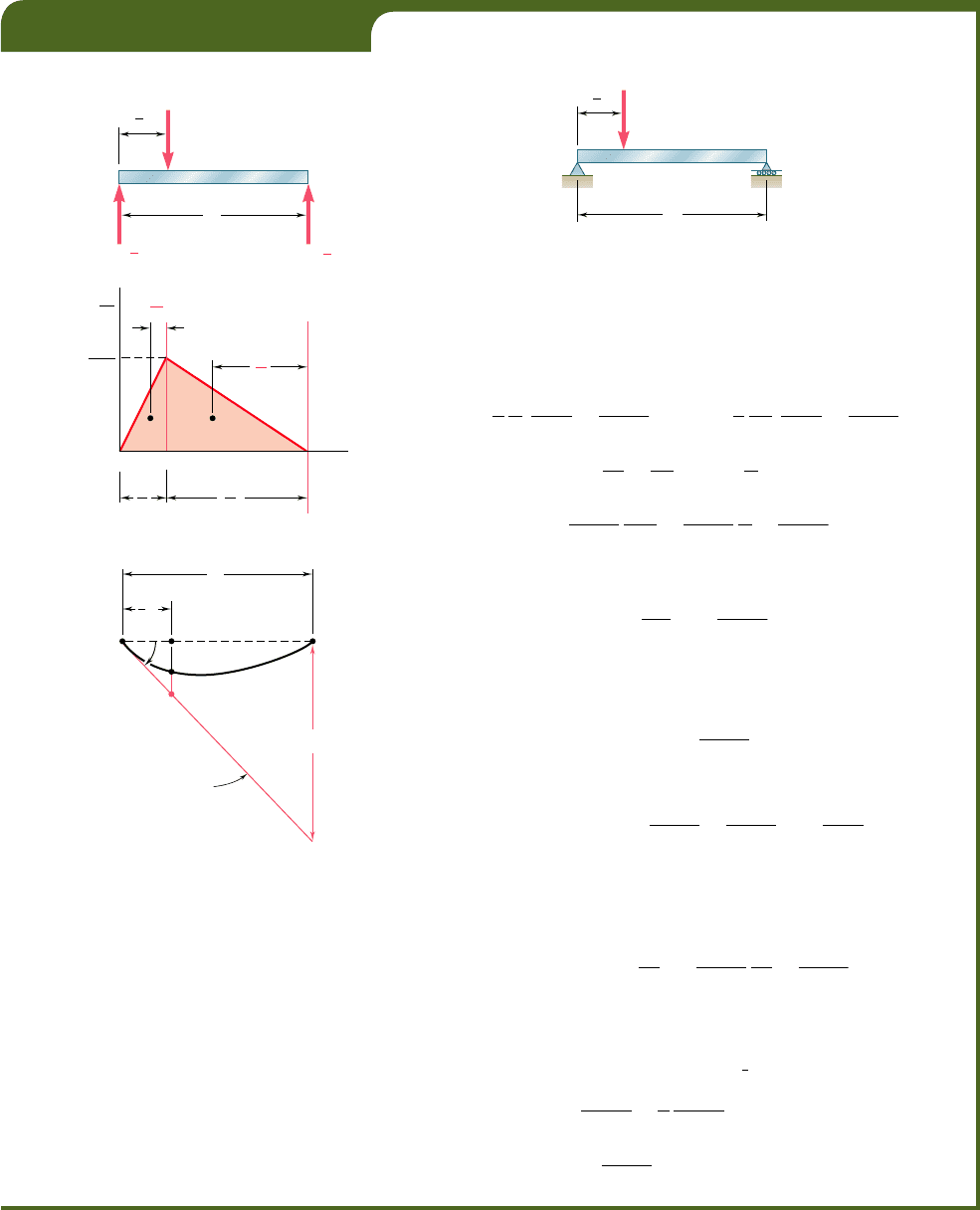
*9.12 APPLICATION OF MOMENT-AREA THEOREMS
TO BEAMS WITH UNSYMMETRIC LOADINGS
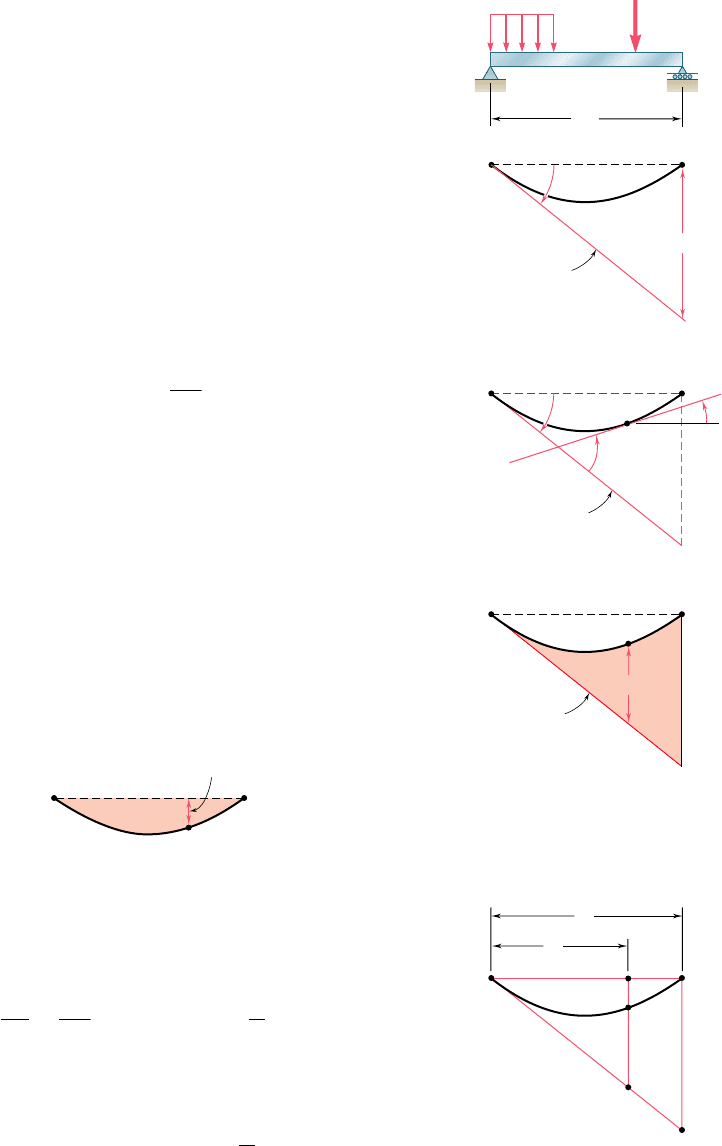
We saw in Sec. 9.10 that, when a simply supported or overhanging
beam carries a symmetric load, the tangent at the center C of the
beam is horizontal and can be used as the reference tangent. When
a simply supported or overhanging beam carries an unsymmetric load,
it is generally not possible to determine by inspection the point of
the beam where the tangent is horizontal. Other means must then be
found for locating a reference tangent, i.e., a tangent of known slope
to be used in applying either of the two moment-area theorems.
It is usually most convenient to select the reference tangent at
one of the beam supports. Considering, for example, the tangent at
the support A of the simply supported beam AB (Fig. 9.55), we
determine its slope by computing the tangential deviation t
ByA
of the
support B with respect to A, and dividing t
ByA
by the distance L
between the supports. Recalling that the tangential deviation of a
point located above the tangent is positive, we write
u
A
52
t
B
y
A
L
(9.61)
Once the slope of the reference tangent has been found, the
slope u
D
of the beam at any point D (Fig. 9.56) can be determined
by using the first moment-area theorem to obtain u
DyA
, and then
writing
u
D
5 u
A
1 u
D
y
A
(9.62)
The tangential deviation t
DyA
of D with respect to the support
A can be obtained from the second moment-area theorem. We note
that t
DyA
is equal to the segment ED (Fig. 9.57) and represents the
vertical distance of D from the reference tangent. On the other
hand, the deflection y
D
of point D represents the vertical distance
of D from the horizontal line AB (Fig. 9.58). Since y
D
is equal in
605
9.12 Application of Moment-Area Theorems
to Beams with Unsymmetric Loadings
P
Reference
tangent
A
w
B
A
B
L
(a)
(b)
A
t
B/A
Fig. 9.55
D
A
D/A
D
Reference
tangent
B
A
Fig. 9.56
t
D/A
D
E
B
A
Reference
tangent
Fig. 9.57
D
F
y
D
B
A
Fig. 9.58
magnitude to the segment FD, it can be expressed as the difference
between EF and ED (Fig. 9.59). Observing from the similar trian-
gles AFE and ABH that
EF
x
5
HB
L
or
EF 5
x
L
t
B
y
A
and recalling the sign conventions used for deflections and tangential
deviations, we write
y
D
5 ED 2 EF 5 t
D
y
A
2
x
L
t
B
y
A
(9.63)
t
B/A
D
E
H
x
L
F
B
A
Fig. 9.59
bee80288_ch09_548-629.indd Page 605 11/18/10 8:58:13 PM user-f499bee80288_ch09_548-629.indd Page 605 11/18/10 8:58:13 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
EXAMPLE 9.12
For the prismatic beam and loading shown (Fig. 9.60), determine the
slope and deflection at point D.
B
D
L
L
P
A
1
4
Fig. 9.60
Reference Tangent at Support A. We compute the reactions at
the supports and draw the (MyEI) diagram (Fig. 9.61). We determine the
tangential deviation t
ByA
of the support B with respect to the support A
by applying the second moment-area theorem and computing the moments
about a vertical axis through B of the areas A
1
and A
2
. We have
A
1
5
1
2
L
4
3PL
16EI
5
3PL
2
128EI
A
2
5
1
2
3L
4
3PL
16EI
5
9PL
2
128EI
t
B
y
A
5 A
1
a
L
12
1
3L
4
b
1 A
2
a
L
2
b
5
3PL
2
128EI
10L
12
1
9PL
2
128EI
L
2
5
7PL
3
128EI
The slope of the reference tangent at A (Fig. 9.62) is
u
A
52
t
B
y
A
L
52
7PL
2
128EI
Slope at D. Applying the first moment-area theorem from A to
D, we write
u
D
y
A
5 A
1
5
3PL
2
128EI
Thus, the slope at D is
u
D
5 u
A
1 u
D
y
A
52
7PL
2
128EI
1
3PL
2
128EI
52
PL
2
32EI
Deflection at D. We first determine the tangential deviation DE 5
t
DyA
by computing the moment of the area A
1
about a vertical axis
through D:
DE 5 t
D
y
A
5 A
1
a
L
12
b
5
3PL
2
128EI
L
12
5
PL
3
512EI
The deflection at D is equal to the difference between the segments DE
and EF (Fig. 9.62). We have
y
D
5 DE 2 EF 5 t
D
y
A
2
1
4
t
B
y
A
5
PL
3
512EI
2
1
4
7PL
3
128EI
y
D
52
3PL
3
256EI
520.01172PL
3
/EI
12
B
D
L
A
1
A
2
AD B
x
L
2
L
4
L
4
3L
EI
M
16EI
3PL
L
P
A
1
4
R
B
P
4
R
A
P
3
4
Fig. 9.61
L
Reference
tangent
F
E
t
B/A
D
A
A
B
L
1
4
Fig. 9.62
606
bee80288_ch09_548-629.indd Page 606 11/1/10 8:41:03 PM user-f499bee80288_ch09_548-629.indd Page 606 11/1/10 8:41:03 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
