Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

567

Problems

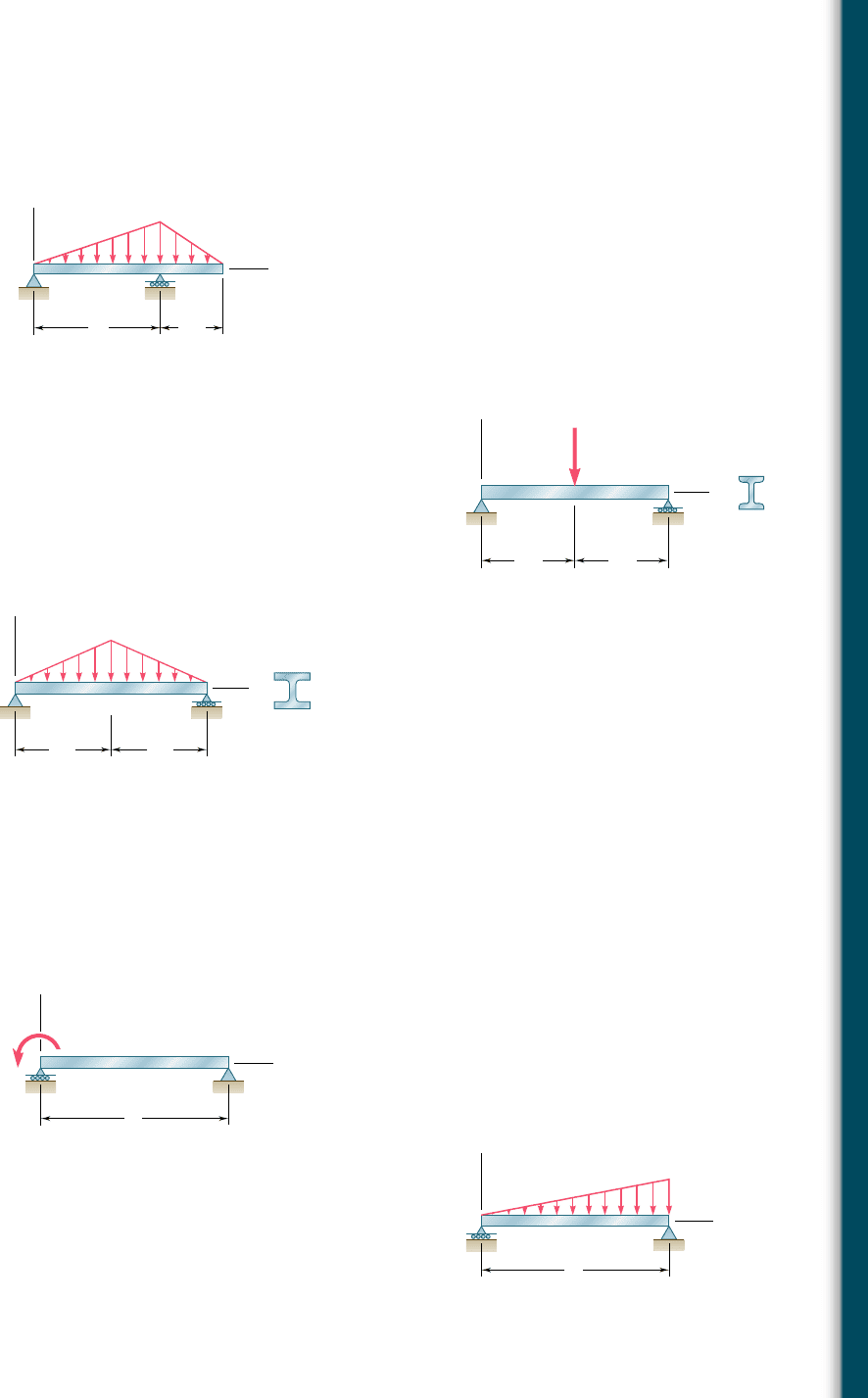
9.8 For the beam and loading shown, determine (a) the equation of

the elastic curve for portion AB of the beam, (b) the deflection at

midspan, (c) the slope at B.

9.11 (a) Determine the location and magnitude of the maximum deflec-

tion of beam AB. (b) Assuming that beam AB is a W360 3 64, L 5

3.5 m, and E 5 200 GPa, calculate the maximum allowable value of

the applied moment M

if the maximum deflection is not to exceed

1 mm.

LL/2

Fig. P9.8

9.9 Knowing that beam AB is an S200 3 34 rolled shape and that P 5

60 kN, L 5 2 m, and E 5 200 GPa, determine (a) the slope at A,

(b) the deflection at C.

9.10 Knowing that beam AB is a W10 3 33 rolled shape and that w

3 kips/ft, L 5 12 ft, and E 5 29 3 10

psi, determine (a) the slope

at A, (b) the deflection at C.

L/2

Fig. P9.9

L/2 L/2

Fig. P9.10

9.12 For the beam and loading shown, (a) express the magnitude and

location of the maximum deflection in terms of w

, L, E, and I.

(b) Calculate the value of the maximum deflection, assuming that

beam AB is a W18 3 50 rolled shape and that w

5 4.5 kips/ft,

L 5 18 ft, and E 5 29 3 10

psi.

Fig. P9.11

Fig. P9.12

bee80288_ch09_548-629.indd Page 567 11/18/10 8:56:25 PM user-f499bee80288_ch09_548-629.indd Page 567 11/18/10 8:56:25 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

568

Deﬂ ection of Beams

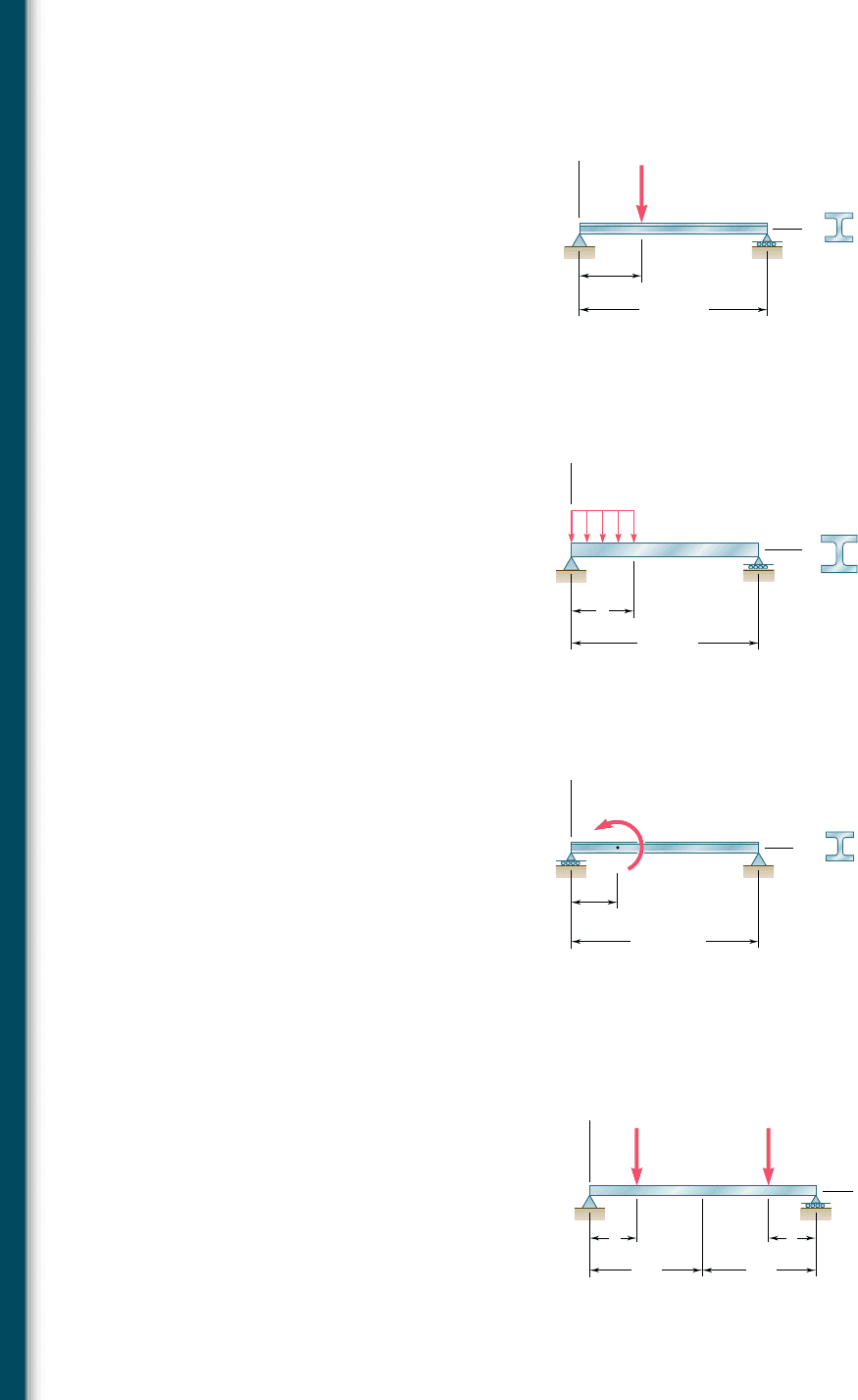
9.13 For the beam and loading shown, determine the deflection at point

C. Use E 5 29 3 10

psi.

L  15 ft

W14  30

a  5 ft

P  35 kips

Fig. P9.13

9.14 For the beam and loading shown, knowing that a 5 2 m, w 5

50 kN/m, and E 5 200 GPa, determine (a) the slope at support A,

(b) the deflection at point C.

Fig. P9.14

L  6 m

W310  38.7

9.15 For the beam and loading shown, determine the deflection at point

C. Use E 5 200 GPa.

Fig. P9.15

L  4.8 m

W200  35.9

a  1.2 m

 60 kN · m

9.16 Knowing that beam AE is an S200 3 27.4 rolled shape and that

P 5 17.5 kN, L 5 2.5 m, a 5 0.8 m and E 5 200 GPa, determine

(a) the equation of the elastic curve for portion BD, (b) the deflec-

tion at the center C of the beam.

Fig. P9.16

BC D

L/2L/2

bee80288_ch09_548-629.indd Page 568 11/18/10 8:56:40 PM user-f499bee80288_ch09_548-629.indd Page 568 11/18/10 8:56:40 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

569

Problems

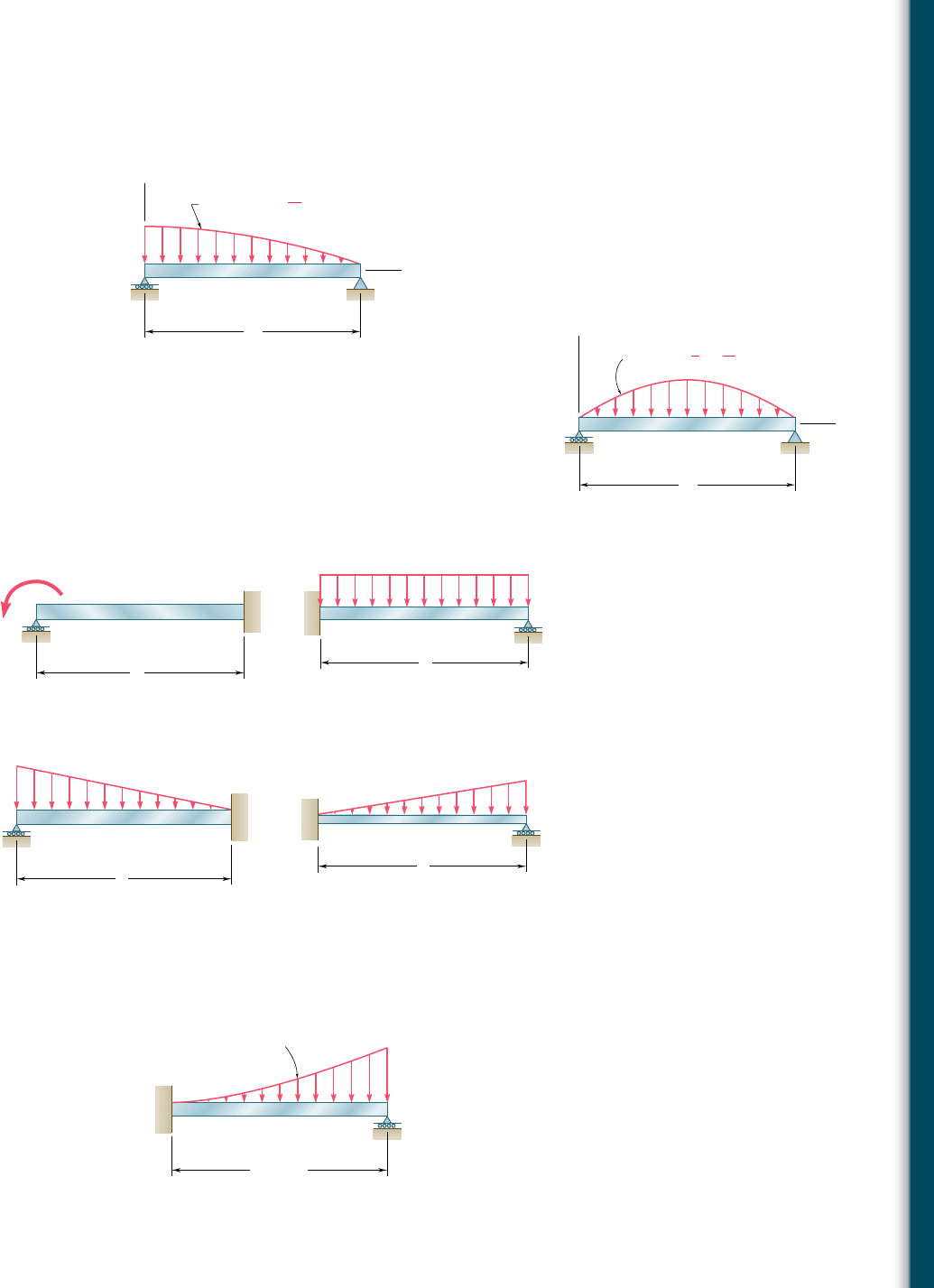
9.17 For the beam and loading shown, determine (a) the equation of

the elastic curve, (b) the slope at end A, (c) the deflection at the

midpoint of the span.

Fig. P9.17

w  w

[]



9.18 For the beam and loading shown, determine (a) the equation of

the elastic curve, (b) the slope at end A, (c) the deflection at the

midpoint of the span.

9.19 through 9.22 For the beam and loading shown, determine the

reaction at the roller support.

Fig. P9.18

w  4w

0[]



Fig. P9.19

Fig. P9.20

Fig. P9.22

Fig. P9.21

9.23 For the beam shown, determine the reaction at the roller support

when w

5 15 kN/m.

Fig. P9.23

L  3 m

w  w

(x/L)

bee80288_ch09_548-629.indd Page 569 10/30/10 11:19:25 PM user-f499bee80288_ch09_548-629.indd Page 569 10/30/10 11:19:25 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

570

Deﬂ ection of Beams

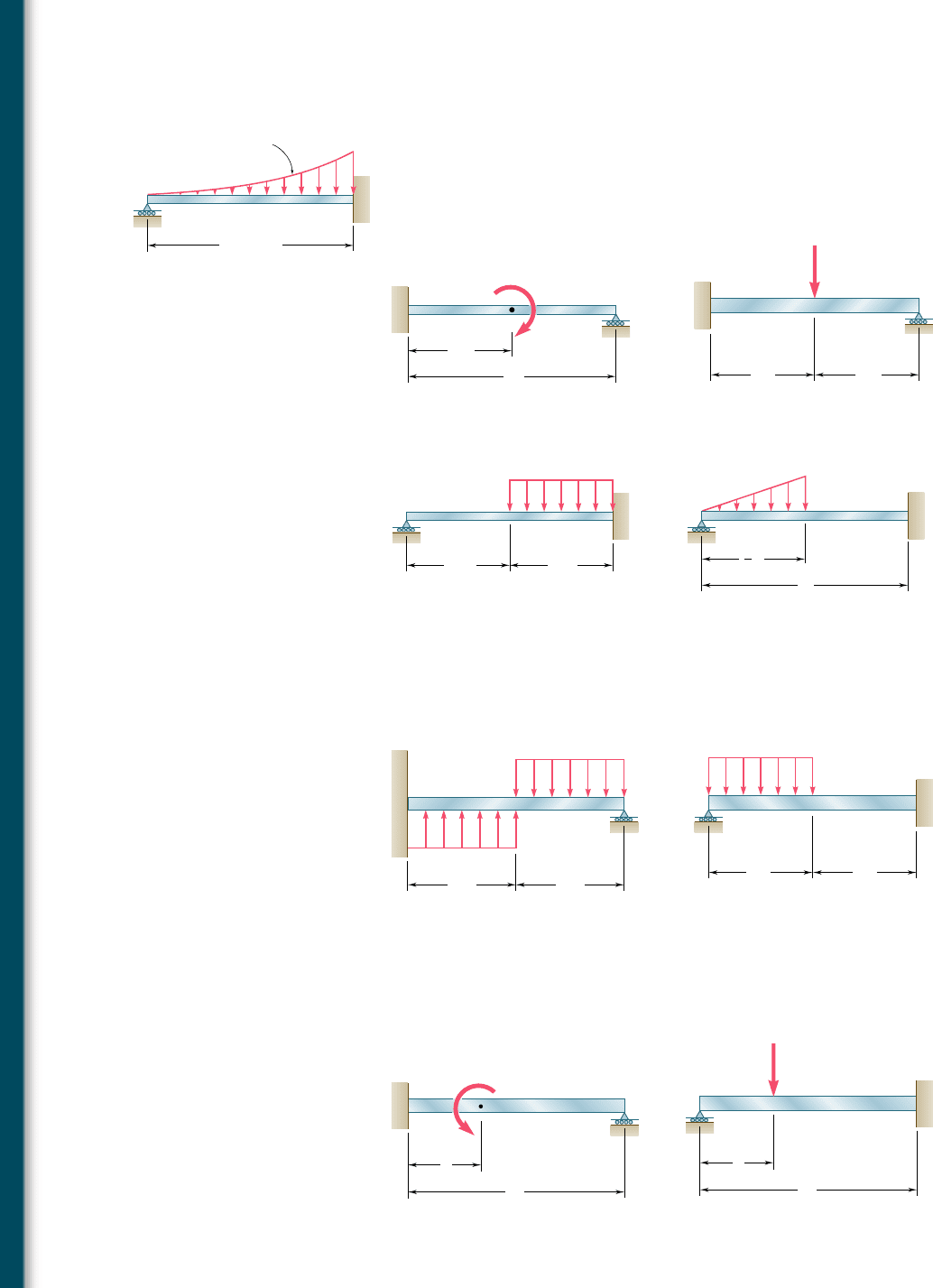
9.24 For the beam shown, determine the reaction at the roller support

when w

5 6 kips/ft.

9.25 through 9.28 Determine the reaction at the roller support

and draw the bending moment diagram for the beam and loading

shown.

L  12 ft

w  w

(x/L)

Fig. P9.24

Fig. P9.25

L/2

Fig. P9.26

L/2 L/2

Fig. P9.27

L/2 L/2

Fig. P9.28

9.29 and 9.30 Determine the reaction at the roller support and the

deflection at point C.

L/2 L/2

Fig. P9.29

L/2 L/2

Fig. P9.30

9.31 and 9.32 Determine the reaction at the roller support and the

deflection at point D if a is equal to Ly3.

Fig. P9.31 Fig. P9.32

bee80288_ch09_548-629.indd Page 570 10/30/10 11:19:40 PM user-f499bee80288_ch09_548-629.indd Page 570 10/30/10 11:19:40 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

9.33 and 9.34 Determine the reaction at A and draw the bending

moment diagram for the beam and loading shown.

571

Fig. P9.33

L/2 L/2

Fig. P9.34

Photo 9.2 In this roof structure, each of the joists applies a concentrated load to the

beam that supports it.

9.6 Using Singularity Functions to Determine

the Slope and Deﬂ ection of a Beam

*9.6 USING SINGULARITY FUNCTIONS TO DETERMINE

THE SLOPE AND DEFLECTION OF A BEAM

Reviewing the work done so far in this chapter, we note that the inte-

gration method provides a convenient and effective way of determining

the slope and deflection at any point of a prismatic beam, as long as

the bending moment can be represented by a single analytical function

M(x). However, when the loading of the beam is such that two different

functions are needed to represent the bending moment over the entire

length of the beam, as in Example 9.03 (Fig. 9.16), four constants of

integration are required, and an equal number of equations, expressing

continuity conditions at point D, as well as boundary conditions at the

supports A and B, must be used to determine these constants. If three

or more functions were needed to represent the bending moment,

additional constants and a corresponding number of additional equa-

tions would be required, resulting in rather lengthy computations. Such

would be the case for the beam shown in Photo 9.2. In this section

these computations will be simplified through the use of the singularity

functions discussed in Sec. 5.5.

bee80288_ch09_548-629.indd Page 571 10/30/10 11:20:00 PM user-f499bee80288_ch09_548-629.indd Page 571 10/30/10 11:20:00 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

572

Deﬂ ection of Beams

Let us consider again the beam and loading of Example 9.03

(Fig. 9.16) and draw the free-body diagram of that beam (Fig. 9.27).

Using the appropriate singularity function, as explained in Sec. 5.5,

to represent the contribution to the shear of the concentrated load

P, we write

V1x25

2 PHx 2

Integrating in x and recalling from Sec. 5.5 that in the absence of

any concentrated couple, the expression obtained for the bending

moment will not contain any constant term, we have

M1x25

x 2 PHx 2

(9.44)

Substituting for M(x) from (9.44) into Eq. (9.4), we write



x 2 PHx 2

(9.45)

and, integrating in x,

EI u 5 EI

PHx 2

1 C

(9.46)

EI y 5

PHx 2

1 C

x 1 C

(9.47)†

The constants C

and C

can be determined from the boundary

con ditions shown in Fig. 9.28. Letting x 5 0, y 5 0 in Eq. (9.47),

we have

0 5 0 2

PH0 2

1 0 1 C

which reduces to C

5 0, since any bracket containing a negative

quantity is equal to zero. Letting now x 5 L, y 5 0, and C

5 0 in

Eq. (9.47), we write

0 5

1 C

Since the quantity between brackets is positive, the brackets can be

replaced by ordinary parentheses. Solving for C

, we have

7PL

128

We check that the expressions obtained for the constants C

and C

are the same that were found earlier in Sec. 9.3. But the

need for additional constants C

and C

has now been eliminated,

and we do not have to write equations expressing that the slope and

the deflection are continuous at point D.

3L/4

L/4

Fig. 9.16 (repeated)

†The continuity conditions for the slope and deflection at D are “built-in” in Eqs. (9.46)

and (9.47). Indeed, the difference between the expressions for the slope u

in AD and the

slope u

in DB is represented by the term 2

x 2

in Eq. (9.46), and this term is

equal to zero at D. Similarly, the difference between the expressions for the deflection y

in AD and the deflection y

in DB is represented by the term 2

x 2

in Eq. (9.47),

and this term is also equal to zero at D.

x  0, y  0

[]

x  L, y  0

[]

Fig. 9.28 Boundary conditions for

beam of Fig. 9.16.

L/4

3L/4

Fig. 9.27 Free-body diagram for

beam of Fig. 9.16.

bee80288_ch09_548-629.indd Page 572 10/30/10 11:20:08 PM user-f499bee80288_ch09_548-629.indd Page 572 10/30/10 11:20:08 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

573

EXAMPLE 9.06

For the beam and loading shown (Fig. 9.29a) and using singularity func-

tions, (a) express the slope and deflection as functions of the distance x

from the support at A, (b) determine the deflection at the midpoint D. Use

E 5 200 GPa and I 5 6.87 3 10

(a) We note that the beam is loaded and supported in the same

manner as the beam of Example 5.05. Referring to that example, we recall

that the given distributed loading was replaced by the two equivalent

open-ended loadings shown in Fig. 9.29b and that the following expres-

sions were obtained for the shear and bending moment:

V1x2521.5

x 2 0.6

1 1.5

x 2 1.8

1 2.6 2 1.2

x 2 0.6

M1x2520.75

x 2 0.6

1 0.75

x 2 1.8

1 2.6x 2 1.2

x 2 0.6

2 1.44

x 2 2.6

Integrating the last expression twice, we obtain

EIu 520.25

x 2 0.6

1 0.25

x 2 1.8

1 1.3x

2 0.6

x 2 0.6

2 1.44

x 2 2.6

1 C

(9.48)

EIy 520.0625

x 2 0.6

1 0.0625

x 2 1.8

1 0.4333x

2 0.2

x 2 0.6

2 0.72

x 2 2.6

1 C

x 1 C

(9.49)

The constants C

and C

can be determined from the boundary

conditions shown in Fig. 9.30. Letting x 5 0, y 5 0 in Eq. (9.49) and

noting that all the brackets contain negative quantities and, therefore, are

equal to zero, we conclude that C

5 0. Letting now x 5 3.6, y 5 0, and

5 0 in Eq. (9.49), we write

0 520.0625

3.0

1 0.0625

1.8

1 0.433313.62

2 0.2

3.0

2 0.72

1.0

1 C

13.621 0

Since all the quantities between brackets are positive, the brackets can be

replaced by ordinary parentheses. Solving for C

, we find C

5 22.692.

 1.5 kN/m

P  1.2 kN

 2.6 kN

 w

  1.5 kN/m

 1.44 kN · m

xAE

(a)

(b)

0.6 m

1.2 m

3.6 m

0.8 m 1.0 m

0.6 m

2.6 m

1.8 m

Fig. 9.29

[x  0, y  0] [x  3.6, y  0]

Fig. 9.30

(b) Substituting for C

and C

into Eq. (9.49) and making x 5 x

1.8 m, we find that the deflection at point D is defined by the relation

EIy

520.0625

1.2

1 0.0625

1 0.433311.82

2 0.2

1.2

2 0.72

20.8

2 2.69211.82

The last bracket contains a negative quantity and, therefore, is equal to

zero. All the other brackets contain positive quantities and can be replaced

by ordinary parentheses. We have

EIy

520.062511.22

1 0.0625102

1 0.4333

1.8

2 0.2

1.2

2 0 2 2.692

1.8

522.794

Recalling the given numerical values of E and I, we write

1200 GPa216.87 3 10

522.794 kN ? m

5213.64 3 10

m 522.03 mm

bee80288_ch09_548-629.indd Page 573 11/18/10 8:56:49 PM user-f499bee80288_ch09_548-629.indd Page 573 11/18/10 8:56:49 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

574

SAMPLE PROBLEM 9.4

For the prismatic beam and loading shown, determine (a) the equation of

the elastic curve, (b) the slope at A, (c) the maximum deflection.

SOLUTION

Bending Moment. The equation defining the bending moment of the

beam was obtained in Sample Prob. 5.9. Using the modified loading diagram

shown, we had [Eq. (3)]:

M1x252

Hx 2

a. Equation of the Elastic Curve. Using Eq. (9.4), we write

Hx 2

(1)

and, integrating twice in x,

EI u 52

12L

Hx 2

1 C

(2)

EI y 52

60L

30L

Hx 2

1 C

x 1 C

(3)

Boundary Conditions.

[x 5 0, y 5 0]: Using Eq. (3) and noting that each bracket H I con-

tains a negative quantity and, thus, is equal to zero, we find C

5 0.

[x 5 L, y 5 0]: Again using Eq. (3), we write

0 52

30L

1 C

Substituting C

and C

into Eqs. (2) and (3), we have

EI u 52

12L

Hx 2

192

(4)

EI y 52

60L

30L

Hx 2

192

x

(5) b

b. Slope at A. Substituting x 5 0 into Eq. (4), we find

EI u

c b

c. Maximum Deflection. Because of the symmetry of the supports and

loading, the maximum deflection occurs at point C, where

L. Substitut-

ing into Eq. (5), we obtain

EI y

max

5 w

1 0 1

192

d52

120

max

120EI

w b

L/2 L/2

 



L/2 L/2

 

[ x  0, y  0 ][ x  L, y  0 ]

L/2

max



bee80288_ch09_548-629.indd Page 574 11/19/10 3:17:10 PM user-f499bee80288_ch09_548-629.indd Page 574 11/19/10 3:17:10 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

575

SAMPLE PROBLEM 9.5

The rigid bar DEF is welded at point D to the uniform steel

beam AB. For the loading shown, determine (a) the equation

of the elastic curve of the beam, (b) the deflection at the mid-

point C of the beam. Use E 5 29 3 10

psi.

SOLUTION

Bending Moment. The equation defining the bending moment of the

beam was obtained in Sample Prob. 5.10. Using the modified loading dia-

gram shown and expressing x in feet, we had [Eq. (3)]:

M(x) 5 225x

1 480x 2 160 Hx 2 11I

2 480Hx 2 11I

lb ? ft

a. Equation of the Elastic Curve. Using Eq. (8.4), we write

EI(d

yydx

) 5 225x

1 480x 2 160Hx 2 11I

2 480Hx 2 11I

lb ? ft (1)

and, integrating twice in x,

EI u 5 28.333x

1 240x

2 80Hx 2 11I

2 480Hx 2 11I

1 C

lb ? ft

(2)

EI y 5 22.083x

1 80x

2 26.67Hx 2 11I

2 240Hx 2 11I

1 C

x 1 C

lb ? ft

(3)

Boundary Conditions.

[x 5 0, y 5 0]: Using Eq. (3) and noting that each bracket H I con-

tains a negative quantity and, thus, is equal to zero, we find C

5 0.

[x 5 16 ft, y 5 0]: Again using Eq. (3) and noting that each bracket con-

tains a positive quantity and, thus, can be replaced by a parenthesis, we write

0 522.083

1 80

2 26.67

2 240

1 C

5211.36 3 10

Substituting the values found for C

and C

into Eq. (3), we have

EI y 522.083x

1 80x

2 26.67

x 2 11

2 240

x 2 11

2 11.36 3 10

xl

? ft

(39) b

To determine EI, we recall that E 5 29 3 10

psi and compute

I 5

1 in.

3 in.

5 2.25 in

EI 5 129 3 10

psi212.25 in

25 65.25 3 10

lb ? in

However, since all previous computations have been carried out with feet

as the unit of length, we write

EI 5

65.25 3 10

lb ? in

1 ft/12 in.

5 453.1 3 10

lb ? ft

b. Deflection at Midpoint C. Making x 5 8 ft in Eq. (39), we write

EI y

522.083182

1 80182

2 26.67

2 240

2 11.36 3 10

182

Noting that each bracket is equal to zero and substituting for EI its numeri-

cal value, we have

(453.1 3 10

lb ? ft

5 258.45 3 10

lb ? ft

and, solving for y

: y

5 20.1290 ft y

5 21.548 in. b

Note that the deflection obtained is not the maximum deflection.

F E

50 lb/ft

160 lb

8 ft

3 ft

3 in.

1 in.

5 ft

 50 lb/ft

 480 lb · ft

 480 lb R

 160 lb

5 ft11 ft

16 ft

[ x  0, y  0 ]

[ x  16 ft, y  0 ]

8 ft 8 ft

bee80288_ch09_548-629.indd Page 575 11/19/10 3:17:29 PM user-f499bee80288_ch09_548-629.indd Page 575 11/19/10 3:17:29 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

576

SAMPLE PROBLEM 9.6

For the uniform beam ABC, (a) express the reaction at A in terms of P, L,

a, E, and I, (b) determine the reaction at A and the deflection under the

load when a 5 Ly2.

SOLUTION

Reactions. For the given vertical load P the reactions are as shown.

We note that they are statically indeterminate.

Shear and Bending Moment. Using a step function to represent the

contribution of P to the shear, we write

V1x25 R

2 P

x 2 a

Integrating in x, we obtain the bending moment:

M1x25 R

x 2 P

x 2 a

Equation of the Elastic Curve. Using Eq. (9.4), we write



5 R

x 2 PHx 2 aI

Integrating twice in x,

5 EI u 5

PHx 2 aI

1 C

EI y 5

PHx 2 aI

1 C

x 1 C

Boundary Conditions. Noting that the bracket

x 2 a

is equal to

zero for x 5 0, and to (L 2 a) for x 5 L, we write

x 5 0, y 5 0

(1)

x 5 L, u 5 0

L 2 a

1 C

5 0 (2)

x 5 L, y 5 0

L 2 a

1 C

L 1 C

5 0 (3)

a. Reaction at A. Multiplying Eq. (2) by L, subtracting Eq. (3) member

by member from the equation obtained, and noting that C

5 0, we have

P1L 2 a2

33L 2 1L 2 a245 0

5 P

1 2

1 1

x b

We note that the reaction is independent of E and I.

b. Reaction at A and Deflection at B when a 5

L. Making

in the expression obtained for R

, we have

5 P

1 2

1 1

5 5P

16 R

Px b

Substituting a 5 Ly2 and R

5 5Py16 into Eq. (2) and solving for C

, we

find C

5 2PL

y32. Making x 5 Ly2, C

5 2PL

y32, and C

5 0 in the

expression obtained for y, we have

7PL

768EI

7PL

768EI

w b

Note that the deflection obtained is not the maximum deflection.

[ x  0, y  0 ]

[ x  L,  0 ]



L/2L/2

bee80288_ch09_548-629.indd Page 576 10/30/10 11:20:39 PM user-f499bee80288_ch09_548-629.indd Page 576 10/30/10 11:20:39 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09