Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

PROBLEMS

577

Use singularity functions to solve the following problems

and assume that the flexural rigidity EI of each beam is

constant.

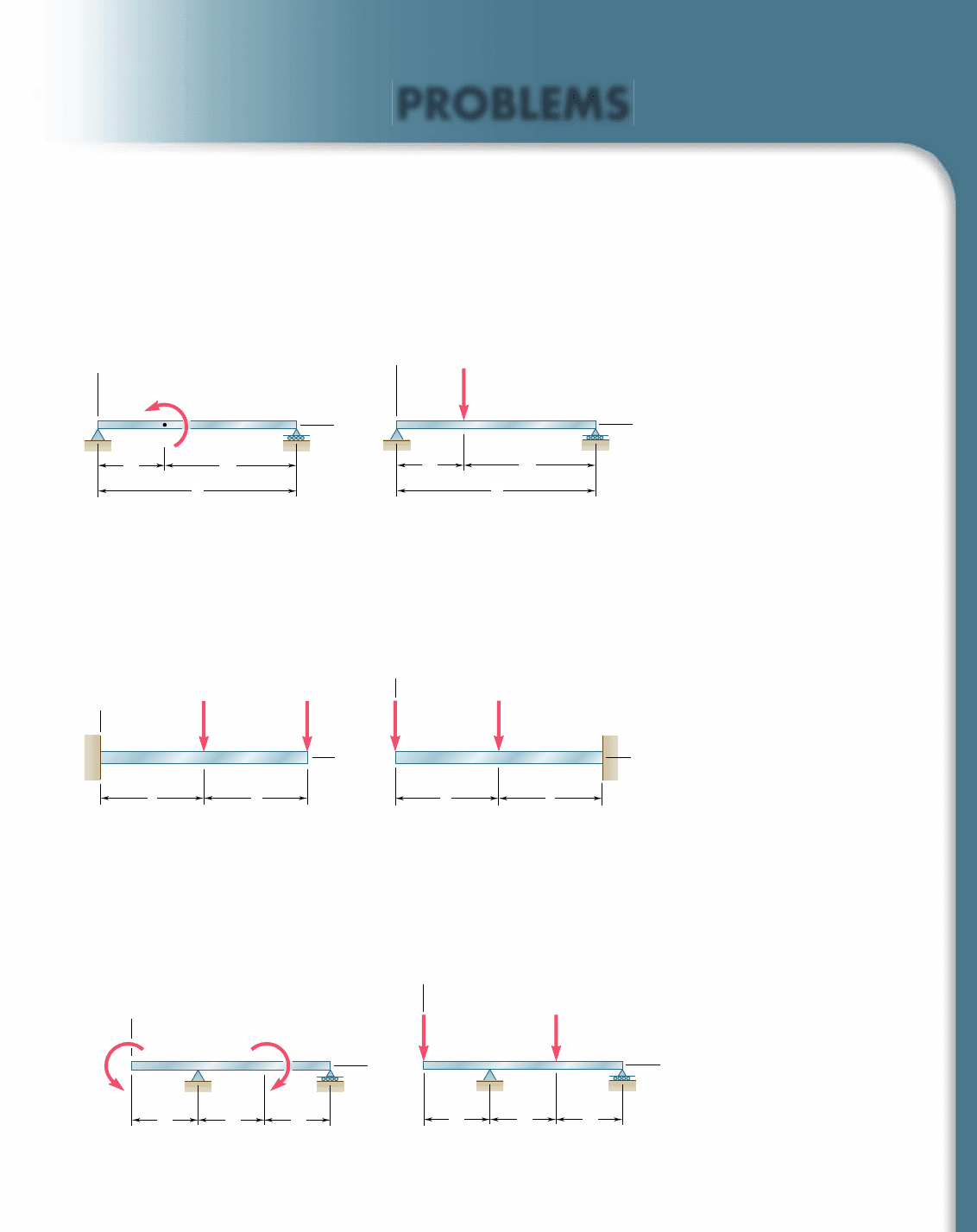
9.35 and 9.36 For the beam and loading shown, determine (a) the

equation of the elastic curve, (b) the slope at end A, (c) the deflec-

tion of point C.

Fig. P9.35

Fig. P9.36

9.37 and 9.38 For the beam and loading shown, determine (a) the

equation of the elastic curve, (b) the slope at the free end, (c) the

deflection of the free end.

P P

Fig. P9.37

Fig. P9.38

9.39 and 9.40 For the beam and loading shown, determine (a) the

deflection at end A, (b) the deflection at point C, (c) the slope at

end D.

Fig. P9.39

aaa

P P

Fig. P9.40

bee80288_ch09_548-629.indd Page 577 10/30/10 11:20:50 PM user-f499bee80288_ch09_548-629.indd Page 577 10/30/10 11:20:50 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

578

Deﬂ ection of Beams

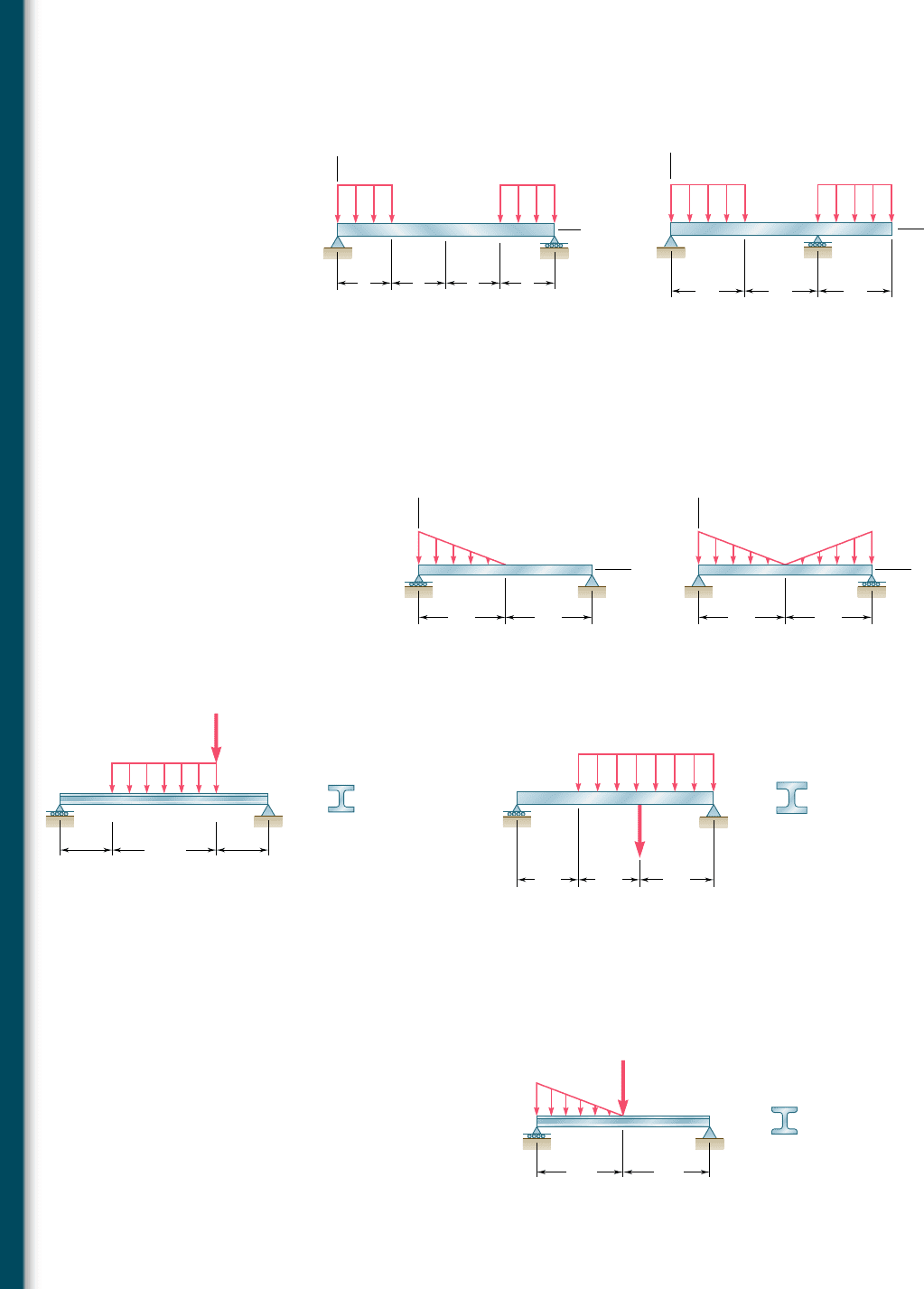
9.41 For the beam and loading shown, determine (a) the equation of

the elastic curve, (b) the deflection at the midpoint C.

aaa

w w

Fig. P9.41

L/2 L/2

L/2

w w

Fig. P9.42

9.42 For the beam and loading shown, determine (a) the equation of

the elastic curve, (b) the deflection at point B, (c) the deflection

at point D.

9.43 and 9.44 For the beam and loading shown, determine (a) the

equation of the elastic curve, (b) the deflection at the midpoint C.

L/2 L/2

Fig. P9.43

L/2 L/2

Fig. P9.44

9.45 For the beam and loading shown, determine (a) the slope at end

A, (b) the deflection at point C. Use E 5 200 GPa.

12 kN/m

0.4 m 0.4 m

0.8 m

W150  13.5

20 kN

Fig. P9.45

9.46 For the beam and loading shown, determine (a) the slope at end A,

(b) the deflection at point C. Use E 5 29 3 10

psi.

9.47 For the beam and loading shown, determine (a) the slope at end

A, (b) the deflection at the midpoint C. Use E 5 200 GPa.

W16  57

5 ft

5 ft 6 ft

3 kips/ft

20 kips

Fig. P9.46

S130  15

1 m 1 m

8 kN

48 kN/m

Fig. P9.47

bee80288_ch09_548-629.indd Page 578 11/1/10 8:39:08 PM user-f499bee80288_ch09_548-629.indd Page 578 11/1/10 8:39:08 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

579

Problems

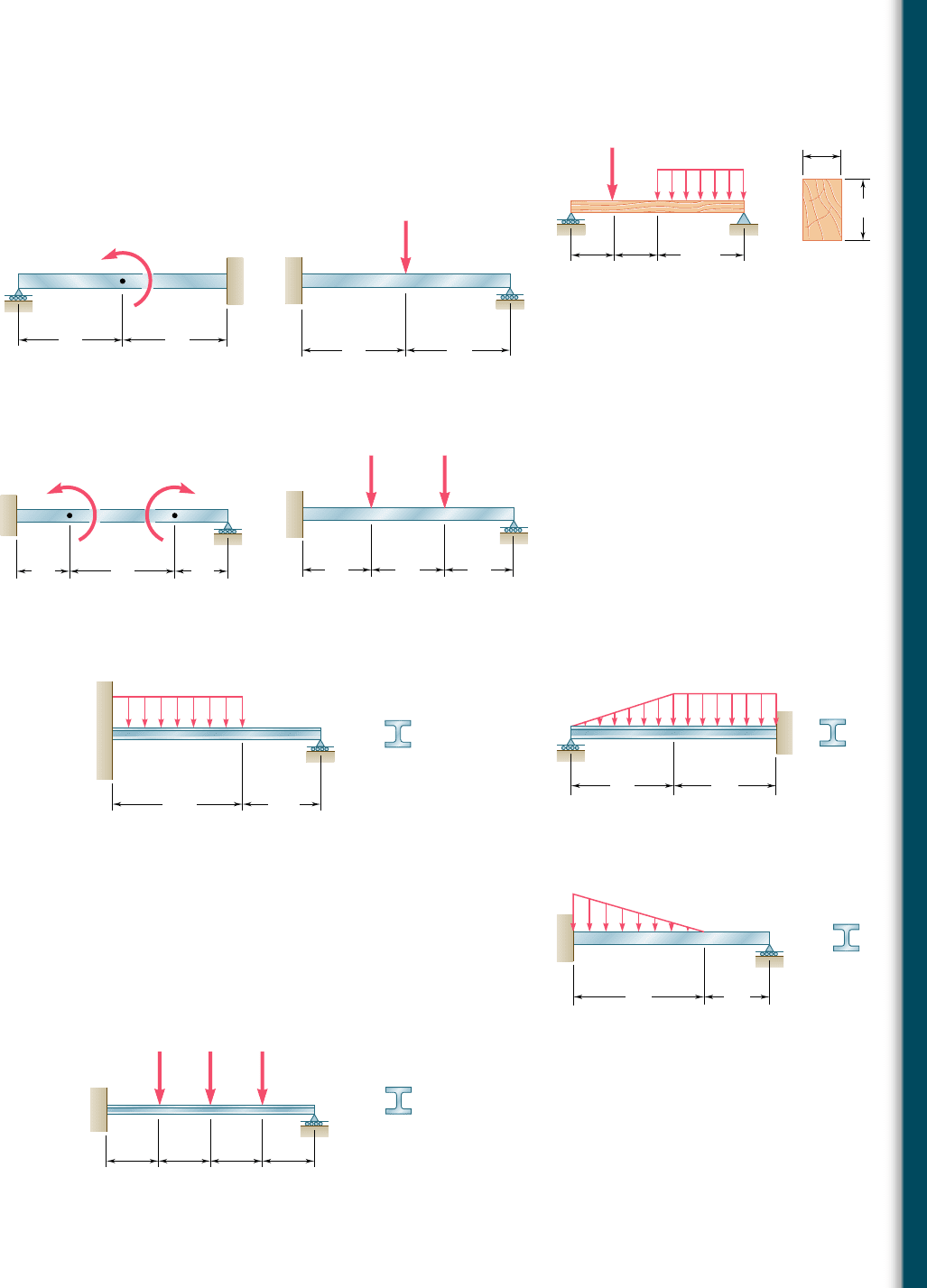
9.48 For the timber beam and loading shown, determine (a) the

slope at end A, (b) the deflection at the midpoint C. Use E 5

1.6 3 10

psi.

9.49 and 9.50 For the beam and loading shown, determine (a) the

reaction at the roller support, (b) the deflection at point C.

350 lb/ft

2 kips

1.75 ft 1.75 ft

3.5 ft

3.5 in.

5.5 in.

Fig. P9.48

L/2 L/2

Fig. P9.49

L/2 L/2

Fig. P9.50

9.51 and 9.52 For the beam and loading shown, determine (a) the

reaction at the roller support, (b) the deflection at point B.

L/4 L/2 L/4

Fig. P9.51

L/3

A B C

L/3 L/3

P P

Fig. P9.52

9.53 For the beam and loading shown, determine (a) the reaction at

point C, (b) the deflection at point B. Use E 5 200 GPa.

14 kN/m

W410  60

5 m 3 m

Fig. P9.53

9.54 For the beam and loading shown, determine (a) the reaction at

point A, (b) the deflection at point C. Use E 5 29 3 10

psi.

9.55 For the beam and loading shown, determine (a) the reaction at

point C, (b) the deflection at point B. Use E 5 29 3 10

psi.

9.56 For the beam shown and knowing that P 5 40 kN, determine

(a) the reaction at point E, (b) the deflection at point C. Use E 5

200 GPa.

2.5 kips/ft

6 ft 6 ft

W10  22

Fig. P9.54

W12  40

8 ft

4 ft

 9 kips/ft

Fig. P9.55

0.5 m 0.5 m 0.5 m 0.5 m

B CD

W200  46.1

P P

Fig. P9.56

bee80288_ch09_548-629.indd Page 579 10/30/10 11:21:18 PM user-f499bee80288_ch09_548-629.indd Page 579 10/30/10 11:21:18 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

9.7 METHOD OF SUPERPOSITION

When a beam is subjected to several concentrated or distributed

loads, it is often found convenient to compute separately the slope

and deflection caused by each of the given loads. The slope and

deflection due to the combined loads are then obtained by applying

the principle of superposition (Sec. 2.12) and adding the values of

the slope or deflection corresponding to the various loads.

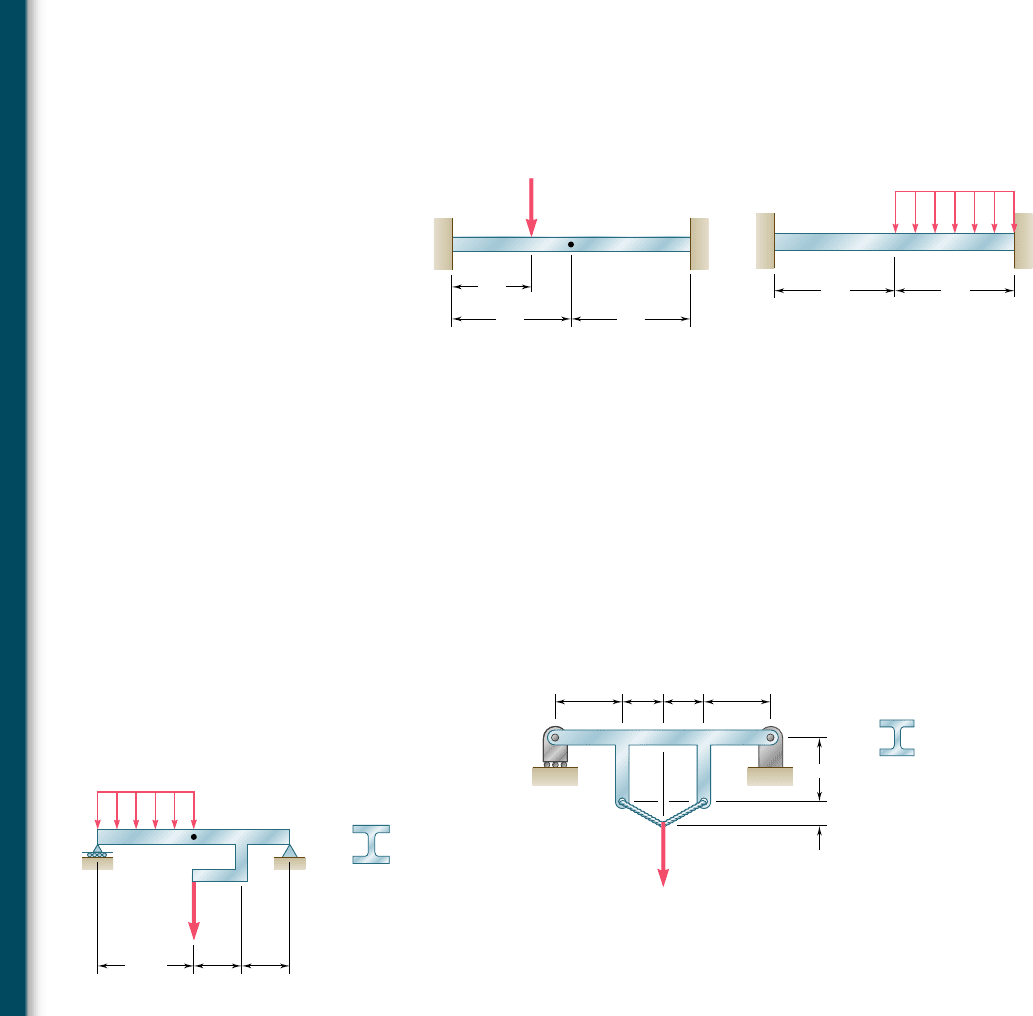
9.57 and 9.58 For the beam and loading shown, determine (a) the

reaction at point A, (b) the deflection at midpoint C.

L/2 L/2

A B CD

L/3

Fig. P9.57

L/2 L/2

Fig. P9.58

9.59 through 9.62 For the beam and loading indicated, determine

the magnitude and location of the largest downward deflection.

9.59 Beam and loading of Prob. 9.45.

9.60 Beam and loading of Prob. 9.46.

9.61 Beam and loading of Prob. 9.47.

9.62 Beam and loading of Prob. 9.48.

9.63 The rigid bars BF and DH are welded to the rolled-steel beam AE

as shown. Determine for the loading shown (a) the deflection at

point B, (b) the deflection at midpoint C of the beam. Use E 5

200 GPa.

0.4 m

W100  19.3

0.15 m

0.5 m 0.3 m 0.3 m 0.5 m

100 kN

Fig. P9.63

9.64 The rigid bar DEF is welded at point D to the rolled-steel beam

AB. For the loading shown, determine (a) the slope at point A,

(b) the deflection at midpoint C of the beam. Use E 5 200 GPa.

1.2 m

50 kN

30 kN/m

1.2 m

2.4 m

A B

W460  52

Fig. P9.64

580

Deﬂ ection of Beams

bee80288_ch09_548-629.indd Page 580 10/30/10 11:21:39 PM user-f499bee80288_ch09_548-629.indd Page 580 10/30/10 11:21:39 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

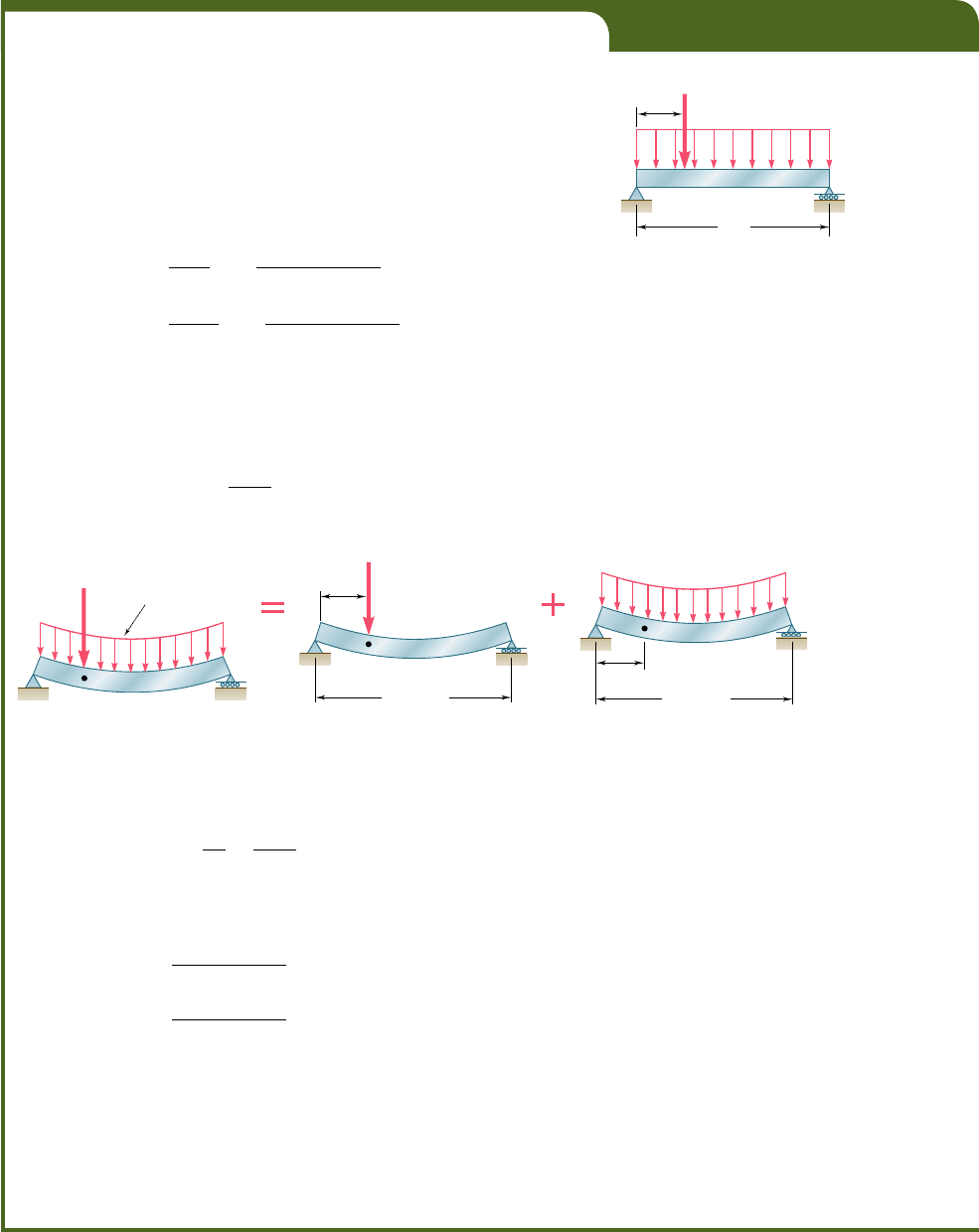
EXAMPLE 9.07

Determine the slope and deflection at D for the beam and loading

shown (Fig. 9.31), knowing that the flexural rigidity of the beam is

EI 5 100 MN ? m

The slope and deflection at any point of the beam can be obtained

by superposing the slopes and deflections caused respectively by the con-

centrated load and by the distributed load (Fig. 9.32).

Since the concentrated load in Fig. 9.32b is applied at quarter span,

we can use the results obtained for the beam and loading of Example 9.03

and write

32EI

1150 3 10

2182

100 3 10

523 3 10

rad

3PL

256EI

31150 3 10

2182

256

100 3 10

529 3 10

529 mm

On the other hand, recalling the equation of the elastic curve obtained

for a uniformly distributed load in Example 9.02, we express the deflec-

tion in Fig. 9.32c as

24E

12x

1 2L x

2 L

x2 (9.50)

150 kN

20 kN/m

2 m

8 m

Fig. 9.31

x  2 m

L  8 m

(c)

w  20 kN/m

Fig. 9.32

20 kN/m

150 kN

(a)

2 m

L  8 m

P  150 kN

(b)

and, differentiating with respect to x,

u 5

24EI

124x

1 6L x

2 L

2 (9.51)

Making w 5 20 kN/m, x 5 2 m, and L 5 8 m in Eqs. (9.51) and (9.50),

we obtain

20 3 10

241100 3 10

123522 522.93 3 10

rad

20 3 10

241100 3 10

129122 527.60 3 10

60 mm

Combining the slopes and deflections produced by the concentrated and

the distributed loads, we have

5 1u

1 1u

523 3 10

2 2.93 3 10

525

93 3 10

5 1y

1 1y

529 mm 2 7.60 mm 5216.60 mm

581

bee80288_ch09_548-629.indd Page 581 10/30/10 11:21:48 PM user-f499bee80288_ch09_548-629.indd Page 581 10/30/10 11:21:48 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

582

Deﬂ ection of Beams

To facilitate the task of practicing engineers, most structural

and mechanical engineering handbooks include tables giving the

deflections and slopes of beams for various loadings and types of

support. Such a table will be found in Appendix D. We note that the

slope and deflection of the beam of Fig. 9.31 could have been deter-

mined from that table. Indeed, using the information given under

cases 5 and 6, we could have expressed the deflection of the beam

for any value x # Ly4. Taking the derivative of the expression

obtained in this way would have yielded the slope of the beam over

the same interval. We also note that the slope at both ends of the

beam can be obtained by simply adding the corresponding values

given in the table. However, the maximum deflection of the beam

of Fig. 9.31 cannot be obtained by adding the maximum deflections

of cases 5 and 6, since these deflections occur at different points of

the beam.†

9.8 APPLICATION OF SUPERPOSITION TO STATICALLY

INDETERMINATE BEAMS

We often find it convenient to use the method of superposition to

determine the reactions at the supports of a statically indeterminate

beam. Considering first the case of a beam indeterminate to the first

degree (cf. Sec. 9.5), such as the beam shown in Photo 9.3, we follow

the approach described in Sec. 2.9. We designate one of the reac-

tions as redundant and eliminate or modify accordingly the corre-

sponding support. The redundant reaction is then treated as an

unknown load that, together with the other loads, must produce

deformations that are compatible with the original supports. The

slope or deflection at the point where the support has been modified

or eliminated is obtained by computing separately the deformations

caused by the given loads and by the redundant reaction, and by

superposing the results obtained. Once the reactions at the supports

have been found, the slope and deflection can be determined in the

usual way at any other point of the beam.

†An approximate value of the maximum deflection of the beam can be obtained by plot-

ting the values of y corresponding to various values of x. The determination of the exact

location and magnitude of the maximum deflection would require setting equal to zero

the expression obtained for the slope of the beam and solving this equation for x.

Photo 9.3 The continuous beams supporting

this highway overpass have three supports and

are thus statically indeterminate.

bee80288_ch09_548-629.indd Page 582 10/30/10 11:21:54 PM user-f499bee80288_ch09_548-629.indd Page 582 10/30/10 11:21:54 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

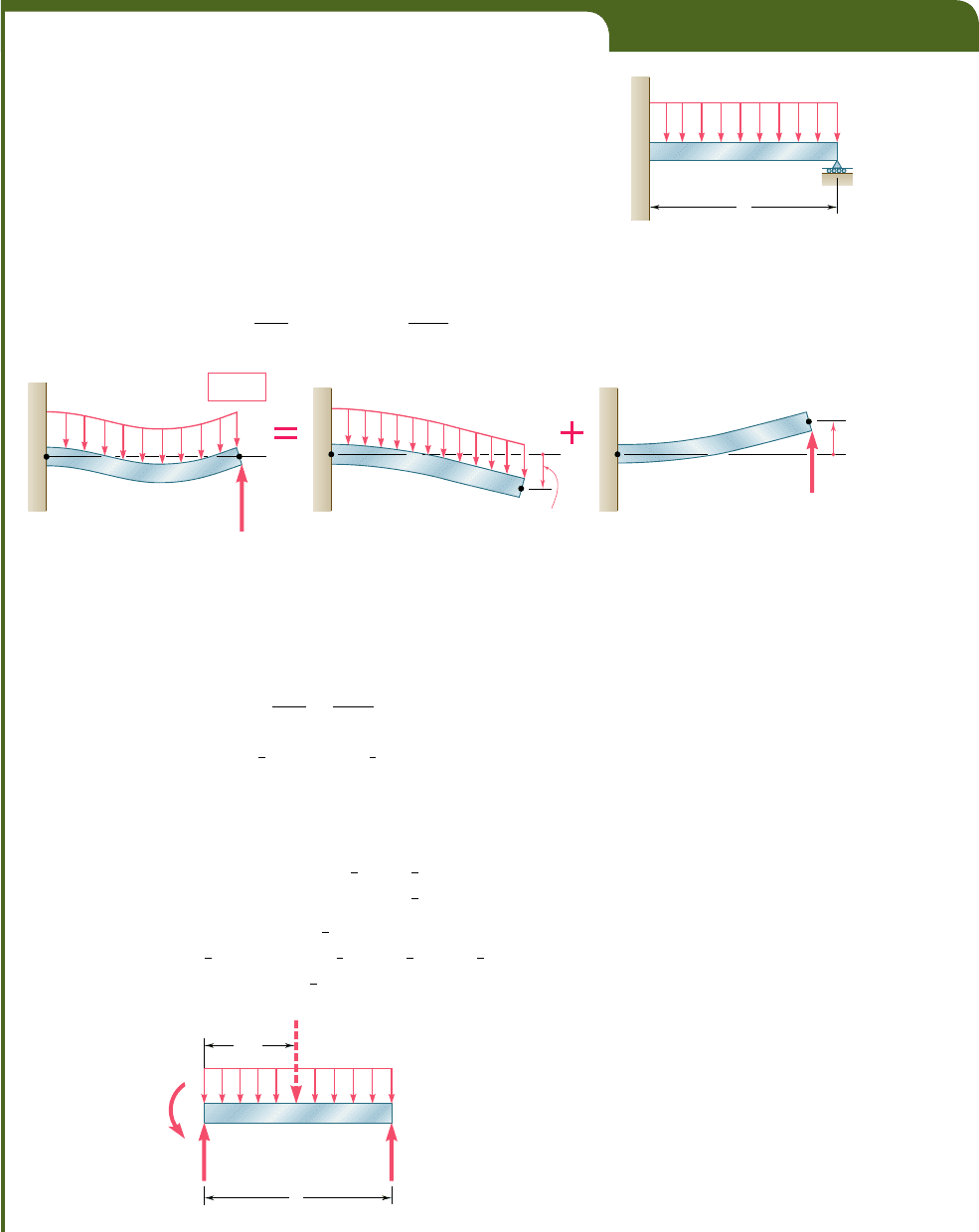
EXAMPLE 9.08

Determine the reactions at the supports for the prismatic beam and loading

shown in Fig. 9.33. (This is the same beam and loading as in Example 9.05

of Sec. 9.5.)

We consider the reaction at B as redundant and release the beam

from the support. The reaction R

is now considered as an unknown load

(Fig. 9.34a) and will be determined from the condition that the deflection

of the beam at B must be zero. The solution is carried out by considering

separately the deflection (y

)

caused at B by the uniformly distributed

load w (Fig. 9.34b) and the deflection (y

)

produced at the same point

by the redundant reaction R

(Fig. 9.34c).

From the table of Appendix D (cases 2 and 1), we find that

8EI

1y

3EI

Writing that the deflection at B is the sum of these two quantities and

that it must be zero, we have

5 1y

1 1y

5 0

8EI

3EI

5 0

and, solving for R

, R

wLR

wLx

Drawing the free-body diagram of the beam (Fig. 9.35) and writing

the corresponding equilibrium equations, we have

1xgF

5 0: R

1 R

2 wL 5

(9.52)

5 wL 2 R

5 wL 2

wL 5

5 0: M

1 R

L 2

5 0 (9.53)

2 R

L 5

Fig. 9.33

)

 0

)

(a)(b)(c)

Fig. 9.34

L/2

Fig. 9.35

583

bee80288_ch09_548-629.indd Page 583 11/18/10 8:57:04 PM user-f499bee80288_ch09_548-629.indd Page 583 11/18/10 8:57:04 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

The beam considered in the preceding example was indetermi-

nate to the first degree. In the case of a beam indeterminate to the

second degree (cf. Sec. 9.5), two reactions must be designated as

redundant, and the corresponding supports must be eliminated or

modified accordingly. The redundant reactions are then treated as

unknown loads which, simultaneously and together with the other

loads, must produce deformations which are compatible with the

original supports. (See Sample Prob. 9.9.)

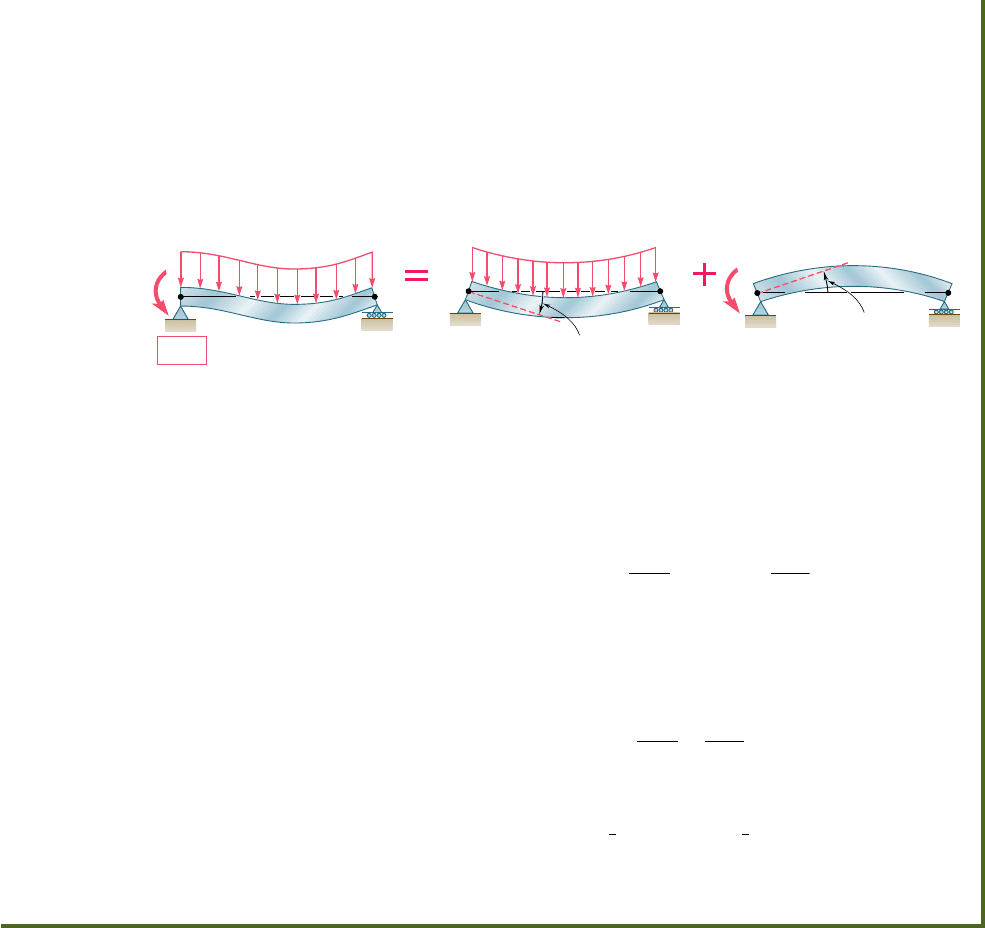
Alternative Solution. We may consider the couple exerted at the

fixed end A as redundant and replace the fixed end by a pin-and-bracket

support. The couple M

is now considered as an unknown load (Fig. 9.36a)

and will be determined from the condition that the slope of the beam at

A must be zero. The solution is carried out by considering separately the

slope (u

)

caused at A by the uniformly distributed load w (Fig. 9.36b)

and the slope (u

)

produced at the same point by the unknown couple

(Fig 9.36c).

(a)

(b)

(c)

 0



(

)



(

)



Fig. 9.36

Using the table of Appendix D (cases 6 and 7), and noting that in

case 7, A and B must be interchanged, we find that

24E

1u

Writing that the slope at A is the sum of these two quantities and that it

must be zero, we have

5 0

and, solving for M

M

The values of R

and R

may then be found from the equilibrium equa-

tions (9.52) and (9.53).

584

bee80288_ch09_548-629.indd Page 584 10/30/10 11:22:02 PM user-f499bee80288_ch09_548-629.indd Page 584 10/30/10 11:22:02 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

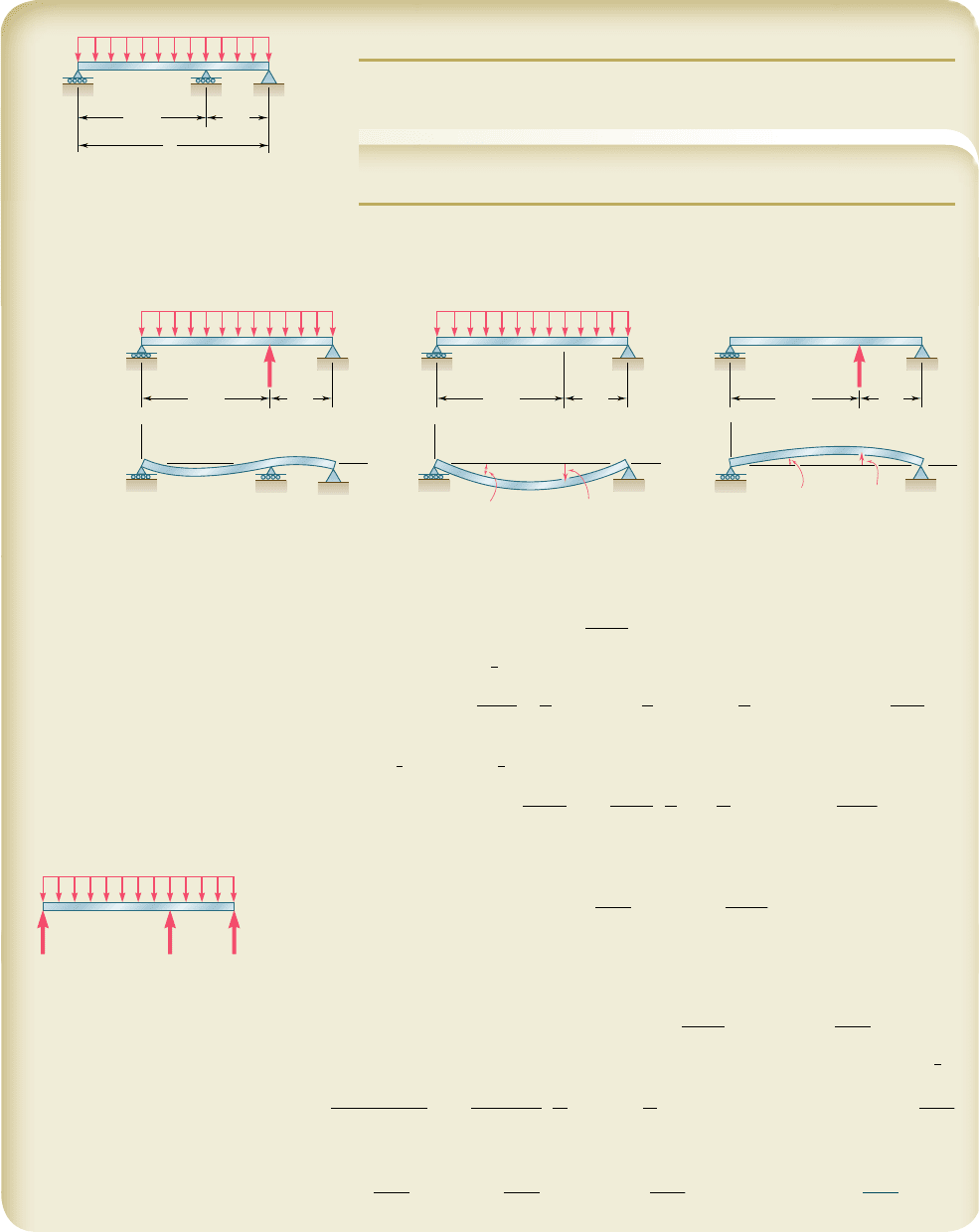
SAMPLE PROBLEM 9.7

For the beam and loading shown, determine the slope and deflection at

point B.

SOLUTION

Principle of Superposition. The given loading can be obtained by

superposing the loadings shown in the following “picture equation.” The

beam AB is, of course, the same in each part of the figure.

L/2 L/2

Loading I

Loading II

L/2 L/2



)

(

)



(

)



)

Loading I

Loading II

)

(

)



L/2 L/2

(

)



(

)

For each of the loadings I and II, we now determine the slope and deflection

at B by using the table of Beam Deflections and Slopes in Appendix D.

Loading I

6EI

8EI

Loading II

w1L

6EI

48EI

w1L

8EI

128EI

In portion CB, the bending moment for loading II is zero and thus the

elastic curve is a straight line.

5 1u

48EI

5 1y

1 1u

8EI

48EI

7wL

384EI

Slope at Point B

5 1u

1 1u

6EI

48EI

7wL

48EI

7wL

48EI

cb

Deflection at B

5 1y

1 1y

8EI

7wL

384EI

41wL

384EI

41wL

384EI

w>

585

bee80288_ch09_548-629.indd Page 585 11/18/10 8:57:12 PM user-f499bee80288_ch09_548-629.indd Page 585 11/18/10 8:57:12 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

586

SAMPLE PROBLEM 9.8

For the uniform beam and loading shown, determine (a) the reaction at

each support, (b) the slope at end A.

SOLUTION

Principle of Superposition. The reaction R

is designated as redundant

and considered as an unknown load. The deflections due to the distributed

load and to the reaction R

are considered separately as shown below.

2L/3 L/3

BAC

2L/3 L/3

 0]

)

(

)



)

(

)



 0.271 wL R

 0.688 wL

 0.0413 wL

For each loading the deflection at point B is found by using the table of

Beam Deflections and Slopes in Appendix D.

Distributed Loading. We use case 6, Appendix D

4EI

2 2L x

1 L

At point B, x 5

24EI

2 2L a

1 L

Lbd520.01132

Redundant Reaction Loading. From case 5, Appendix D, with

L and b 5

L, we have

3EIL

5 0.01646

a. Reactions at Supports. Recalling that y

5 0, we write

5 1y

1 1y

0 520.01132

1 0.01646

5 0.688wL

b

Since the reaction R

is now known, we may use the methods of statics to

determine the other reactions: R

5 0.271wL

R

5 0.0413wL

>

b. Slope at End A. Referring again to Appendix D, we have

Distributed Loading.

4EI

520.04167

Redundant Reaction Loading. For P 52R

520.688wL and b 5

Pb1L

2 b

6EIL

0.688w

6EIL

bcL

2 a

5 0.03398

Finally, u

520.04167

1 0.03398

520.00769

5 0.00769

cb

2L/3

L/3

bee80288_ch09_548-629.indd Page 586 10/30/10 11:22:13 PM user-f499bee80288_ch09_548-629.indd Page 586 10/30/10 11:22:13 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09