Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
607
*9.13 MAXIMUM DEFLECTION
When a simply supported or overhanging beam carries an unsym-
metric load, the maximum deflection generally does not occur at
the center of the beam. This will be the case for the beams used
in the bridge shown in Photo 9.5, which is being crossed by the
truck.
9.13 Maximum Defl ection
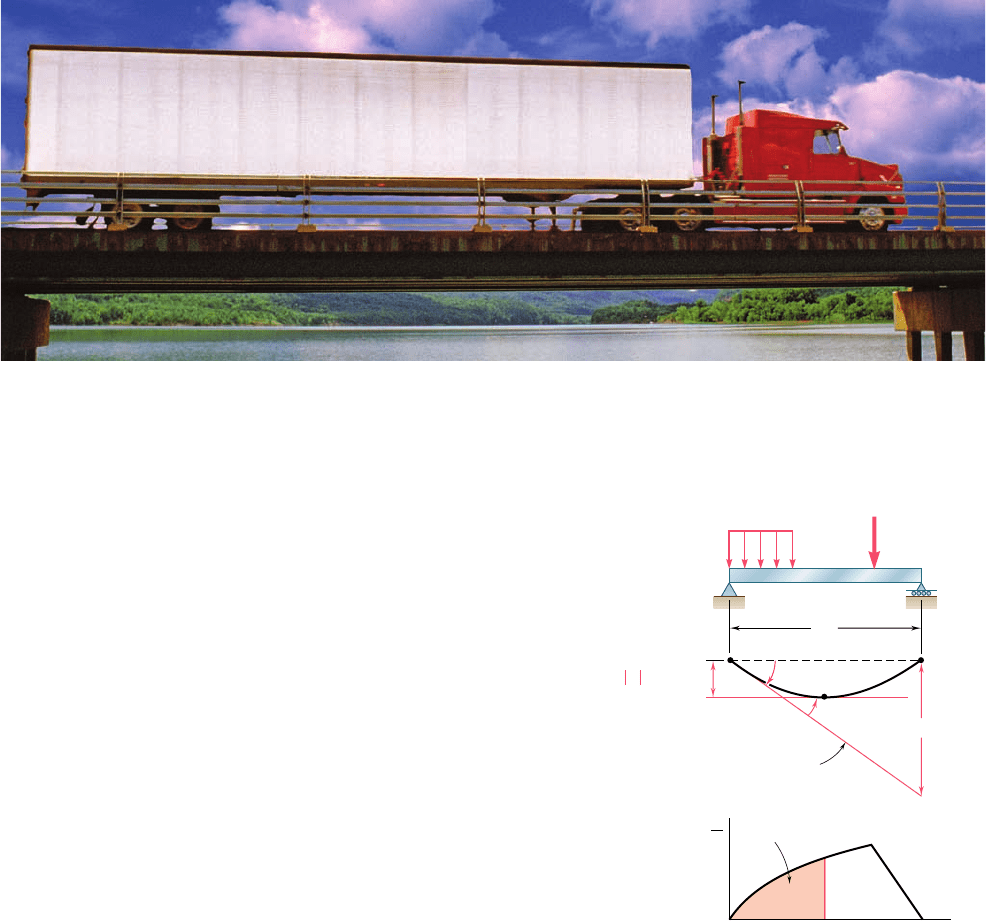
Photo 9.5 The deflections of the beams used for the bridge must be reviewed for different possible positions of the truck.
To determine the maximum deflection of such a beam, we
should locate the point K of the beam where the tangent is horizon-
tal, and compute the deflection at that point.
Our analysis must begin with the determination of a reference
tangent at one of the supports. If support A is selected, the slope u
A
of the tangent at A is obtained by the method indicated in the pre-
ceding section, i.e., by computing the tangential deviation t
ByA
of
support B with respect to A and dividing that quantity by the dis-
tance L between the two supports.
Since the slope u
K
at point K is zero (Fig. 9.63a), we must
have
u
K
y
A
5 u
K
2 u
A
5 0 2 u
A
52u
A
Recalling the first moment-area theorem, we conclude that point K
may be determined by measuring under the (MyEI) diagram an area
equal to u
KyA
5 2u
A
(Fig. 9.63b).
Observing that the maximum deflection |y|
max
is equal to the
tangential deviation t
AyK
of support A with respect to K (Fig. 9.63a),
we can obtain |y|
max
by computing the first moment with respect
to the vertical axis through A of the area between A and K
(Fig. 9.63b).
P
A
A
w
B
B
K
L
0
0
(a)
AKB
x
(b)
A
K
K/A
A
K/A
t
B/A
Reference
target
Area
M
EI
y
max
t
A /K
Fig. 9.63 Determination of maximum
deflection using moment-area method.
bee80288_ch09_548-629.indd Page 607 10/30/10 11:25:56 PM user-f499bee80288_ch09_548-629.indd Page 607 10/30/10 11:25:56 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
EXAMPLE 9.13
Determine the maximum deflection of the beam of Example 9.12.
Determination of Point K Where Slope Is Zero. We recall from
Example 9.12 that the slope at point D, where the load is applied, is negative.
It follows that point K, where the slope is zero, is located between D and
the support B (Fig. 9.64). Our computations, therefore, will be simplified if
we relate the slope at K to the slope at B, rather than to the slope at A.
Since the slope at A has already been determined in Example 9.12,
the slope at B is obtained by writing
u
B
5 u
A
1 u
B
y
A
5 u
A
1
A
1
1
A
2
u
B
52
7PL
2
128EI
1
3PL
2
128EI
1
9PL
2
128EI
5
5PL
2
128EI
Observing that the bending moment at a distance u from end B is M 5
1
4
Pu
(Fig. 9.65a), we express the area A9 located between K and B under the
(MyEI) diagram (Fig. 9.65b) as
A
¿ 5
1
2
Pu
4EI
u 5
Pu
2
8EI
By the first moment-area theorem, we have
u
B
y
K
5 u
B
2 u
K
5 A
¿
and, since u
K
5 0, u
B
5 A9
Substituting the values obtained for u
B
and A9, we write
5PL
2
128EI
5
Pu
2
8EI
and, solving for u,
u 5
1
5
4
L 5 0.559L
Thus, the distance from the support A to point K is
AK 5 L 2 0.559L 5 0.441L
Maximum Deflection. The maximum deflection |y|
max
is equal to
the tangential deviation t
ByK
and, thus, to the first moment of the area A9
about a vertical axis through B (Fig. 9.65b). We write
0y 0
max
5 t
B
y
K
5 A¿
a
2u
3
b
5
Pu
2
8EI
a
2u
3
b
5
Pu
3
12EI
Substituting the value obtained for u, we have
0y 0
max
5
P
12EI
a
15
4
L
b
3
5 0.01456PL
3
/EI
B
D
L
A
1
A
2
A
D
B
x
EI
M
P
A
R
A
3P
4
1
4
3L
4
R
B
P
4
E
D
K
A
K
0
B
A
B
y
max
t
B /K
Fig. 9.64
R
B
M
V
P
4
K
B
u
(a)
Fig. 9.65
A'
A
D
K
B
x
EI
M
4EI
Pu
u
(b)
608
bee80288_ch09_548-629.indd Page 608 10/30/10 11:26:01 PM user-f499bee80288_ch09_548-629.indd Page 608 10/30/10 11:26:01 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
609
*9.14 USE OF MOMENT-AREA THEOREMS WITH
STATICALLY INDETERMINATE BEAMS
The reactions at the supports of a statically indeterminate beam can
be determined by the moment-area method in much the same way
that was described in Sec. 9.8. In the case of a beam indeterminate
to the first degree, for example, we designate one of the reactions
as redundant and eliminate or modify accordingly the corresponding
support. The redundant reaction is then treated as an unknown load,
which, together with the other loads, must produce deformations
that are compatible with the original supports. The compatibility
condition is usually expressed by writing that the tangential deviation
of one support with respect to another either is zero or has a pre-
determined value.
Two separate free-body diagrams of the beam are drawn. One
shows the given loads and the corresponding reactions at the sup-
ports that have not been eliminated; the other shows the redundant
reaction and the corresponding reactions at the same supports (see
Example 9.14). An MyEI diagram is then drawn for each of the two
loadings, and the desired tangential deviations are obtained by the
second moment-area theorem. Superposing the results obtained, we
express the required compatibility condition and determine the
redundant reaction. The other reactions are obtained from the free-
body diagram of beam.
Once the reactions at the supports have been determined, the
slope and deflection may be obtained by the moment-area method
at any other point of the beam.
9.14 Use of Moment-Area Theorems with
Statically Indeterminate Beams
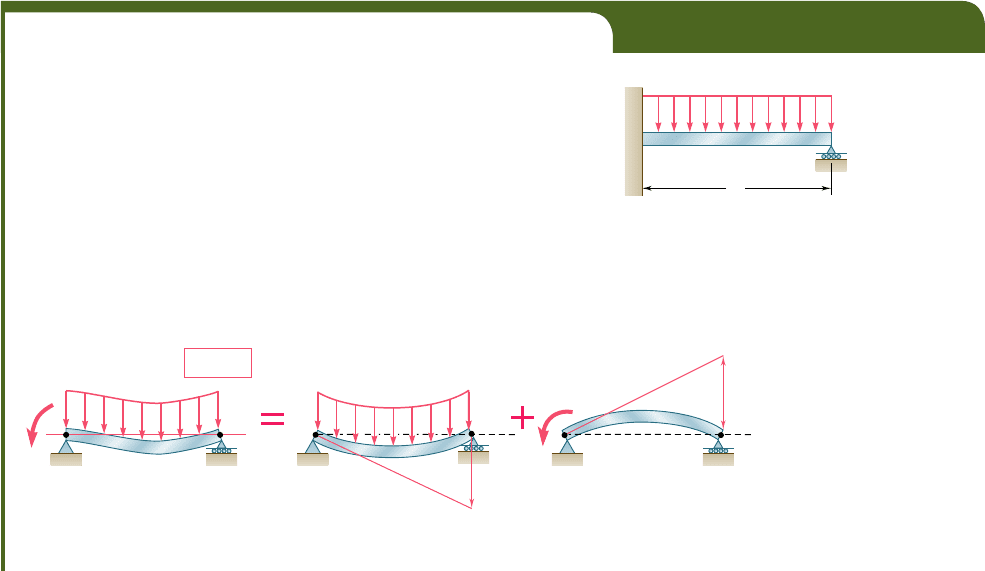
EXAMPLE 9.14
Determine the reaction at the supports for the prismatic beam and load-
ing shown (Fig. 9.66).
We consider the couple exerted at the fixed end A as redundant
and replace the fixed end by a pin-and-bracket support. The couple M
A
is now considered as an unknown load (Fig. 9.67a) and will be deter-
mined from the condition that the tangent to the beam at A must be
horizontal. It follows that this tangent must pass through the support
B and, thus, that the tangential deviation t
ByA
of B with respect to A
must be zero. The solution is carried out by computing separately the
tangential deviation (t
ByA
)
w
caused by the uniformly distributed load w
(Fig. 9.67b) and the tangential deviation (t
ByA
)
M
produced by the
unknown couple M
A
(Fig. 9.67c).
B
w
A
L
Fig. 9.66
A
A
w
w
B
B
AB
M
A
M
A
t
B/A
0
B''
B'
(t
B/A
)
w
(t
B/A
)
M
(a)(b)(c)
Fig. 9.67
bee80288_ch09_548-629.indd Page 609 10/30/10 11:26:06 PM user-f499bee80288_ch09_548-629.indd Page 609 10/30/10 11:26:06 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
Considering first the free-body diagram of the beam under the
known distributed load w (Fig. 9.68a), we determine the corresponding
reactions at the supports A and B. We have
1
R
A
2
1
5
1
R
B
2
1
5
1
2
wLx (9.64)
We can now draw the corresponding shear and (MyEI) diagrams (Figs.
9.68b and c). Observing that MyEI is represented by an arc of parabola,
and recalling the formula,
A
5
2
3
bh, for the area under a parabola, we
compute the first moment of this area about a vertical axis through B and
write
1t
B
y
A
2
w
5 A
1
a
L
2
b
5
a
2
3
L
wL
2
8EI
b
a
L
2
b
5
wL
4
24EI
(9.65)
Considering next the free-body diagram of the beam when it is
subjected to the unknown couple M
A
(Fig. 9.69a), we determine the cor-
responding reactions at A and B:
1R
A
2
2
5
M
A
L
x
1R
B
2
2
5
M
A
L
w
(9.66)
Drawing the corresponding (MyEI) diagram (Fig. 9.69b), we apply again
the second moment-area theorem and write
1t
B
y
A
2
M
5 A
2
a
2L
3
b
5
a
2
1
2
L
M
A
EI
b
a
2L
3
b
52
M
A
L
2
3EI
(9.67)
Combining the results obtained in (9.65) and (9.67), and expressing
that the resulting tangential deviation t
ByA
must be zero (Fig. 9.67), we
have
t
B
y
A
5
1
t
B
y
A
2
w
1
1
t
B
y
A
2
M
5 0
wL
4
24E
I
2
M
A
L
2
3
E
I
5 0
and, solving for M
A
,
M
A
51
1
8
wL
2
M
A
5
1
8
wL
2
l
Substituting for M
A
into (9.66), and recalling (9.64), we obtain the values
of R
A
and R
B
:
R
A
5
1
R
A
2
1
1
1
R
A
2
2
5
1
2
wL 1
1
8
wL 5
5
8
wL
R
B
5
1
R
B
2
1
1
1
R
B
2
2
5
1
2
wL 2
1
8
wL 5
3
8
wL
610
(a)
(b)
(c)
B
B
x
x
w
A
A
B
L
A
A
1
L
V
(R
B
)
1
(R
A
)
1
wL
1
2
wL
1
2
L
2
L
2
wL
2
M
EI
8EI
wL
1
8
(
2
)
Fig. 9.68
M
A
(a)
(b)
B
A
L
x
(R
B
)
2
(R
A
)
2
A
2
M
A
EI
2L
3
B
A
M
EI
Fig. 9.69
In the example we have just considered, there was a single
redundant reaction, i.e., the beam was statically indeterminate to the
first degree. The moment-area theorems can also be used when there
are additional redundant reactions. As discussed in Sec. 9.5, it is then
necessary to write additional equations. Thus for a beam that is stati-
cally indeterminate to the second degree, it would be necessary to
select two redundants and write two equations considering the defor-
mations of the structure involved.
bee80288_ch09_548-629.indd Page 610 11/18/10 8:58:23 PM user-f499bee80288_ch09_548-629.indd Page 610 11/18/10 8:58:23 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
611
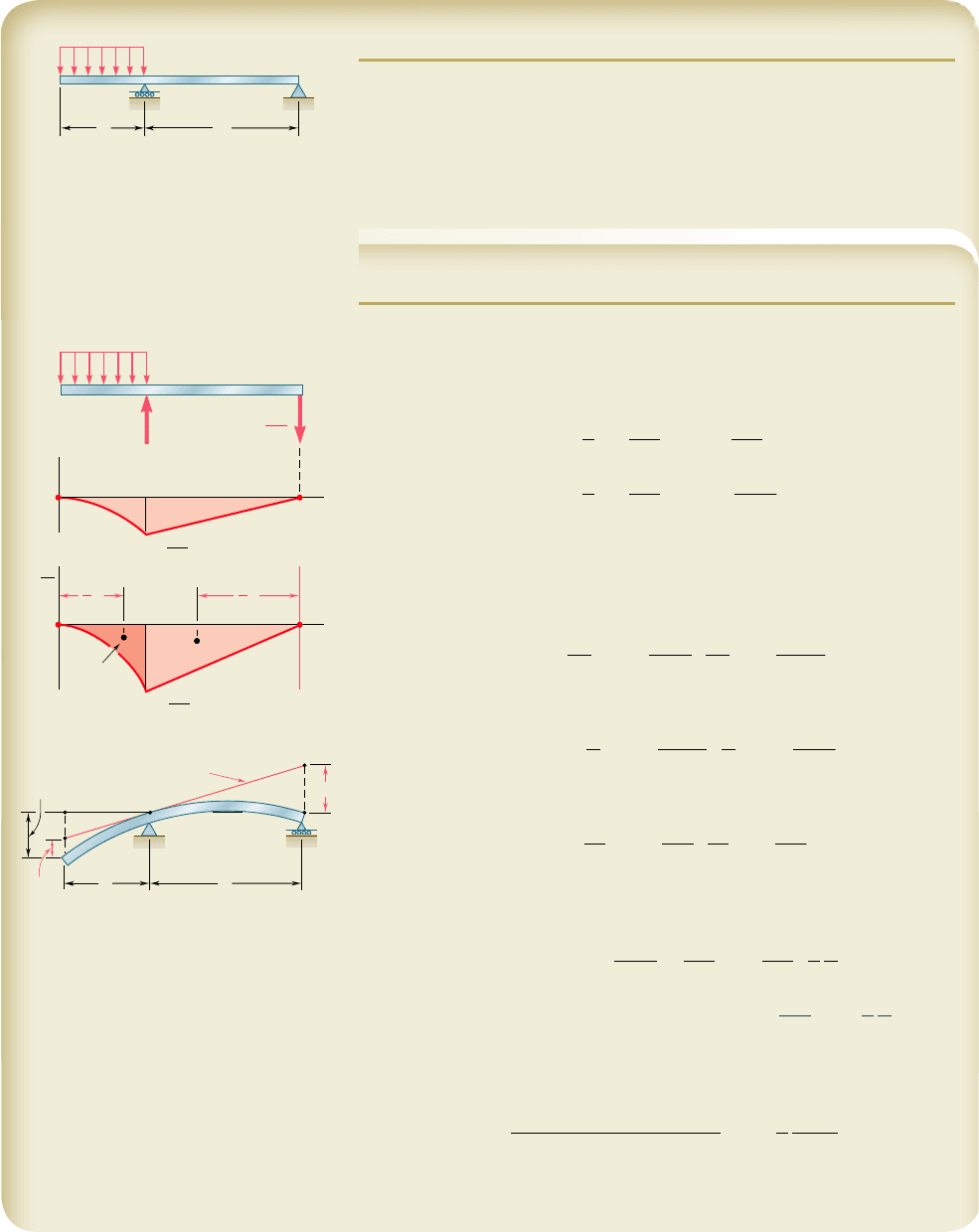
SAMPLE PROBLEM 9.12
For the beam and loading shown, (a) determine the deflection at end A,
(b) evaluate y
A
for the following data:
W10 3 33: I 5 171 in
4
E 5 29 3 10
6
psi
a 5 3 ft 5 36 in. L 5 5.5 ft 5 66 in.
w 5 13.5 kips/ft 5 1125 lb/in.
SOLUTION
(MyEI) Diagram. We first draw the bending-moment diagram.
Since the flexural rigidity EI is constant, we obtain the (MyEI) diagram
shown, which consists of a parabolic spandrel of area A
1
and a triangle
of area A
2
.
A
1
5
1
3
a
2
wa
2
2EI
b
a 52
wa
3
6EI
A
2
5
1
2
a
2
wa
2
2EI
b
L 52
wa
2
L
4EI
Reference Tangent at B. The reference tangent is drawn at point B
as shown. Using the second moment-area theorem, we determine the tan-
gential deviation of C with respect to B:
t
C
y
B
5 A
2
2
L
3
5
a
2
wa
2
L
4EI
b
2
L
3
52
wa
2
L
2
6EI
From the similar triangles A0A9B and CC9B, we find
A
–A¿ 5 t
C
y
B
a
a
L
b
52
wa
2
L
2
6EI
a
a
L
b
52
wa
3
L
6EI
Again using the second moment-area theorem, we write
t
A
y
B
5 A
1
3
a
4
5
a
2
wa
3
6EI
b
3
a
4
52
wa
4
8EI
a. Deflection at End A
y
A
5 A–A¿ 1 t
A/B
52
wa
3
L
6EI
2
wa
4
8EI
52
wa
4
8EI
a
4
3
L
a
1 1
b
y
A
5
wa
4
8EI
a
1 1
4
3
L
a
b
w b
b. Evaluation of y
A
. Substituting the data given, we write
y
A
5
11125 lb/in.2136 in.2
4
8
1
29 3 10
6
lb/in
2
21
171 in
4
2
a1 1
4
3
66 in.
36 in.
b
y
A
5 0.1641 in.w b
B
w
A
L
C
a
B
C
wa
2
2EI
wa
2
2
wa
2
2L
a
3
4
A
x
M
EI
B
w
C
A
1
A
2
x
M
L
2
3
R
B
R
C
A⬘⬘
A⬘
A
y
A
C⬘
C
B
L
a
Reference tangent
t
C/B
t
A/B
A
bee80288_ch09_548-629.indd Page 611 10/30/10 11:26:16 PM user-f499bee80288_ch09_548-629.indd Page 611 10/30/10 11:26:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
612
SAMPLE PROBLEM 9.13
For the beam and loading shown, determine the magnitude and location of
the largest deflection. Use E 5 200 GPa.
B
A
L 3.6 m
b 2.2 m
a 1.4 m
W250 22.3
w 25 kN/m
w
b
L
L
3
a
R
A
R
B
wb
2
2EI
R
A
L
EI
wb
2
2L
b
4
A
A
x
M
EI
B
B
B
A
A
1
A
2
A
3
R
A
x
m
EI
K
A
4
a
L
Reference tangent
t
B/A
A
x
x
m
(x
m
a)
M
EI
A
w
2EI
(x
m
a)
2
(x
m
a)
1
4
t
A/K
A
y
m
K
B
Reference tangent
A
K/A
[
K
0 ]
SOLUTION
Reactions. Using the free-body diagram of the entire beam, we find
R
A
5 16.81
k
Nx R
B
5 38.2
k
Nx
(MyEI) Diagram. We draw the (MyEI) diagram by parts, considering
separately the effects of the reaction R
A
and of the distributed load. The
areas of the triangle and of the spandrel are
A
1
5
1
2
R
A
L
E
I
L 5
R
A
L
2
2E
I
A
2
5
1
3
a
2
wb
2
2EI
b
b 52
wb
3
6EI
Reference Tangent. The tangent to the beam at support A is chosen
as the reference tangent. Using the second moment-area theorem, we deter-
mine the tangential deviation t
ByA
of support B with respect to support A:
t
B
y
A
5 A
1
L
3
1 A
2
b
4
5
a
R
A
L
2
2EI
b
L
3
1
a
2
wb
3
6EI
b
b
4
5
R
A
L
3
6EI
2
wb
4
24EI
Slope at A
u
A
52
t
B
y
A
L
52
a
R
A
L
2
6EI
2
wb
4
24EIL
b
(1)
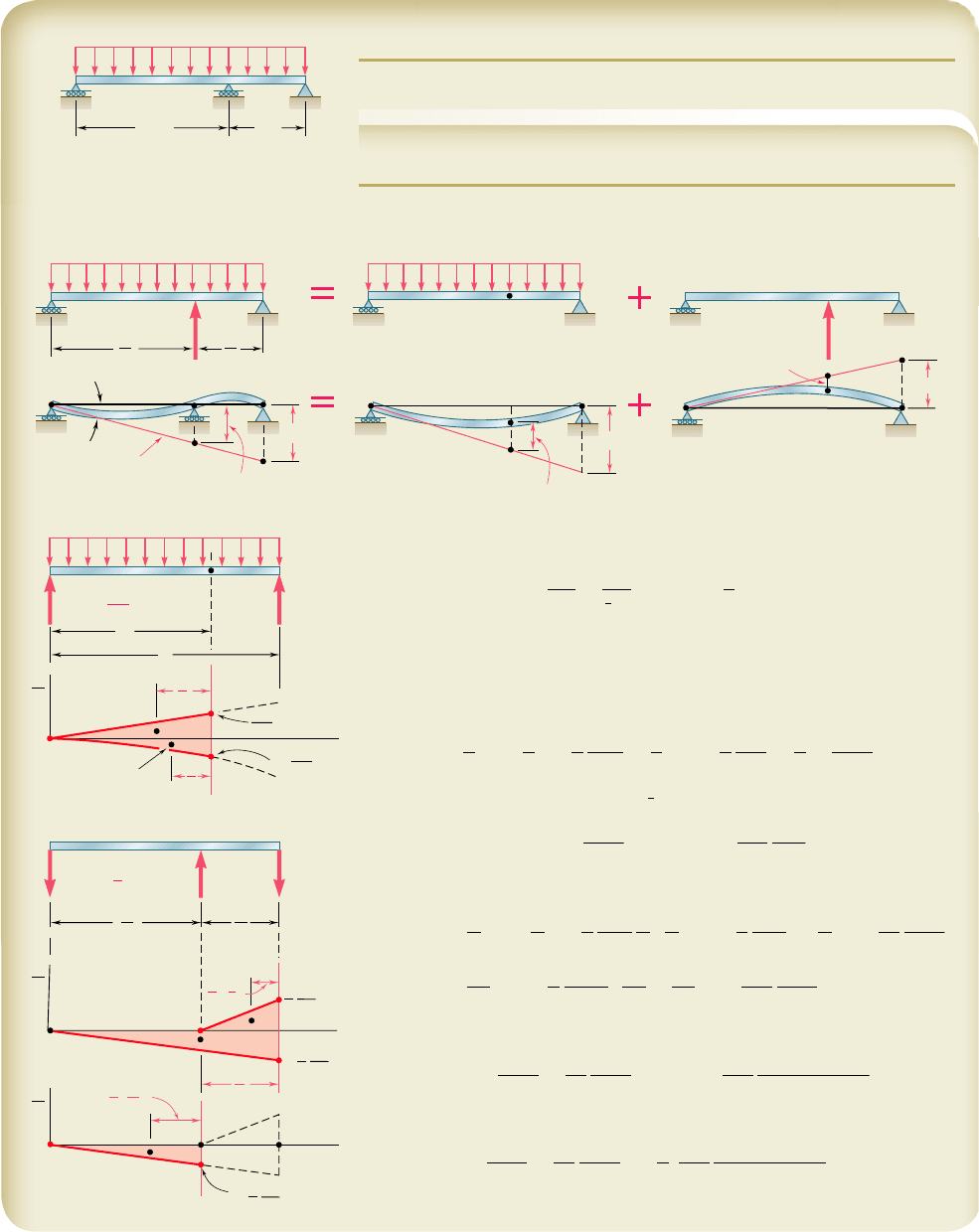
Largest Deflection. The largest deflection occurs at point K, where
the slope of the beam is zero. We write therefore
u
K
5 u
A
1 u
K
y
A
5
0
(2)
But
u
K
y
A
5 A
3
1 A
4
5
R
A
x
2
m
2EI
2
w
6EI
1x
m
2 a2
3
(3)
We substitute for u
A
and u
KyA
from Eqs. (1) and (3) into Eq. (2):
2
a
R
A
L
2
6EI
2
wb
4
24EIL
b
1
c
R
A
x
2
m
2EI
2
w
6EI
1x
m
2 a2
3
d
5 0
Substituting the numerical data, we have
229.53
10
3
E
I
1 8.405x
2
m
10
3
E
I
2 4.1671x
m
2 1.42
3
10
3
E
I
5 0
Solving by trial and error for x
m
, we find x
m
5 1.890 m b
Computing the moments of A
3
and A
4
about a vertical axis through A, we
have
0y 0
m
5 t
A
y
K
5 A
3
2x
m
3
1 A
4
c
a 1
3
4
1x
m
2 a2
d
5
R
A
x
m
3
3EI
2
wa
6EI
1x
m
2 a2
3
2
w
8EI
1x
m
2 a2
4
Using the given data, R
A
5 16.81 kN, and I 5 28.7 3 10
26
m
4
, we find
y
m
5 6.44 mmw b
bee80288_ch09_548-629.indd Page 612 11/18/10 8:58:28 PM user-f499bee80288_ch09_548-629.indd Page 612 11/18/10 8:58:28 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
613
SAMPLE PROBLEM 9.14
For the uniform beam and loading shown, determine the reaction at B.
SOLUTION
The beam is indeterminate to the first degree. we choose the reaction R
B
as redundant and consider separately the distributed loading and the redun-
B
w
A
C
L/32L/3
B
C
w
A
B
B
C
C
w
A
A
B
B
B
C
A
C
C
A
A
2L
3
L
3
R
B
R
B
B'
C'
Reference tangent
t
C/A
t
B/A
(t
B/A
)
w
A
(t
C/A
)
w
(t
C/A
)
R
(t
B/A
)
R
dant reaction loading. We next select the tangent at A as the reference tan-
gent. From the similar triangles ABB9 and ACC9, we find that
t
C
y
A
L
5
t
B
y
A
2
3
L
t
C
y
A
5
3
2
t
B
y
A
(1)
For each loading, we draw the (MyEI) diagram and then determine the
tangential deviations of B and C with respect to A.
Distributed Loading. Considering the (MyEI) diagram from end A to
an arbitrary point X, we write
1t
X
y
A
2
w
5 A
1
x
3
1 A
2
x
4
5
a
1
2
wLx
2EI
x
b
x
3
1
a
2
1
3
wx
2
2EI
x
b
x
4
5
wx
3
24EI
12L 2 x2
Letting successively x 5 L and
x
5
2
3
L, we have
1t
C
y
A
2
w
5
wL
4
24E
I
1t
B
y
A
2
w
5
4
24
3
wL
4
E
I
Redundant Reaction Loading
1t
C
y
A
2
R
5 A
3
L
9
1 A
4
L
3
5
a
1
2
R
B
L
3EI
L
3
b
L
9
1
a
2
1
2
R
B
L
3EI
L
b
L
3
52
4
81
R
B
L
3
EI
1t
B
y
A
2
R
5 A
5
2L
9
5
c
2
1
2
2R
B
L
9EI
a
2L
3
bd
2L
9
52
4
243
R
B
L
3
EI
Combined Loading. Adding the results obtained, we write
t
C
y
A
5
wL
4
24EI
2
4
81
R
B
L
3
EI
t
B
y
A
5
4
24
3
1wL
4
2 R
B
L
3
2
E
I
Reaction at B. Substituting for t
CyA
and t
ByA
into Eq. (1), we have
a
wL
4
24EI
2
4
81
R
B
L
3
EI
b
5
3
2
c
4
243
1wL
4
2 R
B
L
3
2
EI
d
R
B
5 0.6875wL R
B
5 0.688wLx b
(R
A
)
1
(R
C
)
1
(R
C
)
2
(R
A
)
2
R
B
R
B
B
C
C
X
X
x
x
x
x
x
L
w
A
A
A
A
A
A
5
A
4
A
3
C
C
B
B
wL
2
1
3
wLx
2EI
3
x
4
M
EI
M
EI
M
EI
A
1
A
2
2L
3
L
3
L
3
wx
2
2EI
R
B
L
EI
2
9
R
B
L
EI
1
3
R
B
L
EI
1
3
L
3
1
3
2L
3
1
3
(
)
()
bee80288_ch09_548-629.indd Page 613 11/18/10 8:58:37 PM user-f499bee80288_ch09_548-629.indd Page 613 11/18/10 8:58:37 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
PROBLEMS
614
Use the moment-area method to solve the following
problems.
9.125 through 9.128 For the prismatic beam and loading shown,
determine (a) the deflection at point D, (b) the slope at end A.
DE
B
A
PP
L/2 L/4
L/4
Fig. P9.125
B
D
A
M
0
L
3
2L
3
Fig. P9.126
A
B
D
w
0
L/2
L
Fig. P9.127
L/2
w
D
B
L
A
Fig. P9.128
9.129 and 9.130 For the beam and loading shown, determine (a) the
slope at end A, (b) the deflection at point D. Use E 5 200 GPa.
A
B
DC
1.5 m 1.5 m
3.0 m
W250 44.8
40 kN 20 kN
Fig. P9.129
A
D
1.6 m
0.8 m
B
30 kN
20 kN/m
W150 24
Fig. P9.130
9.131 For the beam and loading shown, determine (a) the slope at point A,
(b) the deflection at point E. Use E 5 29 3 10
6
psi.
AB
D
E
W12 26
2 ft 4 ft 4 ft
5 kips/ft
8 kips/ft
Fig. P9.131
2 ft 2 ft
800 lb
200 lb/ft
4 ft
6 in.
2 in.
DA
B
C
Fig. P9.132
9.132 For the timber beam and loading shown, determine (a) the slope
at point A, (b) the deflection at point C. Use E 5 1.7 3 10
6
psi.
bee80288_ch09_548-629.indd Page 614 11/1/10 8:41:11 PM user-f499bee80288_ch09_548-629.indd Page 614 11/1/10 8:41:11 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
615
Problems
9.133 For the beam and loading shown, determine (a) the slope at point A,
(b) the deflection at point D.
D
CB
P
A
L/2 L/2 L/2
P
Fig. P9.133
M
0
AC
B
aL
Fig. P9.134
9.134 For the beam and loading shown, determine (a) the slope at point A,
(b) the deflection at point A.
9.135 For the beam and loading shown, determine (a) the slope at point C,
(b) the deflection at point D. Use E 5 29 3 10
6
psi.
8 kips/ft
B
D
C
A
4 ft
6 ft6 ft
W12 30
16 kips
Fig. P9.135
W410 114
4.8 m
A
D
B
40 kN/m
160 kN
1.8 m
Fig. P9.136
9.136 For the beam and loading shown, determine (a) the slope at point B,
(b) the deflection at point D. Use E 5 200 GPa.
9.137 Knowing that the beam AB is made of a solid steel rod of diameter
d 5 0.75 in., determine for the loading shown (a) the slope at point D,
(b) the deflection at point A. Use E 5 29 3 10
6
psi.
150 lb 300 lb
DE
BA
d
24 in.
4 in. 6 in.
Fig. P9.137
D
B
C
1.2 kN
3 kN/m
0.25 m
0.20 m
0.25 m
A
30 mm
30 mm
Fig. P9.138
9.138 Knowing that the beam AD is made of a solid steel bar, determine
(a) the slope at point B, (b) the deflection at point A. Use E 5
200 GPa.
bee80288_ch09_548-629.indd Page 615 10/30/10 11:26:56 PM user-f499bee80288_ch09_548-629.indd Page 615 10/30/10 11:26:56 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
616
Defl ection of Beams
9.139 For the beam and loading shown, determine the deflection (a) at
point D, (b) at point E.
A
C
L
B
P
L/2
Fig. P9.148
B
A
w
0
L
Fig. P9.147
L/2 L/2
C
A
B
w
Fig. P9.149
L/2
A
M
0
C
L
B
Fig. P9.150
L/2 L/2
A
C
w
B
EI
2EI
Fig. P9.140
B
D
E
A
L/3 L/3
2EI2EI
EI
L/3
PP
Fig. P9.139
9.141 through 9.144 For the beam and loading shown, determine
the magnitude and location of the largest downward deflection.
9.141 Beam and loading of Prob. 9.125
9.142 Beam and loading of Prob. 9.127
9.143 Beam and loading of Prob. 9.129
9.144 Beam and loading of Prob. 9.131
9.145 For the beam and loading of Prob. 9.136, determine the largest
upward deflection in span AB.
9.146 For the beam and loading of Prob. 9.137, determine the largest
upward deflection in span DE.
9.147 through 9.150 For the beam and loading shown, determine
the reaction at the roller support.
9.140 For the beam and loading shown, determine (a) the slope at end A,
(b) the slope at end B, (c) the deflection at the midpoint C.
bee80288_ch09_548-629.indd Page 616 10/30/10 11:27:11 PM user-f499bee80288_ch09_548-629.indd Page 616 10/30/10 11:27:11 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
