Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

627

COMPUTER PROBLEMS

The following problems are designed to be solved with a computer.

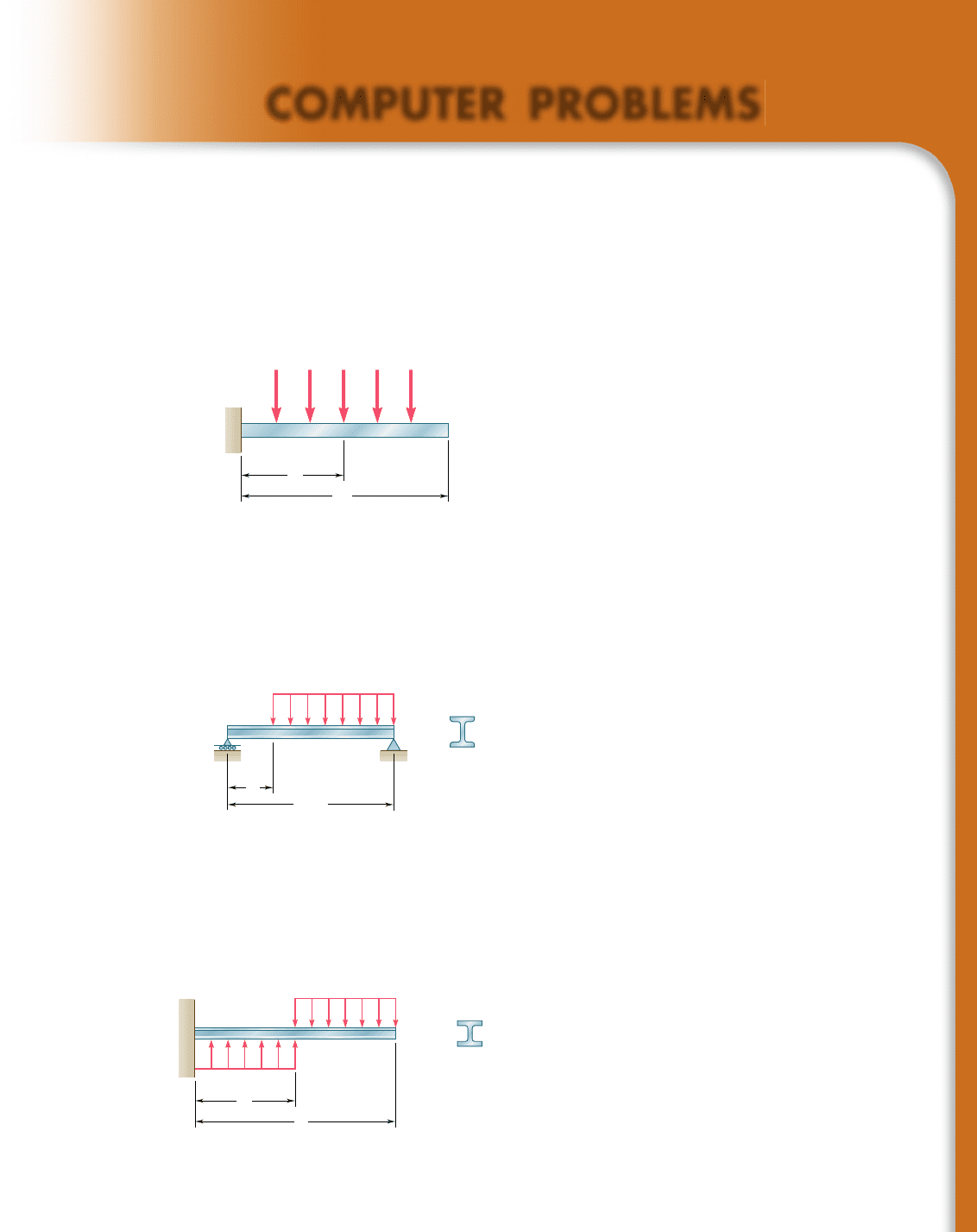
9.C1 Several concentrated loads can be applied to the cantilever beam AB.

Write a computer program to calculate the slope and deflection of beam

AB from x 5 0 to x 5 L, using given increments Dx. Apply this program

with increments Dx 5 50 mm to the beam and loading of Prob. 9.73 and

Prob. 9.74.

Fig. P9.C1

9.C2 The 22-ft beam AB consists of a W21 3 62 rolled-steel shape and

supports a 3.5-kip/ft distributed load as shown. Write a computer program

and use it to calculate for values of a from 0 to 22 ft, using 1-ft increments,

(a) the slope and deflection at D, (b) the location and magnitude of the

maximum deflection. Use E 5 29 3 10

psi.

3.5 kips/ft

22 ft

Fig. P9.C2

9.C3 The cantilever beam AB carries the distributed loads shown. Write a

computer program to calculate the slope and deflection of beam AB from

x 5 0 to x 5 L using given increments D x. Apply this program with increments

D x 5 100 mm, assuming that L 5 2.4 m, w 5 36 kN/m, and (a) a 5 0.6 m,

(b) a 5 1.2 m, (c) a 5 1.8 m. Use E 5 200 GPa.

W250  32.7

Fig. P9.C3

bee80288_ch09_548-629.indd Page 627 11/18/10 8:58:52 PM user-f499bee80288_ch09_548-629.indd Page 627 11/18/10 8:58:52 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

628

Deﬂ ection of Beams

9.C4 The simple beam AB is of constant flexural rigidity EI and carries

several concentrated loads as shown. Using the Method of Integration, write

a computer program that can be used to calculate the slope and deflection

at points along the beam from x 5 0 to x 5 L using given increments D x.

Apply this program to the beam and loading of (a) Prob. 9.13 with D x 5 1 ft,

(b) Prob. 9.16 with D x 5 0.05 m, (c) Prob. 9.129 with D x 5 0.25 m.

Fig. P9.C4

9.C5 The supports of beam AB consist of a fixed support at end A and

a roller support located at point D. Write a computer program that can be

used to calculate the slope and deflection at the free end of the beam for

values of a from 0 to L using given increments Da. Apply this program to

calculate the slope and deflection at point B for each of the following

cases:

L DL w E Shape

(a) 12 ft 0.5 ft 1.6 k/ft 29 3 10

psi W16 3 57

(b) 3 m 0.2 m 18 kN/m 200 GPa W460 3 113

Fig. P9.C5

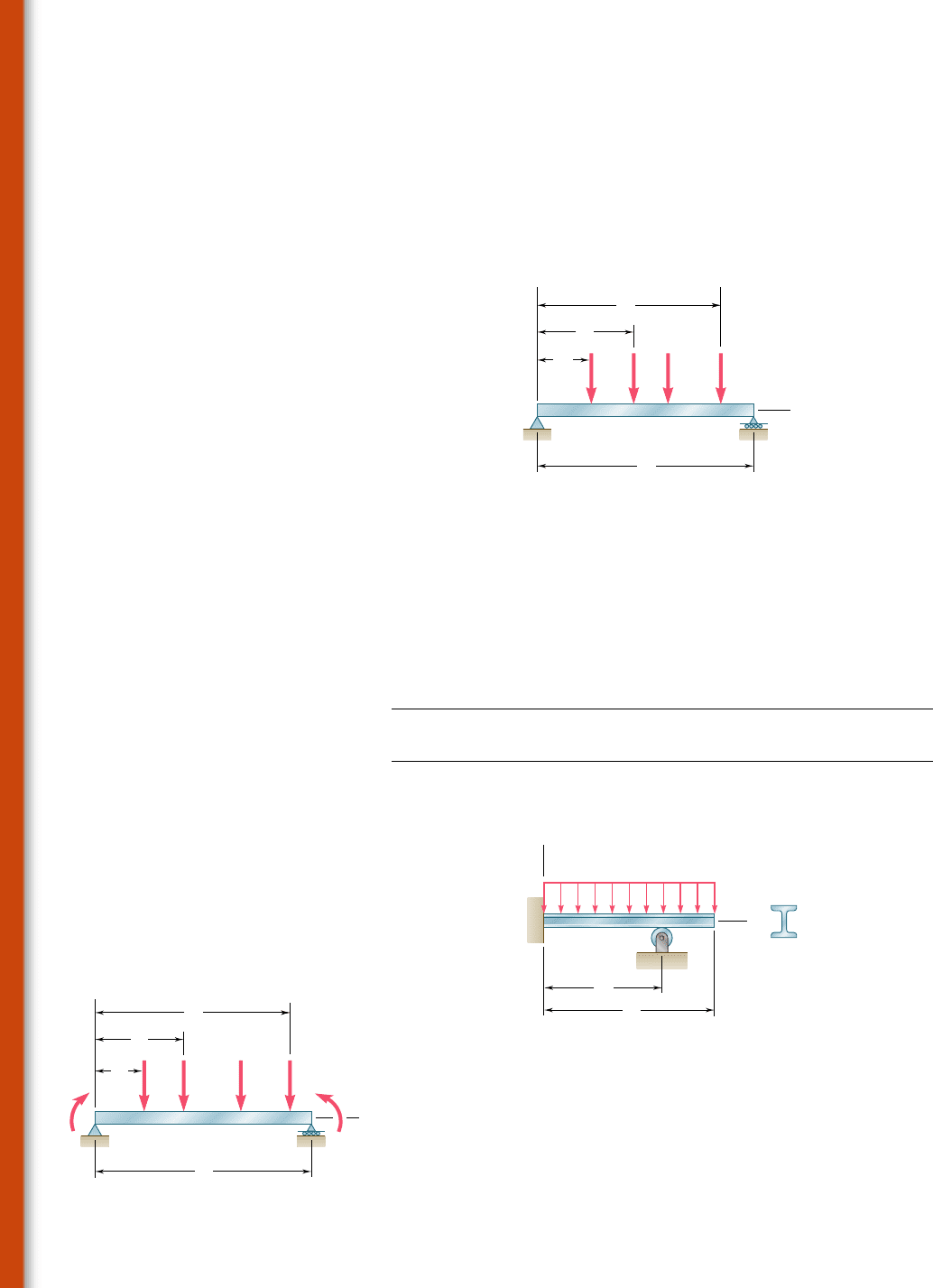
9.C6 For the beam and loading shown, use the Moment-Area Method to

write a computer program to calculate the slope and deflection at points along

the beam from x 5 0 to x 5 L using given increments D x. Apply this program

to calculate the slope and deflection at each concentrated load for the beam

of (a) Prob. 9.77 with D x 5 0.5 m, (b) Prob. 9.119 with D x 5 0.5 m.

Fig. P9.C6

bee80288_ch09_548-629.indd Page 628 11/18/10 8:59:01 PM user-f499bee80288_ch09_548-629.indd Page 628 11/18/10 8:59:01 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

629

Computer Problems

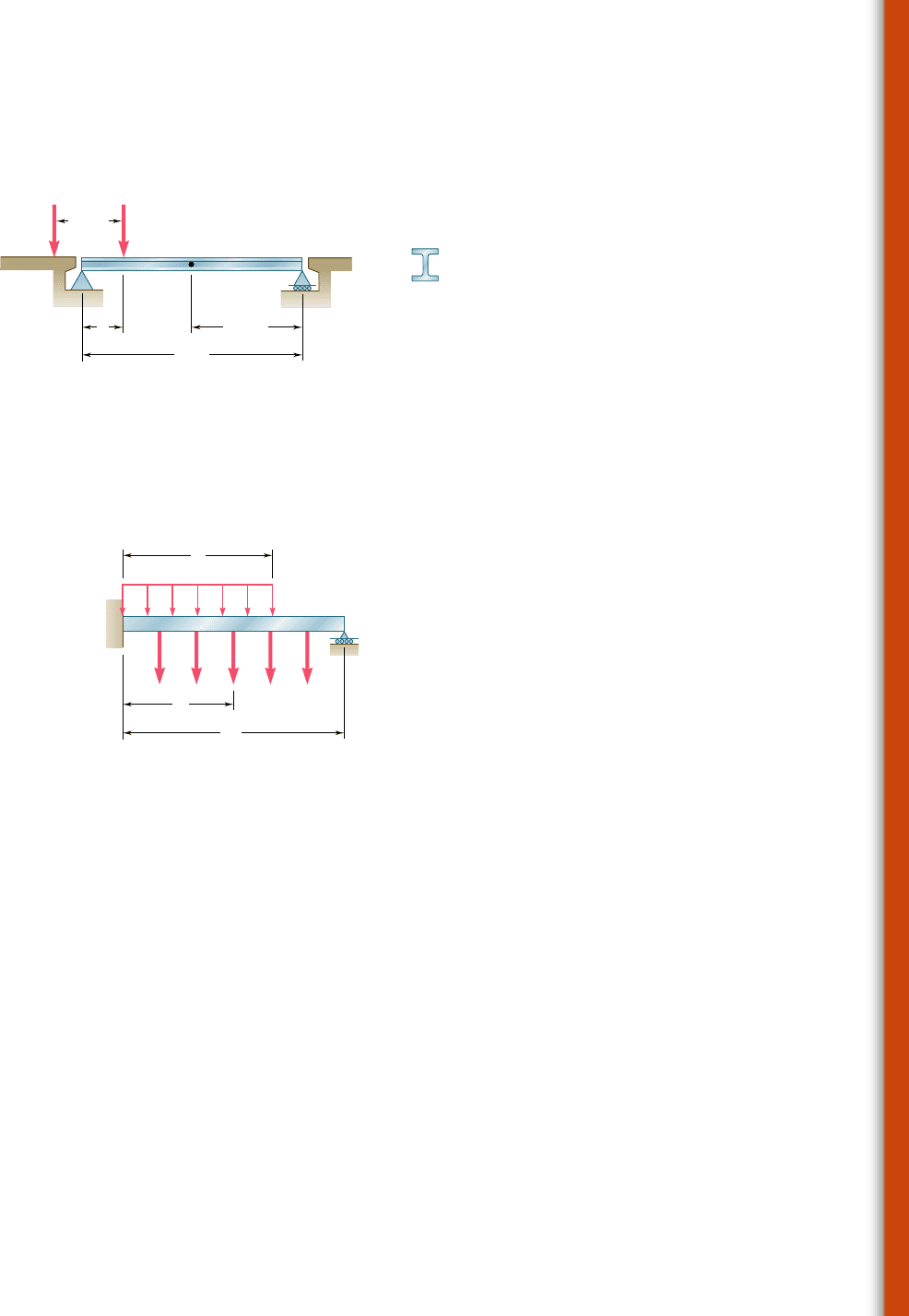
9.C7 Two 52-kN loads are maintained 2.5 m apart as they are moved

slowly across beam AB. Write a computer program to calculate the deflec-

tion at the midpoint C of the beam for values of x from 0 to 9 m, using

0.5-m increments. Use E 5 200 GPa.

x 4.5 m

2.5 m

52 kN 52 kN

9 m

W460  113

Fig. P9.C7

9.C8 A uniformly distributed load w and several distributed loads P

may

be applied to beam AB. Write a computer program to determine the reac-

tion at the roller support and apply this program to the beam and loading

of (a) Prob. 9.53a, (b) Prob. 9.154.

Fig. P9.C8

bee80288_ch09_548-629.indd Page 629 10/30/10 11:30:02 PM user-f499bee80288_ch09_548-629.indd Page 629 10/30/10 11:30:02 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer

The curved pedestrian bridge is

supported by a series of columns.

The analysis and design of members

supporting axial compressive loads will

be discussed in this chapter.

630

bee80288_ch10_630-691.indd Page 630 11/1/10 2:32:26 PM user-f499bee80288_ch10_630-691.indd Page 630 11/1/10 2:32:26 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

Columns

CHAPTER

631

bee80288_ch10_630-691.indd Page 631 11/1/10 2:34:06 PM user-f499bee80288_ch10_630-691.indd Page 631 11/1/10 2:34:06 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

632

Chapter 10 Columns

10.1 Introduction

10.2 Stability of Structures

10.3 Euler’s Formula for Pin-Ended

Columns

10.4 Extension of Euler’s Formula to

Columns with Other End

Conditions

*10.5 Eccentric Loading; the Secant

Formula

10.6 Design of Columns under a

Centric Load

10.7 Design of Columns under an

Eccentric Load

10.1 INTRODUCTION

In the preceding chapters, we had two primary concerns: (1) the

strength of the structure, i.e., its ability to support a specified load

without experiencing excessive stress; (2) the ability of the structure

to support a specified load without undergoing unacceptable defor-

mations. In this chapter, our concern will be with the stability of the

structure, i.e., with its ability to support a given load without experi-

encing a sudden change in its configuration. Our discussion will

relate chiefly to columns, i.e., to the analysis and design of vertical

prismatic members supporting axial loads.

In Sec. 10.2, the stability of a simplified model of a column,

consisting of two rigid rods connected by a pin and a spring and

supporting a load P, will first be considered. You will observe that if

its equilibrium is disturbed, this system will return to its original

equilibrium position as long as P does not exceed a certain value P

called the critical load. However, if P . P

, the system will move

away from its original position and settle in a new position of equi-

librium. In the first case, the system is said to be stable, and in the

second case, it is said to be unstable.

In Sec. 10.3, you will begin the study of the stability of elastic

columns by considering a pin-ended column subjected to a centric

axial load. Euler’s formula for the critical load of the column will be

derived and from that formula the corresponding critical normal

stress in the column will be determined. By applying a factor of

safety to the critical load, you will be able to determine the allowable

load that can be applied to a pin-ended column.

In Sec. 10.4, the analysis of the stability of columns with differ-

ent end conditions will be considered. You will simplify these analyses

by learning how to determine the effective length of a column, i.e.,

the length of a pin-ended column having the same critical load.

In Sec. 10.5, you will consider columns supporting eccentric

axial loads; these columns have transverse deflections for all magni-

tudes of the load. An expression for the maximum deflection under

a given load will be derived and used to determine the maximum

normal stress in the column. Finally, the secant formula which relates

the average and maximum stresses in a column will be developed.

In the first sections of the chapter, each column is initially

assumed to be a straight homogeneous prism. In the last part of

the chapter, you will consider real columns which are designed and

analyzed using empirical formulas set forth by professional orga-

nizations. In Sec. 10.6, formulas will be presented for the allow-

able stress in columns made of steel, aluminum, or wood and

subjected to a centric axial load. In the last section of the chapter

(Sec. 10.7), the design of columns under an eccentric axial load

will be considered.

10.2 STABILITY OF STRUCTURES

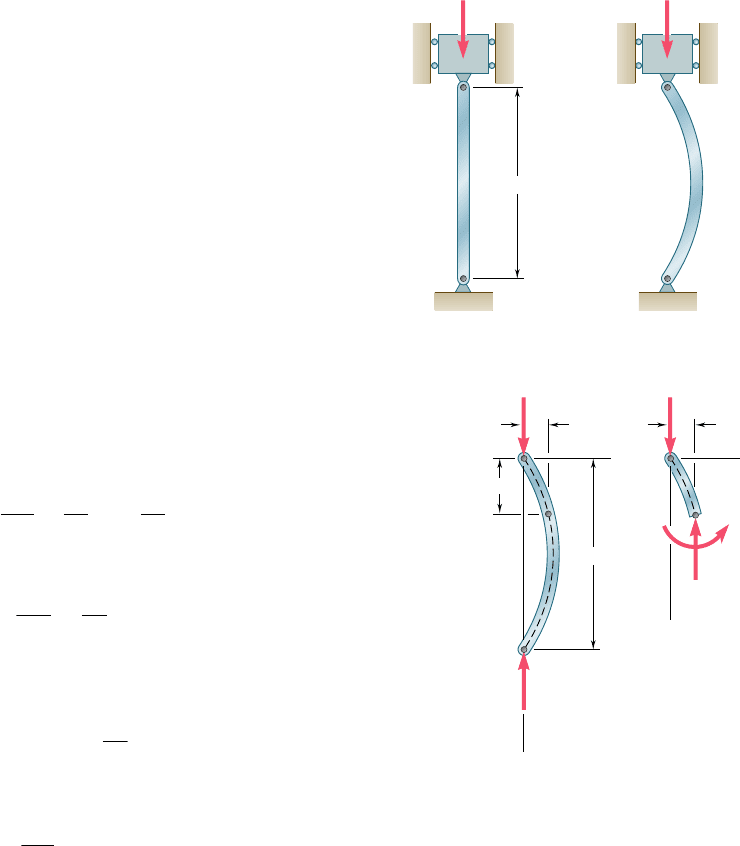
Suppose we are to design a column AB of length L to support a given

load P (Fig. 10.1). The column will be pin-connected at both ends

and we assume that P is a centric axial load. If the cross- sectional

Fig. 10.1 Column.

bee80288_ch10_630-691.indd Page 632 11/19/10 12:57:17 AM user-f499bee80288_ch10_630-691.indd Page 632 11/19/10 12:57:17 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

633

10.2 Stability of Structures

area A of the column is selected so that the value s 5 PyA of the

stress on a transverse section is less than the allowable stress s

all

for

the material used, and if the deformation d 5 PLyAE falls within the

given specifications, we might conclude that the column has been

properly designed. However, it may happen that, as the load is applied,

the column will buckle; instead of remaining straight, it will suddenly

become sharply curved (Fig. 10.2). Photo 10.1 shows a column that

has been loaded so that it is no longer straight; the column has buck-

led. Clearly, a column that buckles under the load it is to support is

not properly designed.

Photo 10.1 Laboratory test showing a buckled column.

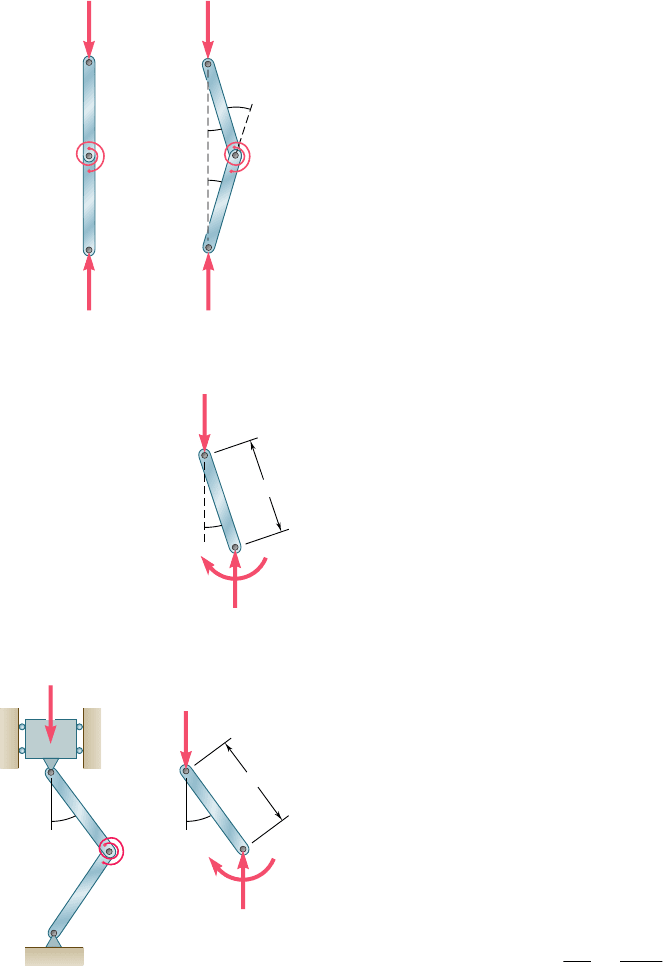
Before getting into the actual discussion of the stability of

elastic columns, some insight will be gained on the problem by

considering a simplified model consisting of two rigid rods AC and

BC connected at C by a pin and a torsional spring of constant K

(Fig. 10.3).

Fig. 10.2 Buckled column.

constant

Fig. 10.3 Column model.

bee80288_ch10_630-691.indd Page 633 11/1/10 2:34:16 PM user-f499bee80288_ch10_630-691.indd Page 633 11/1/10 2:34:16 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

634

Columns

If the two rods and the two forces P and P9 are perfectly

aligned, the system will remain in the position of equilibrium shown

in Fig.10.4a as long as it is not disturbed. But suppose that we move

C slightly to the right, so that each rod now forms a small angle Du

with the vertical (Fig. 10.4b). Will the system return to its original

equilibrium position, or will it move further away from that position?

In the first case, the system is said to be stable, and in the second

case, it is said to be unstable.

To determine whether the two-rod system is stable or unstable,

we consider the forces acting on rod AC (Fig. 10.5). These forces

consist of two couples, namely the couple formed by P and P9, of

moment P(Ly2) sin Du, which tends to move the rod away from the

vertical, and the couple M exerted by the spring, which tends to

bring the rod back into its original vertical position. Since the angle

of deflection of the spring is 2 Du, the moment of the couple M is

M 5 K(2 Du). If the moment of the second couple is larger than the

moment of the first couple, the system tends to return to its original

equilibrium position; the system is stable. If the moment of the first

couple is larger than the moment of the second couple, the system

tends to move away from its original equilibrium position; the system

is unstable. The value of the load for which the two couples balance

each other is called the critical load and is denoted by P

. We

have

sin ¢u 5 K

2 ¢u

(10.1)

or, since sin ¢u < ¢u,

5 4K

L (10.2)

Clearly, the system is stable for P , P

, that is, for values of the load

smaller than the critical value, and unstable for P . P

Let us assume that a load P . P

has been applied to the

two rods of Fig. 10.3 and that the system has been disturbed. Since

P . P

, the system will move further away from the vertical and,

after some oscillations, will settle into a new equilibrium position

(Fig. 10.6a). Considering the equilibrium of the free body AC

(Fig. 10.6b), we obtain an equation similar to Eq. (10.1), but involv-

ing the finite angle u, namely

P1L

22 sin u 5 K12u2

sin u

(10.3)

The value of u corresponding to the equilibrium position rep-

resented in Fig. 10.6 is obtained by solving Eq. (10.3) by trial and

error. But we observe that, for any positive value of u, we have

sin u , u. Thus, Eq. (10.3) yields a value of u different from zero

only when the left-hand member of the equation is larger than one.

Recalling Eq. (10.2), we note that this is indeed the case here, since

we have assumed P . P

. But, if we had assumed P , P

, the second

equilibrium position shown in Fig. 10.6 would not exist and the only

(a)(b)













P P

Fig. 10.4

L/2





Fig. 10.5

L/2



(b)(a)

Fig. 10.6 Column model in buckled

position.

bee80288_ch10_630-691.indd Page 634 11/19/10 12:57:23 AM user-f499bee80288_ch10_630-691.indd Page 634 11/19/10 12:57:23 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

635

possible equilibrium position would be the position corresponding

to u 5 0. We thus check that, for P , P

, the position u 5 0 must

be stable.

This observation applies to structures and mechanical systems

in general, and will be used in the next section, where the stability

of elastic columns will be discussed.

10.3 EULER’S FORMULA FOR PIN-ENDED COLUMNS

Returning to the column AB considered in the preceding section

(Fig. 10.1), we propose to determine the critical value of the load P,

i.e., the value P

of the load for which the position shown in

Fig. 10.1 ceases to be stable. If P . P

, the slightest misalignment

or disturbance will cause the column to buckle, i.e., to assume a

curved shape as shown in Fig. 10.2.

Our approach will be to determine the conditions under which

the configuration of Fig. 10.2 is possible. Since a column can be

considered as a beam placed in a vertical position and subjected to

an axial load, we proceed as in Chap. 9 and denote by x the distance

from end A of the column to a given point Q of its elastic curve,

and by y the deflection of that point (Fig. 10.7a). It follows that the

x axis will be vertical and directed downward, and the y axis hori-

zontal and directed to the right. Considering the equilibrium of the

free body AQ (Fig. 10.7b), we find that the bending moment at Q is

M 5 2Py. Substituting this value for M in Eq. (9.4) of Sec. 9.3, we

write

(10.4)

or, transposing the last term,

y 5 0

(10.5)

This equation is a linear, homogeneous differential equation of the

second order with constant coefficients. Setting

(10.6)

we write Eq. (10.5) in the form

1 p

y 5 0

(10.7)

which is the same as that of the differential equation for simple

harmonic motion except, of course, that the independent variable

is now the distance x instead of the time t. The general solution of

Eq. (10.7) is

5 A sin px 1 B cos px (10.8)

as we easily check by computing d

yydx

and substituting for y and

yydx

into Eq. (10.7).

10.3 Euler’s Formula for Pin-Ended Columns

Fig. 10.1 Column

(repeated)

Fig. 10.2 Buckled

column (repeated)

[ x  0, y  0]

[ x  L, y  0]

(a)(b)

P P

Fig. 10.7 Column in buckled position.

bee80288_ch10_630-691.indd Page 635 11/19/10 12:57:30 AM user-f499bee80288_ch10_630-691.indd Page 635 11/19/10 12:57:30 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

636

Columns

Recalling the boundary conditions that must be satisfied at ends

A and B of the column (Fig. 10.7a), we first make x 5 0, y 5 0 in

Eq. (10.8) and find that B 5 0. Substituting next x 5 L, y 5 0, we

obtain

A sin pL 5 0 (10.9)

This equation is satisfied either if A 5 0, or if sin pL 5 0. If the

first of these conditions is satisfied, Eq. (10.8) reduces to y 5 0 and

the column is straight (Fig. 10.1). For the second condition to be

satisfied, we must have pL 5 np or, substituting for p from (10.6)

and solving for P,

P 5

(10.10)

The smallest of the values of P defined by Eq. (10.10) is that corre-

sponding to n 5 1. We thus have

(10.11)

The expression obtained is known as Euler’s formula, after the

Swiss mathematician Leonhard Euler (1707–1783). Substituting this

expression for P into Eq. (10.6) and the value obtained for p into

Eq. (10.8), and recalling that B 5 0, we write

5 A sin

(10.12)

which is the equation of the elastic curve after the column has buck-

led (Fig. 10.2). We note that the value of the maximum deflection,

5 A, is indeterminate. This is due to the fact that the differential

equation (10.5) is a linearized approximation of the actual governing

differential equation for the elastic curve.†

If P , P

, the condition sin pL 5 0 cannot be satisfied, and

the solution given by Eq. (10.12) does not exist. We must then have

A 5 0, and the only possible configuration for the column is a straight

one. Thus, for P , P

the straight configuration of Fig. 10.1 is

stable.

In the case of a column with a circular or square cross section,

the moment of inertia I of the cross section is the same about any

centroidal axis, and the column is as likely to buckle in one plane as

another, except for the restraints that can be imposed by the end

connections. For other shapes of cross section, the critical load

should be computed by making I 5 I

min

in Eq. (10.11); if buckling

occurs, it will take place in a plane perpendicular to the correspond-

ing principal axis of inertia.

The value of the stress corresponding to the critical load is

called the critical stress and is denoted by s

. Recalling Eq. (10.11)

†We recall that the equation d

yydx

5 M/EI was obtained in Sec. 9.3 by assuming that

the slope dyydx of the beam could be neglected and that the exact expression given in

Eq. (9.3) for the curvature of the beam could be replaced by 1yr 5 d

yydx

bee80288_ch10_630-691.indd Page 636 11/19/10 12:57:35 AM user-f499bee80288_ch10_630-691.indd Page 636 11/19/10 12:57:35 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10