Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.


Apago PDF Enhancer
587
SAMPLE PROBLEM 9.9
For the beam and loading shown, determine the reaction at the fixed support C.
SOLUTION
Principle of Superposition. Assuming the axial force in the beam to
be zero, the beam ABC is indeterminate to the second degree and we
choose two reaction components as redundant, namely, the vertical force
R
C
and the couple M
C
. The deformations caused by the given load P, the
force R
C
, and the couple M
C
will be considered separately as shown.
For each load, the slope and deflection at point C will be found by using
the table of Beam Deflections and Slopes in Appendix D.
Load P. We note that, for this loading, portion BC of the beam is
straight.
1u
C
2
P
5 1u
B
2
P
52
Pa
2
2E
I
1y
C
2
P
5 1y
B
2
P
1 1u
B
2
p
b
52
Pa
3
3EI
2
Pa
2
2EI
b 52
Pa
2
6EI
12a 1 3b2
Force R
C
1u
C
2
R
51
R
C
L
2
2E
I
1y
C
2
R
51
R
C
L
3
3
E
I
Couple M
C
1u
C
2
M
51
M
C
L
E
I
1y
C
2
M
51
M
C
L
2
2E
I
Boundary Conditions. At end C the slope and deflection must be zero:
3x 5 L, u
C
5 04: u
C
5
1
u
C
2
P
1
1
u
C
2
R
1
1
u
C
2
M
0 52
Pa
2
2EI
1
R
C
L
2
2EI
1
M
C
L
EI
(1)
3x 5 L, y
C
5 04: y
C
5 1y
C
2
P
1 1y
C
2
R
1 1y
C
2
M
0 52
Pa
2
6EI
12a 1 3b21
R
C
L
3
3EI
1
M
C
L
2
2EI
(2)
Reaction Components at C. Solving simultaneously Eqs. (1) and (2),
we find after reductions
R
C
51
Pa
2
L
3
1a 1 3b2
R
C
5
Pa
2
L
3
1a 1 3b2 x>
M
C
52
Pa
2
b
L
2
M
C
5
Pa
2
b
L
2
ib
Using the methods of statics, we can now determine the reaction at A.
B
P
C
C
a b
A
B
A
P
M
C
M
C
R
C
R
C
a b
C
C
L
A
C
C
A
A
L
BB
C
C
A
A
A
(
C
)
M
(y
C
)
M
(
C
)
P
(
C
)
R
(
B
)
P
(y
C
)
P
(y
C
)
R
(y
B
)
P
[
B
0]
[y
B
0]
L
a
b
R
A
R
C
Pa
2
b
L
2
M
C
P
Pab
2
L
2
M
A
Pb
2
L
3
R
A
(3a
b)
Pa
2
L
3
R
C
(a
3b)
B
P
C
L
a
b
A
bee80288_ch09_548-629.indd Page 587 11/18/10 8:57:20 PM user-f499bee80288_ch09_548-629.indd Page 587 11/18/10 8:57:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
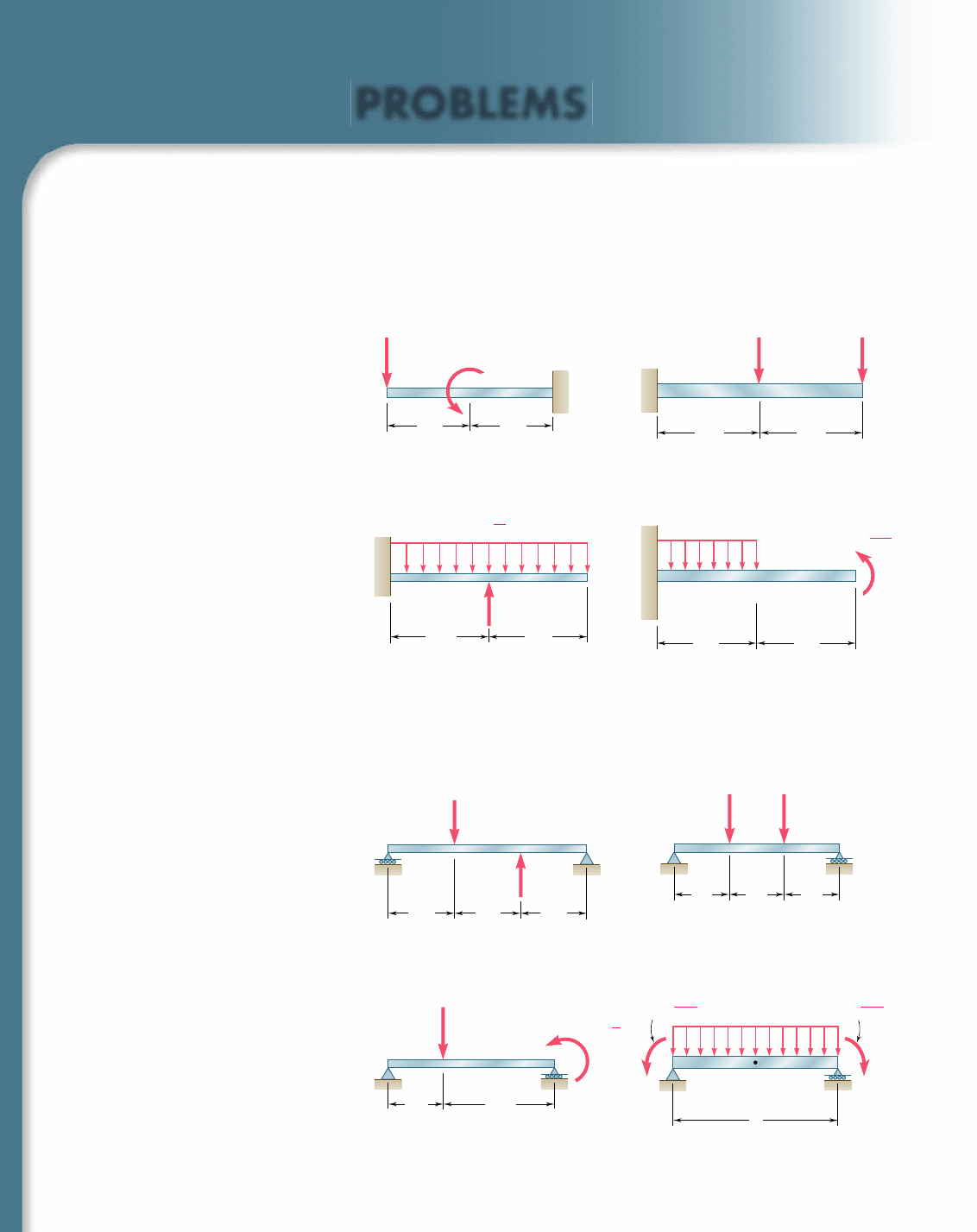
PROBLEMS
588
Use the method of superposition to solve the following
problems and assume that the flexural rigidity EI of each
beam is constant.
9.65 through 9.68 For the cantilever beam and loading shown,
determine the slope and deflection at the free end.
B
A
C
L/2 L/2
M PL
P
Fig. P9.65
Fig. P9.66
C
A B
L/2 L/2
P P
B
C
w
L/2 L/2
A
P
P
L
Fig. P9.67
CBA
w
wL
2
24
M
L/2 L/2
Fig. P9.68
9.69 through 9.72 For the beam and loading shown, determine
(a) the deflection at C, (b) the slope at end A.
D
C
B
P
P
A
L/3 L/3 L/3
Fig. P9.69
CB
A
D
L/3 L/3 L/3
P P
Fig. P9.70
B
C
P
A
L/32L/3
M
B
P
L
3
Fig. P9.71
B
w
A
wL
2
12
M
A
wL
2
12
M
B
C
L
Fig. P9.72
bee80288_ch09_548-629.indd Page 588 11/1/10 8:39:32 PM user-f499bee80288_ch09_548-629.indd Page 588 11/1/10 8:39:32 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
589
Problems
9.73 For the cantilever beam and loading shown, determine the slope
and deflection at end C. Use E 5 200 GPa.
3 kN
C
B
A
0.75 m 0.5 m
S100 11.5
3 kN
Fig. P9.73 and P9.74
9.74 For the cantilever beam and loading shown, determine the slope
and deflection at point B. Use E 5 200 GPa.
9.75 For the cantilever beam and loading shown, determine the slope
and deflection at end A. Use E 5 29 3 10
6
psi.
C
B
1 kip/ft
2 ft 3 ft
A
1 kip
2.0 in.
4.0 in.
Fig. P9.75 and P9.76
9.76 For the cantilever beam and loading shown, determine the slope
and deflection at point B. Use E 5 29 3 10
6
psi.
9.77 and 9.78 For the beam and loading shown, determine (a) the
slope at end A, (b) the deflection at point C. Use E 5 200 GPa.
B
C
140 kN
80 kN · m80 kN · m
2.5 m 2.5 m
A
W410 46.1
Fig. P9.77
1.3 m 2.6 m
B
C
8 kN/m
35 kN
A
W360 39
Fig. P9.78
9.79 and 9.80 For the uniform beam shown, determine the reaction
at each of the three supports.
A
B
C
L/2L/2
M
0
Fig. P9.79
A E
D
CB
L/2 L/2 L/2 L/2
P 2P
Fig. P9.80
bee80288_ch09_548-629.indd Page 589 11/18/10 8:57:28 PM user-f499bee80288_ch09_548-629.indd Page 589 11/18/10 8:57:28 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
590
Defl ection of Beams
9.81 and 9.82 For the uniform beam shown, determine (a) the
reaction at A, (b) the reaction at B.
9.83 and 9.84 For the beam shown, determine the reaction at B.
B
A
C
w
L/2 L/2
Fig. P9.81
a
A
M
0
C
L
B
Fig. P9.82
B
A
L
w
Fig. P9.83
B
A
C
L/2 L/2
M
0
Fig. P9.84
9.85 A central beam BD is joined at hinges to two cantilever beams AB
and DE. All beams have the cross section shown. For the loading
shown, determine the largest w so that the deflection at C does
not exceed 3 mm. Use E 5 200 GPa.
A
CB
0.4 m 0.4 m 0.4 m 0.4 m
HingeHinge
DE
24 mm
12 mm
w
Fig. P9.85
9.86 The two beams shown have the same cross section and are joined
by a hinge at C. For the loading shown, determine (a) the slope
at point A, (b) the deflection at point B. Use E 5 29 3 10
6
psi.
A
B
CB
12 in.12 in.
6 in.
Hinge
D
800 lb
1.25 in.
1.25 in.
Fig. P9.86
9.87 Beam CE rests on beam AB as shown. Knowing that a W10 3 30
rolled-steel shape is used for each beam, determine for the loading
shown the deflection at point D. Use E 5 29 3 10
6
psi.
W10 30
30 kips
D
C
A
E
B
2 ft 4 ft
12 ft
4 ft 2 ft
Fig. P9.87
bee80288_ch09_548-629.indd Page 590 10/30/10 11:23:03 PM user-f499bee80288_ch09_548-629.indd Page 590 10/30/10 11:23:03 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
591
Problems
9.88 Beam AC rests on the cantilever beam DE as shown. Knowing that
a W410 3 38.8 rolled-steel shape is used for each beam, determine
for the loading shown (a) the deflection at point B, (b) the deflec-
tion at point D. Use E 5 200 GPa.
9.89 Before the 2-kip/ft load is applied, a gap, d
0
5 0.8 in., exists
between the W16 3 40 beam and the support at C. Knowing that
E 5 29 3 10
6
psi, determine the reaction at each support after
the uniformly distributed load is applied.
E
2.2 m 2.2 m 2.2 m
B
A
C
D
30 kN/m
Fig. P9.88
2 kips/ft
B
A
W16 40
12 ft 12 ft
C
0
Fig. P9.89
9.90 The cantilever beam BC is attached to the steel cable AB as shown.
Knowing that the cable is initially taut, determine the tension in the
cable caused by the distributed load shown. Use E 5 200 GPa.
9.91 Before the load P was applied, a gap, d
0
5 0.5 mm, existed between
the cantilever beam AC and the support at B. Knowing that E 5
200 GPa, determine the magnitude of P for which the deflection
at C is 1 mm.
W410 46.1
6 m
A 255 mm
2
3 m
20 kN/m
C
B
A
Fig. P9.90
C
P
AB
0
60 mm
60 mm
0.5 m 0.2 m
Fig. P9.91
9.92 For the loading shown, knowing that beams AC and BD have the
same flexural rigidity, determine the reaction at B.
50 lb/in.
D
C
B
20 in.
20 in.
25 in.
A
Fig. P9.92
bee80288_ch09_548-629.indd Page 591 10/30/10 11:23:18 PM user-f499bee80288_ch09_548-629.indd Page 591 10/30/10 11:23:18 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
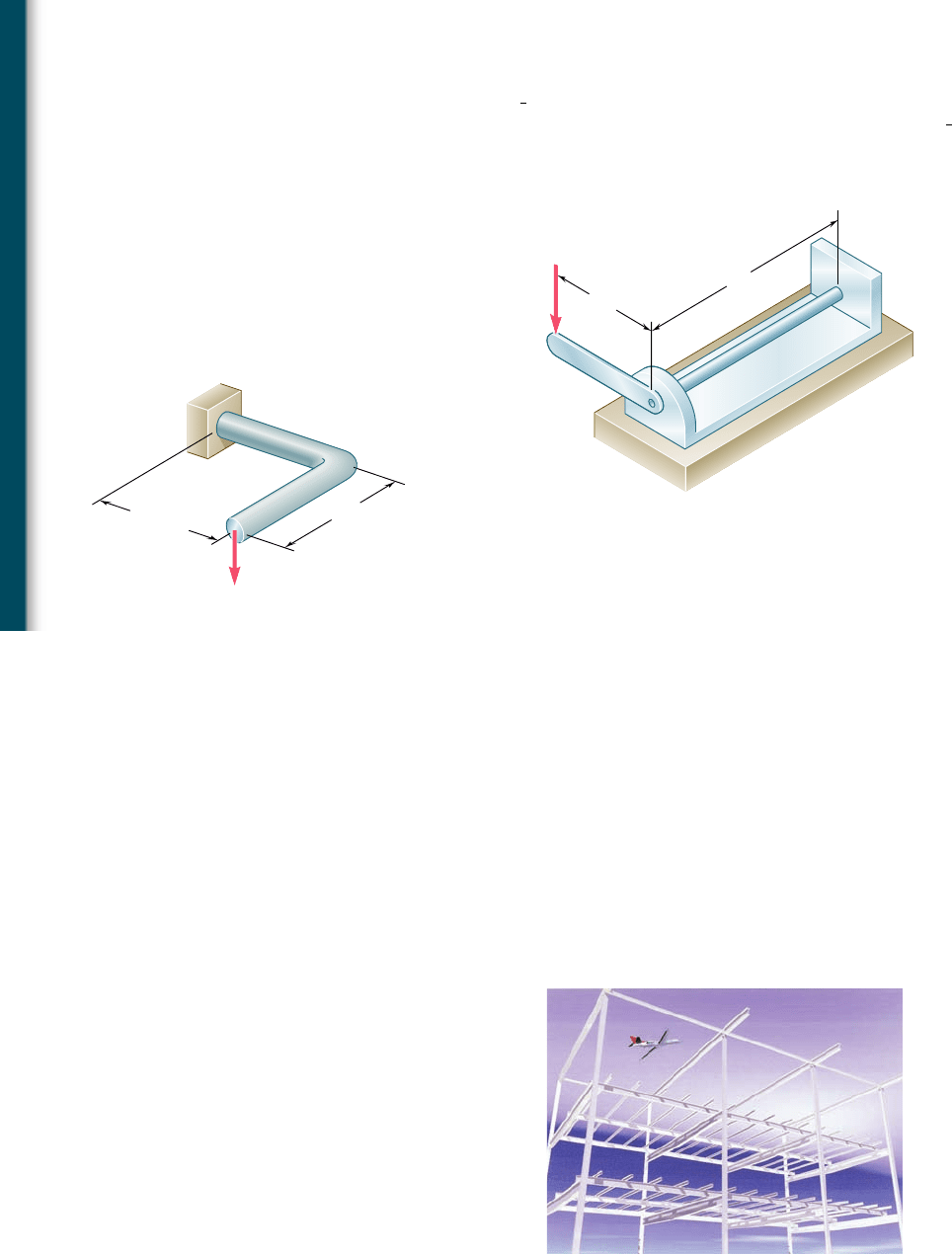
9.93 A
7
8
-in.-diameter rod BC is attached to the lever AB and to the
fixed support at C. Lever AB has a uniform cross section
3
8
in. thick
and 1 in. deep. For the loading shown, determine the deflection
of point A. Use E 5 29 3 10
6
psi and G 5 11.2 3 10
6
psi.
20 in.
C
B
80 lb
10 in.
A
Fig. P9.93
9.94 A 16-mm-diameter rod has been bent into the shape shown.
Determine the deflection of end C after the 200-N force is applied.
Use E 5 200 GPa and G 5 80 GPa.
L 250 mm
L 250 mm
200 N
B
C
A
Fig. P9.94
*9.9 MOMENT-AREA THEOREMS
In Sec. 9.2 through Sec. 9.6 we used a mathematical method based
on the integration of a differential equation to determine the deflec-
tion and slope of a beam at any given point. The bending moment
was expressed as a function M(x) of the distance x measured along
the beam, and two successive integrations led to the functions u(x)
and y(x) representing, respectively, the slope and deflection at any
point of the beam. In this section you will see how geometric proper-
ties of the elastic curve can be used to determine the deflection and
slope of a beam at a specific point (Photo 9.4).
Photo 9.4 The deflections of the beams
supporting the floors of a building should be
taken into account in the design process.
592
Defl ection of Beams
bee80288_ch09_548-629.indd Page 592 10/30/10 11:23:29 PM user-f499bee80288_ch09_548-629.indd Page 592 10/30/10 11:23:29 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09

Apago PDF Enhancer
593
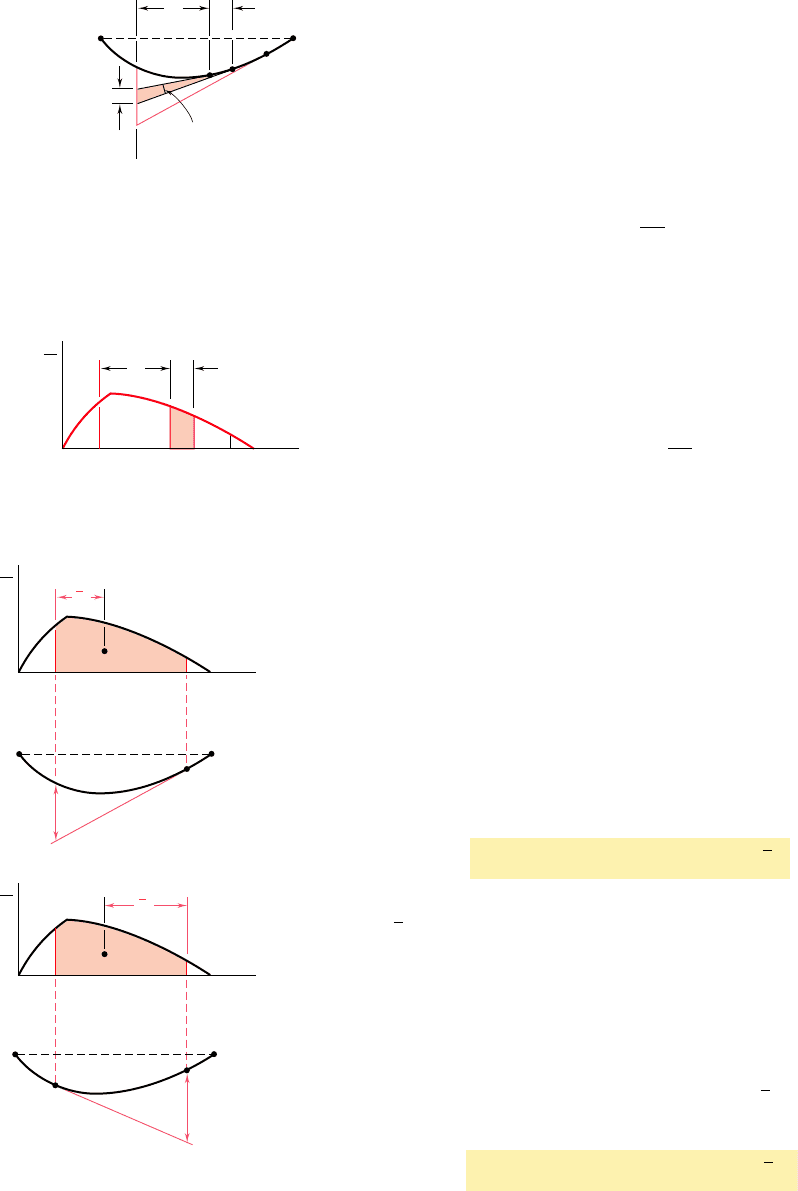
Consider a beam AB subjected to some arbitrary loading
(Fig. 9.37a). We draw the diagram representing the variation along
the beam of the quantity MyEI obtained by dividing the bending
moment M by the flexural rigidity EI (Fig. 9.37b). We note that,
except for a difference in the scales of ordinates, this diagram will
be the same as the bending-moment diagram if the flexural rigidity
of the beam is constant.
Recalling Eq. (9.4) of Sec. 9.3, and the fact that dyydx 5 u, we
write
d
u
dx
5
d
2
y
d
x
2
5
M
EI
or
du 5
M
E
I
dx
(9.54)†
Considering two arbitrary points C and D on the beam and
integrating both members of Eq. (9.54) from C to D, we write
#
u
D
u
C
du 5
#
x
D
x
C
M
EI
dx
or
u
D
2 u
C
5
#
x
D
x
C
M
EI
dx
(9.55)
where u
C
and u
D
denote the slope at C and D, respectively (Fig. 9.37c).
But the right-hand member of Eq. (9.55) represents the area under
the (MyEI) diagram between C and D, and the left-hand member the
angle between the tangents to the elastic curve at C and D (Fig. 9.37d).
Denoting this angle by u
DyC
, we have
u
DyC
5 area under (MyEI) diagram
between C and D
(9.56)
This is the first moment-area theorem.
We note that the angle u
DyC
and the area under the (M/EI)
diagram have the same sign. In other words, a positive area (i.e., an
area located above the x axis) corresponds to a counterclockwise
rotation of the tangent to the elastic curve as we move from C to D,
and a negative area corresponds to a clockwise rotation.
†This relation can also be derived without referring to the results obtained in Sec. 9.3, by
noting that the angle du formed by the tangents to the elastic curve at P and P9 is also
the angle formed by the corresponding normals to that curve (Fig. 9.38). We thus have
du 5 dsyr where ds is the length of the arc PP9 and r the radius of curvature at P. Sub-
stituting for 1yr from Eq. (4.21), and noting that, since the slope at P is very small, ds is
equal in first approximation to the horizontal distance dx between P and P9, we write
d
u 5
M
EI
dx
(9.54)
9.9 Moment-Area Theorems
B
B
B
C
C
C
D
D
D
A
A
A
M
EI
x
(a)
(b)
(c)
(d)
D
C
B
C
D
A
D/C
Fig. 9.37 First moment-area theorem.
d
d
C
ds
P'
P
Fig. 9.38
bee80288_ch09_548-629.indd Page 593 11/18/10 10:03:00 PM user-f499bee80288_ch09_548-629.indd Page 593 11/18/10 10:03:00 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
594
Defl ection of Beams
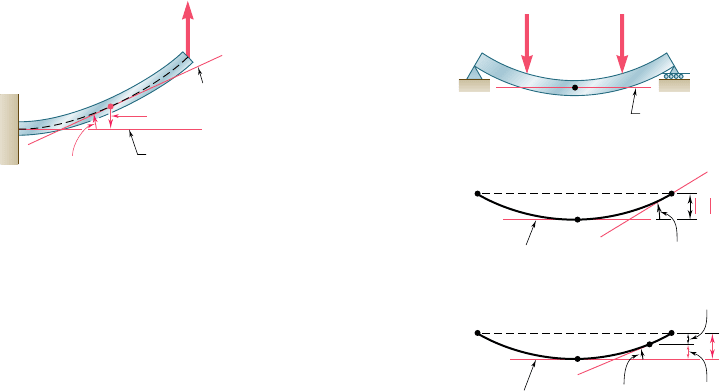
Let us now consider two points P and P9 located between C
and D, and at a distance dx from each other (Fig. 9.39). The tangents
to the elastic curve drawn at P and P9 intercept a segment of length
dt on the vertical through point C. Since the slope u at P and the
angle du formed by the tangents at P and P9 are both small quanti-
ties, we can assume that dt is equal to the arc of circle of radius x
1
subtending the angle du. We have, therefore,
dt 5 x
1
du
or, substituting for du from Eq. (9.54),
dt 5 x
1
M
E
I
dx
(9.57)
We now integrate Eq. (9.57) from C to D. We note that, as
point P describes the elastic curve from C to D, the tangent at P
sweeps the vertical through C from C to E. The integral of the left-
hand member is thus equal to the vertical distance from C to the
tangent at D. This distance is denoted by t
CyD
and is called the tan-
gential deviation of C with respect to D. We have, therefore,
t
C
y
D
5
#
x
D
x
C
x
1
M
EI
dx
(9.58)
We now observe that (MyEI) dx represents an element of area
under the (MyEI) diagram, and x
1
(MyEI) dx the first moment of that
element with respect to a vertical axis through C (Fig. 9.40). The
right-hand member in Eq. (9.58), thus, represents the first moment
with respect to that axis of the area located under the (MyEI) diagram
between C and D.
We can, therefore, state the second moment-area theorem as
follows: The tangential deviation t
CyD
of C with respect to D is equal
to the first moment with respect to a vertical axis through C of the
area under the (MyEI) diagram between C and D.
Recalling that the first moment of an area with respect to an
axis is equal to the product of the area and of the distance from its
centroid to that axis, we may also express the second moment-area
theorem as follows:
t
C
y
D
5
1
area between C and D
2
x
1
(9.59)
where the area refers to the area under the (MyEI) diagram, and
where
x
1
is the distance from the centroid of the area to the vertical
axis through C (Fig. 9.41a).
Care should be taken to distinguish between the tangential
deviation of C with respect to D, denoted by t
CyD
, and the tangential
deviation of D with respect to C, which is denoted by t
DyC
. The tan-
gential deviation t
DyC
represents the vertical distance from D to the
tangent to the elastic curve at C, and is obtained by multiplying the
area under the (MyEI) diagram by the distance
x
2
from its centroid
to the vertical axis through D (Fig. 9.41b):
t
D
y
C
5
1
area between C and D
2
x
2
(9.60)
BCDA
M
E
I
x
P'P
dx
x
1
Fig. 9.40
Fig. 9.41 Second moment-area theorem.
B
A
B
C
t
C/D
t
D/C
D
D
A
C'
D'
C
BCDA
M
EI
x
BCDA
M
E
I
x
x
2
(a)
(b)
x
1
B
C
D
dx
x
1
dt
d
A
P'
P
E
Fig. 9.39
bee80288_ch09_548-629.indd Page 594 10/30/10 11:23:40 PM user-f499bee80288_ch09_548-629.indd Page 594 10/30/10 11:23:40 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
595
We note that, if an area under the (MyEI) diagram is located
above the x axis, its first moment with respect to a vertical axis will
be positive; if it is located below the x axis, its first moment will be
negative. We check from Fig. 9.41, that a point with a positive tan-
gential deviation is located above the corresponding tangent, while
a point with a negative tangential deviation would be located below
that tangent.
*9.10 APPLICATION TO CANTILEVER BEAMS AND
BEAMS WITH SYMMETRIC LOADINGS
We recall that the first moment-area theorem derived in the preceding
section defines the angle u
DyC
between the tangents at two points C
and D of the elastic curve. Thus, the angle u
D
that the tangent at D
forms with the horizontal, i.e., the slope at D, can be obtained only
if the slope at C is known. Similarly, the second moment-area theo-
rem defines the vertical distance of one point of the elastic curve from
the tangent at another point. The tangential deviation t
DyC
, therefore,
will help us locate point D only if the tangent at C is known. We
conclude that the two moment-area theorems can be applied effec-
tively to the determination of slopes and deflections only if a certain
reference tangent to the elastic curve has first been determined.
In the case of a cantilever beam (Fig. 9.42), the tangent to the
elastic curve at the fixed end A is known and can be used as the ref-
erence tangent. Since u
A
5 0, the slope of the beam at any point D
is u
D
5 u
DyA
and can be obtained by the first moment-area theorem.
On the other hand, the deflection y
D
of point D is equal to the tan-
gential deviation t
DyA
measured from the horizontal reference tangent
at A and can be obtained by the second moment-area theorem.
D
=
D/A
y
D
= t
D/A
Reference tangent
Tangent at D
D
A
P
Fig. 9.42 Application of moment-area
method to cantilever beams.
9.10 Application to Cantilever Beams and
Beams with Symmetric Loadings
C
C
B
y
max
t
B/C
A
B
A
P
Horizontal
Reference tangent
(a)
(b)
B/CB
C
B
D
t
D/C
t
B/C
y
D
A
Reference tangent
(c)
D/CD
P
Fig. 9.43 Application of moment-area
method to simply supported beams with
symmetric loadings.
In the case of a simply supported beam AB with a symmetric
loading (Fig. 9.43a) or in the case of an overhanging symmetric beam
with a symmetric loading (see Sample Prob. 9.11), the tangent at the
center C of the beam must be horizontal by reason of symmetry and
can be used as the reference tangent (Fig. 9.43b). Since u
C
5 0, the
slope at the support B is u
B
5 u
ByC
and can be obtained by the first
moment-area theorem. We also note that |y|
max
is equal to the tan-
gential deviation t
ByC
and can, therefore, be obtained by the second
moment-area theorem. The slope at any other point D of the beam
(Fig. 9.43c) is found in a similar fashion, and the deflection at D can
be expressed as y
D
5 t
DyC
2 t
ByC
.
bee80288_ch09_548-629.indd Page 595 10/30/10 11:23:47 PM user-f499bee80288_ch09_548-629.indd Page 595 10/30/10 11:23:47 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
Apago PDF Enhancer
596
EXAMPLE 9.09
Determine the slope and deflection at end B of the prismatic cantilever
beam AB when it is loaded as shown (Fig. 9.44), knowing that the flexural
rigidity of the beam is EI 5 10 MN ? m
2
.
We first draw the free-body diagram of the beam (Fig. 9.45a).
Summing vertical components and moments about A, we find that the
reaction at the fixed end A consists of a 50 kN upward vertical force R
A
and a 60 kN ? m counterclockwise couple M
A
. Next, we draw the
bending-moment diagram (Fig. 9.45b) and determine from similar tri-
angles the distance x
D
from the end A to the point D of the beam where
M 5 0:
x
D
60
5
3
2 x
D
90
5
3
150
x
D
5
1
.
2
m
Dividing by the flexural rigidity EI the values obtained for M, we
draw the (MyEI) diagram (Fig. 9.46) and compute the areas correspond-
ing respectively to the segments AD and DB, assigning a positive sign to
the area located above the x axis, and a negative sign to the area located
below that axis. Using the first moment-area theorem, we write
u
B
y
A
5 u
B
2 u
A
5 area
f
rom A to B 5 A
1
1 A
2
52
1
2
1
1.2 m
21
6 3 10
23
m
21
2
1
1
2
1
1.8 m
21
9 3 10
23
m
21
2
523
.
6 3 10
2
3
1 8
.
1 3 10
2
3
514.5 3 10
2
3
rad
and, since u
A
5 0,
u
B
514.5 3 10
2
3
rad
Using now the second moment-area theorem, we write that the
tangential deviation t
ByA
is equal to the first moment about a vertical axis
through B of the total area between A and B. Expressing the moment of
each partial area as the product of that area and of the distance from its
centroid to the axis through B, we have
t
B
y
A
5 A
1
1
2.6 m
2
1 A
2
1
0.6 m
2
5
1
23.6 3 10
2
3
21
2.6 m
2
1
1
8.1 3 10
2
3
21
0.6 m
2
529
.
36 mm 1 4
.
86 mm 524
.
50 mm
Since the reference tangent at A is horizontal, the deflection at B is equal
to t
ByA
and we have
y
B
5 t
B
y
A
524.50 mm
The deflected beam has been sketched in Fig. 9.47.
3 m
A
B
50 kN
90 kN · m
Fig. 9.44
60 kN · m
A
B
(a)
(b)
3 m x
D
x
D
M
A
60 kN · m
R
A
50 kN
90 kN · m
90 kN · m
M
A
BD
x
50 kN
Fig. 9.45
0.8 m
1.8 m
2.6 m
0.6 m
9 10
3
m
1
6 10
3
m
1
A
A
1
A
2
B
D
x
M
EI
1.2 m
Fig. 9.46
B
A
Reference tangent
B
B/A
4.5 10
–3
rad
y
B
t
B/A
4.5 mm
Fig. 9.47
bee80288_ch09_548-629.indd Page 596 11/18/10 8:57:43 PM user-f499bee80288_ch09_548-629.indd Page 596 11/18/10 8:57:43 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch09
