Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

267

Problems

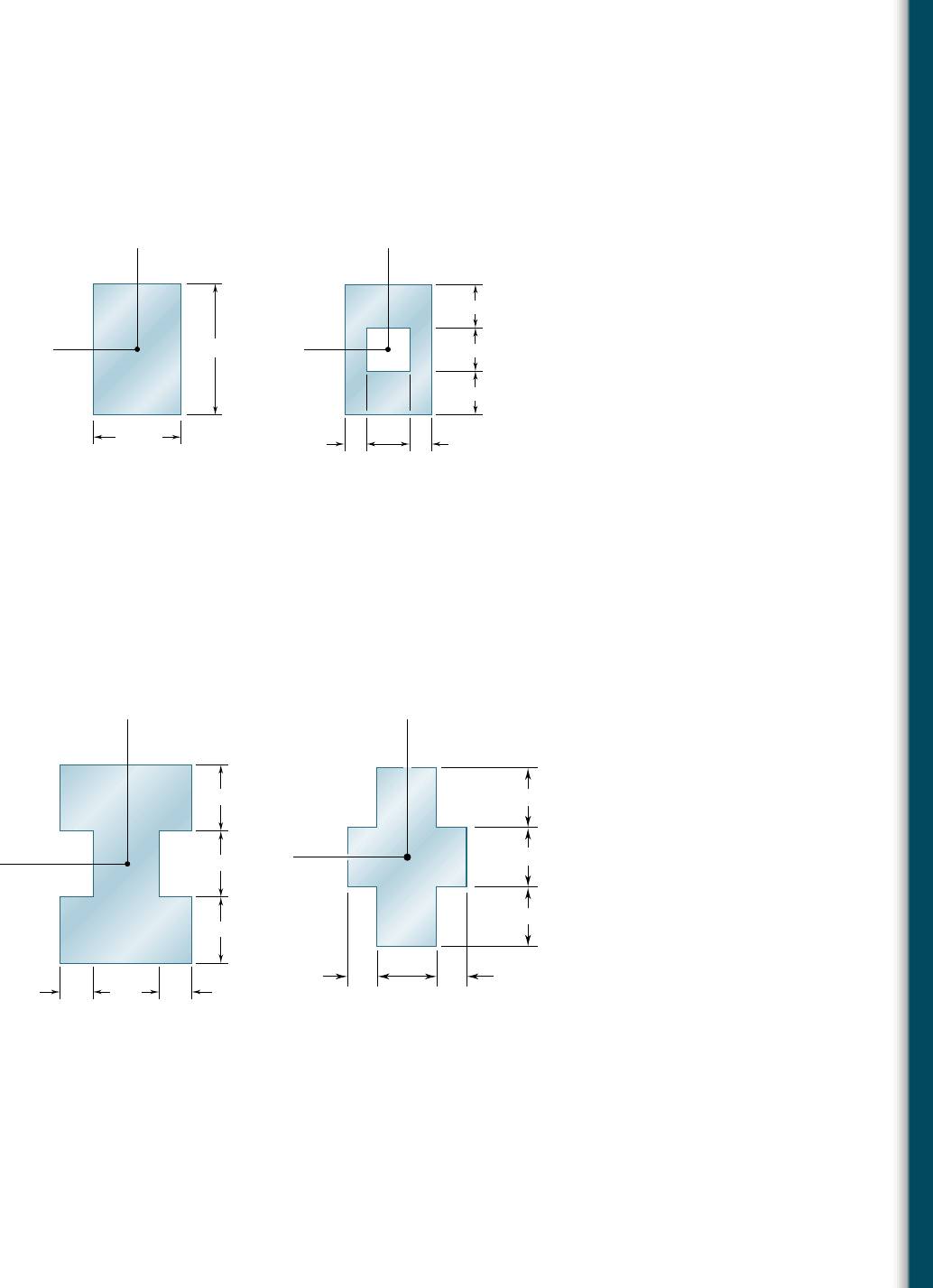
4.73 and 4.74 A beam of the cross section shown is made of a steel

that is assumed to be elastoplastic with E 5 200 GPa and s

240 MPa. For bending about the z axis, determine the bending

moment at which (a) yield first occurs, (b) the plastic zones at the

top and bottom of the bar are 30 mm thick.

90 mm

60 mm

Fig. P4.73

30 mm

15 mm15 mm

Fig. P4.74

4.75 and 4.76 A beam of the cross section shown is made of a steel

that is assumed to be elastoplastic with E 5 29 3 10

psi and

5 42 ksi. For bending about the z axis, determine the bending

moment at which (a) yield first occurs, (b) the plastic zones at the

top and bottom of the bar are 3 in. thick.

3 in.

3 in.1.5 in. 1.5 in.

Fig. P4.75

3 in.

1.5 in. 1.5 in.

Fig. P4.76

4.77 through 4.80 For the beam indicated, determine (a) the plastic

moment M

, (b) the shape factor of the cross section.

4.77 Beam of Prob. 4.73.

4.78 Beam of Prob. 4.74.

4.79 Beam of Prob. 4.75.

4.80 Beam of Prob. 4.76.

bee80288_ch04_220-313.indd Page 267 10/27/10 5:46:20 PM user-f499bee80288_ch04_220-313.indd Page 267 10/27/10 5:46:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

268

Pure Bending

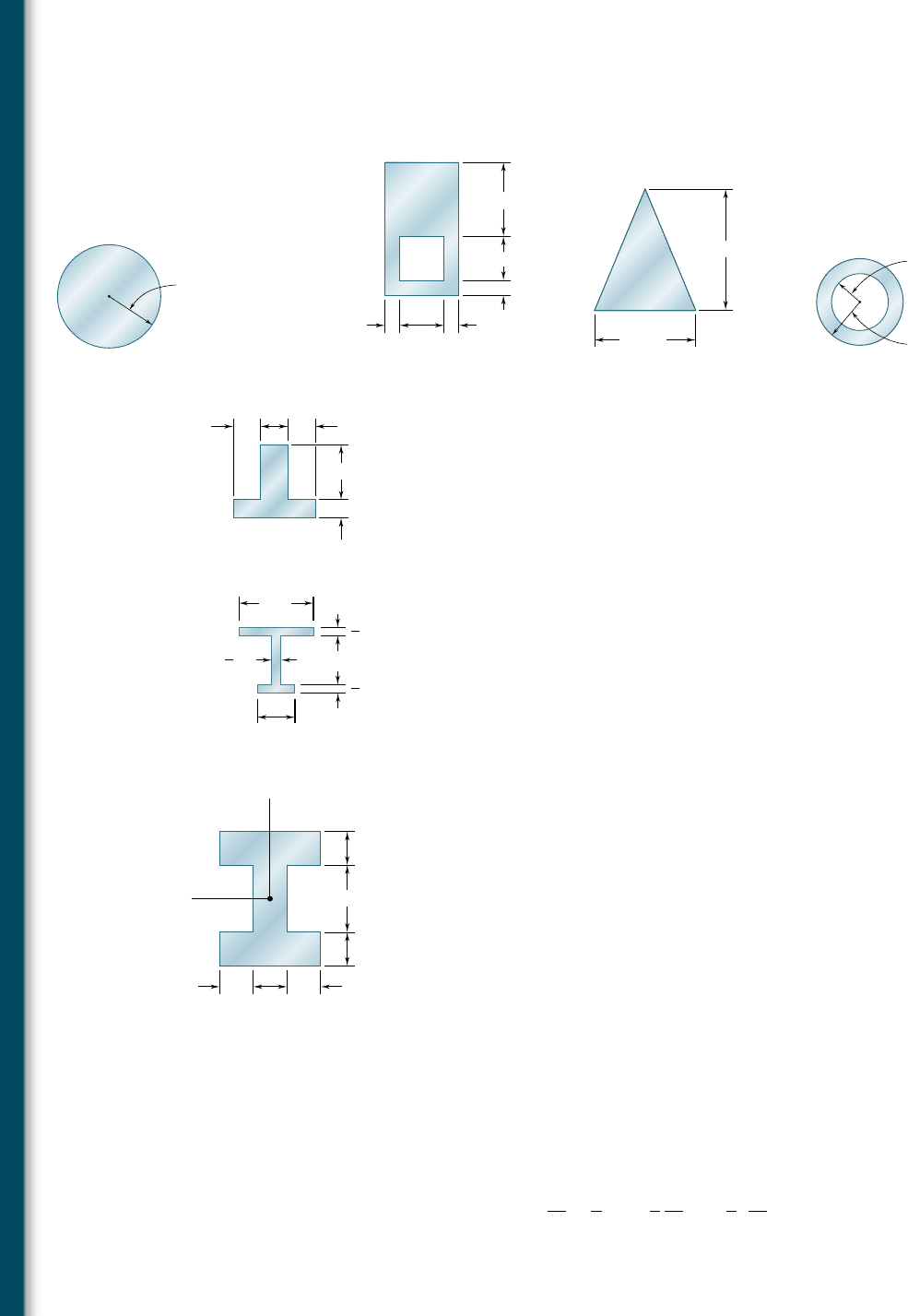
4.81 through 4.84 Determine the plastic moment M

of a steel

beam of the cross section shown, assuming the steel to be elasto-

plastic with a yield strength of 240 MPa.



18 mm

Fig. P4.81

50 mm

30 mm

10 mm

30 mm

10 mm10 mm

Fig. P4.82

36 mm

30 mm

Fig. P4.83

40 mm

60 mm

Fig. P4.84

4.85 and 4.86 Determine the plastic moment M

of the cross sec-

tion shown, assuming the steel to be elastoplastic with a yield

strength of 36 ksi.

4.87 and 4.88 For the beam indicated, a couple of moment equal to

the full plastic moment M

is applied and then removed. Using a yield

strength of 240 MPa, determine the residual stress at y 5 45 mm.

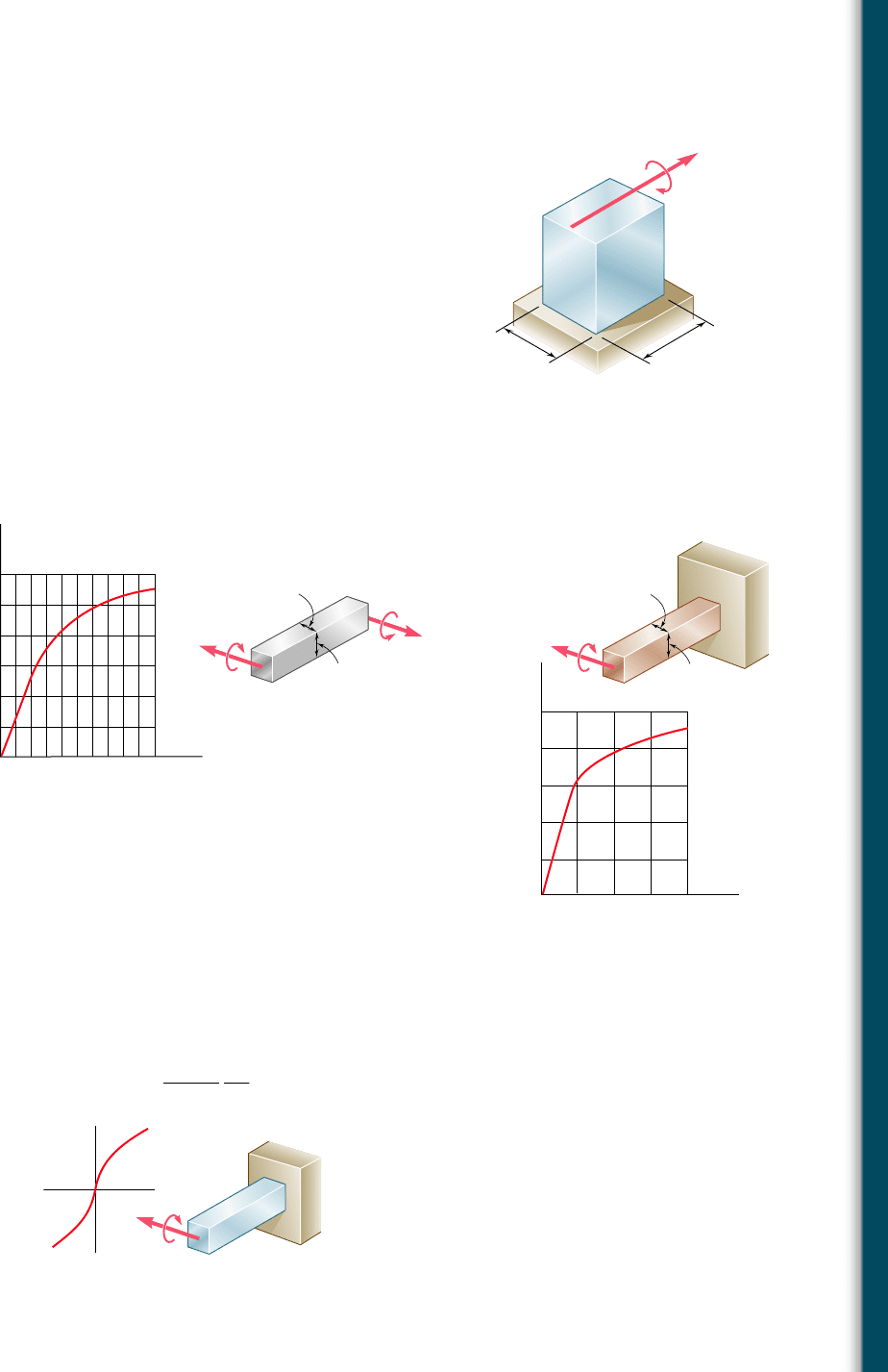
4.87 Beam of Prob. 4.73.

4.88 Beam of Prob. 4.74.

4.89 and 4.90 A bending couple is applied to the bar indicated,

causing plastic zones 3 in. thick to develop at the top and bottom

of the bar. After the couple has been removed, determine (a) the

residual stress at y 5 4.5 in., (b) the points where the residual

stress is zero, (c) the radius of curvature corresponding to the per-

manent deformation of the bar.

4.89 Beam of Prob. 4.75.

4.90 Beam of Prob. 4.76.

4.91 A bending couple is applied to the beam of Prob. 4.73, causing

plastic zones 30 mm thick to develop at the top and bottom of the

beam. After the couple has been removed, determine (a) the resid-

ual stress at y 5 45 mm, (b) the points where the residual stress

is zero, (c) the radius of curvature corresponding to the permanent

deformation of the beam.

4.92 A beam of the cross section shown is made of a steel that is assumed

to be elastoplastic with E 5 29 3 10

psi and s

5 42 ksi. A bend-

ing couple is applied to the beam about the z axis, causing plastic

zones 2 in. thick to develop at the top and bottom of the beam.

After the couple has been removed, determine (a) the residual

stress at y 5 2 in., (b) the points where the residual stress is zero,

mation of the beam.

4.93 A rectangular bar that is straight and unstressed is bent into an arc

of circle of radius r by two couples of moment M. After the couples

are removed, it is observed that the radius of curvature of the bar is

. Denoting by r

the radius of curvature of the bar at the onset of

yield, show that the radii of curvature satisfy the following relation:

e1 2

c1 2

0.6 in.0.6 in.

0.6 in.

1.2 in.

0.4 in.

Fig. P4.85

1 in.

2 in.

Fig. P4.92

2 in.

4 in.

3 in.

in.

Fig. P4.86

bee80288_ch04_220-313.indd Page 268 10/27/10 5:46:22 PM user-f499bee80288_ch04_220-313.indd Page 268 10/27/10 5:46:22 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

269

Problems

4.94 A solid bar of rectangular cross section is made of a material that

is assumed to be elastoplastic. Denoting by M

and r

, respectively,

the bending moment and radius of curvature at the onset of yield,

determine (a) the radius of curvature when a couple of moment

M 5 1.25 M

is applied to the bar, (b) the radius of curvature after

the couple is removed. Check the results obtained by using the

relation derived in Prob. 4.93.

4.95 The prismatic bar AB is made of a steel that is assumed to be

elastoplastic and for which E 5 200 GPa. Knowing that the radius

of curvature of the bar is 2.4 m when a couple of moment M 5

350 N ? m is applied as shown, determine (a) the yield strength of

the steel, (b) the thickness of the elastic core of the bar.

4.96 The prismatic bar AB is made of an aluminum alloy for which the

tensile stress-strain diagram is as shown. Assuming that the s-P dia-

gram is the same in compression as in tension, determine (a) the

radius of curvature of the bar when the maximum stress is 250 MPa,

(b) the corresponding value of the bending moment. (Hint: For part b,

plot s versus y and use an approximate method of integration.)

16 mm

20 mm

Fig. P4.95

60 mm

40 mm





(MPa)

300

200

100

0 0.005 0.010

Fig. P4.96

4.97 The prismatic bar AB is made of a bronze alloy for which the ten-

sile stress-strain diagram is as shown. Assuming that the s-P dia-

gram is the same in compression as in tension, determine (a) the

maximum stress in the bar when the radius of curvature of the bar

is 100 in., (b) the corresponding value of the bending moment.

(See hint given in Prob. 4.96.)

4.98 A prismatic bar of rectangular cross section is made of an alloy for

which the stress-strain diagram can be represented by the relation

P 5 ks

for s . 0 and P 5 2|ks

| for s , 0. If a couple M is

applied to the bar, show that the maximum stress is

1.2 in.

0.8 in.





(ksi)

0.004 0.008

Fig. P4.97





Fig. P4.98

bee80288_ch04_220-313.indd Page 269 10/26/10 4:30:32 PM user-f499bee80288_ch04_220-313.indd Page 269 10/26/10 4:30:32 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

270

Pure Bending

4.12 ECCENTRIC AXIAL LOADING IN A PLANE

OF SYMMETRY

We saw in Sec. 1.5 that the distribution of stresses in the cross sec-

tion of a member under axial loading can be assumed uniform only

if the line of action of the loads P and P9 passes through the centroid

of the cross section. Such a loading is said to be centric. Let us now

analyze the distribution of stresses when the line of action of the

loads does not pass through the centroid of the cross section, i.e.,

when the loading is eccentric.

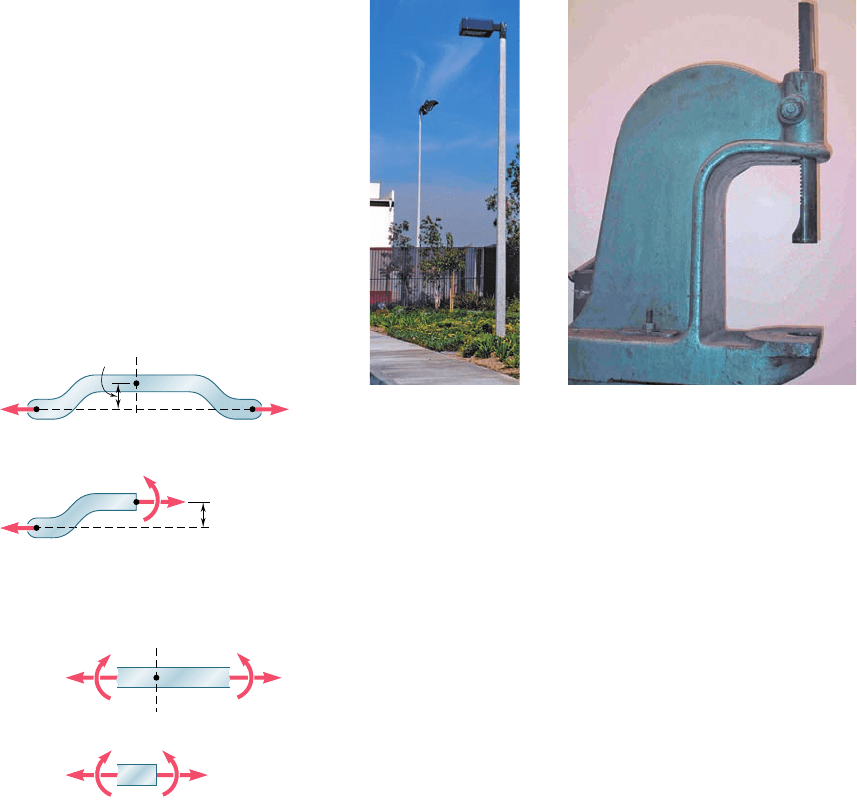
Two examples of an eccentric loading are shown in Photos 4.5 and

4.6. In the case of the walkway light, the weight of the lamp causes an

eccentric loading on the post. Likewise, the vertical forces exerted on

the press cause an eccentric loading on the back column of the press.

Photo 4.5

Photo 4.6

In this section, our analysis will be limited to members that

possess a plane of symmetry, and it will be assumed that the loads

are applied in the plane of symmetry of the member (Fig. 4.42a). The

internal forces acting on a given cross section may then be repre-

sented by a force F applied at the centroid C of the section and a

couple M acting in the plane of symmetry of the member (Fig. 4.42b).

The conditions of equilibrium of the free body AC require that the

force F be equal and opposite to P9 and that the moment of the

couple M be equal and opposite to the moment of P9 about C. Denot-

ing by d the distance from the centroid C to the line of action AB of

the forces P and P9, we have

F 5 P and M 5 Pd (4.49)

We now observe that the internal forces in the section would

have been represented by the same force and couple if the straight

portion DE of member AB had been detached from AB and sub-

jected simultaneously to the centric loads P and P9 and to the bend-

ing couples M and M9 (Fig. 4.43). Thus, the stress distribution due

PP'

(a)

(b)

Fig. 4.42 Member with eccentric

(a)

F  P

(b)

Fig. 4.43 Internal forces in

member with eccentric loading.

bee80288_ch04_220-313.indd Page 270 10/26/10 4:30:40 PM user-f499bee80288_ch04_220-313.indd Page 270 10/26/10 4:30:40 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

271

to the original eccentric loading can be obtained by superposing the

uniform stress distribution corresponding to the centric loads P and P9

and the linear distribution corresponding to the bending couples M

and M9 (Fig. 4.44). We write

5 1s

centric

1 1s

bending

yyy



Fig. 4.44 Stress distribution—eccentric loading.

or, recalling Eqs. (1.5) and (4.16):

(4.50)

where A is the area of the cross section and I its centroidal moment

of inertia, and where y is measured from the centroidal axis of the

cross section. The relation obtained shows that the distribution of

stresses across the section is linear but not uniform. Depending upon

the geometry of the cross section and the eccentricity of the load,

the combined stresses may all have the same sign, as shown in

Fig. 4.44, or some may be positive and others negative, as shown in

Fig. 4.45. In the latter case, there will be a line in the section, along

which s

5 0. This line represents the neutral axis of the section.

We note that the neutral axis does not coincide with the centroidal

axis of the section, since s

Z 0 for y 5 0.



N.A.



Fig. 4.45 Alternative stress distribution—eccentric loading.

The results obtained are valid only to the extent that the con-

ditions of applicability of the superposition principle (Sec. 2.12)

and of Saint-Venant’s principle (Sec. 2.17) are met. This means that

the stresses involved must not exceed the proportional limit of the

material, that the deformations due to bending must not apprecia-

bly affect the distance d in Fig. 4.42a, and that the cross section

where the stresses are computed must not be too close to points

D or E in the same figure. The first of these requirements clearly

shows that the superposition method cannot be applied to plastic

deformations.

4.12 Eccentric Axial Loading in a Plane

of Symmetry

bee80288_ch04_220-313.indd Page 271 10/26/10 4:30:46 PM user-f499bee80288_ch04_220-313.indd Page 271 10/26/10 4:30:46 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

272

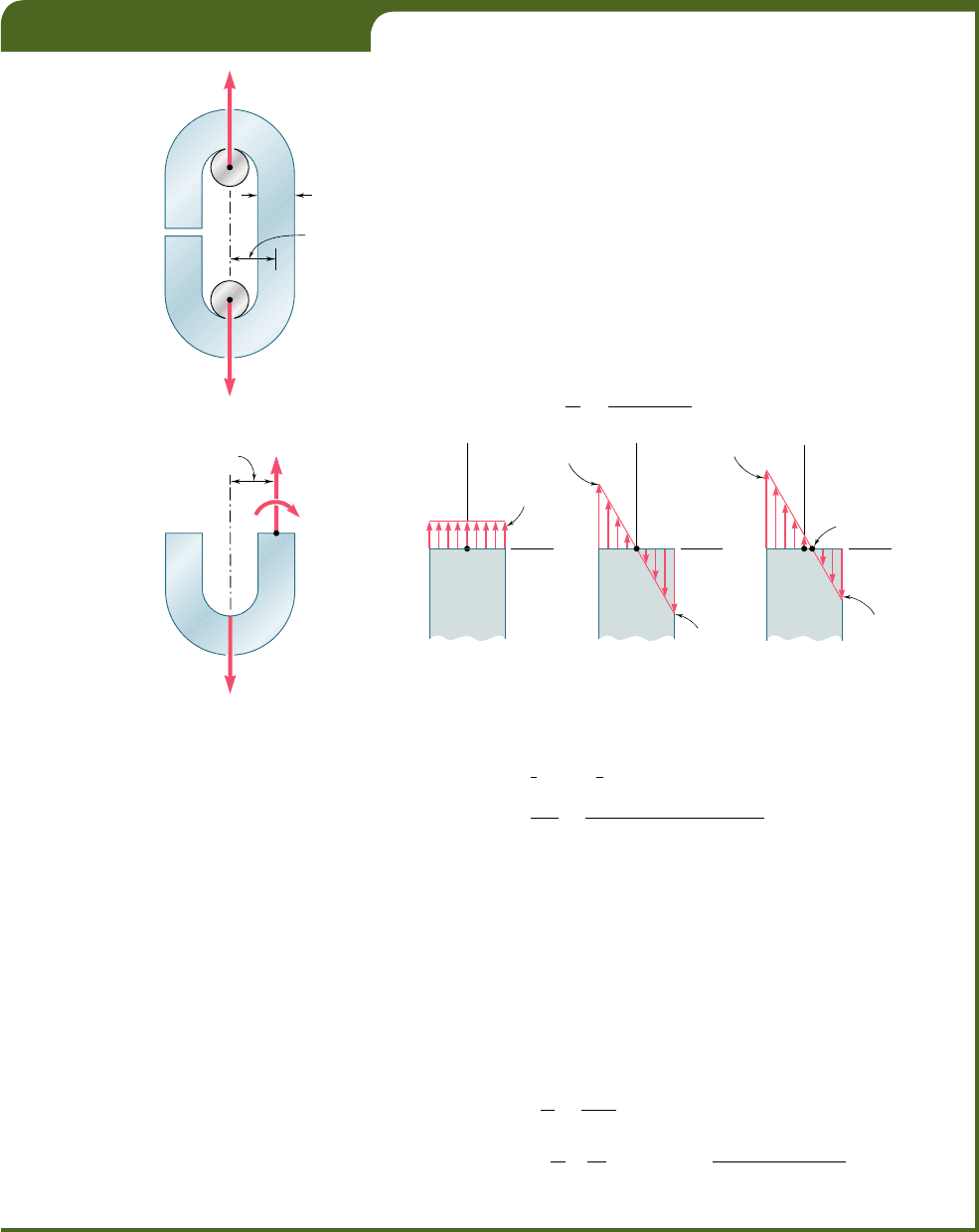
An open-link chain is obtained by bending low-carbon steel rods of 0.5-in.

diameter into the shape shown (Fig. 4.46). Knowing that the chain carries

a load of 160 lb, determine (a) the largest tensile and compressive stresses

in the straight portion of a link, (b) the distance between the centroidal

and the neutral axis of a cross section.

(a) Largest Tensile and Compressive Stresses. The internal

forces in the cross section are equivalent to a centric force P and a bend-

ing couple M (Fig. 4.47) of magnitudes

P 5 160 l

M 5 Pd 5 1160 lb210.65 in.25 104 lb ? in.

The corresponding stress distributions are shown in parts a and b of Fig. 4.48.

The distribution due to the centric force P is uniform and equal to s

PyA. We have

A 5 pc

5 p10.25 in.2

5 0.1963 in

160 lb

1963 in

5 815 psi

EXAMPLE 4.07

160 lb

0.5 in.

0.65 in.

Fig. 4.46

8475 psi

– 8475 psi

– 7660 psi

N.A.

815 psi

9290 psi



(a)(b)(c)

Fig. 4.48

160 lb

 0.65 in.

Fig. 4.47

The distribution due to the bending couple M is linear with a maximum

stress s

5 McyI. We write

I 5

p10.25 in.2

5 3.068 3 10

1104 lb ? in.210.25 in.

068 3 10

5 8475 psi

Superposing the two distributions, we obtain the stress distribution cor-

responding to the given eccentric loading (Fig. 4.48c). The largest tensile

and compressive stresses in the section are found to be, respectively,

5 s

1 s

5 815 1 8475 5 9290 psi

5 s

2 s

5 815 2 8475 527660 psi

(b) Distance Between Centroidal and Neutral Axes. The dis-

tance y

from the centroidal to the neutral axis of the section is obtained

by setting s

5 0 in Eq. (4.50) and solving for y

0 5

5 1815 psi2

3.068 3 10

104 lb ? in.

0240

in.

bee80288_ch04_220-313.indd Page 272 11/11/10 3:03:16 PM user-f499bee80288_ch04_220-313.indd Page 272 11/11/10 3:03:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

273

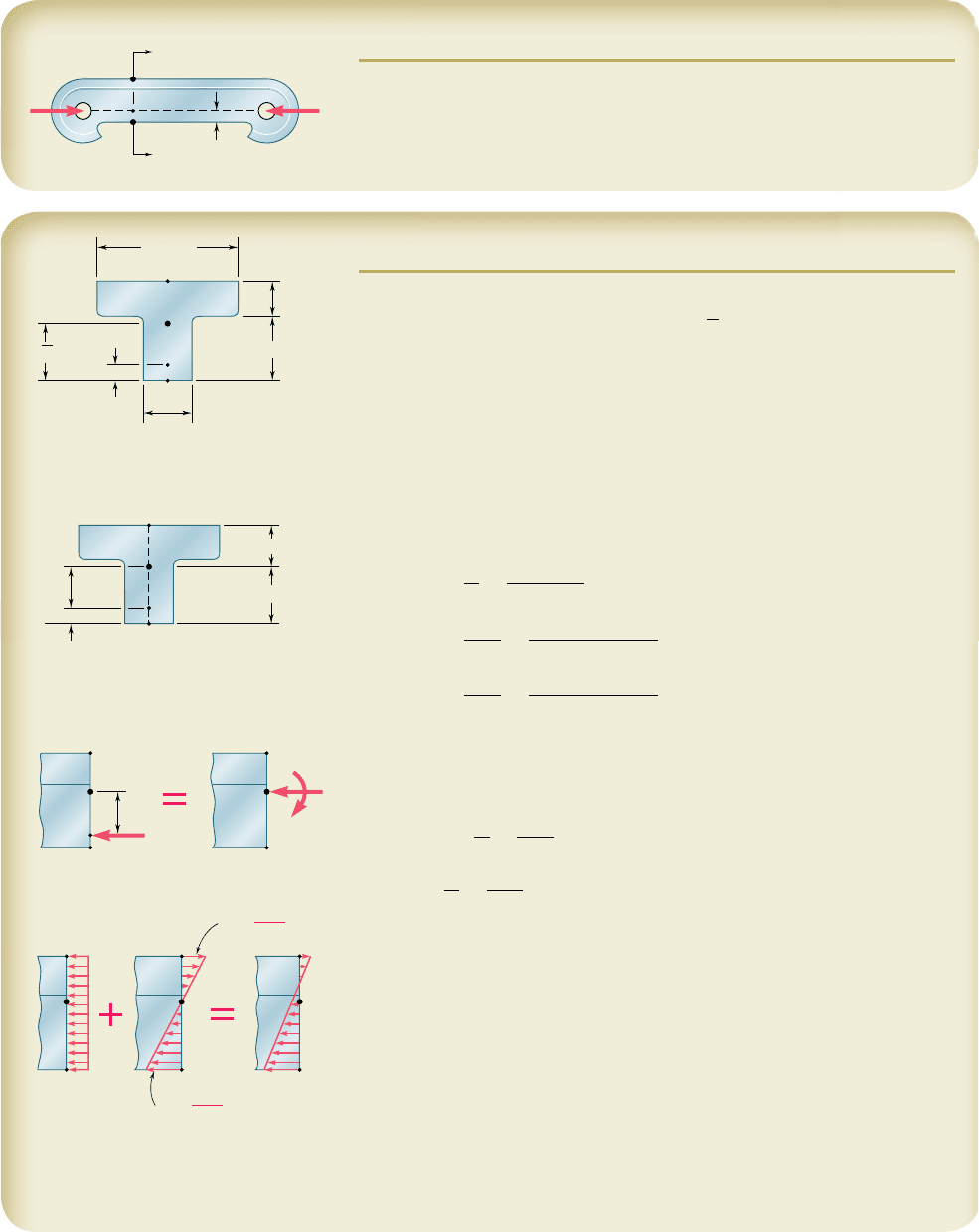
SAMPLE PROBLEM 4.8

Knowing that for the cast iron link shown the allowable stresses are 30 MPa

in tension and 120 MPa in compression, determine the largest force P which

can be applied to the link. (Note: The T-shaped cross section of the link has

previously been considered in Sample Prob. 4.2.)

10 mm

SOLUTION

Properties of Cross Section. From Sample Prob. 4.2, we have

5 3000 mm

5 3 3 10

Y 5 38 mm 5 0.038 m

I 5 868 3 10

We now write: d 5 (0.038 m) 2 (0.010 m) 5 0.028 m

Force and Couple at C. We replace P by an equivalent force-couple

system at the centroid C.

P 5 P M 5 P(d) 5 P(0.028 m) 5 0.028P

The force P acting at the centroid causes a uniform stress distribution (Fig. 1).

The bending couple M causes a linear stress distribution (Fig. 2).

3 3 10

5 333P1Compression2

10.028P210.022

868 3 10

5 710P1Tension2

10.028P210.038

868

5 1226P1Compression2

Superposition. The total stress distribution (Fig. 3) is found by super-

posing the stress distributions caused by the centric force P and by the

couple M. Since tension is positive, and compression negative, we have

52333P 1 710P 51377P1Tension2

52333P 2 1226P 521559P1Compression2

Largest Allowable Force. The magnitude of P for which the tensile

stress at point A is equal to the allowable tensile stress of 30 MPa is found

by writing

5 377P 5 30 MPa

79.6

◀

We also determine the magnitude of P for which the stress at B is equal to

the allowable compressive stress of 120 MPa.

521559P 52120 MPa

77.0

◀

The magnitude of the largest force P that can be applied without exceeding ei-

ther of the allowable stresses is the smaller of the two values we have found.

77.0

◀

90 mm

20 mm

40 mm

10 mm

30 mm

Section a–a



 0.022 m

 0.038 m

0.010 m









(1)

(2) (3)

bee80288_ch04_220-313.indd Page 273 11/11/10 3:03:17 PM user-f499bee80288_ch04_220-313.indd Page 273 11/11/10 3:03:17 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

PROBLEMS

274

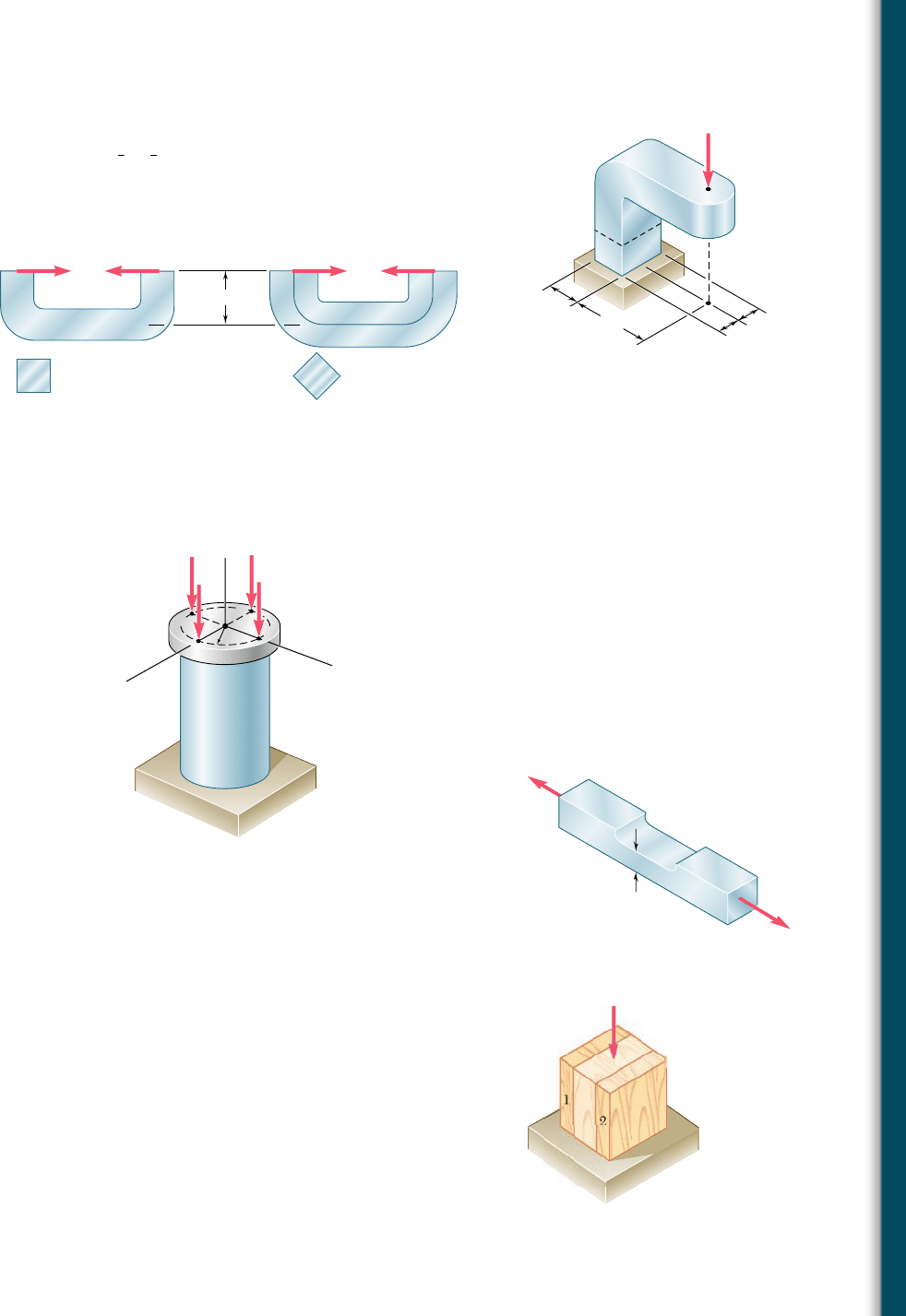
4.99 A short wooden post supports a 6-kip axial load as shown. Determine

the stress at point A when (a) b 5 0, (b) b 5 1.5 in., (c) b 5 3 in.

4.100 As many as three axial loads each of magnitude P 5 10 kips can

be applied to the end of a W8 3 21 rolled-steel shape. Determine

the stress at point A, (a) for the loading shown, (b) if loads are

applied at points 1 and 2 only.

z x

6 kips

3 in.

Fig. P4.99

3.5 in.

Fig. P4.100

4.101 Knowing that the magnitude of the horizontal force P is 8 kN,

determine the stress at (a) point A, (b) point B.

4.102 The vertical portion of the press shown consists of a rectangular

tube of wall thickness t 5 10 mm. Knowing that the press has been

tightened on wooden planks being glued together until P 5 20 kN,

determine the stress at (a) point A, (b) point B.

45 mm

30 mm

24 mm

15 mm

Fig. P4.101

80 mm

60 mm

Section a-a

200 mm

80 mm

Fig. P4.102

4.103 Solve Prob. 4.102, assuming that t 5 8 mm.

4.104 Determine the stress at points A and B, (a) for the loading shown,

(b) if the 60-kN loads are applied at points 1 and 2 only.

60 kN

150 mm

60 kN

150 mm

90 mm

120 mm

Fig. P4.104

bee80288_ch04_220-313.indd Page 274 10/26/10 4:31:12 PM user-f499bee80288_ch04_220-313.indd Page 274 10/26/10 4:31:12 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

275

Problems

4.105 Knowing that the allowable stress in section ABD is 10 ksi, deter-

mine the largest force P that can be applied to the bracket shown.

4.106 Portions of a

-in. square bar have been bent to form the two

machine components shown. Knowing that the allowable stress is

15 ksi, determine the maximum load that can be applied to each

component.

0.9 in.

2 in.

0.6 in.

Fig. P4.105

1 in.

(a)(b)

P'P P'P

Fig. P4.106

4.107 The four forces shown are applied to a rigid plate supported by

a solid steel post of radius a. Knowing that P 5 100 kN and a 5

40 mm, determine the maximum stress in the post when (a) the

force at D is removed, (b) the forces at C and D are removed.

Fig. P4.107

Fig. P4.108 and P4.109

12 kips

Fig. P4.110

4.108 A milling operation was used to remove a portion of a solid bar

of square cross section. Knowing that a 5 30 mm, d 5 20 mm,

and s

all

5 60 MPa, determine the magnitude P of the largest

forces that can be safely applied at the centers of the ends of

the bar.

4.109 A milling operation was used to remove a portion of a solid bar of

square cross section. Forces of magnitude P 5 18 kN are applied

at the centers of the ends of the bar. Knowing that a 5 30 mm

and s

all

5 135 MPa, determine the smallest allowable depth d of

the milled portion of the bar.

4.110 A short column is made by nailing two 1 3 4-in. planks to a 2 3

4-in. timber. Determine the largest compressive stress created in

the column by a 12-kip load applied as shown at the center of the

top section of the timber if (a) the column is as described, (b) plank

1 is removed, (c) both planks are removed.

bee80288_ch04_220-313.indd Page 275 10/26/10 4:31:23 PM user-f499bee80288_ch04_220-313.indd Page 275 10/26/10 4:31:23 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

276

Pure Bending

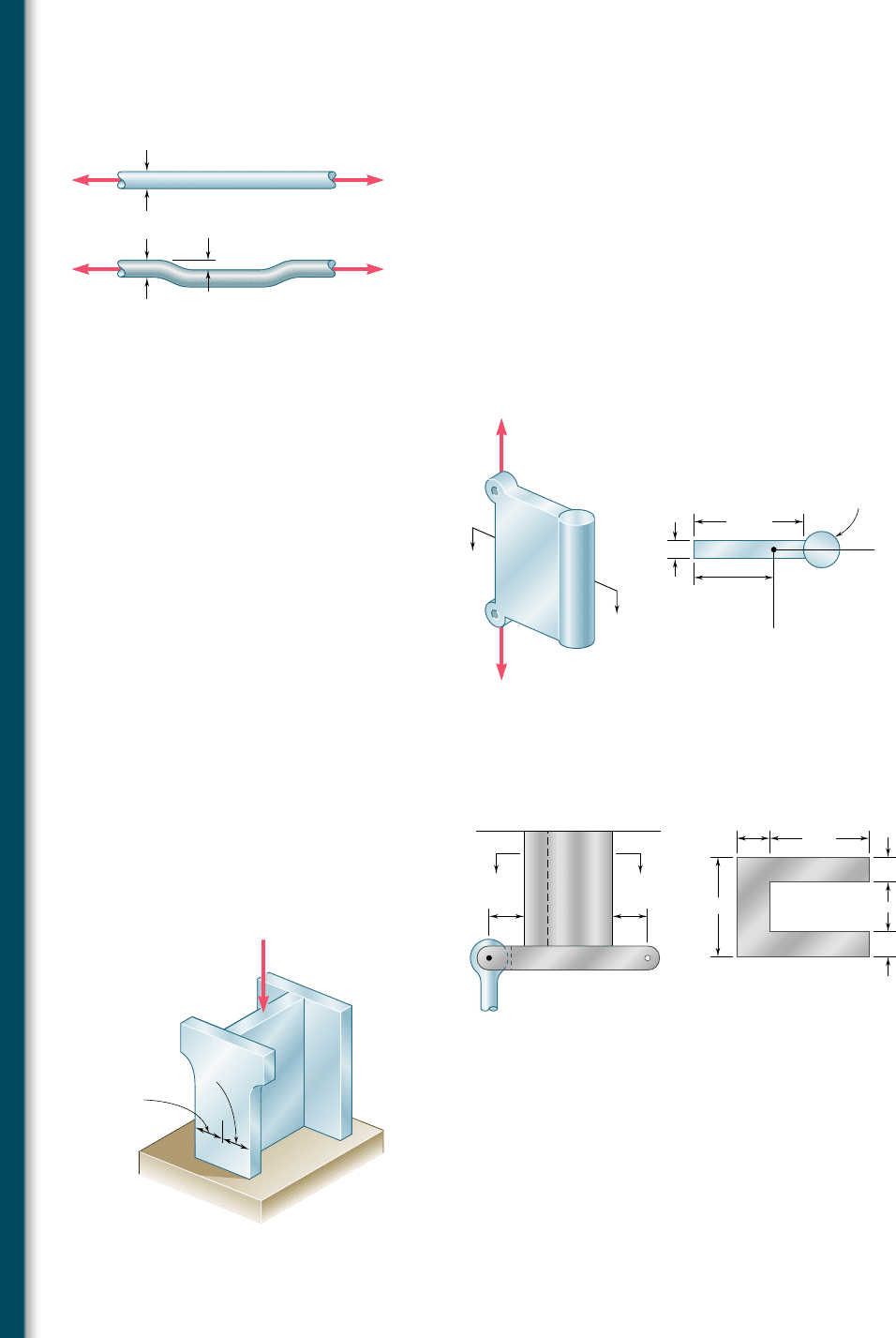
4.111 An offset h must be introduced into a solid circular rod of diameter

d. Knowing that the maximum stress after the offset is introduced

must not exceed 5 times the stress in the rod when it is straight,

determine the largest offset that can be used.

4.112 An offset h must be introduced into a metal tube of 0.75-in. outer

diameter and 0.08-in. wall thickness. Knowing that the maximum

stress after the offset is introduced must not exceed 4 times the

stress in the tube when it is straight, determine the largest offset

that can be used.

4.113 A steel rod is welded to a steel plate to form the machine element

shown. Knowing that the allowable stress is 135 MPa, determine

(a) the largest force P that can be applied to the element, (b) the

corresponding location of the neutral axis. Given: The centroid of

the cross section is at C and I

5 4195 mm

Fig . P4.111 and P4.112

3 mm

18 mm

13.12 mm

6-mm diamete

Section a-a

Fig. P4.113

4.114 A vertical rod is attached at point A to the cast iron hanger shown.

Knowing that the allowable stresses in the hanger are s

all

5 15 ksi

and s

all

5 212 ksi, determine the largest downward force and the

largest upward force that can be exerted by the rod.

0.75 in.

3 in.

1 in.

1.5 in. 1.5 in.

0.75 in.

Section a-a

Fig. P4.114

4.115 Solve Prob. 4.114, assuming that the vertical rod is attached at

point B instead of point A.

4.116 Three steel plates, each of 25 3 150-mm cross section, are welded

together to form a short H-shaped column. Later, for architectural

reasons, a 25-mm strip is removed from each side of one of the

flanges. Knowing that the load remains centric with respect to the

original cross section and that the allowable stress is 100 MPa,

determine the largest force P (a) that could be applied to the

original column, (b) that can be applied to the modified column.

50 mm

Fig. P4.116

bee80288_ch04_220-313.indd Page 276 10/26/10 4:31:35 PM user-f499bee80288_ch04_220-313.indd Page 276 10/26/10 4:31:35 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles