Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
287
SAMPLE PROBLEM 4.9
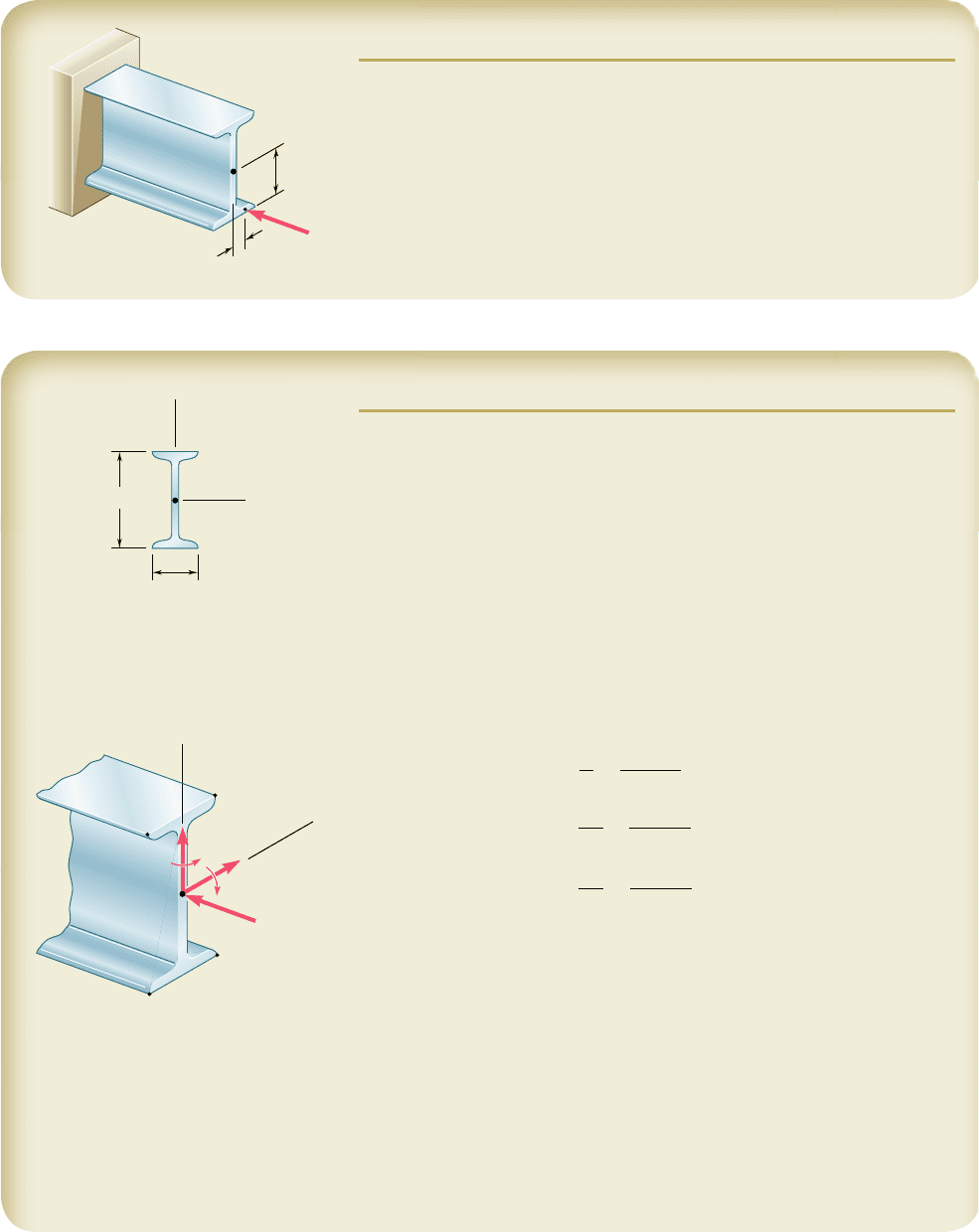
A horizontal load P is applied as shown to a short section of an S10 3 25.4
rolled-steel member. Knowing that the compressive stress in the member
is not to exceed 12 ksi, determine the largest permissible load P.
4.75 in.
1.5 in.
C
S10 25.4
P
SOLUTION
Properties of Cross Section. The following data are taken from
Appendix C.
Area: A 5 7.46 in
2
Section moduli: S
x
5 24.7 in
3
S
y
5 2.91 in
3
Force and Couple at C. We replace P by an equivalent force-couple
system at the centroid C of the cross section.
M
x
5 14.75 in.2PM
y
5 11.5 in.2P
Note that the couple vectors M
x
and M
y
are directed along the principal
axes of the cross section.
Normal Stresses. The absolute values of the stresses at points A, B,
D, and E due, respectively, to the centric load P and to the couples M
x
and
M
y
are
s
1
5
P
A
5
P
7
.
46 in
2
5 0.1340P
s
2
5
M
x
S
x
5
4.75P
24.7 in
3
5 0.1923P
s
3
5
M
y
S
y
5
1.5P
2.91 in
3
5 0.5155P
Superposition. The total stress at each point is found by superposing
the stresses due to P, M
x
, and M
y
. We determine the sign of each stress by
carefully examining the sketch of the force-couple system.
s
A
52s
1
1 s
2
1 s
3
520.1340P 1 0.1923P 1 0.5155P 510.574P
s
B
52s
1
1 s
2
2 s
3
520.1340P 1 0.1923P 2 0.5155P 520.457P
s
D
52s
1
2 s
2
1 s
3
520.1340P 2 0.1923P 1 0.5155P 510.189P
s
E
52s
1
2 s
2
2 s
3
520.1340P 2 0.1923P 2 0.5155P 520.842P
Largest Permissible Load. The maximum compressive stress occurs
at point E. Recalling that s
all
5 212 ksi, we write
s
a
ll
5 s
E
212
k
si 520.842P P 5 14.3
k
ipsb
C
y
x
4.66 in.
10 in.
y
x
A
B
C
P
M
x
M
y
D
E
bee80288_ch04_220-313.indd Page 287 10/27/10 5:46:24 PM user-f499bee80288_ch04_220-313.indd Page 287 10/27/10 5:46:24 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04
Apago PDF Enhancer
288
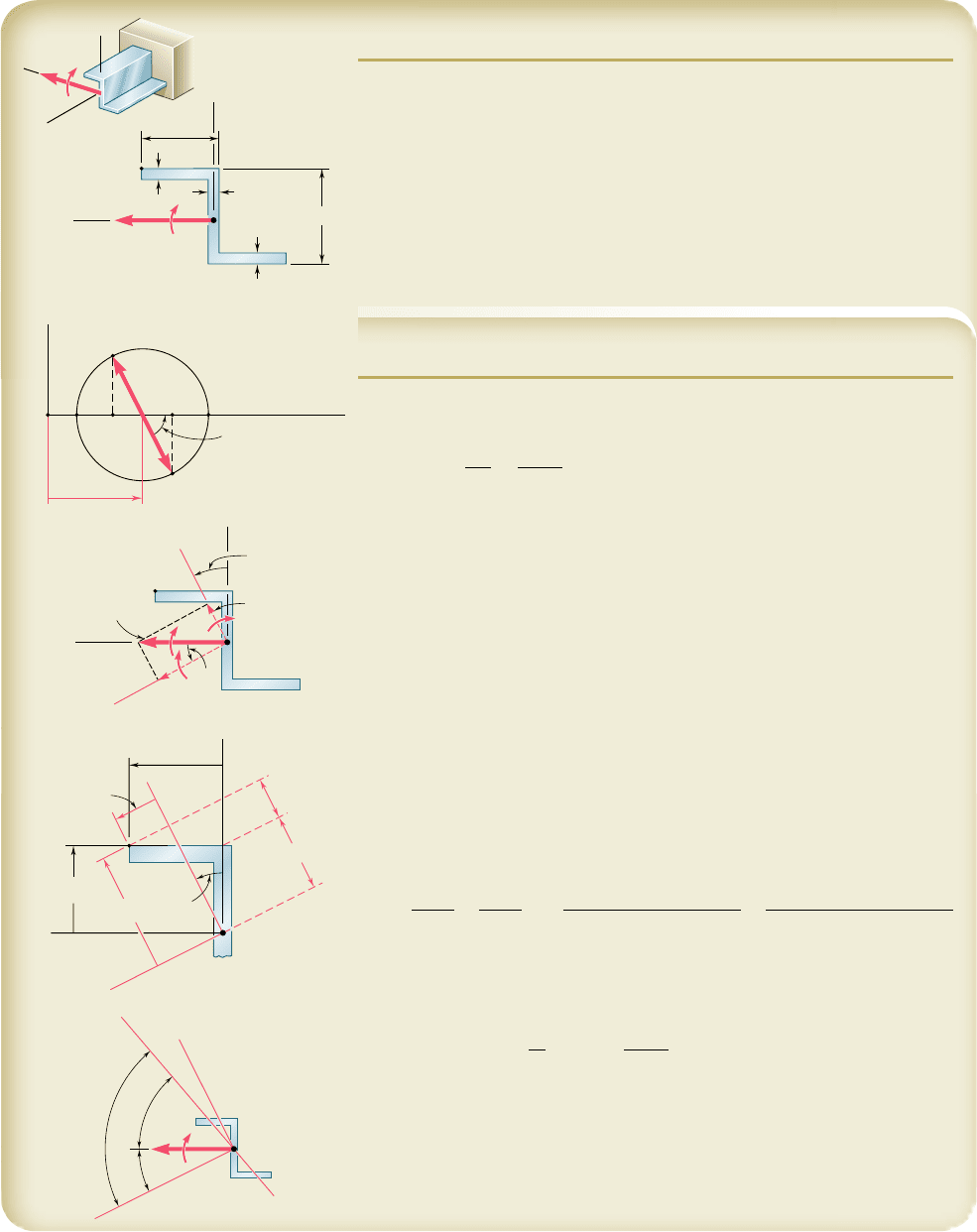
*SAMPLE PROBLEM 4.10
A couple of magnitude M
0
5 1.5 kN ? m acting in a vertical plane is applied
to a beam having the Z-shaped cross section shown. Determine (a) the stress
at point A, (b) the angle that the neutral axis forms with the horizontal plane.
The moments and product of inertia of the section with respect to the y
and z axes have been computed and are as follows:
I
y
5 3.25 3 10
2
6
m
4
I
z
5 4.18 3 10
2
6
m
4
I
yz
5 2.87 3 10
2
6
m
4
SOLUTION
Principal Axes. We draw Mohr’s circle and determine the orientation
of the principal axes and the corresponding principal moments of inertia.†
tan 2u
m
5
FZ
EF
5
2.8
7
0
.
465
2u
m
5 80.8°u
m
5 40.4°
R
2
5
1
EF
2
2
1
1
FZ
2
2
5
1
0.465
2
2
1
1
2.87
2
2
R 5 2.91 3 10
26
m
4
I
u
5 I
min
5 OU 5 I
ave
2 R 5 3.72 2 2.91 5 0.810 3 10
2
6
m
4
I
v
5 I
max
5 OV 5 I
ave
1 R 5 3.72 1 2.91 5 6.63 3 10
2
6
m
4
Loading. The applied couple M
0
is resolved into components parallel
to the principal axes.
M
u
5 M
0
sin u
m
5 1500 sin 40.4° 5 972 N ? m
M
v
5 M
0
cos u
m
5 1500 cos 40.4° 5 1142 N ? m
a. Stress at A. The perpendicular distances from each principal axis
to point A are
u
A
5 y
A
cos u
m
1 z
A
sin u
m
5 50 cos 40.4° 1 74 sin 40.4° 5 86.0 mm
v
A
52y
A
sin u
m
1 z
A
cos u
m
5250 sin 40.4° 1 74 cos 40.4° 5 23.9 mm
Considering separately the bending about each principal axis, we note that
M
u
produces a tensile stress at point A while M
v
produces a compressive
stress at the same point.
s
A
51
M
u
v
A
I
u
2
M
v
u
A
I
v
51
1
972 N ? m
21
0.0239 m
2
0.810 3 10
26
m
4
2
1
1142 N ? m
21
0.0860 m
2
6.63 3 10
26
m
4
5 1(28.68 MPa) 2 (14.81 MPa) s
A
5 113.87 MPa
◀
b. Neutral Axis. Using Eq. (4.57), we find the angle f that the
neutral axis forms with the v axis.
tan f 5
I
v
I
u
tan u
m
5
6.63
0.810
tan 40.4°f 5 81.8°
The angle b formed by the neutral axis and the horizontal is
b 5 f 2 u
m
5 81.88 2 40.48 5 41.48 b 5 41.48
◀
M
0
y
z
x
M
0
⫽ 1.5 kN · m
y
A
C
z
12 mm
12 mm
100 mm
12 mm
80 mm
I
yz
(10
–6
m
4
)
I
y
, I
z
(10
–6
m
4
)
I
ave
⫽ 3.72
Z(4.18, –2.87)
Y(3.25, 2.87)
OU D EF
R
R
V
2
m
M
0
⫽ 1.5 kN · m
M
u
M
v
m
⫽ 40.4°
m
y
u
A
C
z
v
z
A
⫽ 74 mm
z
v
z
A
sin
m
y
A
cos
m
m
y
A
⫽ 50 mm
y
u
C
A
v
A
u
A
u
v

M
0
m
C
N.A.
†See Ferdinand F. Beer and E. Russell Johnston, Jr., Mechanics for Engineers, 5th ed.,
McGraw-Hill, New York, 2008, or Vector Mechanics for Engineers–9th ed., McGraw-Hill,
New York, 2010, Secs. 9.8–9.10.
bee80288_ch04_220-313.indd Page 288 10/28/10 9:25:52 PM user-f499bee80288_ch04_220-313.indd Page 288 10/28/10 9:25:52 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
PROBLEMS
289
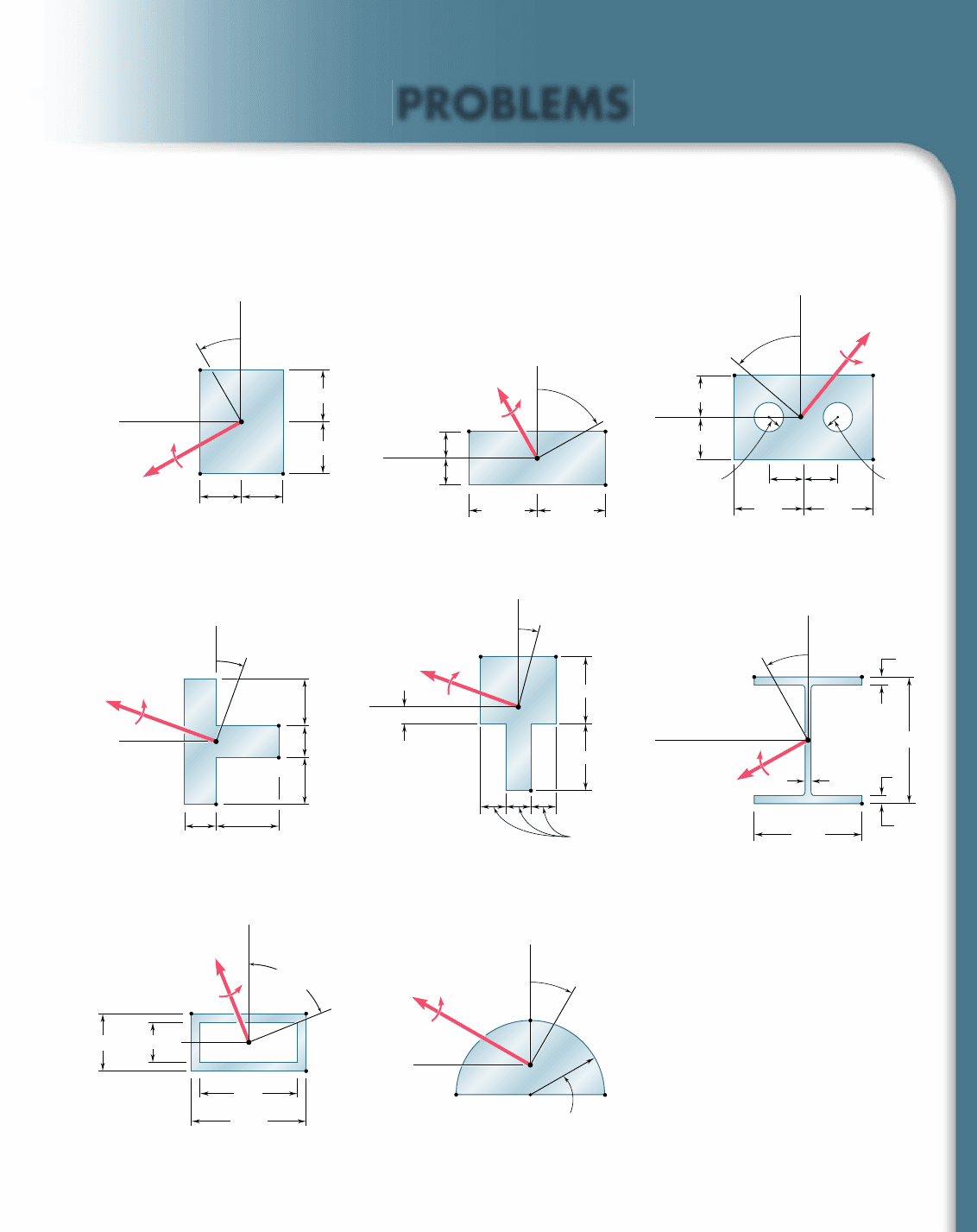
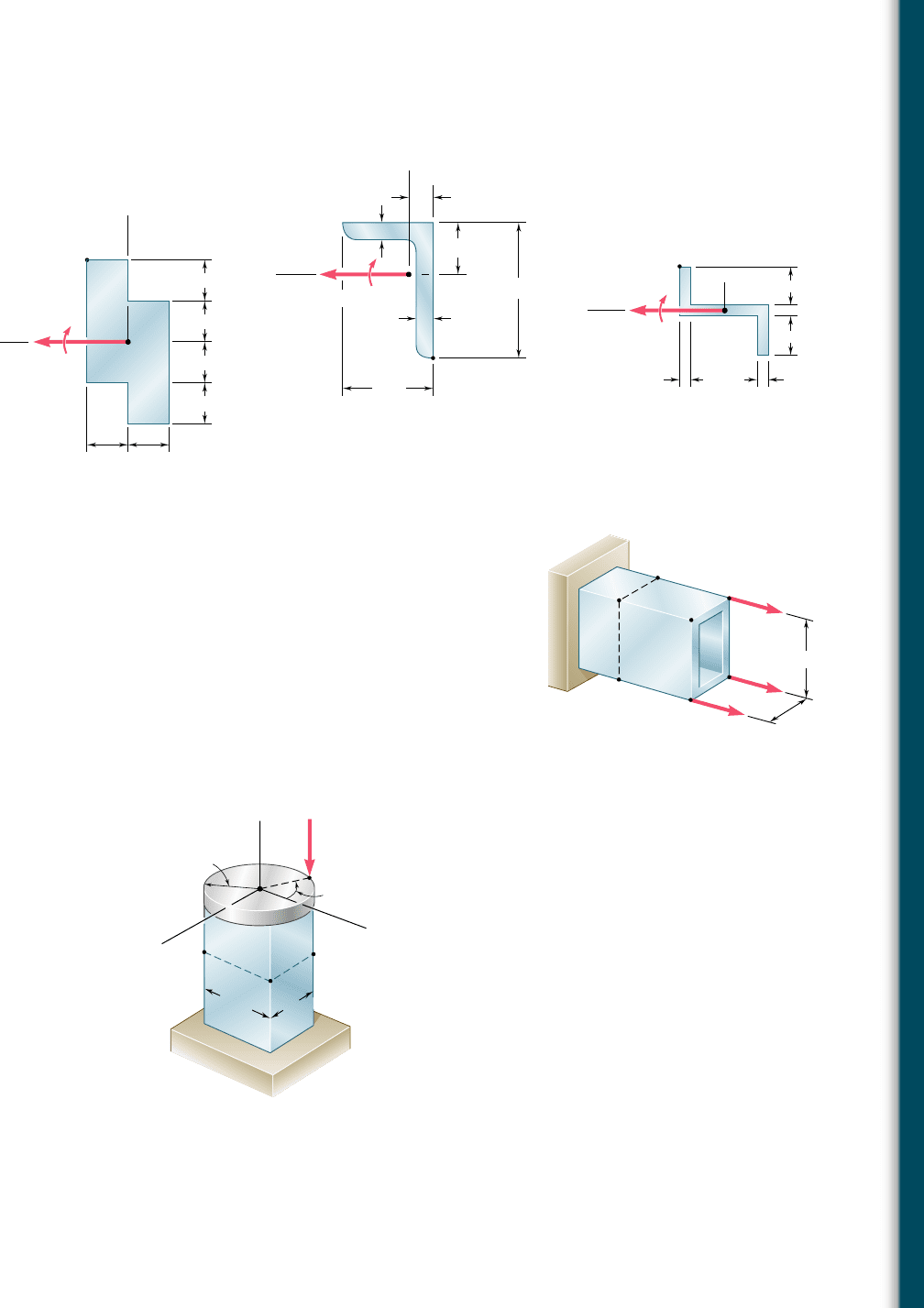
4.127 through 4.134 The couple M is applied to a beam of the cross
section shown in a plane forming an angle b with the vertical.
Determine the stress at (a) point A, (b) point B, (c) point D.
B
A
50 mm
50 mm
40 mm 40 mm
M 250 N · m
30
z
y
D
C
Fig. P4.127
A
60
B
z
y
16 mm
16 mm
40 mm 40 mm
M 300 N · m
D
C
Fig. P4.128
A
2.5 in.
5 in.
2.5 in.
3 in.
y
z
50
3 in.
1 in.1 in.
B
C
D
5 in.
M
60 kip · in.
Fig. P4.129
A
y
z
B
3 in.
2 in.
2 in. 4 in.
3 in.
C
M 10 kip · in.
20
D
A
B
10 in.
0.3 in.
0.5 in.
0.5 in.
8 in.
C
M 250 kip · in.
30
D
y
z
Fig. P4.132
M 25 kN · m
15
C
80 mm
80 mm
30 mm
20 mm
z
y
AB
D
Fig. P4.131Fig. P4.130
A
B
4 in.
1.6 in.2.4 in.
4.8 in.
C
M 75 kip · in.
75
D
y
z
Fig. P4.133
30
y
z
M 100 N · m
A
B
r 20 mm
C
D
Fig. P4.134
bee80288_ch04_220-313.indd Page 289 10/26/10 4:33:18 PM user-f499bee80288_ch04_220-313.indd Page 289 10/26/10 4:33:18 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
290
Pure Bending
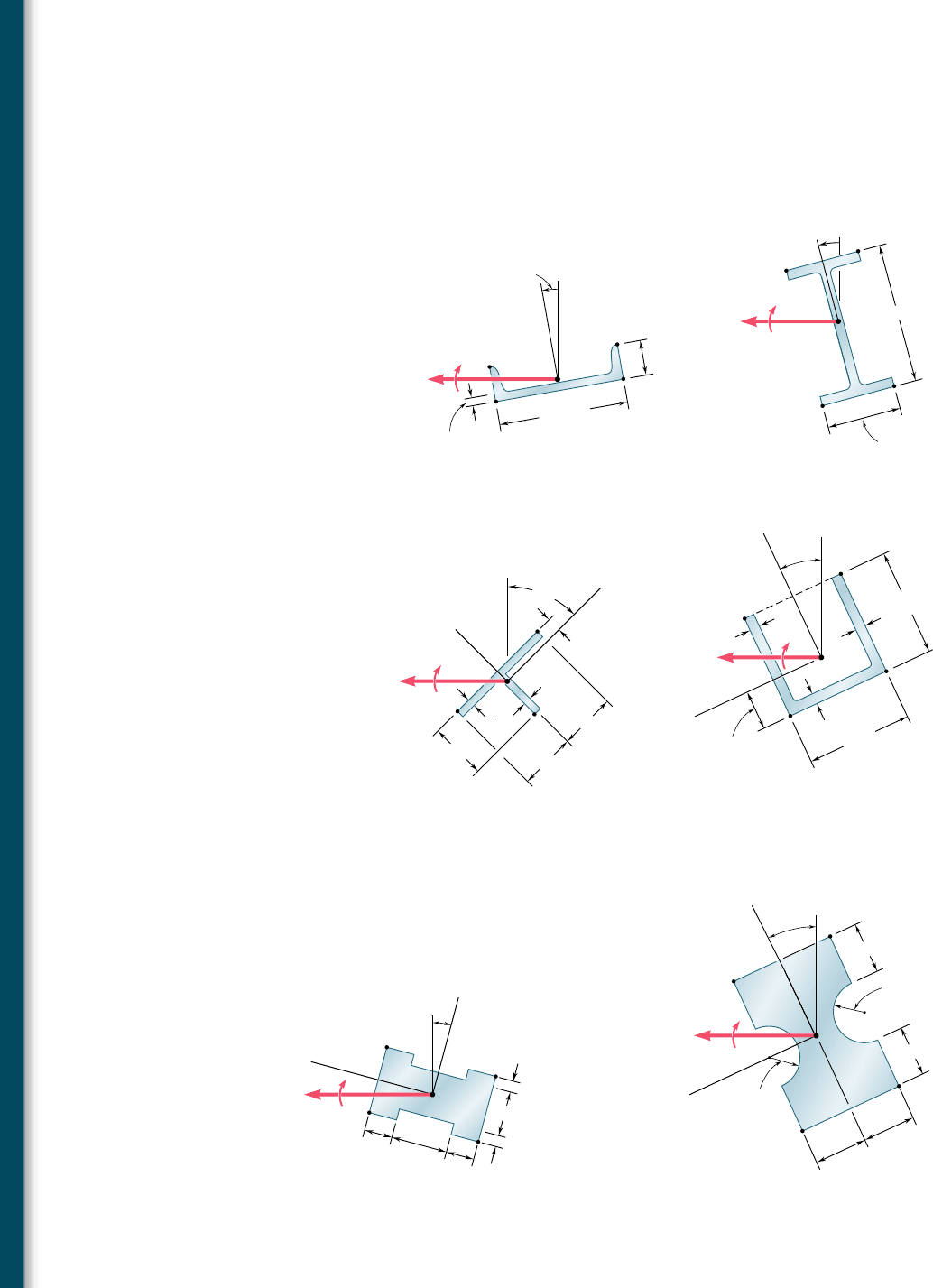
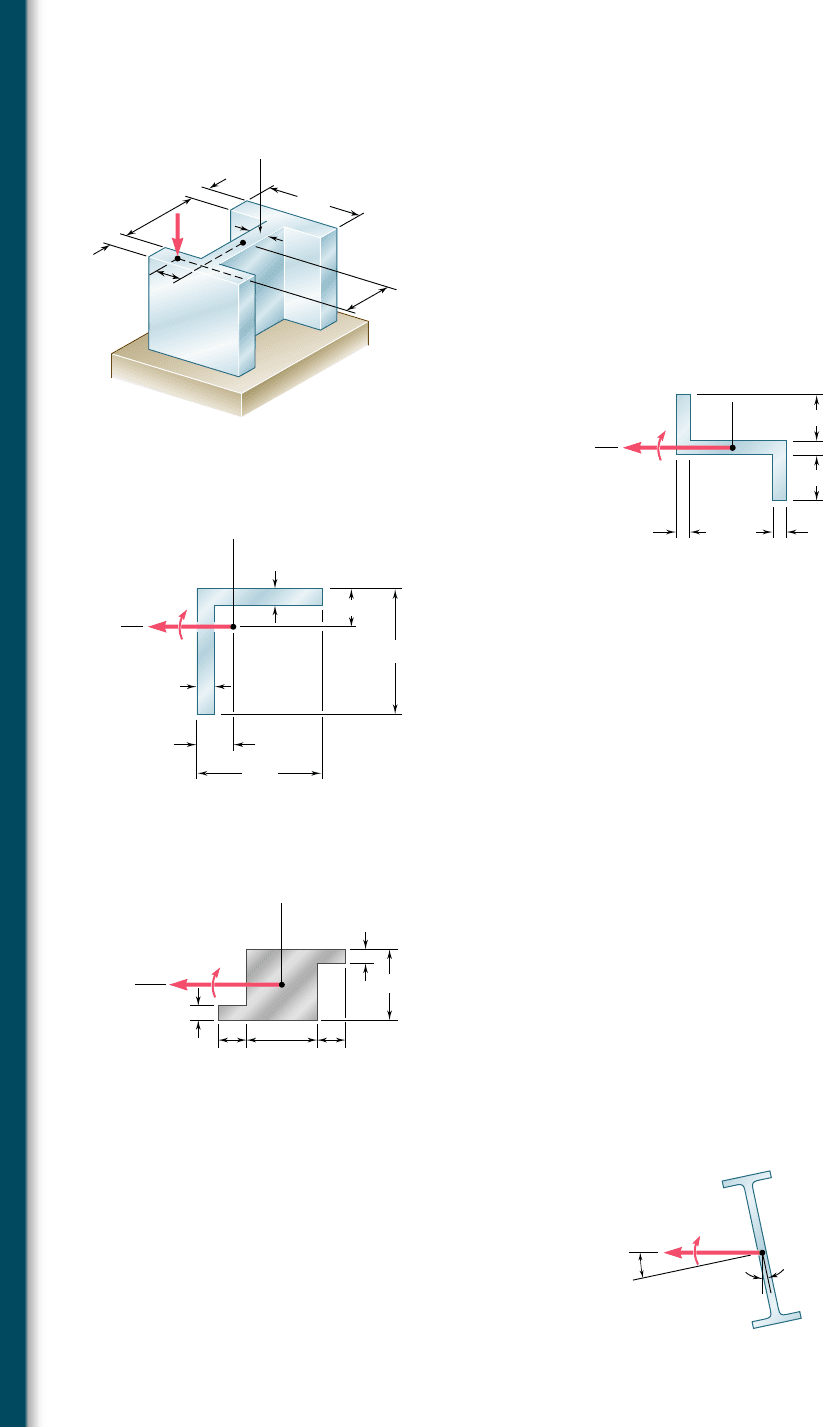
4.135 through 4.140 The couple M acts in a vertical plane and is
applied to a beam oriented as shown. Determine (a) the angle that
the neutral axis forms with the horizontal, (b) the maximum tensile
stress in the beam.
A
B
14.4 mm
C200 17.1
203 mm
57 mm
C
M 2.8 kN · m
D
E
10
Fig. P4.135
165 mm
310 mm
15
M 16 kN · m
W310 38.7
A
B
C
D
E
Fig. P4.136
A
B
in.
4 in.
4 in.
4 in.
0.859 in.
45
C
M 15 kip · in.
D
1
2
y'
z'
I
y'
6.74 in
4
I
z'
21.4 in
4
Fig. P4.137
A
B
C
M 400 N · m
30
D
E
5 mm
5 mm
18.57 mm
50 mm
50 mm
5 mm
z'
y'
I
y'
281 10
3
mm
4
I
z'
176.9 10
3
mm
4
Fig. P4.138
M 35 kip · in.
C
E
D
B
A
1 in.
1 in.
0.4 in.
0.4 in.
1.6 in.
2 in.
15
Fig. P4.139
A
M 120 N · m
20
D
B
E
10 mm
10 mm
10 mm
10 mm
6 mm
y'
z'
6 mm
C
I
y'
14.77 10
3
mm
4
I
z'
53.6 10
3
mm
4
Fig. P4.140
bee80288_ch04_220-313.indd Page 290 10/26/10 4:33:38 PM user-f499bee80288_ch04_220-313.indd Page 290 10/26/10 4:33:38 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
291
Problems
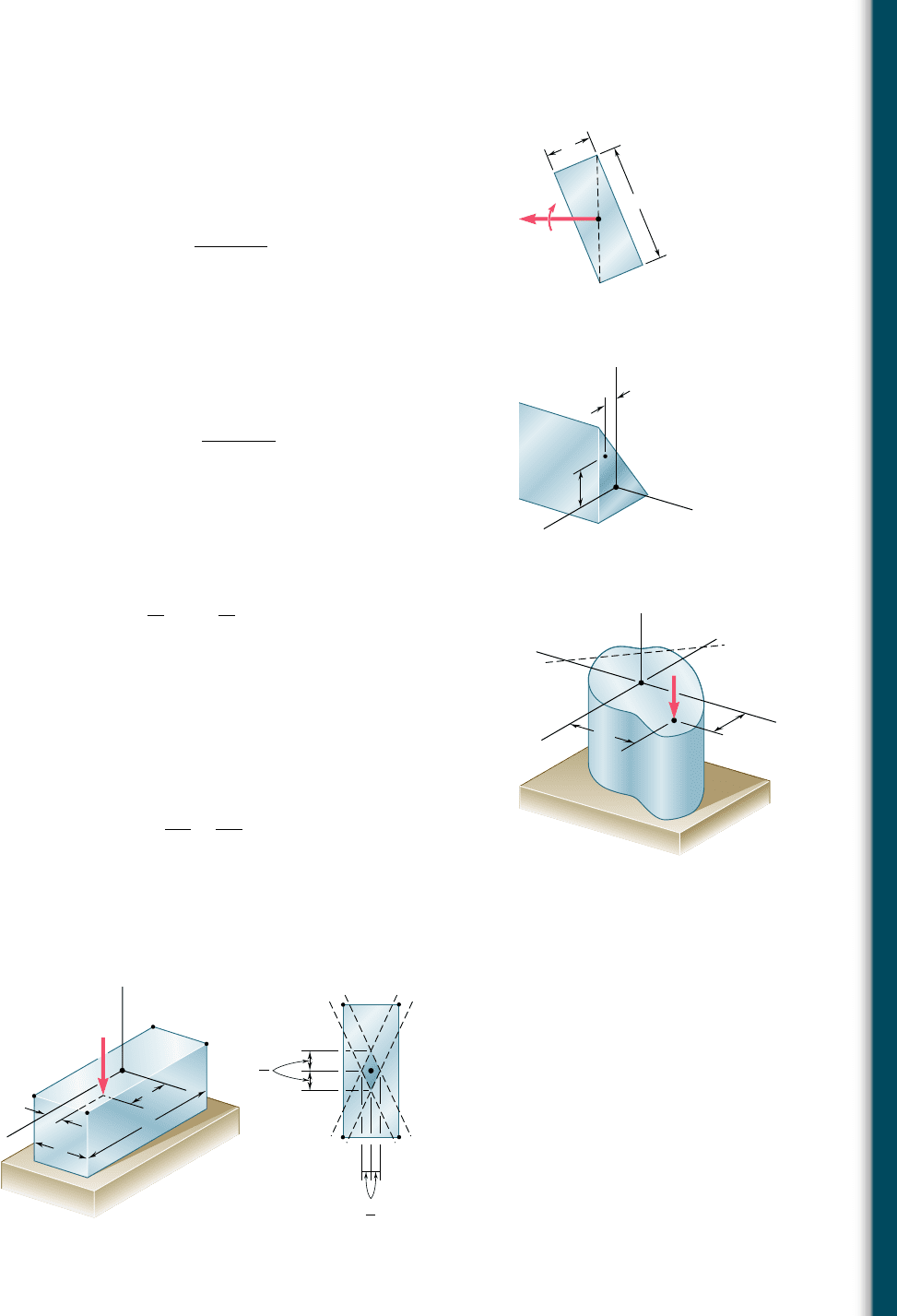
*4.141 through *4.143 The couple M acts in a vertical plane and is ap-
plied to a beam oriented as shown. Determine the stress at point A.
C
A
z
y
2.4 in.
2.4 in. 2.4 in.
2.4 in.
2.4 in.
2.4 in.
M 125 kip · in.
Fig. P4.141
A
6 in.
2.08 in.
1.08 in.
0.75 in.
0.75 in.
4 in.
C
M 60 kip · in.
y
z
I
y
8.7 in
4
I
yz
8.3 in
4
I
z
24.5 in
4
Fig. P4.142
A
40 mm
10 mm
40 mm
10 mm 10 mm70 mm
C
M 1.2 kN · m
y
z
I
y
1.894 10
6
mm
4
I
z
0.614 10
6
mm
4
I
yz
0.800 10
6
mm
4
Fig. P4.143
4.144 The tube shown has a uniform wall thickness of 12 mm. For the
loading given, determine (a) the stress at points A and B, (b) the
point where the neutral axis intersects line ABD.
4.145 Solve Prob. 4.144, assuming that the 28-kN force at point E is
removed.
4.146 A rigid circular plate of 125-mm radius is attached to a solid 150 3
200-mm rectangular post, with the center of the plate directly above
the center of the post. If a 4-kN force P is applied at E with u 5
308, determine (a) the stress at point A, (b) the stress at point B, (c)
the point where the neutral axis intersects line ABD.
75 mm
125 mm
28 kN
28 kN
14 kN
A
D
B
G
H
E
F
Fig. P4.144
y
A
B
E
D
C
z
x
R
125 mm
150 mm
200 mm
P
4 kN
Fig. P4.146
4.147 In Prob. 4.146, determine (a) the value of u for which the stress
at D reaches its largest value, (b) the corresponding values of the
stress at A, B, C, and D.
bee80288_ch04_220-313.indd Page 291 10/26/10 4:33:51 PM user-f499bee80288_ch04_220-313.indd Page 291 10/26/10 4:33:51 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
292
Pure Bending
4.148 Knowing that P 5 90 kips, determine the largest distance a for
which the maximum compressive stress does not exceed 18 ksi.
4.149 Knowing that a 5 1.25 in., determine the largest value of P that can be
applied without exceeding either of the following allowable stresses:
s
ten
5 10 ksi s
comp
5 18 ksi
4.150 The Z section shown is subjected to a couple M
0
acting in a vertical
plane. Determine the largest permissible value of the moment M
0
of the couple if the maximum stress is not to exceed 80 MPa.
Given: I
max
5 2.28 3 10
26
m
4
, I
min
5 0.23 3 10
26
m
4
, principal
axes 25.78 c and 64.38 a.
1 in.
1 in.
1 in.
4 in.
5 in.
2.5 in.
P
a
Fig. P4.148 and P4.149
C
40 mm
10 mm 10 mm
10 mm
70 mm
y
z
40 mm
M
0
Fig. P4.150
4.151 Solve Prob. 4.150, assuming that the couple M
0
acts in a horizontal
plane.
4.152 A beam having the cross section shown is subjected to a couple M
0
that acts in a vertical plane. Determine the largest permissible value
of the moment M
0
of the couple if the maximum stress in the beam is
not to exceed 12 ksi. Given: I
y
5 I
z
5 11.3 in
4
, A 5 4.75 in
2
, k
min
5
0.983 in. (Hint: By reason of symmetry, the principal axes form an
angle of 458 with the coordinate axes. Use the relations I
min
5 Ak
2
min
and I
min
1 I
max
5 I
y
1 I
z
.)
4.153 Solve Prob. 4.152, assuming that the couple M
0
acts in a horizontal
plane.
4.154 An extruded aluminum member having the cross section shown is
subjected to a couple acting in a vertical plane. Determine the
largest permissible value of the moment M
0
of the couple if the
maximum stress is not to exceed 12 ksi. Given: I
max
5 0.957 in
4
,
I
min
5 0.427 in
4
, principal axes 29.48 a and 60.68 c.
4.155 A couple M
0
acting in a vertical plane is applied to a W12 3 16
rolled-steel beam, whose web forms an angle u with the vertical.
Denoting by s
0
the maximum stress in the beam when u 5 0,
determine the angle of inclination u of the beam for which the
maximum stress is 2s
0
.
C
0.5 in.
5 in.
1.43 in.
1.43 in.
5 in.
0.5 in.
y
z
M
0
Fig. P4.152
1.5 in.
0.3 in.
1.5 in.0.6 in.
0.3 in.
0.6 in.
M
0
y
z
C
Fig. P4.154
M
0
Fig. P4.155
bee80288_ch04_220-313.indd Page 292 10/26/10 4:34:02 PM user-f499bee80288_ch04_220-313.indd Page 292 10/26/10 4:34:02 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
293
Problems
4.156 Show that, if a solid rectangular beam is bent by a couple applied
in a plane containing one diagonal of a rectangular cross section,
the neutral axis will lie along the other diagonal.
4.157 A beam of unsymmetric cross section is subjected to a couple M
0
acting in the horizontal plane xz. Show that the stress at point A,
of coordinates y and z, is
s
A
5
z
I
z
2 y
I
yz
I
y
I
z
2 I
2
yz
M
y
where I
y
, I
z
, and I
yz
denote the moments and product of inertia of
the cross section with respect to the coordinate axes, and M
y
the
moment of the couple.
4.158 A beam of unsymmetric cross section is subjected to a couple M
0
acting in the vertical plane xy. Show that the stress at point A, of
coordinates y and z, is
s
A
52
y
I
y
2 z
I
yz
I
y
I
z
2 I
2
yz
M
z
where I
y
, I
z
, and I
yz
denote the moments and product of inertia of
the cross section with respect to the coordinate axes, and M
z
the
moment of the couple.
4.159 (a) Show that, if a vertical force P is applied at point A of the sec-
tion shown, the equation of the neutral axis BD is
a
x
A
r
2
z
b
x 1
a
z
A
r
2
x
b
z 521
where r
z
and r
x
denote the radius of gyration of the cross section
with respect to the z axis and the x axis, respectively. (b) Further
show that, if a vertical force Q is applied at any point located on
line BD, the stress at point A will be zero.
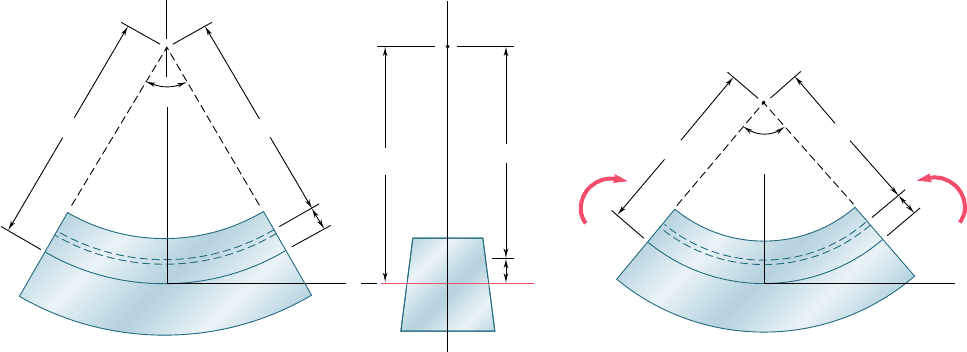
4.160 (a) Show that the stress at corner A of the prismatic member
shown in Fig. P4.160a will be zero if the vertical force P is applied
at a point located on the line
x
b
y
6
1
z
h
y
6
5 1
(b) Further show that, if no tensile stress is to occur in the member, the
force P must be applied at a point located within the area bounded
by the line found in part a and three similar lines corresponding to
the condition of zero stress at B, C, and D, respectively. This area,
shown in Fig. P4.160b, is known as the kern of the cross section.
M
A
B
E
C
D
h
b
Fig. P4.156
A
C
y
y
z
z
x
Fig. P4.157 and P4.158
A
B
C
P
D
y
x
z
x
A
z
A
Fig. P4.159
A
A
B
B
C
C
D
D
z
z
x
x
b
h
y
h
6
b
6
(a)(b)
P
Fig. P4.160
bee80288_ch04_220-313.indd Page 293 10/26/10 4:34:11 PM user-f499bee80288_ch04_220-313.indd Page 293 10/26/10 4:34:11 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
294
Pure Bending
*4.15 BENDING OF CURVED MEMBERS
Our analysis of stresses due to bending has been restricted so far to
straight members. In this section we will consider the stresses caused
by the application of equal and opposite couples to members that
are initially curved. Our discussion will be limited to curved mem-
bers of uniform cross section possessing a plane of symmetry in
which the bending couples are applied, and it will be assumed that
all stresses remain below the proportional limit.
If the initial curvature of the member is small, i.e., if its radius
of curvature is large compared to the depth of its cross section, a good
approximation can be obtained for the distribution of stresses by
assuming the member to be straight and using the formulas derived
in Secs. 4.3 and 4.4.† However, when the radius of curvature and the
dimensions of the cross section of the member are of the same order
of magnitude, we must use a different method of analysis, which was
first introduced by the German engineer E. Winkler (1835–1888).
Consider the curved member of uniform cross section shown in
Fig. 4.70. Its transverse section is symmetric with respect to the y axis
(Fig. 4.70b) and, in its unstressed state, its upper and lower surfaces
intersect the vertical xy plane along arcs of circle AB and FG centered
at C (Fig. 4.70a). We now apply two equal and opposite couples M
†See Prob. 4.166.
R
R
A
J
D
F
G
E
B
K
y
r
r
C
C
y
y
y
x xz
(a)(b)(c)
N. A.
F'
D'
J'
A'
R'
M
M'
C'
r'
B'
K'
E'
y
y
G'
'
Fig. 4.70 Curved member in pure bending.
and M9 in the plane of symmetry of the member (Fig. 4.70c). A rea-
soning similar to that of Sec. 4.3 would show that any transverse plane
section containing C will remain plane, and that the various arcs of
circle indicated in Fig. 4.70a will be transformed into circular and
concentric arcs with a center C9 different from C. More specifically,
if the couples M and M9 are directed as shown, the curvature of the
various arcs of circle will increase; that is A9C9 , AC. We also note
that the couples M and M9 will cause the length of the upper surface
bee80288_ch04_220-313.indd Page 294 10/26/10 4:34:21 PM user-f499bee80288_ch04_220-313.indd Page 294 10/26/10 4:34:21 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
295
of the member to decrease (A9B9 , AB) and the length of the lower
surface to increase (F9G9 . FG). We conclude that a neutral surface
must exist in the member, the length of which remains constant. The
intersection of the neutral surface with the xy plane has been repre-
sented in Fig. 4.70a by the arc DE of radius R, and in Fig. 4.70c by
the arc D9E9 of radius R9. Denoting by u and u9 the central angles
corresponding respectively to DE and D9E9, we express the fact that
the length of the neutral surface remains constant by writing
Ru 5 R9u9 (4.59)
Considering now the arc of circle JK located at a distance y
above the neutral surface, and denoting respectively by r and r9 the
radius of this arc before and after the bending couples have been
applied, we express the deformation of JK as
d 5 r9u9 2 ru (4.60)
Observing from Fig. 4.70 that
r 5 R 2 y r9 5 R9 2 y (4.61)
and substituting these expressions into Eq. (4.60), we write
d 5 (R9 2 y)u9 2 (R 2 y)u
or, recalling Eq. (4.59) and setting u9 2 u 5 Du,
d 5 2y Du (4.62)
The normal strain P
x
in the elements of JK is obtained by dividing
the deformation d by the original length ru of arc JK. We write
P
x
5
d
ru
52
y
¢u
ru
or, recalling the first of the relations (4.61),
P
x
52
¢u
u
y
R 2 y
(4.63)
The relation obtained shows that, while each transverse section
remains plane, the normal strain P
x
does not vary linearly with the
distance y from the neutral surface.
The normal stress s
x
can now be obtained from Hooke’s law,
s
x
5 EP
x
, by substituting for P
x
from Eq. (4.63). We have
s
x
52
E ¢u
u
y
R 2 y
(4.64)
or, alternatively, recalling the first of Eqs. (4.61),
s
x
52
E ¢u
u
R 2 r
r
(4.65)
Equation (4.64) shows that, like P
x
, the normal stress s
x
does not
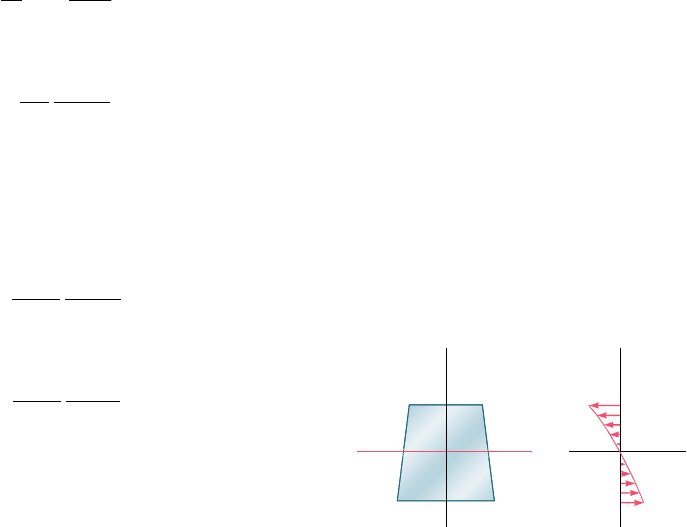
vary linearly with the distance y from the neutral surface. Plotting
s
x
versus y, we obtain an arc of hyperbola (Fig. 4.71).
In order to determine the location of the neutral surface in the
member and the value of the coefficient E Duyu used in Eqs. (4.64)
4.15 Bending of Curved Members
N. A.
y
z
x
y
Fig. 4.71
bee80288_ch04_220-313.indd Page 295 10/26/10 4:34:21 PM user-f499bee80288_ch04_220-313.indd Page 295 10/26/10 4:34:21 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
296
Pure Bending
and (4.65), we now recall that the elementary forces acting on any
transverse section must be statically equivalent to the bending couple
M. Expressing, as we did in Sec. 4.2 for a straight member, that the
sum of the elementary forces acting on the section must be zero,
and that the sum of their moments about the transverse z axis must
be equal to the bending moment M, we write the equations
#
s
x
dA 5 0 (4.1)
and
#
12ys
x
dA25 M (4.3)
Substituting for s
x
from (4.65) into Eq. (4.1), we write
2
#
E ¢u
u
R 2 r
r
dA 5 0
#
R 2 r
r
dA 5 0
R
#
dA
r
2
#
dA 5 0
from which it follows that the distance R from the center of curva-
ture C to the neutral surface is defined by the relation
R 5
A
#
dA
r
(4.66)
We note that the value obtained for R is not equal to the dis-
tance
r from C to the centroid of the cross section, since r is defined
by a different relation, namely,
r 5
1
A
#
r dA
(4.67)
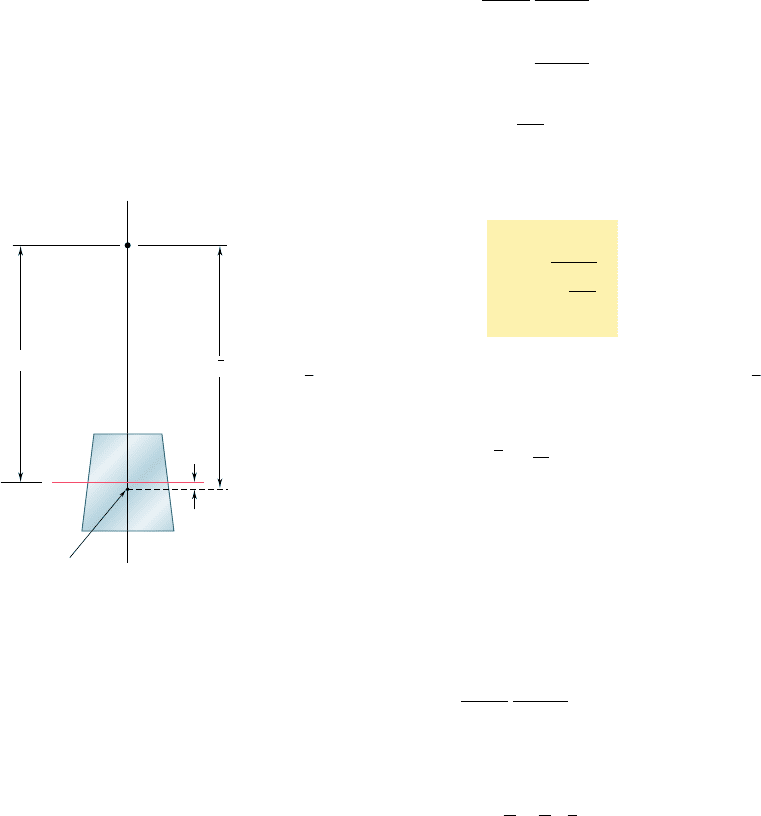
We thus conclude that, in a curved member, the neutral axis of a
transverse section does not pass through the centroid of that section
(Fig. 4.72).† Expressions for the radius R of the neutral surface will
be derived for some specific cross-sectional shapes in Example 4.10
and in Probs. 4.188 through 4.190. For convenience, these expres-
sions are shown in Fig. 4.73.
Substituting now for s
x
from (4.65) into Eq. (4.3), we write
#
E ¢u
u
R 2 r
r
y dA 5 M
†However, an interesting property of the neutral surface can be noted if we write Eq.
(4.66) in the alternative form
1
R
5
1
A
#
1
r
dA
(4.669)
Equation (4.669) shows that, if the member is divided into a large number of fibers of
cross-sectional area dA, the curvature 1yR of the neutral surface will be equal to the aver-
age value of the curvature 1yr of the various fibers.
N. A.
Centroid
z
y
C
R
e
r
Fig. 4.72
bee80288_ch04_220-313.indd Page 296 10/26/10 4:34:22 PM user-f499bee80288_ch04_220-313.indd Page 296 10/26/10 4:34:22 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
