Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

or, since y 5 R 2 r,

E ¢

1R 2 r2

dA 5 M

Expanding the square in the integrand, we obtain after reductions

E ¢

2 2RA 1

r dA d5 M

Recalling Eqs. (4.66) and (4.67), we note that the first term in the

brackets is equal to RA, while the last term is equal to

rA. We have,

therefore,

E ¢

1RA 2 2RA 1 rA25 M

and, solving for E Duyu,

E ¢

r 2 R

(4.68)

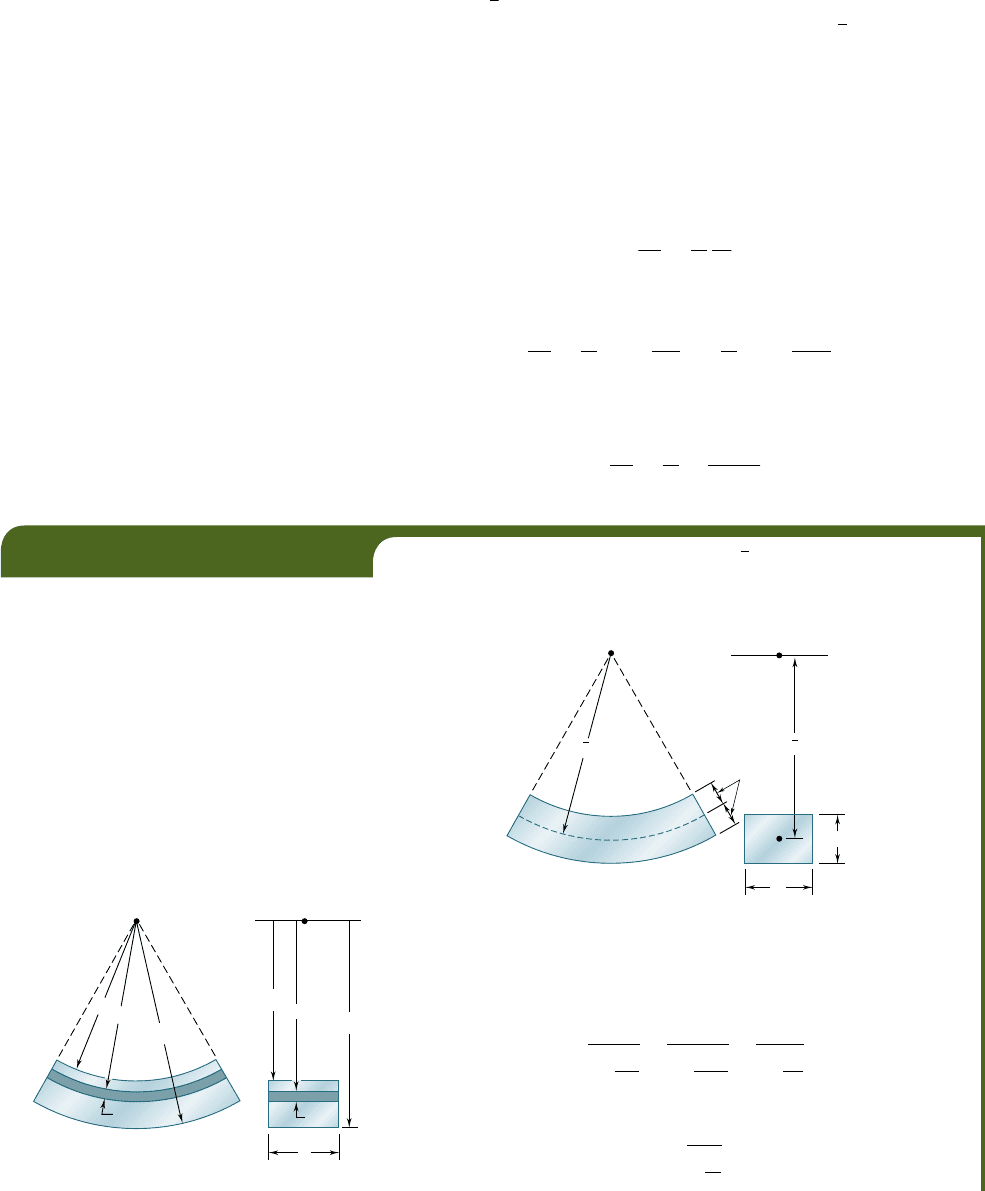
Referring to Fig. 4.70, we note that Du . 0 for M . 0. It follows

that

r 2 R . 0, or R , r, regardless of the shape of the section.

Thus, the neutral axis of a transverse section is always located between

the centroid of the section and the center of curvature of the mem-

ber (Fig. 4.72). Setting

r 2 R 5 e, we write Eq. (4.68) in the form

E ¢

(4.69)

Substituting now for E Duyu from (4.69) into Eqs. (4.64) and (4.65),

we obtain the following alternative expressions for the normal stress

in a curved beam:

Ae1R 2 y2

(4.70)

and

r 2 R

Aer

(4.71)

297

R 

Rectangle

R  R 

 1

TriangleCircle

(r  r

 c

)

R 

 b

)

 h(b

 b

)(b

 b

)

Trapezoid

Fig. 4.73 Radius of neutral surface for various cross-sectional shapes.

bee80288_ch04_220-313.indd Page 297 11/11/10 3:03:19 PM user-f499bee80288_ch04_220-313.indd Page 297 11/11/10 3:03:19 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

298

Pure Bending

We should note that the parameter e in the previous equations

is a small quantity obtained by subtracting two lengths of comparable

size, R and

r. In order to determine s

with a reasonable degree of

accuracy, it is therefore necessary to compute R and

r very accurately,

particularly when both of these quantities are large, i.e., when the

curvature of the member is small. However, as we indicated earlier,

it is possible in such a case to obtain a good approximation for s

using the formula s

5 2MyyI developed for straight members.

Let us now determine the change in curvature of the neutral sur-

face caused by the bending moment M. Solving Eq. (4.59) for the cur-

vature 1yR9 of the neutral surface in the deformed member, we write

R¿

u¿

or, setting u9 5 u 1 Du and recalling Eq. (4.69),

R¿

1 1

¢u

1 1

EAe

from which it follows that the change in curvature of the neutral

surface is

R¿

EAeR

(4.72)

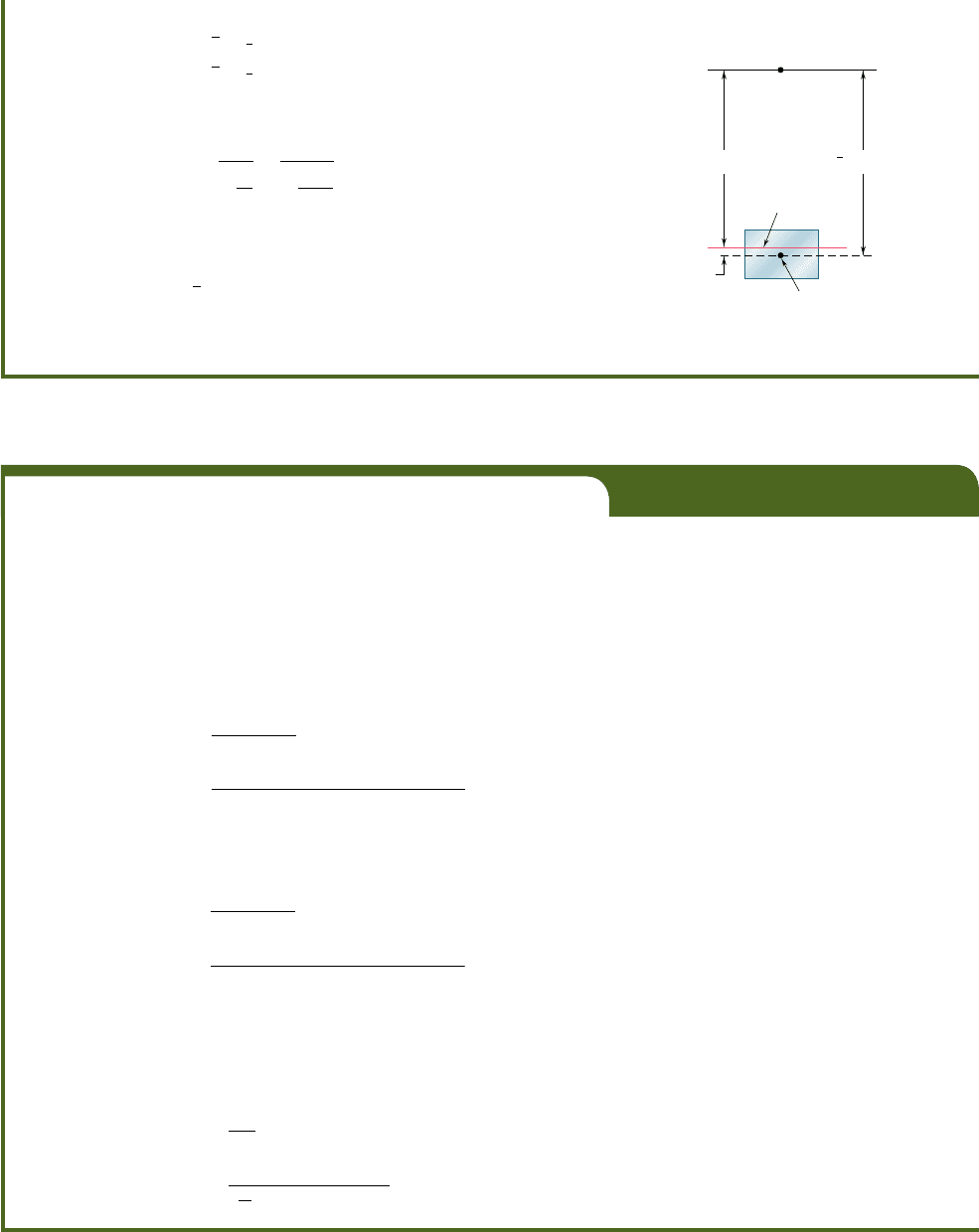
A curved rectangular bar has a mean radius r 5 6 in

and a cross section

of width b 5 2.5 in. and depth h 5 1.5 in. (Fig. 4.74). Determine the

distance e between the centroid and the neutral axis of the cross section.

EXAMPLE 4.10

h/2

Fig. 4.74

We first derive the expression for the radius R of the neutral sur-

face. Denoting by r

and r

, respectively, the inner and outer radius of

the bar (Fig. 4.75), we use Eq. (4.66) and write

R 5

b dr

R 5

(4.73)

Fig. 4.75

bee80288_ch04_220-313.indd Page 298 10/26/10 4:34:31 PM user-f499bee80288_ch04_220-313.indd Page 298 10/26/10 4:34:31 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

For the given data, we have

5 r 2

h 5 6 2 0.75 5 5.25 in.

5 r 1

h 5 6 1 0.75 5 6.75 in.

Substituting for h, r

, and r

into Eq. (4.73), we have

R 5

1.5 in.

6.75

5.25

5 5.9686 in.

The distance between the centroid and the neutral axis of the cross sec-

tion (Fig. 4.76) is thus

5 r 2 R 5 6 2 5

9686 5 0

0314 in

We note that it was necessary to calculate R with five significant figures

in order to obtain e with the usual degree of accuracy.

r  6 in.

R  5.9686 in.

e  0.0314 in.

Neutral axis

Centroid

Fig. 4.76

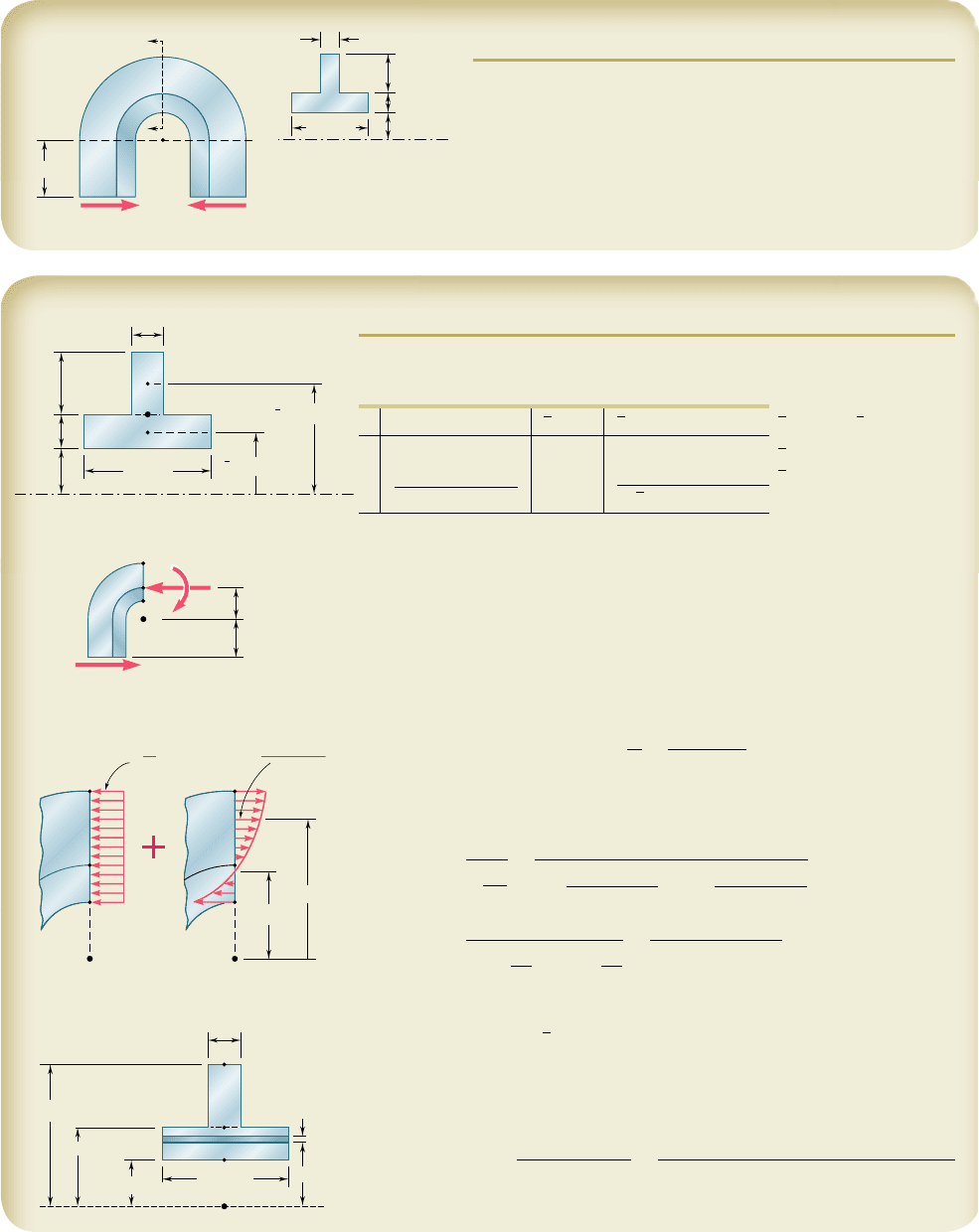
For the bar of Example 4.10, determine the largest tensile and compressive

stresses, knowing that the bending moment in the bar is M 5 8 kip ? in.

We use Eq. (4.71) with the given data,

M 5 8 kip ? in. A 5 bh 5 (2.5 in.)(1.5 in.) 5 3.75 in

and the values obtained in Example 4.10 for R and e,

R 5 5.969 e 5 0.0314 in.

Making first r 5 r

5 6.75 in. in Eq. (4.71), we write

max

2 R

Aer

8 kip ? in.

6.75 in. 2 5.969 in.

3.75 in

0.0314 in.

6.75 in.

5 7.86

Making now r 5 r

5 5.25 in. in Eq. (4.71), we have

min

2 R

Aer

8 kip ? in.

5.25 in. 2 5.969 in.

3.75 in

0.0314 in.

5.25 in.

min

529.30

Remark. Let us compare the values obtained for s

max

and s

min

with

the result we would get for a straight bar. Using Eq. (4.15) of Sec. 4.4, we

write

max, min

8 kip ? in.

0.75 in.

2.5 in.

1.5 in.

568.53 ksi

299

EXAMPLE 4.11

bee80288_ch04_220-313.indd Page 299 10/27/10 5:46:26 PM user-f499bee80288_ch04_220-313.indd Page 299 10/27/10 5:46:26 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

300

SAMPLE PROBLEM 4.11

A machine component has a T-shaped cross section and is

loaded as shown. Knowing that the allowable compressive

stress is 50 MPa, determine the largest force P that can be

applied to the component.

SOLUTION

Centroid of the Cross Section. We locate the centroid D of the cross

section

, mm

5 1600 40 64 3 10

2400

5 120 3 10

5 800 70 56 3 10

r 5 50 mm 5 0.050 m

5 2400 © r

5 120 3 10

Force and Couple at D. The internal forces in section a-a are equiva-

lent to a force P acting at D and a couple M of moment

M 5 P(50 mm 1 60 mm) 5 (0.110 m)P

Superposition. The centric force P causes a uniform compressive

stress on section a-a. The bending couple M causes a varying stress distribu-

tion [Eq. (4.71)]. We note that the couple M tends to increase the curvature

of the member and is therefore positive (cf. Fig. 4.70). The total stress at a

point of section a-a located at distance r from the center of curvature C is

s 52

r 2 R

Aer

(1)

Radius of Neutral Surface. We now determine the radius R of the

neutral surface by using Eq. (4.66).

R 5

2400 mm

180 mm2 d

120 mm2 d

2400

80 ln

1 20 ln

2400

40.866 1 11.756

5 45.61 mm

5 0

04561 m

We also compute:

5 r 2 R 5 0

05000 m 2 0

04561 m 5 0

00439 m

Allowable Load. We observe that the largest compressive stress will

occur at point A where r 5 0.030 m. Recalling that s

all

5 50 MPa and using

Eq. (1), we write

250 3 10

Pa 52

2.4 3 10

0.110 P

0.030 m 2 0.04561 m

2.4 3 10

0.00439 m

0.030 m

250 3 10

52417P 2 5432P P 5 8.55 kN

◀

60 mm

20 mm

Section a-a

40 mm

20 mm

30 mm80 mm

P' P

40 mm

20 mm

 40 mm

20 mm

30 mm

80 mm

 70 mm

50 mm

60 mm





–

M (r – R)

Aer





20 mm

80 mm

 90 mm

 50 mm

 30 mm

bee80288_ch04_220-313.indd Page 300 11/11/10 3:03:20 PM user-f499bee80288_ch04_220-313.indd Page 300 11/11/10 3:03:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

PROBLEMS

301

4.161 For the machine component and loading shown, determine the

stress at point A when (a) h 5 2 in., (b) h 5 2.6 in.

4.162 For the machine component and loading shown, determine the

stress at points A and B when h 5 2.5 in.

4.163 The curved portion of the bar shown has an inner radius of 20 mm.

Knowing that the allowable stress in the bar is 150 MPa, determine

the largest permissible distance a from the line of action of the

3-kN force to the vertical plane containing the center of curvature

of the bar.

4.164 The curved portion of the bar shown has an inner radius of 20 mm.

Knowing that the line of action of the 3-kN force is located at a

distance a 5 60 mm from the vertical plane containing the center

of curvature of the bar, determine the largest compressive stress

in the bar.

4.165 The curved bar shown has a cross section of 40 3 60 mm and an

inner radius r

5 15 mm. For the loading shown determine the

largest tensile and compressive stresses.

0.75 in.

4 kip · in.

3 in.

4 kip · in.

Fig. P4.161 and P4.162

25 mm

r  20 mm

P  3 kN

Fig. P4.163 and P4.164

40 mm

60 mm

120 N · m

Fig. P4.165 and P4.166

4.166 For the curved bar and loading shown, determine the percent

error introduced in the computation of the maximum stress by

assuming that the bar is straight. Consider the case when (a) r

20 mm, (b) r

5 200 mm, (c) r

5 2 m.

4.167 The curved bar shown has a cross section of 30 3 30 mm. Knowing

that a 5 60 mm, determine the stress at (a) point A, (b) point B.

4.168 The curved bar shown has a cross section of 30 3 30 mm. Knowing

that the allowable compressive stress is 175 MPa, determine the

largest allowable distance a.

20 mm

30 mm

5 kN

Fig. P4.167 and P4.168

bee80288_ch04_220-313.indd Page 301 10/26/10 4:34:54 PM user-f499bee80288_ch04_220-313.indd Page 301 10/26/10 4:34:54 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

302

Pure Bending

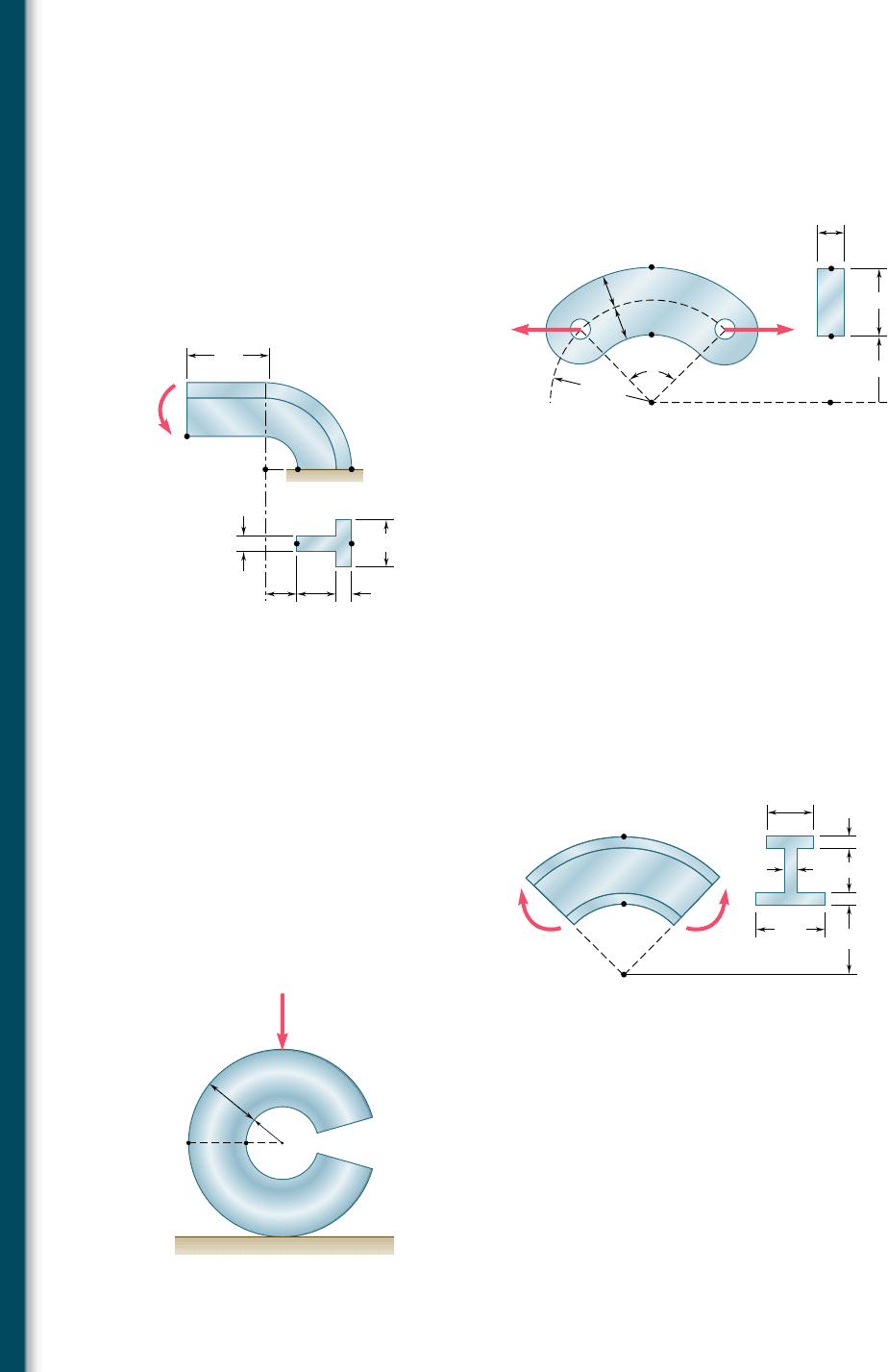
4.169 Steel links having the cross section shown are available with dif-

ferent central angles b. Knowing that the allowable stress is 12 ksi,

determine the largest force P that can be applied to a link for

which b 5 908.

0.4 in.

0.3 in.

0.8 in.

1.2 in.

P' P



Fig. P4.169

4.170 Solve Prob. 4.169, assuming that b 5 608.

4.171 A machine component has a T-shaped cross section that is orien-

tated as shown. Knowing that M 5 2.5 kN ? m, determine the

stress at (a) point A, (b) point B.

4.172 Assuming that the couple shown is replaced by a vertical 10-kN

force attached at point D and acting downward, determine the

stress at (a) point A, (b) point B.

4.173 Three plates are welded together to form the curved beam shown.

For the given loading, determine the distance e between the neu-

tral axis and the centroid of the cross section.

Dimensions in mm

100

5040 20

M 

2.5 kN · m

Fig. P4.171 and P4.172

2 in.

3 in.

0.5 in. 2 in.

3 in.

0.5 in.

Fig. P4.173 and P4.174

4.174 Three plates are welded together to form the curved beam shown.

For M 5 8 kip ? in., determine the stress at (a) point A, (b) point B,

4.175 The split ring shown has an inner radius r

5 20 mm and a circular

cross section of diameter d 5 32 mm. For the loading shown,

determine the stress at (a) point A, (b) point B.

4.176 The split ring shown has an inner radius r

5 16 mm and a circular

cross section of diameter d 5 32 mm. For the loading shown,

determine the stress at (a) point A, (b) point B.

2.5 kN

Fig. P4.175 and P4.176

bee80288_ch04_220-313.indd Page 302 11/11/10 3:03:21 PM user-f499bee80288_ch04_220-313.indd Page 302 11/11/10 3:03:21 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

303

Problems

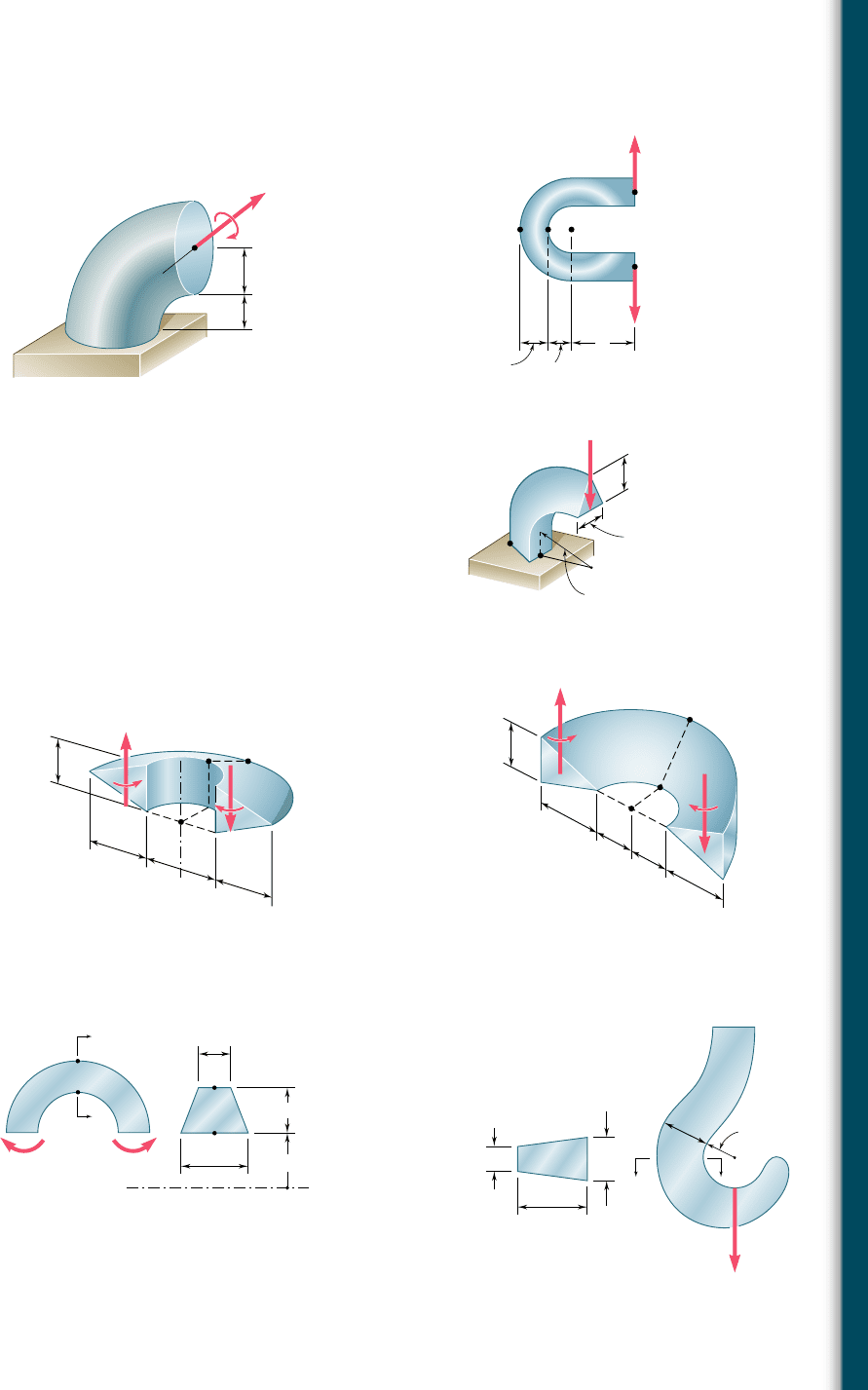
4.177 The curved bar shown has a circular cross section of 32-mm diameter.

Determine the largest couple M that can be applied to the bar about

a horizontal axis if the maximum stress is not to exceed 60 MPa.

16 mm

12 mm

Fig. P4.177

4.178 The bar shown has a circular cross section of 0.6 in.-diameter. Know-

ing that a 5 1.2 in., determine the stress at (a) point A, (b) point B.

4.179 The bar shown has a circular cross section of 0.6-in. diameter.

Knowing that the allowable stress is 8 ksi, determine the largest

permissible distance a from the line of action of the 50-lb forces

to the plane containing the center of curvature of the bar.

4.180 Knowing that P 5 10 kN, determine the stress at (a) point A,

(b) point B.

4.181 and 4.182 Knowing that M 5 5 kip ? in., determine the stress

at (a) point A, (b) point B.

50 lb

0.5 in.

0.6 in.

BAC

Fig. P4.178 and P4.179

90 mm

80 mm

100 mm

Fig. P4.180

4.183 For the curved beam and loading shown, determine the stress at

(a) point A, (b) point B.

2.5 in.

3 in.

2 in.

3 in.

Fig. P4.181

3 in.

2 in.

2.5 in.

Fig. P4.182

20 mm

30 mm

35 mm

40 mm

250 N · m

Section a-a

Fig. P4.183

35 mm

60 mm

25 mm

40 mm

60 mm

15 kN

Section a-a

Fig. P4.184

4.184 For the crane hook shown, determine the largest tensile stress in

section a-a.

bee80288_ch04_220-313.indd Page 303 11/11/10 3:03:21 PM user-f499bee80288_ch04_220-313.indd Page 303 11/11/10 3:03:21 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

304

Pure Bending

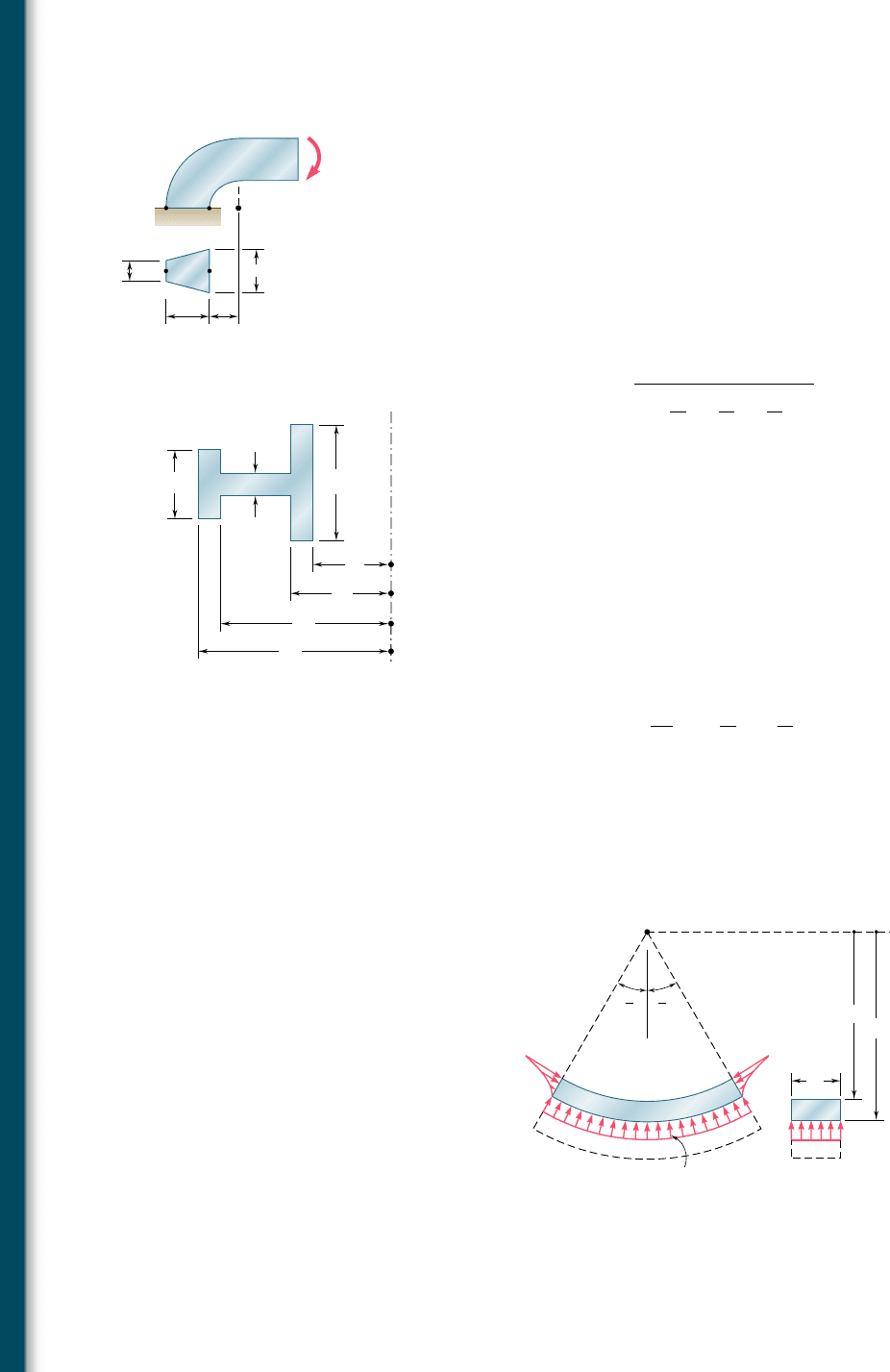
4.185 Knowing that the machine component shown has a trapezoidal

cross section with a 5 3.5 in. and b 5 2.5 in., determine the stress

at (a) point A, (b) point B.

4.186 Knowing that the machine component shown has a trapezoidal

cross section with a 5 2.5 in. and b 5 3.5 in., determine the stress

at (a) point A, (b) point B.

4.187 Show that if the cross section of a curved beam consists of two or

more rectangles, the radius R of the neutral surface can be

expressed as

R 5

where A is the total area of the cross section.

4.188 through 4.190 Using Eq. (4.66), derive the expression for R

given in Fig. 4.73 for

*4.188 A circular cross section.

4.189 A trapezoidal cross section.

4.190 A triangular cross section.

*4.191 For a curved bar of rectangular cross section subjected to a bend-

ing couple M, show that the radial stress at the neutral surface is

1 2

2 ln

and compute the value of s

for the curved bar of Examples 4.10

and 4.11.

(Hint: consider the free-body diagram of the portion of the beam

located above the neutral surface.)

6 in. 4 in.

80 kip · in.

Fig. P4.185 and P4.186

Fig. P4.187





Fig. P4.191

bee80288_ch04_220-313.indd Page 304 10/26/10 4:35:20 PM user-f499bee80288_ch04_220-313.indd Page 304 10/26/10 4:35:20 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

305

REVIEW AND SUMMARY

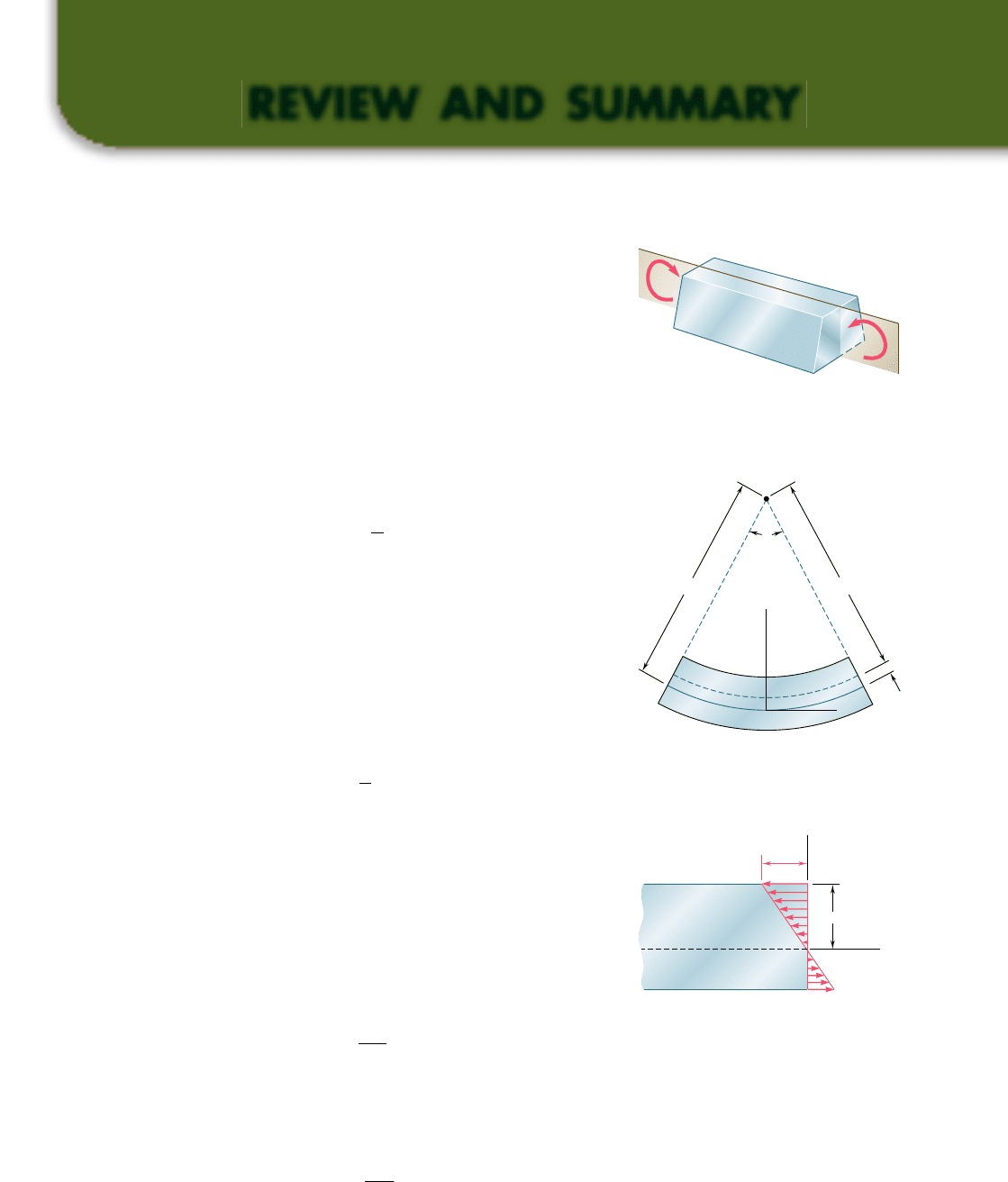
This chapter was devoted to the analysis of members in pure bend-

ing. That is, we considered the stresses and deformation in members

subjected to equal and opposite couples M and M9 acting in the

same longitudinal plane (Fig. 4.77).

We first studied members possessing a plane of symmetry and sub-

jected to couples acting in that plane. Considering possible deforma-

tions of the member, we proved that transverse sections remain plane

as a member is deformed [Sec. 4.3]. We then noted that a member

in pure bending has a neutral surface along which normal strains and

stresses are zero and that the longitudinal normal strain P

varies

linearly with the distance y from the neutral surface:

(4.8)

where r is the radius of curvature of the neutral surface (Fig. 4.78).

The intersection of the neutral surface with a transverse section is

known as the neutral axis of the section.

For members made of a material that follows Hooke’s law [Sec. 4.4],

we found that the normal stress s

varies linearly with the distance

from the neutral axis (Fig. 4.79). Denoting by s

the maximum

stress we wrote

(4.12)

where c is the largest distance from the neutral axis to a point in the

section.

By setting the sum of the elementary forces, s

dA, equal to zero, we

proved that the neutral axis passes through the centroid of the cross

section of a member in pure bending. Then by setting the sum of the

moments of the elementary forces equal to the bending moment, we

derived the elastic flexure formula for the maximum normal stress

(4.15)

where I is the moment of inertia of the cross section with respect to

the neutral axis. We also obtained the normal stress at any distance

y from the neutral axis:

(4.16)

Normal strain in bending

Normal stress in elastic range

Fig. 4.77

– y

A⬘

B⬘





Fig. 4.78



Neutral surface

Fig. 4.79

Elastic flexure formula

bee80288_ch04_220-313.indd Page 305 10/26/10 4:35:28 PM user-f499bee80288_ch04_220-313.indd Page 305 10/26/10 4:35:28 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

306

Pure Bending

Noting that I and c depend only on the geometry of the cross sec-

tion, we introduced the elastic section modulus

S 5

(4.17)

and then used the section modulus to write an alternative expression

for the maximum normal stress:

(4.18)

Recalling that the curvature of a member is the reciprocal of its

radius of curvature, we expressed the curvature of the member as

(4.21)

In Sec. 4.5, we completed our study of the bending of homogeneous

members possessing a plane of symmetry by noting that deforma-

tions occur in the plane of a transverse cross section and result in

anticlastic curvature of the members.

Next we considered the bending of members made of several materi-

als with different moduli of elasticity [Sec. 4.6]. While transverse

sections remain plane, we found that, in general, the neutral axis

does not pass through the centroid of the composite cross section

(Fig. 4.80). Using the ratio of the moduli of elasticity of the materials,

N. A.



– —









– —–







– —–





(a)(b)(c)

Fig. 4.80

N. A.



– —–



Fig. 4.81

we obtained a transformed section corresponding to an equivalent

member made entirely of one material. We then used the methods

previously developed to determine the stresses in this equivalent

homogeneous member (Fig. 4.81) and then again used the ratio of

the moduli of elasticity to determine the stresses in the composite

beam [Sample Probs. 4.3 and 4.4].

In Sec. 4.7, stress concentrations that occur in members in pure bend-

ing were discussed and charts giving stress-concentration factors for flat

bars with fillets and grooves were presented in Figs. 4.27 and 4.28.

Members made of several materials

Elastic section modulus

Curvature of member

Anticlastic curvature

Stress concentrations

bee80288_ch04_220-313.indd Page 306 11/11/10 3:03:22 PM user-f499bee80288_ch04_220-313.indd Page 306 11/11/10 3:03:22 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04